内生性和工具变量估计方法
二值选择模型内生性检验方法、步骤及Stata应用

二值选择模型内生性检验方法、步骤及Stata应用一、本文概述本文旨在深入探讨二值选择模型内生性检验的方法、步骤,并详细解析在统计软件Stata中的具体应用。
二值选择模型,作为一类重要的统计模型,广泛应用于经济学、社会学、医学等多个领域,用于分析二元结果数据的生成机制。
然而,在模型构建过程中,内生性问题往往不可避免,它可能导致模型估计结果的偏差,从而影响结论的准确性。
因此,对二值选择模型进行内生性检验,对于确保模型的有效性和可靠性至关重要。
本文首先将对二值选择模型内生性检验的理论基础进行梳理,包括内生性的定义、来源及其对模型估计的影响。
随后,将详细介绍几种常用的内生性检验方法,如Heckman两阶段选择模型、Probit模型的内生性检验等,并阐述各自的优缺点和适用场景。
在方法介绍的基础上,本文将重点阐述在Stata中进行二值选择模型内生性检验的具体步骤。
通过案例分析的方式,将展示如何在Stata 中实现各种内生性检验方法,包括数据的准备、模型的设定、命令的执行以及结果的解读等。
还将对Stata在处理内生性问题时的优势和局限性进行讨论。
本文将对二值选择模型内生性检验的未来发展进行展望,探讨新的检验方法和技术在解决内生性问题上的潜力和挑战。
通过本文的阐述,旨在为读者提供一套系统的二值选择模型内生性检验方法,并促进Stata在相关领域的应用和发展。
二、内生性检验的理论基础内生性问题是经济学、计量经济学和社会科学研究中一个普遍且重要的问题。
在二值选择模型中,内生性通常指的是模型中的解释变量与误差项之间存在相关性,这会导致估计结果产生偏差,从而影响到模型的预测和解释能力。
因此,对二值选择模型进行内生性检验至关重要。
内生性检验的理论基础主要建立在计量经济学的相关理论和假设之上。
在二值选择模型中,通常假设解释变量是外生的,即与误差项无关。
然而,在现实中,这一假设可能不成立。
例如,可能存在未观测到的遗漏变量,或者解释变量和误差项之间可能存在反向因果关系,这些都可能导致内生性问题。
IV和GMM相关估计步骤,内生性、异方差性等检验方法

IV和GMM相关估计步骤,内⽣性、异⽅差性…⼯具变量和⼴义矩估计相关步骤⼀、解释变量内⽣性检验⾸先检验解释变量内⽣性(解释变量内⽣性的Hausman 检验:使⽤⼯具变量法的前提是存在内⽣解释变量。
Hausman 检验的原假设为:所有解释变量均为外⽣变量,如果拒绝,则认为存在内⽣解释变量,要⽤IV;反之,如果接受,则认为不存在内⽣解释变量,应该使⽤OLS。
reg ldi lofdiest imat es st ore olsxt ivreg ldi (lofdi=l.lofdi ldep lexr)est imat es st ore ivhausman iv ols(在⾯板数据中使⽤⼯具变量,St at a提供了如下命令来执⾏2SLS:xt ivreg depvar [varlist1] (varlist_2=varlist_iv) (选择项可以为fe,re等,表示固定效应、随机效应等。
详⻅help xt ivreg)如果存在内⽣解释变量,则应该选⽤⼯具变量,⼯具变量个数不少于⽅程中内⽣解释变量的个数。
“恰好识别”时⽤2SLS。
2SLS的实质是把内⽣解释变量分成两部分,即由⼯具变量所造成的外⽣的变动部分,以及与扰动项相关的其他部分;然后,把被解释变量对中的这个外⽣部分进⾏回归,从⽽满⾜OLS前定变量的要求⽽得到⼀致估计量。
⼆、异⽅差与⾃相关检验在球型扰动项的假定下,2SLS是最有效的。
但如果扰动项存在异⽅差或⾃相关,⾯板异⽅差检验:xt gls enc invs exp imp esc mrl,igls panel(het)est imat es st ore het eroxt gls enc invs exp imp esc mrl,iglsest imat es st ore homolocal df = e(N_g) - 1lrt est het ero homo, df(`df')⾯板⾃相关:xt serial enc invs exp imp esc mrl则存在⼀种更有效的⽅法,即GMM。
证明工具变量估计法的渐进方程

一、概述工具变量估计法是一种在计量经济学中常用的方法,用于解决内生性问题。
内生性问题是指自变量与误差项之间存在相关性,这会导致普通最小二乘法(OLS)估计出现偏误,从而影响结果的准确性。
为了解决这一问题,研究者引入了工具变量估计法,其基本思想是利用外生的工具变量来代替内生的自变量,从而消除内生性。
二、工具变量估计法的基本模型1. 基本假设在介绍工具变量估计法的基本模型之前,我们首先来说明其基本假设。
工具变量估计法的基本假设包括两部分:(1)内生性假设:自变量与误差项之间存在相关性,即自变量不满足外生性假设。
(2)工具变量假设:工具变量与自变量相关,但与误差项不相关,即工具变量满足外生性假设。
2. 简单的工具变量模型工具变量估计法的基本模型可以表示为:Y = β1X + u (1)其中,Y 表示因变量,X 表示内生的自变量,β1 表示自变量 X 对因变量 Y 的影响。
由于 X 存在内生性问题,因此我们引入工具变量 Z 来代替 X,得到以下两个方程:X = γ1Z + v (2)Y = β2Z + e (3)其中,Z 表示外生的工具变量,γ1 和β2 分别表示 Z 对 X 和 Y 的影响,v 和 e 分别表示方程(2)和方程(3)的误差项。
根据方程(2)和方程(3),我们可以得到工具变量估计法的渐进方程。
三、工具变量估计法的渐进方程1. 渐进方程的基本形式工具变量估计法的渐进方程可以表示为:β2slim = [(∑zi*zi)^(-1) * (∑zi*yi)] / [(∑zi*zi)^(-1) * (∑zi*xi)] (4)其中,β2slim 表示工具变量估计法的渐进系数估计值,zi 表示工具变量,yi 和 xi 分别表示因变量和内生自变量的观测值。
2. 渐进方程的意义通过渐进方程(4)可以得到工具变量估计法的渐进系数估计值。
工具变量估计法的渐进方程引入了工具变量 Z,并利用 Z 来代替内生自变量 X,从而消除内生性问题。
内生性与工具变量估计方法
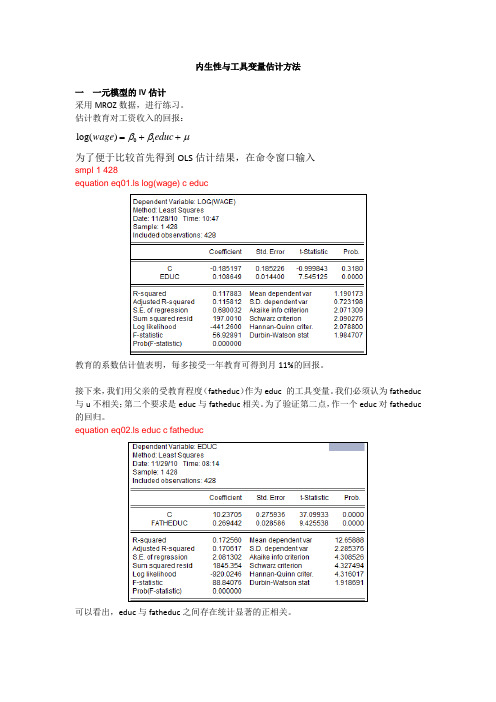
内生性与工具变量估计方法一 一元模型的IV 估计采用MROZ 数据,进行练习。
估计教育对工资收入的回报:01log()wage educ ββμ=++为了便于比较首先得到OLS 估计结果,在命令窗口输入smpl 1 428equation eq01.ls log(wage) c educ教育的系数估计值表明,每多接受一年教育可得到月11%的回报。
接下来,我们用父亲的受教育程度(fatheduc )作为educ 的工具变量。
我们必须认为fatheduc 与u 不相关;第二个要求是educ 与fatheduc 相关。
为了验证第二点,作一个educ 对fatheduc 的回归。
equation eq02.ls educ c fatheduc可以看出,educ 与fatheduc 之间存在统计显著的正相关。
采用fatheduc 作为educ 的工具变量,进行工具变量回归。
equation eq03.tsls log(wage) c educ @ fatheducIV 估计量的标准误是OLS 标准误的2.5倍,这在我们的意料之中。
二 多元模型的IV 估计 采用card 数据,进行练习。
估计教育对工资收入的回报:012log()var wage educ Control iables βββμ=+++为了便于对照,先做OLS 回归 Smpl 1 3010Equation eq01.ls log(wage) c educ exper expersq black smsa south smsa66 reg662 reg663 reg664 reg665 reg666 reg667 reg668 reg669在这个例子中,受教育程度的工具变量是标志着一个人是否在一所四年制大学附近成长的虚拟变量(nearc4)。
为了验证受教育程度与该虚拟变量的偏相关性,先做educ对nearc4以及其他所有外生变量的回归:Equation eq02.ls educ c nearc4 exper expersq black smsa south smsa66 reg662 reg663 reg664 reg665 reg666 reg667 reg668 reg669Nearc4的系数估计值意味着,在其他因素固定的情况下,曾住在大学附近的人所受的教育比不在大学附近长大的人平均多出约1/3年。
内生性和工具变量法

内生性和工具变量法从最根本的定义来说,内生外生首先是取决于系统的,在一个系统内部决定的变量,自然就是内生变量,在系统决定的变量,就是外生变量。
比如,给一个系统,比如地球,那么当前情况下地球上一切可以统计的变量都是内生变量,但是阳光就是外生变量。
那么如果以太阳系为研究的系统,那么自然,阳光此时也是内生变量了。
这样说内生性外生性似乎很容易理解,但是涉及到经济问题似乎不是那么好办了,因为经济系统中,所有的变量很难说是完全独立的,比如货币发行量,似乎是央行决定,按理说是外生的吧,但是慢着,央行的货币不是随便发的,也是因为有经济体有需求才会向社会发行货币,这个就是货币外生和货币内生的讨论,研究的文章有很多。
还是先说外生性吧,Leamer定义,如果y对x的条件分布(这个就是给出x 值,对应随机变量y)不随x的生成过程的修正而发生变化,那么x就是外生变量。
外生性似乎还是可以分为两类,前定性(前定变量是指独立于方程中同期和未来误差项的变量),严格外生(严格外生变量是指独立于方程中所有同期、未来,和过去误差项的变量)。
依照这个定义,我什么也看不出来,倒是可以从CLRM假定cov(Ut,Xt)≠0情况考虑。
既然cov(Ut,Xt)≠0可以叫成内生性,那么cov(Ut,Xt)=0大概可以叫外生变量了吧。
chris的书前面把这个假定强化为X是非随机变量,当显然这一假定是靠不住的,X更多情况下是随机变量。
这里涉及到前面曾经困惑的一个概率,随机解释变量,随机解释变量就是说解释变量是随机的,原因根据我的思考总结,大概是这两类,1.观测值存在误差2.根据Y=α+θX+μ,如果Y能影响X,由于Y是随机的,自然X也就带有随机性了。
随机解释变量容易带来内生性的问题,但却也不是必然,比如X是随机解释变量,但是X和u是独立的,也就是说cov(Ut,Xt)=0的时候,是不违背CLRM 假设的。
其实到这里,我们讨论的一切,什么内生性,自相关,异方差,这些为什么要讨论呢,就是因为我们经常用OLS模型进行估计,而CLRM的五个假定就是为了使得OLS的估计具有一致性,无偏性,有效性。
内生性与工具变量估计方法

内生性与工具变量估计方法一 一元模型的IV 估计采用MROZ 数据,进行练习。
估计教育对工资收入的回报:01log()wage educ ββμ=++为了便于比较首先得到OLS 估计结果,在命令窗口输入smpl 1 428equation eq01.ls log(wage) c educ教育的系数估计值表明,每多接受一年教育可得到月11%的回报。
接下来,我们用父亲的受教育程度(fatheduc )作为educ 的工具变量。
我们必须认为fatheduc 与u 不相关;第二个要求是educ 与fatheduc 相关。
为了验证第二点,作一个educ 对fatheduc 的回归。
equation eq02.ls educ c fatheduc可以看出,educ 与fatheduc 之间存在统计显著的正相关。
采用fatheduc 作为educ 的工具变量,进行工具变量回归。
equation eq03.tsls log(wage) c educ @ fatheducIV 估计量的标准误是OLS 标准误的2.5倍,这在我们的意料之中。
二 多元模型的IV 估计 采用card 数据,进行练习。
估计教育对工资收入的回报:012log()var wage educ Control iables βββμ=+++为了便于对照,先做OLS 回归 Smpl 1 3010Equation eq01.ls log(wage) c educ exper expersq black smsa south smsa66 reg662 reg663 reg664 reg665 reg666 reg667 reg668 reg669在这个例子中,受教育程度的工具变量是标志着一个人是否在一所四年制大学附近成长的虚拟变量(nearc4)。
为了验证受教育程度与该虚拟变量的偏相关性,先做educ对nearc4以及其他所有外生变量的回归:Equation eq02.ls educ c nearc4 exper expersq black smsa south smsa66 reg662 reg663 reg664 reg665 reg666 reg667 reg668 reg669Nearc4的系数估计值意味着,在其他因素固定的情况下,曾住在大学附近的人所受的教育比不在大学附近长大的人平均多出约1/3年。
2sls工具变量法

2sls工具变量法2SLS工具变量法是一种常用的计量经济学方法,用于解决内生性问题。
本文将介绍2SLS工具变量法的基本原理、应用场景以及优缺点。
一、2SLS工具变量法的基本原理2SLS全称为Two-Stage Least Squares,即两阶段最小二乘法。
它主要应用于当存在内生性问题时,通过引入工具变量来解决内生性问题。
内生性问题指的是自变量与误差项之间存在相关性,导致OLS估计结果偏误。
2SLS工具变量法的基本原理是通过两个阶段的回归来解决内生性问题。
第一阶段,使用工具变量对内生变量进行回归得到预测值;第二阶段,将预测值作为自变量,与因变量进行回归得到最终估计结果。
二、2SLS工具变量法的应用场景2SLS工具变量法适用于存在内生性问题的经济学研究。
常见的应用场景有以下几种:1. 自变量的测量误差:当自变量存在测量误差时,可以使用与自变量高度相关但与误差项不相关的工具变量进行修正。
2. 隐藏变量:当存在未观测到但影响自变量的隐藏变量时,可以使用与隐藏变量相关但与误差项不相关的工具变量进行估计。
3. 同时方程系统:当存在同时方程系统时,通过引入工具变量来解决内生性问题。
三、2SLS工具变量法的优缺点2SLS工具变量法的优点在于可以通过引入工具变量来解决内生性问题,得到无偏的估计结果。
同时,由于2SLS方法是基于回归的,因此可以利用回归分析的相关性、显著性等统计检验方法来评估模型的拟合程度和推断。
然而,2SLS工具变量法也存在一些缺点。
首先,工具变量的选择是关键,如果选择不当可能会引入其他问题,如工具变量无效性等。
其次,2SLS方法可能会损失一部分样本,导致样本量减小。
此外,2SLS方法要求模型的误差项符合一定的假设条件,如无异方差性、正态分布等,否则估计结果可能失效。
四、总结2SLS工具变量法是一种解决内生性问题的常用方法。
通过引入与内生变量相关但与误差项不相关的工具变量,可以得到无偏的估计结果。
logit模型的工具变量法

logit模型的工具变量法1. 引言logit模型是一种广泛应用于经济学和社会科学领域的统计模型,用于研究二分类问题。
在实际应用中,我们常常面临内生性问题,即解释变量与误差项之间存在相关性。
为了解决内生性问题,研究者引入了工具变量法。
本文将详细介绍logit模型的工具变量法,包括定义、原理、估计方法以及应用案例等。
2. logit模型简介logit模型是一种广义线性模型,用于研究二分类问题。
其基本形式为:P(Y=1|X)=11+e−Xβ其中,P(Y=1|X)表示因变量Y取值为1的概率,X为解释变量,β为参数向量。
logit模型的核心思想是通过一个线性组合的函数将解释变量映射到一个概率值,从而进行分类预测或推断。
3. 内生性问题与工具变量法在实际应用中,解释变量与误差项之间往往存在相关性,即内生性问题。
内生性问题会导致参数估计的偏误和不一致性,从而影响模型的准确性和可靠性。
为了解决内生性问题,研究者引入了工具变量法。
3.1 内生性问题的原因内生性问题通常由以下原因引起:•遗漏变量:模型中未包含影响解释变量和因变量的未观测因素。
•测量误差:解释变量和因变量的测量误差导致相关性。
•同时方程偏误:解释变量和因变量之间存在双向因果关系。
3.2 工具变量法的原理工具变量法通过引入一个或多个与内生解释变量相关但与误差项不相关的工具变量,来解决内生性问题。
工具变量需要满足两个条件:•相关性:工具变量与内生解释变量之间存在相关性。
•排除性:工具变量与误差项之间不存在相关性。
工具变量法的基本思路是利用工具变量与内生解释变量之间的相关性,通过两阶段最小二乘法估计模型参数。
在第一阶段,利用工具变量估计内生解释变量的无条件期望值。
在第二阶段,将无条件期望值代入原模型进行估计。
4. 工具变量法的估计方法工具变量法的估计方法主要包括两阶段最小二乘法(Two-stage Least Squares,2SLS)和广义矩估计法(Generalized Method of Moments, GMM)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.1 内生性
6.1.1 OLS估计的不一致性
以不带截距项的二元回归模型为例:
Y 1 X1 X 2 u
Cov( X1, u) 0 Cov( X 2 , u) 0
2 2 2 ˆ S S S X1 , X 2 X1 ,u ˆ X1 X 2 ,u 2 2 2 ˆX S X1 S X 2 (1 ) 1,X 2
2 ˆ u i1 i n
1 其中, ˆ2 ˆZ ,X
n2
n
n
i 1
( X i X )(Z i Z )
i1 ( X i X )2
2 ( Z Z ) i i 1
n
ˆ ˆ X ˆi Yi u 0 IV 1IV i
工具变量估计法
一元线性回归模型
6.1 内生性
6.1.2 内生性产生的原因
模型设定错误、测量误差和联立性
• 模型设定错误是导致内生性最常见的原因,模型 设定错误往往表现为相关变量的缺失,缺失变量 成为错误设定模型误差项的一部分,当缺失变量 和模型中其他变量相关时,就会导致这些变量的 内生性。(工资与教育、能力)、 • 不相干变量引入不会影响参数估计的无偏性和一 致性,但是会影响参数估计的有效性。
6.1 内生性
6.1.1 OLS估计的不一致性
2 1 2 SX n ( X X ) , ji j j i 1 n n
j 1,2
2 1 SX n i1 ( X ji X j )ui , j 1,2 j ,u 2 1 SX n i1 ( X 1i X 1 )( X 2i X 2 ) 1,X 2 n
6.2 工具变量估计方法
6.2.1 工具变量估计法 6.2.2 两阶段最小二乘法:TSLS
6.2 工具变量估计方法
6.2.1 工具变量估计法
工具变量估计法
一元线性回归模型
Y 0 1 X u
定义1:如果存在变量 Z ,满足 (1)与 u 不相关 Cov( Z , u ) 0 (2)与 X 相关 Cov(Z , X ) 0 称 Z 为 X 的工具变量,也称工具(instrument)。
第6 章
内生性和工具变量估计方法
内生性和工具变量估计方法
6.1 内生性
6.1.1 OLS估计的不一致性 6.1.2 内生性产生的原因
6.2 工具变量估计方法
6.2.1 工具变量估计法 6.2.2 两阶段最小二乘法:TSLS
6.3 内生性检验 重要概念
6.1 内生性
6.1.1 OLS估计的不一致性 6.1.2 内生性产生的原因
Y 0 1 X u
假设检验: 统计量
t 1
ˆ 1IV S1IV
给定误差项服从正态分布,则 t1 ~ t (n 2) 若没给定分布,大样本情况下服从标准正态分布。
工具变量估计法
1
(Y
i 1
i
工具变量估计法
一元线性回归模型
Y 0 1 X u
ˆ Y ˆ 0 IV 1IV ˆ 1IV
Байду номын сангаас
n
i 1 n
( Z i Z )(Yi Y )
i 1
( Z i Z )( X i X )
工具变量估计法
一元线性回归模型
Y 0 1 X u
1 ˆ 1 1 in
n
( X i X )ui
2
i1 ( X i X )
n
1
n 1
n
i 1 n
Cov(X,u) 0 2 Var( X ) (Xi X ) i 1
( X i X )ui
• 多元线性模型下,不仅内生变量前的回归 系数不一致,外生变量前的系数也可能不 一致。
6.1 内生性
6.1.1 OLS估计的不一致性
模型: Y 0 1 X1 2 X 2 k X k u 若 Cov( X r , u) 0 则 X r 为内生自变量。 • 存在内生自变量时,OLS估计不再有一致性
6.1 内生性
6.1.1 OLS估计的不一致性
以一元回归模型为例: Y 0 1 X u
2 X Cov ( X 2 , u ) X , X Cov ( X 1 , u ) ˆ 2 2 2 [ X X (1 X , X )]
1 2 1
ˆ 不以概率收敛到 。 只要 X , X 0 , 2 2
1 2
1
2
1
2
6.1 内生性
6.1.1 OLS估计的不一致性
工具变量估计法
一元线性回归模型
Y 0 1 X u
总体矩条件:
Cov(Z,u) E (Zu) E[(Y 0 1 X )Z ] 0 E(u) E(Y 0 1 X ) 0
类比出样本矩条件:
n n
1
(Y
i 1 n
n
i
ˆ ˆ X )Z 0 0 1 i i ˆ ˆ X )0 0 1 i
结论2:工具变量估计的性质 (1)工具变量估计是一致估计 (2)工具变量估计具有渐进正态分布
Z
X
Y
u
工具变量估计法
一元线性回归模型
Y 0 1 X u
结论3:OLS估计和工具变量估计 一元线性回归模型的自变量为外生时,OLS估 计可看做以自变量本身为工具的工具变量估计。 例子6.1 气温与冷饮消费(续)
用住房面积 House 作为工具变量
Coldr 0 1AirCd u
工具变量估计法
一元线性回归模型
Y 0 1 X u
方差估计:若 Var (u | Z ) E(u 2 | Z ) 2
S2 1 IV ˆ2 n 2 2 ˆ Z ,X ( X X ) i1 i
结论1:OLS估计的不一致性 (1)线性回归模型内生自变量回归系数的 OLS估计不是一致估计; (2)如果和内生自变量相关,外生自变量回 归系数的OLS估计不是一致估计
6.1 内生性
6.1.1 OLS估计的不一致性
内生性影响图示:
X
Y
u
dY / dX du / dX
ˆ 是对 du / dX 的估计。
