点乘与叉乘
点乘叉乘行列式

点乘叉乘行列式点乘、叉乘和行列式是线性代数中常见的运算,它们在解决向量、平面和空间中的问题时起到了重要的作用。
本文将探讨点乘、叉乘和行列式的定义、性质和应用。
一、点乘(内积)点乘是向量运算中的一种,也称为内积。
给定两个n维向量a和b,它们的点乘表示为a·b,其结果是一个标量。
点乘的计算方法是将两个向量对应位置的分量相乘,然后将结果相加。
例如,对于二维向量a=(a1, a2)和b=(b1, b2),它们的点乘为a·b=a1b1+a2b2。
点乘具有以下性质:1. 交换律:a·b=b·a。
即点乘的结果与向量的顺序无关。
2. 分配律:a·(b+c)=a·b+a·c。
即点乘对向量的加法满足分配律。
3. 数乘结合律:(k·a)·b=k·(a·b)=a·(k·b)。
即点乘对数乘满足结合律。
点乘在几何上有重要的应用。
首先,两个向量的点乘可以用来计算它们之间的夹角。
根据定义,两个向量a和b的夹角θ满足cosθ=(a·b)/(|a||b|),其中|a|和|b|分别表示向量a和b的模。
其次,点乘还可以用来判断两个向量是否垂直。
当且仅当a·b=0时,向量a和b垂直。
二、叉乘(外积)叉乘是向量运算中的一种,也称为外积。
给定两个三维向量a和b,它们的叉乘表示为a×b,其结果是一个新的向量。
叉乘的计算方法是利用行列式的形式进行计算。
例如,对于三维向量a=(a1, a2, a3)和b=(b1, b2, b3),它们的叉乘为a×b=(a2b3-a3b2, a3b1-a1b3, a1b2-a2b1)。
叉乘具有以下性质:1. 反交换律:a×b=-(b×a)。
即叉乘的结果与向量的顺序有关,且方向相反。
2. 分配律:a×(b+c)=a×b+a×c。
矢量点乘和叉乘

矢量点乘和叉乘
矢量点乘和叉乘是向量运算中常见的两种运算。
简单来说,点乘是一种运算,它将两个向量相乘并得到一个标量;而叉乘是另一种运算,它将两个向量相乘并得到一个新的向量。
具体来说,对于两个向量a和b,它们的点乘可以表示为a·b,结果为一个标量。
点乘的计算公式为:
a·b = |a||b|cosθ
其中,|a|和|b|分别表示两个向量的模长,θ表示它们之间的夹角。
可以看出,点乘的结果是两个向量在同一方向上的投影的乘积。
另一方面,a和b的叉乘可以表示为a×b,结果为一个新的向量。
叉乘的计算公式为:
a×b = |a||b|sinθn
其中,|a|和|b|分别表示两个向量的模长,θ表示它们之间的夹角,n表示垂直于a和b所在平面的单位向量。
可以看出,叉乘的结果是一个新的向量,它的方向垂直于a和b所在平面,并且大小等于两个向量所围成的平行四边形的面积。
总之,矢量点乘和叉乘是两个基本的向量运算,它们在物理、工程、计算机图形学等领域中广泛应用。
点乘和叉乘函数

点乘和叉乘函数全文共四篇示例,供读者参考第一篇示例:点乘和叉乘是向量运算中常用的两种乘法运算,它们在向量代数中有着重要的作用。
在数学、物理学、工程学等领域,点乘和叉乘被广泛应用于各种问题的求解。
本文将介绍点乘和叉乘的定义、性质和在实际应用中的一些例子。
一、点乘函数在向量代数中,点乘也称为数量积或内积,是两个向量相乘后的结果。
点乘的定义如下:设有两个三维向量a=(a1,a2,a3)和b=(b1,b2,b3),它们的点乘结果为:a•b=a1b1+a2b2+a3b3从点乘的定义可以看出,点乘的结果是一个标量(即一个实数),它表示两个向量的相似程度。
如果点乘的结果为正数,说明两个向量的夹角小于90度;如果点乘的结果为负数,说明两个向量的夹角大于90度;如果点乘的结果为零,说明两个向量垂直。
点乘还有一种几何解释,即两个向量在某一个方向上的投影乘积之和。
点乘的性质包括交换律和分配律。
交换律即a•b=b•a,分配律即(a+b)•c=a•c+b•c。
这些性质使得点乘在向量运算中具有很好的性质,方便我们进行计算。
点乘在实际应用中有很多用途,比如计算两个向量之间的夹角、计算向量的模长、判断向量的正交性等。
在物理学中,点乘常用于求解力的功率,电场和电势之间的关系等问题。
从叉乘的定义可以看出,叉乘的结果是一个新的向量,它垂直于原来两个向量所构成的平面。
叉乘还有一个几何解释,即结果向量的模长等于原来两个向量所构成的平行四边形的面积。
总结点乘和叉乘是向量运算中常用的两种乘法运算,它们在向量代数中有着重要的应用。
点乘是两个向量相乘后的结果,是一个标量;叉乘是两个向量相乘后的结果,是一个新的向量。
它们都具有很好的性质,方便我们进行计算。
第二篇示例:点乘和叉乘是在向量和矩阵运算中经常用到的两种重要运算。
点乘也叫数量积或内积,叉乘又叫向量积或外积。
它们在几何、物理、计算机图形学等领域都有着广泛的应用。
本文将详细介绍点乘和叉乘的定义、性质及其在实际问题中的应用。
向量点乘和叉乘的意义

向量点乘和叉乘的意义
1、向量点乘意义:可以用来表征或计算两个向量之间的夹角,以及在b向量在a向量方向上的投影。
2、向量叉乘意义:在三维几何中,向量a和向量b的叉乘结果是一个向量,更为熟知的叫法是法向量,该向量垂直于a和b向量构成的平面。
在3D图像学中,叉乘的概念非常有用,可以通过两个向量的叉乘,生成第三个垂直于a,b的法向量,从而构建X、Y、Z坐标系。
3、两者区别:
(1)向量点乘结果是标量,是两个向量在一个方向的累计结果,结果只保留大小属性,抹去方向属性,就相等于降维;
(2)向量叉乘,是这这两个向量平面上,垂直生成新的向量,大小是两个向量构成四边形的面积。
相等于生维。
这是运算所需要,向量加和减都是在同一纬空间操作的,如果要想实现维度的变化就要在向量的乘法做出定义。
点乘和叉乘函数-概述说明以及解释

点乘和叉乘函数-概述说明以及解释1.引言文章1.1 概述部分的内容是对点乘和叉乘函数的整体概括和简要介绍。
可以参考如下内容:概述:点乘函数和叉乘函数是向量运算中常见的数学工具,它们在多个领域中都具有重要的应用价值。
点乘函数和叉乘函数可以用来计算向量之间的关系,求取它们的数量积和向量积。
点乘函数:点乘函数,也被称为数量积或内积,是两个向量的一种运算方法。
通过点乘函数,我们可以求得两个向量之间的夹角、判断它们是否垂直、计算它们在某一方向上的投影等。
点乘函数的定义和原理是基于向量的长度和夹角的数学性质。
叉乘函数:叉乘函数,也被称为向量积或外积,是两个向量的另一种运算方法。
通过叉乘函数,我们可以求得两个向量所在平面的法向量、计算它们构成的平行四边形的面积等。
叉乘函数的定义和原理是基于向量的长度和夹角的几何性质。
点乘和叉乘函数的区别与联系:尽管点乘函数和叉乘函数是两个不同的运算方法,但它们之间存在一些联系和关联。
点乘函数和叉乘函数都是向量运算的重要工具,它们在不同领域中都具有广泛的应用。
点乘函数主要用于计算相似性和判断方向关系,而叉乘函数主要用于计算垂直性和求取平面上的向量。
本文将详细介绍点乘函数和叉乘函数的定义、原理、用途和应用。
同时,还将探讨点乘函数和叉乘函数之间的区别与联系,包括它们的数学性质和关系。
最后,我们将总结点乘函数和叉乘函数的重要性和作用,并对它们的未来发展进行展望。
在文章的结论部分,我们将给出相应的结论和建议,以期能够更好地理解和应用点乘和叉乘函数。
1.2 文章结构本文将围绕点乘和叉乘函数展开讨论,文章结构如下:引言部分将对点乘和叉乘函数进行概述,并介绍全文的目的和结构。
正文部分将主要分为三个小节:点乘函数、叉乘函数和点乘与叉乘函数的区别与联系。
2.1 点乘函数部分将详细介绍其定义和原理,并探讨其在不同领域的应用和使用场景。
同时,通过一些具体的示例和案例,解释点乘函数在实际问题中的作用和意义。
向量点乘与叉乘的概念及几何意义
向量点乘:(内积)点乘(Dot Product)的结果是点积,又称数量积或标量积(Scalar Product)。
在空间中有两个向量: \vec a=(x_1,y_1,z_1) , \vecb=(x_2,y_2,z_2), \vec a 与 \vec b之间夹角为 \theta。
从代数角度看,点积是对两个向量对应位置上的值相乘再相加的操作,其结果即为点积。
\vec a\cdot \vecb=x_1x_2+y_1y_2+z_1z_2从几何角度看,点积是两个向量的长度与它们夹角余弦的积。
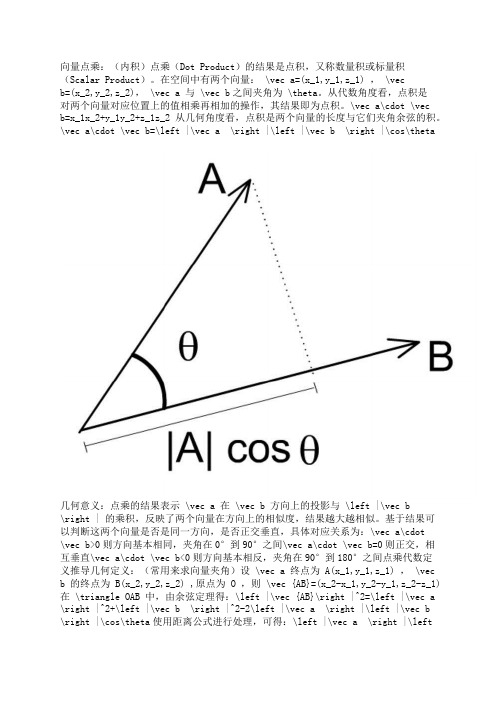
\vec a\cdot \vec b=\left |\vec a \right |\left |\vec b \right |\cos\theta几何意义:点乘的结果表示 \vec a 在 \vec b 方向上的投影与 \left |\vec b\right | 的乘积,反映了两个向量在方向上的相似度,结果越大越相似。
基于结果可以判断这两个向量是否是同一方向,是否正交垂直,具体对应关系为:\vec a\cdot\vec b>0则方向基本相同,夹角在0°到90°之间\vec a\cdot \vec b=0则正交,相互垂直\vec a\cdot \vec b<0则方向基本相反,夹角在90°到180°之间点乘代数定义推导几何定义:(常用来求向量夹角)设 \vec a 终点为 A(x_1,y_1,z_1) , \vec b 的终点为B(x_2,y_2,z_2) ,原点为 O ,则 \vec {AB}=(x_2-x_1,y_2-y_1,z_2-z_1)在 \triangle OAB 中,由余弦定理得:\left |\vec {AB}\right |^2=\left |\vec a \right |^2+\left |\vec b \right |^2-2\left |\vec a \right |\left |\vec b \right |\cos\theta使用距离公式进行处理,可得:\left |\vec a \right |\left|\vec b \right |\cos\theta=\frac {x_1^2+y_1^2+z_1^2+x_2^2+y_2^2+z_2^2-[(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2]}{2}去括号后合并,可得:\left |\vec a \right |\left |\vec b \right |\cos\theta=x_1x_2+y_1y_2+z_1z_2=\vec a\cdot \vec b根据上面的工式可计算 \vec a 与 \vec b 之间的夹角: \theta=\arccos (\frac {\vec a\cdot\vec b} {\left |\vec a \right |\left |\vec b \right |})向量叉乘:(外积)叉乘(Cross Product)又称向量积(Vector Product)。
向量点乘和叉乘运算法则

向量点乘和叉乘运算法则
向量点乘和叉乘是向量运算中常用的两种运算法则。
向量点乘也叫内积,是两个向量的数量积,结果是一个标量。
向量点乘的计算公式是:a·b=|a|·|b|·cosθ,其中a和b是两个向量,θ是它们的夹角。
向量点乘的结果有以下几个特点:当θ=0时,结果最大,为|a|·|b|;当θ=90°时,结果为0,表示两个向量垂直;当θ=180°时,结果最小,为-|a|·|b|。
向量叉乘也叫外积,是两个向量的向量积,结果是一个向量。
向量叉乘的计算公式是:a×b=|a|·|b|·sinθ·n,其中n是垂直于a和b的法向量,θ是它们的夹角。
向量叉乘的结果有以下几个特点:它的方向垂直于a和b确定的平面,且满足右手定则;当θ=0或θ=180°时,结果为0,表示两个向量共线;当θ=90°时,结果最大,为|a|·|b|。
向量点乘和叉乘在物理、工程等领域广泛应用,例如计算力矩、功率、电场强度等。
在计算机图形学领域,向量点乘和叉乘常用于计算三维空间中的相交、平面方程等问题。
掌握向量点乘和叉乘的运算法则,对于理解和应用向量运算具有重要意义。
- 1 -。
向量点乘和叉乘运算法则

向量点乘和叉乘是向量运算中常见的两种运算法则。
它们在物理学、工程学和计算机图形学中得到广泛应用,用于描述向量之间的关系和进行向量运算。
向量点乘运算法则,也被称为内积或数量积,是指两个向量之间的乘积。
设有两个三维向量A和B,它们分别表示为:A = (A₁, A₂, A₃)B = (B₁, B₂, B₃)两个向量的点乘运算可以记作A·B,计算公式为:A·B = A₁B₁ + A₂B₂ + A₃B₃点乘运算的结果为一个标量,表示两个向量之间的相似度。
点乘运算有以下几个性质:1.交换律:A·B = B·A。
即两个向量的点乘运算结果与向量的顺序无关。
2.结合律:(A·B)·C = A·(B·C)。
即点乘运算满足结合律。
3.分配律:A·(B+C) = A·B + A·C。
即点乘运算与向量的加法满足分配律。
点乘运算可以判断两个向量之间的夹角关系。
设夹角为θ,则点乘运算可以表示为:A·B = |A||B|cosθ其中|A|和|B|分别表示向量A和B的模,θ表示向量A和B之间的夹角。
根据点乘运算的结果,可以判断夹角的大小、方向和两向量之间的正交性。
向量叉乘运算法则,也称为外积或向量积,是指两个向量之间的乘积。
设有两个三维向量A和B,它们分别表示为:A = (A₁, A₂, A₃)B = (B₁, B₂, B₃)两个向量的叉乘运算可以记作A×B,计算公式为:A×B = (A₂B₃ - A₃B₂, A₃B₁ - A₁B₃, A₁B₂ - A₂B₁)叉乘运算的结果为一个向量,其方向垂直于参与运算的两个向量,并遵循右手法则。
叉乘运算有以下几个性质:1.反交换律:A×B = -B×A。
即叉乘运算不满足交换律。
2.结合律:(A×B)×C = A×(B×C)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点乘
目录
点乘
叉乘
点乘
点乘(dot product),也叫向量的内积、数量积。
顾名思义,求下来的结果是一个数。
向量a·向量b=|a||b|cos<a,b> ( <a,b> 指向量a与向量b之间的夹角)
在物理学中,已知力与位移求功,实际上就是求向量F与向量s的内积,即要用点乘。
坐标化表示
将向量用坐标表示(三维向量),
若向量a=(a1,b1,c1),向量b=(a2,b2,c2),
则,向量a·向量b=a1a2+b1b2+c1c2
运用
(一)点乘可用于判断向量垂直
判断条件:
在向量a与向量b的模皆不为0的情况下,向量a·向量b=0
由向量a·向量b=|a||b|cos<a,b>可很容易的得出
当|a| 、|b|皆不为0时,cos<a,b>为0
也即向量a与向量b互相垂直。
(二)关于用点乘判断向量平行的误区
判断平行:
向量a·向量b=|a|*|b|;
而非向量a·向量b=1(×)
由向量a·向量b=|a||b|cos<a,b>可很容易的得出
叉乘
叉乘(cross product),也叫向量的外积、向量积。
顾名思义,求下来的结果是一个向量,记这个向量为c。
|向量c|=|向量a×向量b|=|a||b|sin<a,b> ( <a,b> 指向量a与向量b之间的夹角)
向量c的方向与a,b所在的平面垂直,且方向要用“右手法则”判断(用右手的食指先表示向量a的方向,然后中指朝着手心的方向摆动到向量b的方向,大拇指所指的方向就是向量c的方向)。
因此
向量的外积不遵守乘法交换率,因为向量a×向量b= - 向量b×向量a
在物理学中,已知力与力臂求力矩,就是向量的外积,即叉乘。
坐标化表示
将向量用坐标表示(三维向量),
若向量a=(a1,b1,c1),向量b=(a2,b2,c2),
则,向量a×向量b= | i j k ||a1 b1 c1||a2 b2 c2|
=(b1c2-b2c1,c1a2-a1c2,a1b2-a2b1)
(i、j、k分别为空间中相互垂直的三条坐标轴的单位向量)。
