北师大版高中数学选修2-2第二章章末总结
北师大版高中数学选修2-2 本章小结建议

选修2-2 本章小结建议第一章推理与证明一、学习要求1.合情推理的意义与应用(1)会利用归纳进行简单的推理与猜想;(2)会利用类比进行简单的推理与猜想。
2.演绎推理的意义与应用(1)体会演绎推理的重要性,并能进行简单的推理;(2)了解数学证明的几种基本方法:综合法、分析法、反证法,并能运用这些方法进行一些简单的数学证明;(3)了解合情推理和演绎推理之间的联系、差异和各自所起的作用。
二、复习建议1.依据课本、笔记及作业总结本章的基本知识,掌握本章的基本思想方法,使知识有条理、有层次地呈现。
2.按照学习要求中的两个部分,做出本章小结。
3.本章复习时,可供参考的思考问题:(1)日常和数学学习中有哪些合情推理的方式?举例说明;(2)如何运用合情推理进行数学和其他学科的学习?如何避免合情推理的局限性?(3)分析法与综合法各自有何特点?在解决问题时各自有何作用?(4)归纳推理与数学归纳法有何关系?(选修1-2无)(5)与其它证明方法相比,反证法的思考过程有何特点?4.请同学们相互交流学习本章的感受,特别是本章所学的常用的思维方式在日常学习和生活中的应用。
第二章变化率与导数一、学习要求1.导数的概念通过具体情境,感受在现实世界和生活实际中存在着大量的变化率问题,体会平均变化率和导数的实际意义,理解导数的几何意义。
2.导数运算(1)会利用导数定义计算一些简单的函数的导数。
(2)会利用导数公式表求出给定函数的导数。
(3)掌握求导的四则运算法则,并会利用导数的四则运算法则求出函数的导函数。
(4)了解简单复合函数的求导法则,并会利用导数公式表求出一些简单的复合函数的导数。
二、复习建议1.依据课本、笔记及作业总结本章的基本知识,掌握本章的基本思想方法,使知识有条理、有层次地呈现。
2.按照学习要求中的两个部分,以适当形式做出本章小结。
3.本章复习时,可供参考的思考问题:(1)实际生活中经常会涉及变化快慢的问题,你是否有体会?(2)什么是导数?如何利用定义求函数的导数?怎样解释导数的实际意义?能否举例说明?(3)是否会用导数的四则运算法则求函数的导数?(4)复合函数的中间变量的意义是什么?如何寻找中间变量?怎样求复合函数的导数?4.请同学们相互交流学习本章的感受与体会。
北师大版数学选修1-2 第二章 框图 章末归纳总结(40张)

的不同,都会使画出的结构图发生变化.
第二章 章末归纳总结
成才之路 ·高中新课程 ·学习指导 ·北师大版 ·数学 ·选修1-2
如图是向量运算的知识结构图,如果要加入“向量共线的
充要条件”,则应该是在________的下位.
[答案] 数乘
[解析] 式.
第二章 章末归纳总结
向量共线的充要条件是两个向量能写成数乘的形
第二章
章末归纳总结
成才之路 ·高中新课程 ·学习指导 ·北师大版 ·数学 ·选修1-2
阅读下面的程序框图,若输出的 n是100,则S和T的值分别是( A.2550,2500 B.2550,2550 C.2500,2500 )
D.2500,2550
[答案] A [解析] 从程序框图的运算特点,可以发现:S=100+98
第二章
章末归纳总结
成才之路 ·高中新课程 ·学习指导 ·北师大版 ·数学 ·选修1-2
4 .阅读如图所示的小流域综合治理结构图,并对其进行
解释.
第二章
章末归纳总结
成才之路 ·高中新课程 ·学习指导 ·北师大版 ·数学 ·选修1-2
[解析]
小流域综合治理可以有3个措施:工程措施、生物
措施和农业技术措施.其中,工程措施包括打坝建库、平整土 地、修基本农田和引水灌溉,其功能是贮水拦沙、改善生产条 件和合理利用水土;生物措施包括栽种乔木、灌木和草木,其 功能是蓄水保土和发展多种经营;农业技术措施包括深耕改 土、科学施肥、选育良种、地膜覆盖和轮作套种,其功能是蓄 水保土、提高肥力和充分利用光热.
第二章
章末归纳总结
成才之路 ·高中新课程 ·学习指导 ·北师大版 ·数学 ·选修1-2
(3)按其逻辑顺序将它们排列起来,并用线相连.
2015年秋北师大版数学选修2-2课件 第2章 变化率与导数 §2

第二章
§2
成才之路 ·高中新课程 ·学习指导 · 北师大版 ·数学 ·选修2-2
导数 有定义 1.定义:y=f(x)在x0点附近 __________,对自变量的任一
Δy 改变量Δx,函数改变量为Δy=f(x0+Δx)-f(x0),若极限 lim Δx Δx→0 fx0+Δx-fx0 lim Δx =_____________________ 存在 ,称该极限值为f(x)在x0点的导 Δx→0 ..
第二章
§2
成才之路 ·高中新课程 ·学习指导 · 北师大版 ·数学 ·选修2-2
π 5.曲线y=f(x)在点(x0,f(x0))处的切线的倾斜角为 4 ,则 f′(x0)=________.
[答案] 1
[ 解析] π f′(x0)=tan4=1.
第二章
§2
成才之路 ·高中新课程 ·学习指导 · 北师大版 ·数学 ·选修2-2
第二章
§2
成才之路 ·高中新课程 ·学习指导 · 北师大版 ·数学 ·选修2-2
2.导数的几何意义 如图所示,设函数y=f(x)的图像 是一条光滑的曲线,从图像上可以看 出:当Δx取不同的值时,可以得到不 同的割线;当Δx趋于零时,点B将沿 着曲线y=f(x)趋于点A,割线AB将绕 点A转动最后趋于直线l.直线l和曲线y =f(x)在点A处“相切”,称直线l为曲线y=f(x)在点A处的切 线.该切线的斜率就是函数y=f(x)在x0处的导数f′(x0).
第二章 §2
成才之路 ·高中新课程 ·学习指导 · 北师大版 ·数学 ·选修2-2
函数y=f(x)在x0处的导数,是曲线y=f(x)在点(x0,f(x0))处 的切线的斜率.函数y=f(x)在x0处切线的斜率反映了导数的几 何意义. 3.对导数的定义要注意两点:第一:Δx是自变量x在x0处 的改变量,所以Δx可正可负,但Δx≠0;第二:函数在某点的 导数,就是在该点的函数值改变量与自变量改变量之比的极限 值.因此它是一个常数而不是变数.
北师大版高中数学选修2-2:2
2
2
x
(2
x)
2 2
(2)
x x. 2 x
再计算相应的平均变化率
y
x 2 x
x
1
1.
x
x
2 x
当x趋于0时, 得到导数
f (2) lim y lim 1 1 1 1 1 .
x0 x x0 2 x 2
2
(3)首先, 对x x0给定自变量x的一个改变量x,得到相应函数值 的改变量
D.不能确定
【解析】
设切点(x0,y0),则f′(x0)=3x
2 0
=3,∴x0=
±1.
所以切线有2条.
【答案】 B
3.已知函数f(x)=3x,则f′(0)=________. 【解析】 f′(x)=(3x)′=3xln 3,则f′(0)=ln 3. 【答案】 ln 3 4.求曲线f(x)=cos x在点(0,f(0))处的切线方程.
则f (x)是关于x的函数, 称f (x)为f (x)的导函数, 通常
也简称为导数.
例题讲解
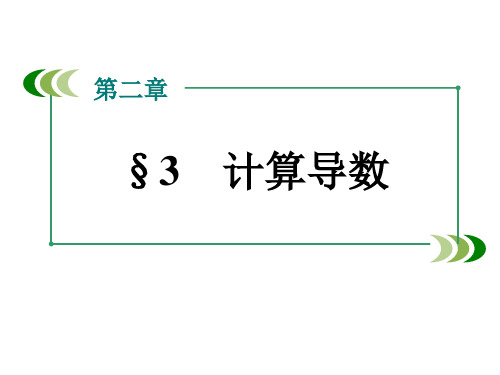
例3. 求y f (x) 3x2 x的导函数f (x),并利用导数f (x) 求f (1), f (2), f (0).
解 : 首先,给自变量x一个改变量x,得到相应函数值 的改变量: y f (x x) f (x) 3(x x)2 (x x) (3x2 x) 3x2 6xx x.
【解】∵f(0)=cos 0=1, 又 f′(x)=-sin x, ∴f′(0)=-sin 0=0,
∴曲线 f(x)=cos x 在点(0,f(0))处的切线方程为 y-1=0.
课常练习
已知函数 f(x)=x2-x,求 f′(x),并求 f′(2),f′(-2).
北师大版高中数学选修2-2第二章章末总结.docx

高中数学学习材料马鸣风萧萧*整理制作章末总结知识点一导数的概念平均变化率表示函数在某个区间内变化的快慢,瞬时变化率(导数)表示函数在某一点处变化的快慢.f′(x0)=limΔx→0f(x0+Δx)-f(x0)Δx.例1求函数y=f(x)=2x2+4x在x=3处的导数.例2航天飞机发射后的一段时间内,第t时的高度h(t)=5t3+30t2+45t+4,其中h的单位为m,t的单位为s.(1)h(0),h(1)分别表示什么;(2)求第1 s内高度的平均变化率;(3)求第1 s末高度的瞬时变化率,并说明它的意义.知识点二 导数的几何意义函数y =f (x )在x 0处的导数,是曲线y =f (x )在点(x 0,f (x 0))处切线的斜率,利用导数可以求曲线的切线斜率和切线方程.例3 已知曲线方程为y =x 2,(1)求过点A (2,4)且与曲线相切的直线方程;(2)求过点B (3,5)且与曲线相切的直线方程.例4 已知函数f (x )=ax 3+bx 2的图像经过点M (1,4),曲线在点M 处的切线恰好与直线x +9y =0垂直.(1)求实数a ,b 的值;(2)求过已知函数图像上某点处切线的斜率的取值范围.知识点三 导数的计算导数的计算主要考查导数公式的应用和导数的四则运算,复合函数的求导.在求导数时,一定要认清函数的形式,然后选择适当的公式和法则进行计算.例5 (1)求函数f (x )=4x 3在x =16处的导数;(2)求函数y =x 5+x +sin x x 2的导数; (3)求函数y =e sin(2x +3)的导数.知识点四 导数的实际意义实际生活中存在大量的变化率问题,我们可以根据导数计算并表示变化的快慢,在实际问题中理解导数的意义.例6 在受到制动后的t 秒内飞轮转过的角度(弧度)由函数φ(t )=4t -0.3t 2给出. 求:(1)t =2秒时,飞轮转过的角度;(2)飞轮停止旋转的时刻.例7 将原油精炼为汽油、柴油、塑胶等各种不同产品,需要对原油进行冷却和加热,如第x h 时,原油的温度(单位:℃)为f (x )=x 2-7x +15 (0≤x ≤18).求函数y =f (x )在x =6处的导数f ′(6),并解释它的实际意义.答 案重点解读例1 解 f ′(x )=lim Δx →02(x +Δx )2+4(x +Δx )-(2x 2+4x )Δx =lim Δx →04x ·Δx +2(Δx )2+4Δx Δx =lim Δx →0(4x +2Δx +4)=4x +4, ∴y ′|x =3=f ′(3)=4×3+4=16.例2 解 (1)h (0)表示航天飞机未发射时的高度,h (1)表示航天飞机发射1 s 后的高度. (2)Δh Δt =h (1)-h (0)1-0=80(m/s), 即第1 s 内高度的平均变化率为80 m/s.(3)h ′(1)=lim Δt →0 Δh Δt =lim Δt →0h (1+Δt )-h (1)Δt =lim Δt →0[5(Δt )2+45Δt +120]=120, 即第1 s 末高度的瞬时变化率为120 m/s.它说明在第1 s 末附近,航天飞机的高度大约以120 m/s 的速度增加.例3 解 (1)∵A (2,4)在y =x 2上.由y =x 2得,y ′=lim Δx →0f (x +Δx )-f (x )Δx =2x . ∴f ′(2)=4.∴切线方程为y -4=4(x -2),即4x -y -4=0.(2)设切点坐标为(x 0,x 20).由(1)得y ′=2x ,∴f ′(x 0)=2x 0.∴切线方程为y -x 20=2x 0(x -x 0).∵点(3,5)在切线上,∴5-x 20=2x 0(3-x 0).即x 20-6x 0+5=0.解得x 0=1或x 0=5,∴切线方程为2x -y -1=0或10x -y -25=0.例4 解 (1)因为y ′=f ′(x )=lim Δx →0a (x +Δx )3+b (x +Δx )2-ax 3-bx 2Δx =3ax 2+2bx .∵f (x )=ax 3+bx 2的图像过点M (1,4),∴a +b =4.又∵曲线在点M 处的切线与直线x +9y =0垂直,∴f ′(1)=9,∴3a +2b =9.由⎩⎪⎨⎪⎧ a +b =43a +2b =9得,⎩⎪⎨⎪⎧a =1b =3. (2)由(1)知y ′=f ′(x )=3ax 2+2bx =3x 2+6x=3(x +1)2-3≥-3.∴过已知函数图像上某点处的切线的斜率的取值范围是k ≥-3. 例5 解 (1)∵f ′(x )=(4x 3)′=(x 34)′=34x -14=344x, ∴f ′(16)=34·416=34×2=38. (2)∵y =x 3+x -32+sin x x 2, ∴y ′=(x 3)′+(x -32)′+(sin x )′x 2-(x 2)′sin x x 4=3x 2-32x -52+x 2cos x -2x sin x x 4=3x 2-32x -52+x -2cos x -2x -3sin x . (3)设y =e u ,u =sin t ,t =2x +3,则y ′=y ′u ·u ′t ·t ′x =e u cos t ×2=2e sin(2x +3)·cos(2x +3).例6 解 (1)t =2秒时,飞轮转过的角度φ(2)=8-1.2=6.8(弧度).(2)由题意得,φ′(t )=4-0.6t ,飞轮停止旋转,即瞬时角速度为0,所以令4-0.6t =0⇒t =203. 所以在t =203秒时飞轮停止转动. 例7 解 ∵f ′(x )=2x -7,∴f ′(6)=5.导数f ′(6)=5表示当x =6 h 时原油温度的瞬时变化率,即原油温度的瞬时变化速度.也就是说,如果保持6 h 时温度的变化速度,每经过1 h ,原油温度将升高5 ℃.。
高中数学北师大版选修2-2课件:第二章 复合函数的导数

4
9
例4、一个港口的某一观测点的水位在退潮的过程 中,水面高度y(单位:cm)。关于时间t(单位: s)的函数为 y h(t ) 100 ,求函数在t=3时的导数,
2t 1
并解释它的实际意义。
x (t ) 2t 1 复合而成的,其中x是中间变量。
yt h(t ) f ( x) (t )
[Cu( x)] Cu '( x)
法则3
u ' v uv ' u 2 v v
'
(v 0)
3
复合函数的导数
新授课
u 函数 y u , 3 x 2 , y ( 3 x 2) 构成间的关系? y ( 3 x 2)2 可由 y u 2 u 3 x 2复合得到. 与
2
复习:两个函数的和、差、积、商的 求导公式。 1、 常见函数的导数公式:
n n 1 C ' 0 (sin x)' cos x ( x )' nx (cos x)' sin x ' ' ' 2、法则1 [u ( x) v( x)] u ( x) v ( x) 法则2 [u( x)v( x)] u '( x)v( x) u( x)v '( x) ,
7
复合函数的导数
新授课 一般地,设函数 u ( x ) 在点 x 处有导数 u ( x ) ,函 x 数 y f (u) 在点 x 的对应点 u 处有导数 y f (u) ,则复合 u 函数 y f ( ( x )) 在点 x 处也有导数,且
y y u x u x
北师大版高中数学选修2-2第 二章《变化率与导数》
高中数学(北师大版)选修2-2教案:第2章 典型例题:导数与切线方程

导数与切线方程函数()y f x =在点0x 处的导数的几何意义,就是曲线()y f x =在点()()00,P x f x 处的切线的斜率,因此求曲线在某点处的切线方程,可以先求出函数在该点的导数,即曲线在该点的切线的斜率,再用直线的点斜式,写出直线的方程。
例、已知函数()316f x x x =+-.⑴求曲线()y f x =在点()2,6-处的切线的方程;⑵直线L 为曲线()y f x =的切线,且经过原点,求直线L 的方程及切点坐标;⑶如果曲线()y f x =的某一切线与直线134y x =-+垂直,求切点坐标与切线方程。
解析:⑴∵()()321631f x x x x ''=+-=+∴在点()2,6-处的切线的斜率为()2232113k f '==⨯+=,∴切线的方程为:()()1326y x =-+-,即136y x =-。
⑵法一、设切点为()00,x y ,则直线L 的斜率为()20031f x x '=+∴直线L 的方程为()()2200003116y x x x x x =+-++-又∵直线L 过点()0,0,∴()()22000003116x x x x =+-++-整理得,308x =-,∴02x =-,∴()()30221626y =-+--=-,∴13k = ∴直线L 的方程为13y x =,切点坐标为()2,26--。
法2、设直线L 的方程为y kx =,切点为()00,x y ,则3000000160y x x k x x -+-==- 又∵()30031k f x x '==+,∴3300001631x x x x +-=+,解得02x =-, ∴()()30221626y =-+--=-,13k =∴直线L 的方程为13y x =,切点坐标为()2,26--。
⑶∵切线与直线134y x =-+垂直,∴斜率4k = ∴设切点为()00,x y ,则()200314f x x '=+=,∴01x =±∴00114x y =⎧⎨=-⎩或00118x y =-⎧⎨=-⎩,∴切线方程为()4114y x =--或()4118y x =+- ∴即414y x =-或418y x =-点评:根据条件列方程或方程组是解决该问题的主要方法,灵活运用0x x =处的导数就是该点处的切线的斜率是解决有关问题的关键,由导数的几何意义可知,点()()00,x f x 处的切线方程()()()000y f x x x f x '=-+。
北师大版高中数学选修2-2 数学归纳法 课件(52张)
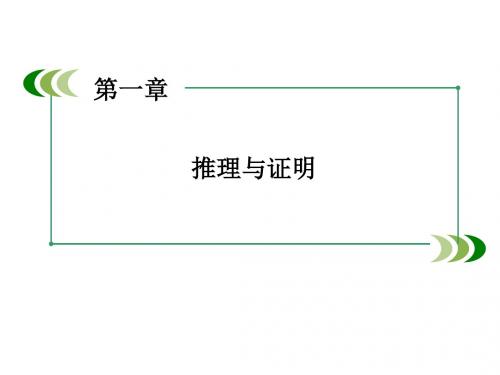
1 3 1 1 5 1 1 1 3.观察下列式子:1+22<2,1+22+32<3,1+22+32+42 7 <4,„,则可归纳出________.
[ 答案]
[ 解析]
2n+1 1 1 1 * 1+22+32+„+ < ( n ∈ N ) 2 n+1 n+1
(2)用数学归纳法证明有关问题的关键在于第二步,即n=k +1时为什么成立?n=k+1时成立是利用假设n=k时成立,根 据有关的定理、定义、公式、性质等数学结论推证出 n = k + 1 时成立,而不是直接代入,否则 n= k + 1 时也成假设了,命题
并没有得到证明。
(3)用数学归纳法可证明有关的正整数问题,但并不是所有 的正整数问题都是用数学归纳法证明的,学习时要具体问题具 体分析.
2.数学归纳法的核心 在验证命题 n = n0 正确的基础上,证明命题具有传递性, 第二步实际上是以一次逻辑的推理代替了无限的验证过程.所
以说数学归纳法是一种合理、切实可行的科学证题方法.实现
了有限到无限的飞跃.
1 1 1 1.用数学归纳法证明1+ 2 + 3 +„+ n <n(n∈N*,n>1) 2 -1 时,第一步应验证不等式________成立.
1.数学归纳法的原理和步骤的几个注意点: (1)奠基步骤和递推步骤这两个步骤缺一不可,只完成第一 步而缺少第二步就作出判断可能得出不正确的结论.因为单靠
第一步,无法递推下去,即n取n0以后的数时的命题是否正确,
我们无法判定,同样,只有第二步而缺少第一步时,也可能得 出不正确的结论,缺乏第一步这个基础,假设就失去了成立的 前提,第二步也就没有意义了.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
章末总结
知识点一导数的概念
平均变化率表示函数在某个区间内变化的快慢,瞬时变化率(导数)表示函数在某一点处变化的快慢.
f′(x0)=lim
Δx→0f(x0+Δx)-f(x0)
Δx
.
例
1求函数y=f(x)=2x2+4x在x=3处的导数.
例
2航天飞机发射后的一段时间内,第t时的高度h(t)=5t3+30t2+45t+4,其中h的单位为m,t的单位为s.
(1)h(0),h(1)分别表示什么;
(2)求第1s内高度的平均变化率;
(3)求第1s末高度的瞬时变化率,并说明它的意义.
知识点二导数的几何意义
函数y=f(x)在x0处的导数,是曲线y=f(x)在点(x0,f(x0))处切线的斜率,利用导数可以求曲线的切线斜率和切线方程.
例3已知曲线方程为y=x2,
(1)求过点A(2,4)且与曲线相切的直线方程;
(2)求过点B(3,5)且与曲线相切的直线方程.
例
4已知函数f(x)=ax3+bx2的图像经过点M(1,4),曲线在点M处的切线恰好与直线x+9y=0垂直.
(1)求实数a,b的值;
(2)求过已知函数图像上某点处切线的斜率的取值范围.
知识点三导数的计算
导数的计算主要考查导数公式的应用和导数的四则运算,复合函数的求导.在求导数时,一定要认清函数的形式,然后选择适当的公式和法则进行计算.
例
5
(1)求函数f (x )=4x 3
在x =16处的导数;
(2)求函数y =x 5+x +sin x
x 2
的导数;
(3)求函数y =e sin(2x +3)
的导数.
知识点四 导数的实际意义
实际生活中存在大量的变化率问题,我们可以根据导数计算并表示变化的快慢,在实际问题中理解导数的意义.
例
6在受到制动后的t秒内飞轮转过的角度(弧度)由函数φ(t)=4t-0.3t2给出.
求:(1)t=2秒时,飞轮转过的角度;
(2)飞轮停止旋转的时刻.
例
7将原油精炼为汽油、柴油、塑胶等各种不同产品,需要对原油进行冷却和加热,如第x h时,原油的温度(单位:℃)为f(x)=x2-7x +15(0≤x≤18).求函数y=f(x)在x=6处的导数f′(6),并解释它的实际意义.
答案
重点解读
例
1解f′(x)
=lim
Δx→02(x+Δx)2+4(x+Δx)-(2x2+4x)
Δx
=lim
Δx→04x·Δx+2(Δx)2+4Δx
Δx
=lim
Δx→0
(4x+2Δx+4)=4x+4,
∴y′|x=3=f′(3)=4×3+4=16.
例
2 解 (1)h (0)表示航天飞机未发射时的高度,h (1)表示航天飞机发射1s 后的高度.
(2)Δh Δt =h (1)-h (0)1-0
=80(m/s), 即第1s 内高度的平均变化率为80m/s.
(3)h ′(1)=lim Δt →0Δh Δt =lim Δt →0h (1+Δt )-h (1)Δt
=lim Δt →0
[5(Δt )2+45Δt +120]=120, 即第1s 末高度的瞬时变化率为120m/s.
它说明在第1s 末附近,航天飞机的高度大约以120m/s 的速度增加.
例
3解(1)∵A(2,4)在y=x2上.
由y=x2得,y′=lim
Δx→0f(x+Δx)-f(x)
Δx
=2x.
∴f′(2)=4.
∴切线方程为y-4=4(x-2),即4x-y-4=0.
(2)设切点坐标为(x0,x20).
由(1)得y′=2x,∴f′(x0)=2x0.
∴切线方程为y-x20=2x0(x-x0).
∵点(3,5)在切线上,∴5-x20=2x0(3-x0).
即x20-6x0+5=0.
解得x0=1或x0=5,
∴切线方程为2x-y-1=0或10x-y-25=0.
例
4 解 (1)因为y ′=f ′(x )
=lim Δx →0a (x +Δx )3+b (x +Δx )2-ax 3-bx 2
Δx
=3ax 2+2bx .
∵f (x )=ax 3+bx 2的图像过点M (1,4),
∴a +b =4.
又∵曲线在点M 处的切线与直线x +9y =0垂直,
∴f ′(1)=9,∴3a +2b =9.
由⎩⎪⎨⎪⎧ a +b =43a +2b =9得,⎩⎪⎨
⎪⎧ a =1
b =3.
(2)由(1)知y ′=f ′(x )=3ax 2+2bx =3x 2+6x
=3(x +1)2-3≥-3.
∴过已知函数图像上某点处的切线的斜率的取值范围是k ≥-3.
例
5 解 (1)∵f ′(x )=(4x 3)′=(x 34)′=34
x -14=
344x ,
∴f ′(16)=34·416
=
34×2=38. (2)∵y =x 3+x -32+sin x x 2, ∴y ′=(x 3)′+(x -32)′+(sin x )′x 2-(x 2)′sin x x 4
=3x 2-32x -52+x 2cos x -2x sin x x 4
=3x 2-32x -52
+x -2cos x -2x -3sin x . (3)设y =e u ,u =sin t ,t =2x +3,
则y ′=y ′u ·u ′t ·t ′x =e u cos t ×2
=2e sin(2x +3)·cos(2x +3). 例
6
解
(1)t =2秒时,飞轮转过的角度 φ(2)=8-1.2=6.8(弧度).
(2)由题意得,φ′(t )=4-0.6t ,
飞轮停止旋转,即瞬时角速度为0,
所以令4-0.6t =0⇒t =203.
所以在t =203秒时飞轮停止转动. 例
7解∵f′(x)=2x-7,∴f′(6)=5.
导数f′(6)=5表示当x=6h时原油温度的瞬时变化率,即原油温度的瞬时变化速度.也就是说,如果保持6h时温度的变化速度,每经过1h,原油温度将升高5℃.。
