§5.2 角动量的时间变化率 力矩(续)
合集下载
力矩的时间累积效应
又 L mR2
dt 1 d
故 LdL m2 gR3 cos θdθ
由题设条件积分上式
L LdL m2 gR3
cosd
0
0
L mR 3 2 (2g sin )1 2
L mR2 ( 2g sin )1 2
R
法二 现需求 L L( )
L mRv mR2
故需求 ( )
由质点定轴转动的转动定理
N
C
B
l
M
h A
l/2
设跷板是匀质的，长度为l，质量为m'，
跷板可绕中部支撑点C 在竖直平面内转动， 演员的质量均为m．假定演员M落在跷板上， 与跷板的碰撞是完全非弹性碰撞．
解 碰撞前M落在 A点的速度
vM (2gh)1 2
碰撞后的瞬间，M、N具有相同的线速度
u l
2
M、N和跷板组成的系统，角动量守恒
Mdt dL
t2 Mdt t1
L2 L1
dL
L2
L1
冲量矩
角动量定理的微分形式
1.质点 由：dL
r
F
M
dt
得：dL M dt
2.质点系
由：dL
dt
＝M外
得：dL M外dt
3.定轴刚体
由：M 轴
J
J
d
dt
得：Jd M轴d t
(二)、角动量定理的积分形式
瞬时
微分
效应
形式
Lz Liz ri2 mi
i
i
ri2 mi i
刚体对 z 轴的总角动量为：
Lz J
z
or
v
dm
2. 角动量定理
由刚体定轴转动定律
§2-5角动量定理 角动量守恒定律
太原理工大学物理系
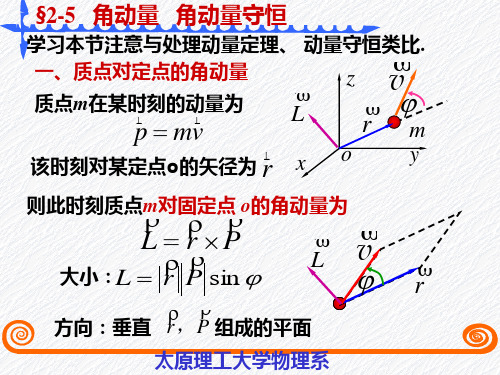
L r P
在直角坐标系中
L ( xi yj zk ) ( Px i Py j Pz k )
L x y z
i j k p x p y p z
太原理工大学物理系
L
v
方向：垂直 r ，P 组成的平面
太原理工大学物理系
r
讨论: 1) 同一质点相对于不同的点，角动量不同。 2) 在说明质点的角动量时，必须指明是对哪个 点而言的。
3）质点以角速度作半径为r的圆运动，相对 圆心的角动量
L = mvr
L
p
mr J
2
o r
2）在具体的坐标系中，角动量在各坐标轴的分 量称作对轴的角动量。力矩在各坐标轴的分量， 称作对轴的力矩。
L Lx i Ly j Lz k L 是质点对o点的角动量
Lx Ly Lz
分别是质点对x、y、z轴的角动量.
M M x i M y j M z k M 是力对o点的力矩
三、质点的角动量定理 dP 由牛顿第二定律 F dt
dP 两边用位矢叉乘 r F r dt dp d dr r (r p) p dt dt dt
dr 由速度定义 v dt
v p 0 dL dp d r (r p) dt dt dt
i
ri fi 质点系受到的内力矩的矢量和
i
矩
太原理工大学物理系
可以证明：内力对定点的力矩之和为零，即
ri fi 0
i
质点系内的重要结论之三
角动量变化定理
理学院物理系陈强第5章角动量变化定理与角动量守恒§5-1. 角动量与力矩§5-2. 质点的角动量变化定理角动量守恒§5-3.质点组的角动量变化定理角动量守恒§5-4.有心运动12理学院物理系陈强第5章角动量变化定理与角动量守恒一.质点的角动量(动量矩)v m r p r L r r r r r ×≡×≡又称动量矩Oαdpr L1.定义：在惯性参考系中选一固定的参考点O ，运动质点对O 点的位矢r ,动量为p ,则质点对O 点的角动量为:mvdsin rmv sin rp L ===ααα为r 和p 两矢量间的夹角角动量L 的大小：§5-1. 角动量与力矩垂直于矢径r 和动量p 所组成的平面，角动量L 的方向：指向由右手螺旋法则确定.3理学院物理系陈强第5章角动量变化定理与角动量守恒mαO L = rmvL r v例：•角动量的大小和方向不仅决定于质点的运动也依赖于所选定的参考点，参考点不同，质点的动量矩不同。
注意:•角动量的单位千克·米2/秒（kg ·m 2/s)水平面上质点做匀速圆周运动4理学院物理系陈强第5章角动量变化定理与角动量守恒例如：vr r r m r L om O ×=vlm L O =方向变化v r r r m r L m o O ×=′′αsin v lm L O =′方向竖直向上不变O l αv r O ′锥摆m5理学院物理系陈强第5章角动量变化定理与角动量守恒2.角动量的分量表示v m r p r L rr r r r ×≡×≡在直角坐标系中：yz y z x m z ym zp yp L v v −=−=zx x y m zm zp L v v x xp z −=−=xy x y z m y xm yp xp L v v −=−=()z y x z y x p p p zy x k j i L ,L ,L r rr =kL j L i L L z y x rrrr ++==L r6理学院物理系陈强第5章角动量变化定理与角动量守恒二.力矩即F r M r r r ×=力矩的大小：Fr sin rF M 0==ααsin r r 0=——称力臂。
角动量 角动量守恒定律
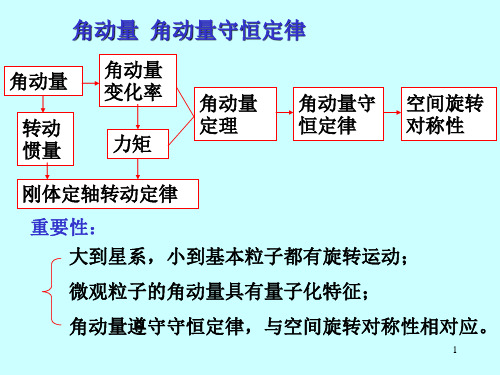
r为力的作用点到 参考点的位置矢量
20
2) 力对定轴的力矩
z
Mz
o
d
F F //
r
F
M r F r ( F// F ) r F// r F
第一项
力F对O点的力矩 （F不在转动平面内）：
M1 r F//
dL 可得 M r F dt
对 N 个质点 m1, m2 ,, mN 组成的质点系，由
dL1 r1 F1外 F1内 M 1外 M 1内 dt 两边求和得 dL2 r2 F2外 F2内 M 2外 M 2内 dL总 d dt Li dt i dt M i 外 M i内 dLN i i 24 rN FN外 FN内 M N外 M N内 dt
z
vi
转轴与其转动平面交点
o
转动 平面
mi 对 o 的角动量： Lio ri mi vi
大小：Lio ri mi vi mi ri 2 Lio 方向：沿 2 即 Lio mi ri
o圆周运动半径为 ri
o ri
mi
6
定义：质点 mi 对其转动平面上圆心 o 点的角动 量的大小，称为质点对转轴的角动量。
11
m 1 L3 L3 1 2 m L 12 L 3 8 8
(2) 轴过一端端点
dm
o
x
J r dm x dm
2 2 L
L
x
2
若使用平行轴定理：
0
角动量.pdf
r rc′ =
i
r ∑ mi ri′
i
与 i 无关
M
r × vC
由
r ∑ mi ri M
r ∑ mi ri′ M
∑
i
r r r r ri ′ × m i v c = M rc′ × v c = 0
质心对自己的位矢
r r r r r r r L = rc × ∑ mi vi + ∑ ri′× mi vc + ∑ ri′× mi vi′
r p1
i i i
r r r ri = rc + ri′ Q r r r v i = v c + v i′
有'：对质心 无'：对参考点
rr r r1rc r 2
r cp2
r ri′ θ θ
rr p pii
∴
与i无关
r r r r L = ∑ (rc + ri′) × m i v i
i i i
*质点对某参考点的角动量反映质点绕该参考点旋 转运动的强弱。 转运动的强弱。 *必须指明参考点， 必须指明参考点，角动量才有实际意义。 角动量才有实际意义。
2. 质点系角动量
r r r r r r L = ∑ Li = ∑ ri × pi = ∑ ri × mi vi
系统内所有质点对同一参考点 系统内所有质点对同一参考点角动量的矢量和 同一参考点角动量的矢量和
J = ∫ r 2dm 积分元选取： 积分元选取：
λdl
J = ∫ r dm
2
线密度： 线密度： λ , 线元： 线元： d l
面密度： 面密度： σ , 面元： 面元： dS
体密度： 体密度： ρ , 体元： 体元： dV
i
r ∑ mi ri′
i
与 i 无关
M
r × vC
由
r ∑ mi ri M
r ∑ mi ri′ M
∑
i
r r r r ri ′ × m i v c = M rc′ × v c = 0
质心对自己的位矢
r r r r r r r L = rc × ∑ mi vi + ∑ ri′× mi vc + ∑ ri′× mi vi′
r p1
i i i
r r r ri = rc + ri′ Q r r r v i = v c + v i′
有'：对质心 无'：对参考点
rr r r1rc r 2
r cp2
r ri′ θ θ
rr p pii
∴
与i无关
r r r r L = ∑ (rc + ri′) × m i v i
i i i
*质点对某参考点的角动量反映质点绕该参考点旋 转运动的强弱。 转运动的强弱。 *必须指明参考点， 必须指明参考点，角动量才有实际意义。 角动量才有实际意义。
2. 质点系角动量
r r r r r r L = ∑ Li = ∑ ri × pi = ∑ ri × mi vi
系统内所有质点对同一参考点 系统内所有质点对同一参考点角动量的矢量和 同一参考点角动量的矢量和
J = ∫ r 2dm 积分元选取： 积分元选取：
λdl
J = ∫ r dm
2
线密度： 线密度： λ , 线元： 线元： d l
面密度： 面密度： σ , 面元： 面元： dS
体密度： 体密度： ρ , 体元： 体元： dV
5.2 质点的角动量定理与角动量定理定律
21
5.2 质点的角动量定理与角动量守恒定律 第5章 刚体的定轴转动
例：质量为Ｍ的圆锥摆摆球，以速率 v 运动时， 判断：1）对Ｏ参考点的角动量是否守恒？
2）对Ｃ参考点的角动量是否守恒？
2）以C为参考点。
重力矩：
r M
=
r l
×
mgr
M = lmg sin θ
张力矩：
r M
=
r l
×
r T
=
0
lθ c
16世纪末至17世纪初，开普勒仔细地分析整理了 前人记录下的大量精确的有关行星运动的资料，总 结出行星运动的规律、即开普勒三定律。
rrr
r M
=
rr ×
r F
=
i x
j y
k
r
r
r
z = Mxi + My j + Mzk
Fx Fy Fz
8
5.2 质点的角动量定理与角动量守恒定律 第5章 刚体的定轴转动
rrr
r M
=
rr
×
r F
=
i x
j y
k z
Fx Fy Fz
其中：
⎧ ⎪
M
x
=
yFz
−
zFy
⎨M y = zFx − xFz
r
注意：定理中的力矩和角动量都必须是相对于同 一参考点而言的。
说明: 1）冲量矩是质点角动量变化的原因。
2）质点角动量的变化是力矩对时间的积累结果。 17
5.2 质点的角动量定理与角动量守恒定律 第5章 刚体的定轴转动
四、质点的角动量守恒定律
当
v M
=
0
,
时，
5-2 质点系的角动量定理及角动量守恒定律
若质点系的所有质点均分别在与 z 轴垂直的平 面内运动，且一共同的角速度绕 z 轴作圆周运动， 则质点系对 z 轴的角动量为
Lz ri mi vi mi ri
i i
2
当质点系对轴的角动量守恒时：
ri 变小，则
M z 0 ，Lz 常量
增大；
ri 变大，则
减小.
质点系对轴的角动量定理
质点系对轴的角动量定理
dLz Mz dt
如果在一个过程中，质点系所受的外力 对 z 轴的力矩始终保持为零，则质点系对该 轴的角动量守恒.
M z 0 ，Lz 常量
质点系对轴的角动量守恒定律
当内力矩远大于外力矩时，质点系对轴的角动量 也是守恒的. （例：P170例1）
在直角坐标系中，上式沿三个坐标轴的投影式为
dLy dLx dLz M x M ix , My , Mz . dt dt dt
• 如果只考虑上式中某一个分量，例如 z 分量，则 表现为对轴的特征：即质点系对于 z 轴的角动量对时 间的变化率等于质点系所受一切外力对 z 轴力矩的代 数和，叫做质点系对 z 轴的角动量定理。
ri fij rj f ji (ri rj ) fij 0
ri fij 0
i i j
成对出现的内力对参考点的力矩矢量和为零. 由于系统内力总是成对出现，则系统内力矩的矢量和为零. • 可见，系统的内力矩只能使系统内各质点的角动量改变， 但不能改变质点系总的角动量。
如果在一个过程中，始终无外力矩作用或所受 的外力矩为零，则质点系的总角动量守恒 .
M外 0 ，L 常矢量
质点系对某一固定点的角动量守恒定律
大学物理角动量 角动量守恒定律
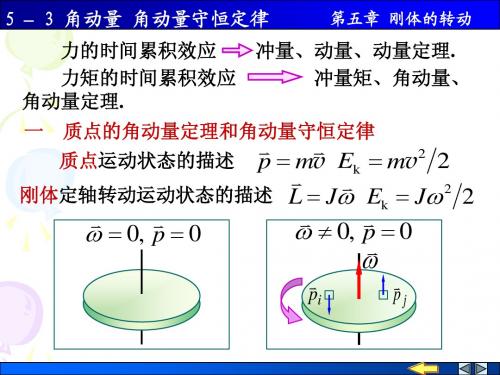
解 小虫与细杆的碰撞视为完全非弹性碰撞，碰撞 前后系统角动量守恒
1 mv0 ml 12 4 l
2
m( ) 4 l
2
12 v 0 7 l
5 – 3 角动量 角动量守恒定律
12 v 0 7 l
第五章 刚体的转动
由角动量定理
M dL dt d ( J ) dt dJ dt
第五章 刚体的转动
v A (v0 v ) 1 v B 1709 m s
mM m R h
2
2
1 2
飞船在 A点喷出气体后, 在到 达月球的过程中, 机械能守恒
1 2 m v A G 1 2
2
vB
B
vA
v0
R
O h
v
u
2
A
m v B G
2
2
mM m
质点的角动量定理和角动量守恒定律
pi
pj
5 – 3 角动量 角动量守恒定律
第五章 刚体的转动
1 质点的角动量 质量为 m 的质点以速度 v 在空间运动，某时刻相对原点 O 的位矢为 r ，质点相对于原 点的角动量
L
z
v
r
o
L r p r mv 大小 L rm v sin
第五章 刚体的转动
二
刚体定轴转动的角动量定理和角动量守恒定律
1 刚体定轴转动的角动量
L
i
m i ri v i ( m i ri )
2 i
z
O ri
mi
L J
2 刚体定轴转动的角动量定理
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解得：
a
(
m
mgs
1 2
M
)l
§5.3 角动量定理
一、角动量定理的微分形式
1.质点 由 ：dL
r
F
M
dt
得：dL M dt
2.质点由系：dL＝M dt
外
得：dL M外dt
3.定轴刚体
由 ：M 轴
J
J
d
dt
得：Jd M轴d t
二、角动量定理的积分形式
瞬时
微分
效应
形式
质点
M
dL
dL Mdt
dt
质点系
M外
dL dt
dL M外dt
积分形式 （有限时间过程）
t2
M
dt
L2dL
L
t1
L1
t2
t1
M外dt
L2dL
L
L1
定轴 刚体
M轴 J
Jd M轴d t
t2 M轴dt t1
2 Jd
1
J
注意
1. 力矩对时间的积累：角冲量（冲量矩）
t 2
定义： 2.比较：
用电子在外磁场中的旋进解释物质 f
的磁化的本质；
…...
Байду номын сангаас
v
rc
mg
录像片：1－2－9 角动量守恒定律 10分钟
m2 g
m1 : 向下为正 m1g T1 m1a1 ( 1 ) m2 : 向上为正 T2 m2 g m2a2 ( 2 )
思考：
a1 a2 ? T1 ×T2 ?
N
+
r
滑轮 m：以顺时针方向为正方向
T1r
T2r
J
1 mr2
2
(3)
T2 m g
T1
四个未知数：a1 a2 a, T1 , T2 ,
同 学 们 好
上讲 §5.1 角动量 转动惯量
1.角动量
质点
L r p r mv
质点系 L rc Mv c ri mivi L轨道 L自旋
i
定轴刚体 Lz ri2mi J
i
*必须指明参考点，角动量才有实际意义。
2. 转动惯量
J ri2mi
i
J r 2dm
m
A
M
r o
B
CB
CA x2 B
s
A x1
x
T1
. CA
＋
mAg
T2 ＋
CB .
mBg
＋
A
J
o
r
B
T2 T1
mA g T1 mAa
T2 mB g mBa
T1r T2r Jβ
J
JM
J AB
1 2
Mr 2
m AB r 2
m
A
M
r o
B
CB
CA x2 B
s
A x1
x
又： a r
s x1 x2
旋进角速度： Ω d dL M
dt Lsin dt Lsin
( )
3.车轮的旋进
o
Ω
o
L
L
dL
M
讨论：•改变 的方向，旋进方向是否改变？
•改变配重 G ，对旋进有什么影响？ •用外力矩加速（或阻碍）旋进，会发生 什么现象？
1. 2. 3
4、炮弹的旋进
5、旋进现象在自然界广泛存在：
地球的旋进；
F21
m
2
r2
F23 F32
F31 m3
r3 F3外
dL dt
d dt
(L1
L2
LN )
质点角动量的时间 变化率
dLi dt
ri Fi
Mi
dL1 dt dL2 dt
M1外 M1内
M 2外 M 2内
dLN dt
M N外 M N内
两边求和得
d
dL
dt
i
Li
dt
M i外 M i内
i
i
?
由图可知
Mi内 0
i
o r2 r1 d
f12
1
m1
f 21
2
m2
于是
dL
dt M 外 i ri Fi外
质点系总角动量的时间变化率等于质点系所受 外力矩的矢量和 (合外力矩 )
注意1： 合外力矩 M外 是质点系所受各外力矩的
矢量和，而非合力的力矩。
注意2：质点系内力矩的作用
0
2
得
2m k L2 ,
2m rdr dm L2
dm
2m rdr L2
df dm g 2m g
L2 rdr
dM rdf
z
r
df
o
dm
M
dM
L 0
2m g
L2
r 2dr
2 3
m gL
实际意义
f
f
r
oR
等效
z
df o
dm
r
半径 R ，质量 m 的匀质圆盘，与桌
面间摩擦系数 µ，
积分元的选取 积分限的确定
§5.2 角动量的时间变化率 力矩(续)
一、由质点：角L动=量r的×时p 间变化率dL
r
F
dt
二、力矩
1. 对参考点的力矩： M r F
质点角动量的时间变化率等于质点所受的合力矩
2. 对z轴的力矩:对参考点的力矩在z轴上的投影。
M z xFy yFx Mz r F
求摩擦力矩
简化模型：
长 R ，线密度 kr
总质量 m 的细杆
四. 刚体定轴转动定律
dL
M外 dt
Mz
dLz dt
由 Lz J
得
Mz
=
dLz dt
=
d dt
(Jω) =
J
dω dt
=
Jβ
Mz J 刚体定轴转动定律
力矩的瞬时效应是产生角加速度
比较
F ma －矢量式
Mz
J
－标量式
F 改变物体平动状态的原因
三个方程 ？
绳与滑轮间无相对滑动，由角量和线量的关系：
a r
(4)
解得 m1 m2 g
m1
m2
1 2
m
r
0
t
m1 m2 gt
m1
m2
1 2
m
r
练习1.
半径如m为图示。，已两知物体r 与质桌量面分间别m的为2滑m和动1摩擦，m系滑2 数轮为质量，为求 ，
下落的加速度m和1两段绳中的张力。
m2
ro m
m1
解：在地面参考系中，选取m1、m和2 滑轮为研究对
象，分别运用牛顿定律和刚体定轴转动定律得：
T1
m1
a
m1 g
Na
m2 g m2
T2
m2 g
T2
Ny
o
Nx
向里+
T1
列方程如下： 可求解
m1 g T1 m1a
T2 m2 g m2a
( T1
T2
)r
1 2
m r2
a r
例2. 质量为 M 的匀质圆盘，可绕通过盘中心垂直于盘的固定 光滑轴转动，绕过盘的边缘有质量为 m、长为 l 的匀质柔软绳 索（如图）。设绳与圆盘无相对滑动，试求当圆盘两侧绳长差 为 s 时，绳的加速度的大小。
mg L ， 的大小，
只改变 L 的方向。
使陀螺绕竖直轴旋转——旋进
L
rc
o
mg
M rc mg L
d
dL
L L
o
M
dL
dt
dL L
d
L
o
Ω d
dt dL L
重力矩始终不改变角动量的大小，只改变角动量的方 向。形成角速度矢量不断向外力矩方向靠拢的趋势。
最终效果：陀螺绕竖直轴旋转——旋进
1.回转仪实验： 如图所示的杠杆陀螺
仪。当陀螺仪高速旋转
时，移动平衡物B，杆
不会倾斜，而是在水平
面内绕O旋转。这种运
动称为旋进运动，它是 在外力矩作用下产生的 回转效应。
2.陀螺 o
(1) 若L 0 在重力矩
时： rc
m
g
作用下，
陀螺将绕垂直于黑板的轴转动，
即倒地。
（2）当 L 0 时：
重将力不矩改变rcL
m 是物体平动惯性的量度。
M z 改变物体绕轴转动状态的原因
J 是物体转动惯性的量度。
F ma
Mz J
平动问题 刚体定轴转动问题
地位相同
例1: 一定滑轮的质量为 m，半径为 ，r一轻绳两边
分别系 和 m两1 物m体2挂于滑轮上，绳不伸长，绳与
滑轮间无相对滑动。不计轴的摩擦，初角速度为零， 求滑轮转动角速度随时间变化的规律。
m
A
M
r o
B
x2 B
A x1 s
x
解：在地面参考系中，建立如图 x 坐标，设绳两端坐标分别为x1，x2， 滑轮半径为 r 有：
l AA AB BB x1 x2 r
m mAA l x1 ,
m mBB l x2 ,
mAB
m l
r
s x1 x2
用隔离法列方程：（以逆时针方向为正）
m
r
已知：
m , m1 , m2 , r , 0 0
求： t ?
m2
思路：
m1 质点平动与刚体定轴转动关联问题
十六字诀
先求角加速度
解：在地面参考系中，分别以 m1 , m2 , m