习题课6-力矩与角动量
力矩、角动量定理和刚体.ppt

转动动能
1 2 Ek mi vi i 2 1 1 2 2 2 ( mi ri ) J 2 i 2
36
刚体绕定轴转动的动能定理 1 2 2 d d Jd W Md J 1 1 1 dt 2 1 1 2 2 W Md J 2 J1 1 2 2
例
相对不同参考点A、B,计算重力矩和角动量
参考点A: 重力矩 角动量 参考点B: 重力矩 角动量
A
v
mg
d1
M mgd 1
L0
d2
B
M mgd 1
L mvd2
(三)
质点对轴的角动量定理及守恒
dL z Mz dt
§4.2 质点系的角动量定理
1、质点系的角动量 2、质点系的角动量定理 3、角动量守恒 4、绕某一轴的圆周运动
该直线称作转轴。
对定轴转动的描述:角坐标。一个自由度。
刚体转动的角速度和角加速度 z 角坐标 (t )
沿逆时针方向转动 > 0 沿顺时针方向转动 < 0 角位移 (t t) (t) 角速度 角加速度
O
ω
d P(t)
r P’(.t+dt)
.
x
d lim t 0 t dt
I m r r dm
2 j j 2 j
dm:质量元 d V :体积元
r dV
2 V
说明 刚体的转动惯量与以下因素有关:
(1)与刚体的几何形状及质量分布有关. (2)与转轴的位置有关.
平行轴定理
质量为m 的刚体, 如果对其质心轴的转动 惯量为 I C ,则对任一与 该轴平行,相距为 d 的 转轴的转动惯量
力矩和角动量的积分计算题目及解析

力矩和角动量的积分计算题目及解析
摘要:
I.引言
A.力矩和角动量的概念
B.力矩和角动量积分的应用
II.力矩和角动量的积分计算方法
A.力矩的定义和计算公式
B.角动量的定义和计算公式
C.力矩和角动量积分的计算方法
III.力矩和角动量积分计算题目解析
A.计算题目的类型
B.解题的步骤和方法
C.需要注意的计算细节
IV.结论
A.力矩和角动量积分计算的重要性
B.计算中的常见问题和解决方法
C.展望未来的研究方向
正文:
力矩和角动量是物理学中非常重要的概念,它们在许多物理问题的研究中都有着广泛的应用。
在实际问题中,我们常常需要对力矩和角动量进行积分计算,以便更好地理解和分析物理现象。
因此,掌握力矩和角动量积分的计算方
法是非常必要的。
首先,我们需要了解力矩和角动量的定义和计算公式。
力矩是一个向量,它的方向垂直于力的作用线,大小等于力的大小与力臂的乘积。
角动量是一个矢量,它的方向沿着物体绕某个轴旋转的方向,大小等于物体的质量、速度和旋转半径的乘积。
在此基础上,我们可以推导出力矩和角动量的计算公式,并利用这些公式进行积分计算。
在实际计算中,我们需要注意一些细节问题。
例如,在进行积分计算时,我们需要根据题目的要求选择合适的积分方法。
此外,我们还需要注意公式的适用范围,避免在计算过程中出现错误。
总之,力矩和角动量积分计算在物理学中有着广泛的应用,掌握其计算方法对于解决物理问题具有重要意义。
在实际计算中,我们需要注意细节问题,选择合适的计算方法,并灵活运用公式。
力矩、转动定律、角动量守恒

mgl 1 mgl 1 mv2 v gl 4g
2
2
l
P24 1-6: As shown in below figure, the body A is connected to the body B by the light rope which is through uniform solid cylinder(圆柱体) with a mass Mand a radius R. The body A has a mass of m1 and the mass of B is m2.There is not relative motion between the rope and cylinder. Find the tension force between the solid cylinders with
a R
(4)以上三式联立,可得物体 下落的加速度和张力:
a
m2
m2
m1 2
g
T m1m2 g 2m2 m1
m2 R(m2
m1 ) 2
g
o m1
m2 x
P34.习题19 质量为m、长为L的均质细杆可绕水平光滑轴O在竖直 平面内转动。若使杆从水平位置开始由静止释放,试求杆转至铅垂
T=?
J 1 MR2 2
M,R
m1 A
B m2
解:⑴ 研究对象:A、B和圆柱体; ⑵ 受力分析如图:
A向上运动,有加速度aA,B向下运动,加速 度aB,圆柱体顺时针转动。
T
T
T
A
B
T
m1g m2g
T
T1
T2
T2
(3)列方程:
角动量(习题)
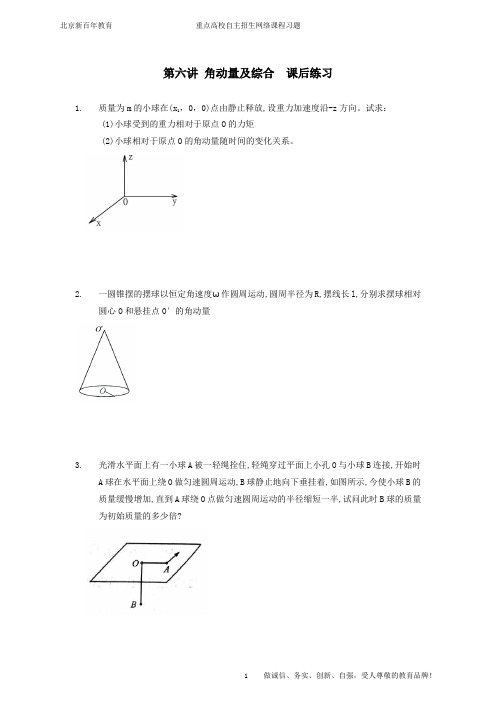
第六讲角动量及综合课后练习1.质量为m的小球在(x1,0,0)点由静止释放,设重力加速度沿-z方向。
试求:(1)小球受到的重力相对于原点O的力矩(2)小球相对于原点O的角动量随时间的变化关系。
2.一圆锥摆的摆球以恒定角速度ω作圆周运动,圆周半径为R,摆线长l,分别求摆球相对圆心O和悬挂点O′的角动量3.光滑水平面上有一小球A被一轻绳拴住,轻绳穿过平面上小孔O与小球B连接,开始时A球在水平面上绕O做匀速圆周运动,B球静止地向下垂挂着,如图所示,今使小球B的质量缓慢增加,直到A球绕O点做匀速圆周运动的半径缩短一半,试问此时B球的质量为初始质量的多少倍?4.在光滑水平面上,一个质量为m的质点系于一根原长为a的轻橡皮绳的一端,橡皮绳的另一端系于桌面上一个固定点O,橡皮绳拉伸时的劲度系数为k,若质点在开始时被拉至距O点距离为2a处,并给质点在垂直于橡皮绳方向以初速度V。
(1)为使质点绕O点作圆周运动,求V的大小(2)为使橡皮绳不松弛,V的最小值V m(3)当0<V<V m时,质点在运动中距O点的最小距离为多大5.一质量为m的物体栓在穿过小孔的轻绳的一端,在光滑的水平台面以角速度ω0作半径为r0的圆周运动,自t=0时刻开始,手拉着绳子的另一端以匀速v向下运动,使半径逐渐减小,试求:(1)角速度与时间关系ω(t);(2)绳中的张力与时间关系。
6.如图所示,质量为m的小球系在绳子的一端,绳穿过一铅直套管,使小球限制在一光滑水平面上运动。
先使小球以速度v0绕管心作半径为r0的圆周运动,然后向下慢慢拉绳,使小球运动轨迹最后成为半径为r1的圆,求(1)小球距管心r1时速度大小(2)由r0缩到r1过程中,力F所作的功7.在一根长为3l的轻杆上打一个小孔,孔离一端的距离为l,再在杆的两端以及距另一端为l处各系一质量为M的小球,然后通过此孔将杆悬挂于一光滑的水平细轴O上,如图所示,开始时,轻杆静止,一质量为m的小球以水平速度v0射入中间的小球,并留在里面,试求杆在以后摆动中的最大摆角。
牛顿力学:角动量和力矩

力矩的定义:力与力臂的乘积
力矩的分类:静态力矩和动态力矩
静态力矩:力与力臂的乘积,用于描述物体在静止状态下的转动情况
动态力矩:力与力臂的乘积,用于描述物体在运动状态下的转动情况
实例
开门:门把手的转动产生力矩,使门打开
自行车:脚踏板的转动产生力矩,使自行车前进
扳手:扳手的转动产生力矩,使螺栓拧紧或松开
角动量的计算公式:L=r×p,其中r是质点到旋转轴的距离,p是质点的动量
角动量的单位:国际单位制中的单位是kg·m²/s
角动量的方向:角动量的方向与力矩的方向相同,与旋转轴的方向垂直
实例
地球自转:角动量守恒原理在地球自转中的应用
冰上运动员:角动量守恒原理在冰上运动员旋转中的应用
自行车:角动量守恒原理在自行车行驶中的应用
陀螺仪:角动量守恒原理在陀螺仪中的应用
力矩
3
定义
Байду номын сангаас
力矩:力与力臂的乘积
力矩的方向:垂直于力臂,与力同向或反向
力臂:力作用点到转动轴的距离
计算方法
力矩的定义:力与力臂的乘积
力矩的计算公式:M=F*L
力矩的方向:与力臂垂直,与力同向
力矩的性质:力矩的大小与力的大小、力臂的长度以及两者之间的夹角有关
分类
拧开瓶盖:瓶盖的转动产生力矩,使瓶盖拧开
感谢观看
汇报人:XX
性质:角动量是守恒的,即一个封闭系统中的角动量总和保持不变
守恒定律
角动量守恒的应用:解释天体运动、陀螺仪等物理现象
角动量守恒定律:在封闭系统中,角动量总是守恒的
角动量守恒的条件:系统不受外力矩作用,或者外力矩的矢量和为零
角动量守恒与能量守恒的关系:角动量守恒是能量守恒的一种表现形式
大学物理力矩与角动量

z
z
M
Fz
F
Fx
ˆF ˆ ˆ F Fx i j F k y z ˆM ˆ ˆ M M xi j M k y z
o
r
P
Fy
x
y
y
x
ˆ yj ˆ zk ˆ ) (F i ˆF ˆ ˆ) ( xi j F k x y z ˆ xF ˆ ˆ ˆ ˆ ˆ xFy k z j yFx k yFz i zFx j zF y i ˆ ( zF xF ) ˆ ˆ ( yFz zFy )i x z j ( xF y yFx )k
5
一、力矩(moment of force)
6
力对参考点的力矩 定义:作用于质点 P 的力 F 对参考点 O 的力矩等于力的作用 点位矢与力的叉积,即:
M r F
大小
M | M | rF sin Fd F r
M
F
F
O
方向
r、F、M 成右手螺旋关系。
d
r
P
M内 ri f ij 0
i 1, i j n
f ij
mi
ri
ri j
mj
o
rj
f ji
即:质点组内力矩的矢量和恒为零,只需考虑外力矩。
23
对质点系的所有质点应用角动量定理并取和
M 外 ri Fi 外 dLi d dL ( Li ) dt dt dt
质点对参考点的角动量的增量等于作 用于质点的力对同一参考点的角冲量 (angular impulse)。
L2 L1 Mdt
16
专题六:力矩和角动量

专题六:力矩和角动量例1.如图所示,一个质量均匀分布的直杆搁置在质量均匀的圆环上,杆与圆环相切,系统静止在水平地面上,杆与地面接触点为A ,与环面接触点为B 。
已知两个物体的质量线密度均为ρ,直杆与地面的夹角为θ,圆环半径为R ,所有接触点的摩擦力足够大。
求:(1)地给圆环的摩擦力;(2)求A 、B 两点静摩擦因数的取值范围。
例2.有一轻质木板AB 长为L ,A 端用铰链固定在竖直墙上,另一端用水平轻绳CB 拉住。
板上依次放着A 、B 、C 三个圆柱体,半径均为r ,重均为G ,木板与墙的夹角为θ,如图所示,不计一切摩擦,求BC 绳上的张力。
例3.有一质量为m =50kg 的直杆,竖立在水平地面上,杆与地面间静摩擦因数μ=0.3,杆的上端由固定在地面上的绳索拉住,绳与杆的夹角θ=300,如图所示。
(1)若以水平力F 作用在杆上,作用点到地面的距离h 1=2L /5(L 为杆长),要使杆不滑倒,力F 最大不能超过多少?(2)若将作用点移到h 2=4L /5处时,情况又如何?例4.如图所示,矩形板N 上有两个光滑的圆柱,还有三个小孔A 、B 、C ,通 过小孔可以用销钉把此板固定在光滑的水平面M 上。
一柔性带按图示方式绕过 两圆柱后,两端被施以拉力T'=T =600 N ,且T'∥T ,相距40 cm ;已知AB = 30 cm ,AC =145 cm ,BC =150 cm 。
为了保持物块静止,(1)若将两个销钉分别插入A 、B 中,这两个孔将受受怎样的力?(2)将两个销钉插入哪两个孔才最省力?此时所插的销钉受力多大?例5. 如图所示,质量为 m 的小球 B 放在光滑的水平A B θ槽内,现以一长为l 的细绳连接另一质量为m 的小球A ,开始时细绳处于松弛状态, A 与B 相距为l /2。
球A 以初速度v 0在光滑的水平地面上向右运动。
当A 运动到图示某一位置时细绳被拉紧,试求B 球开始运动时速度v B 的大小。
力学 角动量 习题

解:设滑轮半径为R,弹簧释放后 弹簧上 设滑轮半径为 ,弹簧释放后, ⊙ 边砝码获得的速度为v,方向向上, 边砝码获得的速度为 ,方向向上,左边砝 码盘获得的速度为v',方向向下, 码盘获得的速度为 ,方向向下 右边砝码 v v' m 盘及砝码获得的速度也是v',但方向向上 盘及砝码获得的速度也是 但方向向上 m 把左盘, 把左盘 左盘上的砝码和右盘及盘中砝码视 m m v' 为一个质点系, 为一个质点系 在弹簧释放过程质点系对轮 轴的角动量守恒: 轴的角动量守恒:- mvR+mv'R+2mv'R = 0,即 v = 3 v' (1) , 另外,质点系能量守恒,忽略重力势能的微小变化,则有: 另外,质点系能量守恒,忽略重力势能的微小变化,则有: 2 1 kl0 = 1 mv 2 + 1 ( 3m )v'2 即,mv 2 + 3mv '2 = kl0 2 ( 2) 2 2 2 左盘中的砝码脱离弹簧获得速度v后做竖直上抛运动 达到最 左盘中的砝码脱离弹簧获得速度 后做竖直上抛运动,达到最 后做竖直上抛运动 大高度h时速度为零 据能量守恒, 2 时速度为零,据能量守恒 大高度 时速度为零 据能量守恒 1 mv 2 = mgh ∴ h = v 2 / 2 g ( 3) 由⑴⑵可求得 v2=3kl02/4m,代入⑶中得:h = 3 k l02/8mg ⑴⑵可求得 ,代入⑶中得:
5.2.3 两个滑冰运动员的质量各为 两个滑冰运动员的质量各为70kg,以6.5m/s的速率沿相反方向 , 的速率沿相反方向 滑行,滑行路线间的垂直距离为10m,当彼此交错时 各抓住 滑行,滑行路线间的垂直距离为 ,当彼此交错时, 各抓住10m绳 绳 索的一端,然后相对旋转。 在抓住绳索一端之前, 索的一端,然后相对旋转。⑴ 在抓住绳索一端之前,各自对绳索中 心的角动量是多少?抓住之后是多少? 它们各自收拢绳索, 心的角动量是多少?抓住之后是多少?⑵ 它们各自收拢绳索,到绳 长为5m时 各自的速率如何? 绳长为5m时 绳内张力多大? 长为 时,各自的速率如何?⑶绳长为 时, 绳内张力多大?⑷二 人在收拢绳索时,各自做了多少功〉 总动能如何变化? 人在收拢绳索时,各自做了多少功〉⑸总动能如何变化? mv 设每个运动员的质量为m=70kg,收绳前相对 解:设每个运动员的质量为 , d 绳中心o的距离为 的距离为d 绳中心 的距离为 = d1= 5m,速率为 1=6.5m/s; ,速率为v=v ; o d 当把绳收拢为d 当把绳收拢为 = d2= 2.5m时, 速率 2 时 速率v=v mv 对绳中心o点的角动量各为 ⑴对绳中心 点的角动量各为 L=mv1d1=70×6.5×5=2275kgm2/s(抓住绳索前后角动量相同) × × (抓住绳索前后角动量相同) 在收绳过程中, ⑵把两个运动员视为一个质点系,在收绳过程中,质点系对 轴的角动 把两个运动员视为一个质点系 在收绳过程中 质点系对o轴的角动 量守恒,有 量守恒 有2m v1d1 = 2m v2 d2∴v2 = v1d1/d2 = 6.5×5/2.5 =13 m/s × 把某一运动员视为质点,作为研究对象,由牛顿第二定律, ⑶把某一运动员视为质点,作为研究对象,由牛顿第二定律,绳中张 力F = m v22/d2 = 70×132 /2.5 = 4732 N × ⑷由质点动能定理,每人所做的功均为: 由质点动能定理,每人所做的功均为: 2 2 A = 1 mv 2 − 1 mv 1 = 1 m(v 2 − v1 )(v 2 + v1 ) = 1 × 70(13 − 6.5)(13 + 6.5) = 4436J 2 2 2 2 ⑸总动能增大了∆Ek = 2×4436 = 8872 J 总动能增大了 ×
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例6.1
在半角为α的圆锥面内壁距顶角h的高
处,有一个小球以初速度v0沿内壁水平方向射
出。设锥面内壁光滑。
(1)为使小球在高h处的水平面上作匀速圆周 运动,v0=?; (2)若v1=2v0,求小球在运动过程中的最大高 度和最小高度(最大高度处沿内壁向速度为0)。
v0
N mg
h
1
r2 2
G M e Re Me G r 2 2r
4 r 2 8 Re r 3 Re 0
(5) (6)
r1
3 2
Re , r2 1 2
1 2
Re ( 舍 去 )
最大高度
h r1 R e
Re
例6.3 一质量为Ma、半径为a的圆筒A,被另一 质量为Mb、半径为b的圆筒B同轴套在其外,均 可自由转动。在圆筒A的内表面上散布了薄薄 的一层质量为Mo的沙子,并在壁上开了许多小 孔。在t=0时,圆筒A以角速度ω0 绕轴匀速 (不代表恒定角速度,即可变)转动,而圆 筒B静止。打开小孔,沙子向外飞出并附着于 B筒的内壁上。设单位时间内喷出的沙子质量 为k,若忽略沙子从A筒飞到B筒的时间,求t 时刻两筒旋转的角速度。
(3)
代入(1)式得
v v0 = 2 vc =
2 L
(4) (5)
代入(2)式得
2 L
球、杆合系统机械能守恒,有
1 2
2 m v0
L 2 2 2 m v + m vc + m 2 2 1
2 2 2 vc
2
即
2 v0
v +
+
1 2
L2 2
(6)
联立解得
a
b
【解】将圆筒A、沙子看作一个系统。由于对于转轴的 外力矩为零,对于轴的角动量不变。 在t时,角动量 在t+dt时,角动量
J t dt M a M 0 kt kdt a
2
2
J t M a M 0 kt a a
2
a d a kdta 2 a
J r1 m v1 r2 m v 2 2 r1 m v1
r v1, 1 v 2 v , r = L v 1 1
2 J J 2 m L v 2 m L sin
注意:J不是常矢量,其大小不变,但方向变化,绕竖直轴以 恒定角速度ω旋转。
令 dr/dt=0,得
2r
3
13 2
ar
2
9 2
a3 0 (9)
即
( r a )( r 3 a )(2 r
3 2
a) 0 (10)
由此得
r a , r 3a , r
3 4
a
最后一解不合解,舍去 。
例6.7 一根长为L的轻质刚性杆,其两端连着
1
2
,得到 (2)
2 Re
2 G M e r 2 r
抛体在在有心力场中运动,对地球中心角动量守
恒,即 可得
1 2
Re mv0 sin 60 mr 2
r
2
(3)
G M e Re 2r
2
G M e Re
或
2
(4)
代入(2)式 经整理得到 解得
G
Me 2 Re
2 2 2
M a M 0 kt a a kdta a
Ma
M 0 kt a d a ka dtd a kdta a
2
2 2
M a M 0 kt a a M a M 0 kt a d a
【解】采用极坐标系,则质点A、B的运动微分方程 分别为
m ( r 2 ) T mr 2 mh r (1) (2) T mg mr (3)
由(1)及(3),得
又由题所给条件,知
2 r 2 g r (4)
两个质量为m的质点,将此杆放在光滑的桌面
上,用一个质量为m,速度为v0 的质点与杆的
一端相碰。已知v0的方向与杆的夹角为45o,并 设为弹性碰撞。碰后,质点沿原直线返回。求 碰后杆的运动。
设碰撞时间为Δt,碰撞时平均作用力为F,碰后小
球返回的速度为V,杆作平面平行运动,其质心C点的 速度为Vc,杆的角速度为ω。 对小球,由动量定理,有
注意:J不是常矢量,其大小不变,但方向变化,绕竖直轴以 恒定角速度ω旋转。故此该系统被施以外力矩。 据角动量定理
M dJ dt
o 是J的单位矢量 J o o d J = J dt o o d d o M JJ = J J J J J dt dt 2 2 M M J cos 2 m L sin cos
2
gr c ( 7)
ga
代入(7)式,得
r2 1 h2 2 a 1
2
1 h2 2 r
2
gr ga
2a 2 r 2 ga 2 2a 2 r 2
( h 2 r 2 h 2 a 2 2 ga 2 r 3 2 ga 3 r 2 ) 9 3 13 2 ar a 2r 3 (8) 2 2
=
4
2
7L
v0
(7 )
代入(5)式,得 v c = 而
4 7
v0 1 7 v0
(8 )
v 2 vc v0 =
(9)
小球失去的动能为△Ek
Ek Ek Ek 0 1 48 1 48 2 mv mv ( m v0 ) Ek 0 2 2 49 2 49
2 0 2
1
习题(6)
可得:
b
a
2 2
kt
b kt M b
0
例6.4
两个质量均为m的质点,用一根长为2L
的轻杆相连。两质点以角速度ω绕轴转动,轴
线通过杆的中点O与杆的夹角为θ。试求以O为 参考点的质点组的角动量和所受的外力矩。
y
ω
L
v1
O L v2
J
x
【解】以O为参考点,两小球的位矢分别是:r1,r2。系统的角 动量为:
对于轴的角动量不变,则有 对照上两式则有
d a 0
J t J t dt
这说明A筒的角速度不变
a 0
将内筒B与附着的沙(包括即将附着的沙)视为一个系 统,对于转轴的外力矩为零,对于轴的角动量守恒。 在t时, 角动量: 在t+dt时, 角动量:
J t kt M b b b kdta 0
动。 机械能守恒,设上升得最大高度x,其速度为v2则
1 2
m v mg ( h x )
2 2
1 2
m v1 mgh
2
(3)
• 沿圆锥轴线得角动量分量守恒
htg mv1 ( h x )tg mv 2
2 h gh hx
(4)
上两式联立可得
v2
(5)
由(4)、(5)式得到 x3 − 3h2x=0
E0 1 2 mv G
2
0
M em Re
2 G M e m E mr r 2 r
2 2
1
(1)
在最高点
1 2 mv G
2
0
r 0
M em Re 1
,即有
2
2 G M e m mr 2 r
(1)’
代入
v0
G Me
GM e / R e
P152 3-13, 3-16,
3-19, 3-27, 3-28, 3-32
dt
d
o JJ
注意:M不是常矢量,其大小不变,但方向变化,绕竖直轴以பைடு நூலகம்恒定角速度ω旋转。
例6.5
小滑块A位于光滑的水平桌面上,小滑
块B位于桌面上的小槽中,两滑块的质量均为m,
并用长为L、不可伸长、无弹性的轻绳相连。
开始时,A、B之间的距离为L/2, A、B间的连
线与小槽垂直。突然给滑块A一个冲击,使其
α
α
x
v1
h
α
【解】 (1)小球受力:重力mg,约束反力N。小球的运 动方程
N sin mg N cos m v0
2
(1) m gh v
2 0
v0 r
2
htg
( 2) v 0= gh
() 2 得 tg = 1 ()
tg
(2) 当初速度v1=2v0时,平衡不成立。小球作螺旋运
) a 9 ga h r ( r 2
1 2
故
h
2
a
9 2
ga3 (5)
利用(2),将(4)式中的 消去,得到
2 r h2 r
3
g (6)
r2
1 h2
2
r a , r 0, c
2 r 1 h2 2 r
F t mv m ( v 0 ) m ( v v 0 ) (1)
m
对杆系统,有
F t 2 mv c (2)
c v0
L
45o
m
m
对于杆系统,相对质心C,由角动量定理,有
F t L 2 sin 45 L 2m 2
2
即有
F t
2 mL
