创新设计2016_2017学年高考数学第二章点直线平面之间的位置关系2.3.1直线与平面垂直的判定课时作业
《创新设计》2015-2016学年(人教版,必修二)高中数学第二章点、直线、平面之间的位置关系2.1.1

图形
符号
作用
一是判断两个
平面相交的依
P∈α,且 据;二是证明 P∈β⇒α∩β=l 点共线问题的
,且P∈l 依据; (3)证明线共点 问题的依据
课堂讲义
要点一 三种语言的转换 例 1 用符号语言表示下列语句,并画出图形.
(1)三个平面 α,β,γ 相交于一点 P,且平面 α 与平面 β 相 交于 PA,平面 α 与平面 γ 相交于 PB,平面 β 与平面 γ 相交 于 PC; (2)平面 ABD 与平面 BDC 相交于 BD,平面 ABC 与平面 ADC 相交于 AC.
A,B,C三点 不共线⇒存在 唯一的平面α 使A,B, C∈α
作用
既可判定直线 和点是否在平 面内,又能说 明平面是无限 延展的
一是确定平 面;二是证明 点、线共面问 题;三是判断 两个平面重合 的依据
预习导学
公理
内容
公理3
如果两个不重 合的平面有一 个公共点,那 么它们有且只 有一条_过__该__点_ _的__公__共__直__线___
直线l
__A_∉_l___ __A_∉_α__ __l⊂__α___
α∩β=l
预习导学
• 3.平面的基本性质及作用
公理 公理1
内容
如果一条直线 上的_两__点__在 一个平面内, 那么这条直线 在此平面内
公理2
过不在一条直 线上的三点, __有__且__只__有___ 一个平面
图形
符号
A∈l,B∈l, 且A∈α, B∈α⇒__l⊂__α_
高中数学·必修2 人教A版
第二章 点、直线、平面之间的位置关系
2.1 空间点、直线、平面之间的位置关系
2.1.1 平 面
高中数学 第二章 点、直线、平面之间的位置关系 2.2 直线与平面、平面与平面平行测试题(无答案)

山西省忻州市2016-2017学年高中数学第二章点、直线、平面之间的位置关系2.2 直线与平面、平面与平面平行测试题(无答案)新人教A版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(山西省忻州市2016-2017学年高中数学第二章点、直线、平面之间的位置关系2.2 直线与平面、平面与平面平行测试题(无答案)新人教A版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为山西省忻州市2016-2017学年高中数学第二章点、直线、平面之间的位置关系2.2 直线与平面、平面与平面平行测试题(无答案)新人教A版必修2的全部内容。
直线与平面、平面与平面平行本试卷满分70+5分一.选择题(每小题5分,共25分)1.若平面α和平面相交于直线L,直线a在平面α内但不与直线L重合,则直线a与平面的位置关系是 ( )A。
相交 B.平行C.相交或平行D. a在平面内2.在正方体ABCD—A1B1C1D1中,下列四对截面中彼此平行的一对截面是()A.面A1BC1和面ACD1 B。
面BDC1和面B1D1CC。
面B1D1D和面BDA D。
面A1DC1和面AD1C3.已知甲命题是“如果直线a∥b,那么a∥平面α”,乙命题是“如果a∥平面α,那么a∥b"。
使上面两个命题都成立,需分别添加的条件是 ( )A.甲:“b⊂α”,乙:“b⊂α”B.甲:“b⊂α”,乙:“a⊂β且α∩β=b"C。
甲:“aα,b⊂α”,乙:“a⊂β且α∩β=b”D.甲:“aα,b⊂α”,乙:“b∥α”4。
直线a∥平面,平面内有n条直线相交于一点,那么这n条直线中与直线a平行的( )A。
高中数学《第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系》845PPT课件

小结
(1)二面角的定义 ; (2)二面角平面角的定义;
利用二面角的平面角来刻画二面角的大小 (3)求解简单的二面角.
例 已知正方体 ABCD-A1B1C1D1 ,求 (3)二面角 C1-BD-C 的大小; (4)二面角 C1-BD-A 的大小.
例 已知正方体 ABCD-A1B1C1D1 ,求 (3)二面角 C1-BD-C 的大小; (4)二面角 C1-BD-A 的大小.
例 已知正方体 ABCD-A1B1C1D1 ,求 (3)二面角 C1-BD-C 的大小; (4)二面角 C1-BD-A 的大小.
例 已知正方体 ABCD-A1B1C1D1 ,求 (3)二面角 C1-BD-C 的大小; (4)二面角 C1-BD-A 的大小.
例 已知正方体 ABCD-A1B1C1D1 ,求 (3)二面角 C1-BD-C 的大小; (4)二面角 C1-BD-A 的大小.
例 已知正方体 ABCD-A1B1C1D1 ,求 (3)二面角 C1-BD-C 的大小; (4)二面角 C1-BD-A 的大小.
例 已知正方体 ABCD-A1B1C1D1 ,求 (1)二面角 A-BC-B1 的大小; (2)二面角 A-BC-D1 的大小;
例 已知正方体 ABCD-A1B1C1D1 ,求 (1)二面角 A-BC-B1 的大小; (2)二面角 A-BC-D1 的大小;
例 已知正方体 ABCD-A1B1C1D1 ,求 (1)二面角 A-BC-B1 的大小; (2)二面角 A-BC-D1 的大小;
定义:在二面角的棱 AB 上任取一点 O,
过 O 分别在面 和 上作棱 AB 的垂线
OM 和 ON,射线 OM 和 ON 所组成的
角叫做二面角 -AB- 的平面角.
高中数学《第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系》111PPT课件
A
A
(2)空间中线与线的位置关系
图形
b a
文字语言(读法)
两直线共面且无公 共点两直线平行
符号语言 a∥b
Ab a
两直线共面且有一个 aIb=A 公共点两直线相交
b a
两直线不共面且无 公共点两直线异面
a、b异面
(3)空间中线与面的位置关系
图形
a
文字语言(读法)
直线与平面无公共 点直线与平面平行
• ⑤用三种语言描述平面与平面之间的位置 关系.
两个平面的位置关系 有且只有两种:
位置关系 两平面平行
两平面相交
公共点 符号表示
没有公共点 α∥β
有一条公共直线
α∩β=a
图形表示
练习P50:1. 金版学案例题1, 2。 探究:思考?
2 如பைடு நூலகம்三个平面两两相交,那么它们的交线 有多少条?画出图形表示你的结论。 答:有可能1条,也有可能3条交线。
符号语言
a∥
a
A
直线与平面有一个公
共点直线与平面相交 aI =A
a 直线上所有的点都在
平面内直线在平面内
a
(4)空间中面与面的位置关系
图形
文字语言(读法)
符号语言
两个平面无公共点 两个平面平行
α∥β
β
两个平面有一公共直线 I l
α
两个平面相交
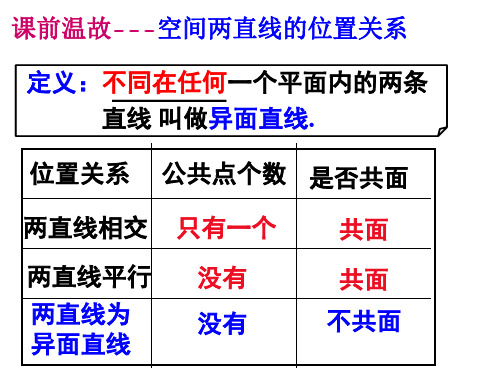
课前温故---空间两直线的位置关系
定义:不同在任何一个平面内的两条 直线 叫做异面直线.
位置关系 公共点个数 是否共面
两直线相交 只有一个 共面
两直线平行
两直线为 异面直线
没有 没有
共面 不共面
直线与平面的位置关系有且只有三种:
《创新设计》2015-2016学年(人教版,必修二)高中数学第二章点、直线、平面之间的位置关系2.3.2

预习导学
(2)画法:
记作:_α_⊥__β___. (3)面面垂直的判定定理 文字语言:一个平面过另一个平面的__垂__线___,则这两个平 面垂直.
预习导学
图形语言:如图所示
符号语言: a_⊥_二面角及其平面角的概念 • 例1 下列命题中: • ①两个相交平面组成的图形叫做二面角;
课堂讲义
跟踪演练 3 已知正四棱锥(底面为正方形各侧面为全等的 等腰三角形)的体积为 12,底面对角线的长为 2 6,求侧面 与底面所成的二面角. 解 设正四棱锥为 S-ABCD, 如图所示,高为 h,底面边长为 a, 则 2a2=(2 6)2, ∴a2=12. 又31a2h=12,∴h=3a62=3.
课堂讲义
设正方体的棱长为 a,
则 OB1= 22a,
在
Rt△BB1O
中,tan∠BOB1=OBBB11=
a= 2 2a
2,
所以二面角 B-A1C1-B1 的正切值为 2.
课堂讲义
•规律方法 1.求二面角的大小关键是要找出或 作出平面角.再把平面角放在三角形中,利用 解三角形得到平面角的大小或三角函数值,其 步骤为作角→证明→计算. •2.为在适当位置作出平面角要注意观察二面 角两个面的图形特点,如是否为等腰三角形 等.
• A.相等 B.互补 • C.相等或互补 D.关系无法确定
课堂讲义
• 答案 D • 解析 如图所示,平面EFDG⊥平面ABC,当
平面HDG绕DG转 • 动时,平面HDG始终与平面BCD垂直,所以两
个二面角的大小 • 关系不确定,因为二面角H-DG-F的大小不
确定.
课堂讲义
• 要点二 面面垂直的判定与证明 • 例2 如图,AB是⊙O的直径,
《创新设计》2015-2016学年(人教版,必修二)高中数学第二章点、直线、平面之间的位置关系2.2.3

课堂讲义
(2)若 AB、CD 异面, 如图,过 A 作 AE∥CD 交 α 于 E,取 AE 中点 P,连接 MP、 PN、BE、ED. ∵AE∥CD. ∴AE、CD 确定平面 AEDC. 则平面 AEDC 与 α、β 的交线分别为 ED、AC,∵α∥β,∴ ED∥AC.
课堂讲义
• 又P、N分别为AE、CD的中点, • ∴PN∥ED,又ED⊂平面α,PN⊄平面α,
课堂讲义
•规律方法 1.本题证明线面平行,利用了线面 平行的性质定理和判定定理进行转化,即线线 平行⇒线面平行⇒线线平行⇒线面平行. •2.在将线面平行转化为线线平行时,注意观 察图形中是否是性质定理中符合条件的平面.
课堂讲义 • 跟踪演练3 • 如图,三棱锥A-BCD被一平面所截,截面为
平行四边形 • EFGH.
系中,交替使用线线平行、线面平行的判定定理与性质定
理是解决此类问题的关键.
课堂讲义
• 跟踪演练1 若两个相交平面分别过两条平行 直线,则它们的
•解交已线知和:这a∥两b,条a⊂平α,行b直⊂β线,α平∩行β=.l.
求证:a∥b∥l. 证明:如图所示, ∵a∥b,b⊂β,a⊄β,∴a∥β, 又 a⊂α,α∩β=l,∴a∥l,又 a∥b, ∴a∥b∥l.
__平__面_内_______一条直线与此____________的 一条直线平行,则该直线与此平面两条平相行交.直线 • 2.平面与平面平行的判定定理:平面内的 ________________与另一个平面平行,则这 两个平面平行.
预习导学
• [预习导引]
线面平行的性质定理
面面平行的性质定理
文字
(•2)α解∩γ由=(1A)得C,ACβ∥∩BγD=,∴BDAPAB.又=CPαCD∥,∴β,45=∴C3DA,C∴∥CBDD=.145
完整版高中数学必修2《点、直线、平面之间位置关系》知识点
第二章点、直线、平面之间的位置关系空间点、直线、平面之间的位置关系一、平面1、平面及其表示A2、平面的根本性质①公理1:lBllAB②公理2:不共线的三点确定一个平面③公理3:Pl那么P lP二、点与面、直线位置关系1、A1、点与平面有2种位置关系2、B1、A l2、点与直线有2种位置关系2、B l三、空间中直线与直线之间的位置关系1、异面直线2、直线与直线的位置关系相交共面平行异面3、公理4和定理公理4:l1Pl3l1Pl2l2Pl3定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
4、求异面直线所成角的步骤:①作:作平行线得到相交直线; ②证:证明作出的角即为所求的异面直线所成的角;③构造三角形求出该角。
提示:1、作平行线常见方法有:直接平移,中位线,平行四边形。
2、异面直线所的角的范围是 00,900。
四、空间中直线与平面之间的位置关系位置关系 直线a 在平面内 直线a 与平面相交直线a 与平面 平行 公共点 有无数个公共点 有且只有一个公共点 没有公共点 符号表示a aI A aP 图形表示 五、空间中平面与平面之间的位置关系位置关系 两个平面平行 两个平面相交公共点 没有公共点有一条公共直线 符号表示 P I a图形表示直线、平面平行的判定及其性质一、线面平行1、判定:b a bPbPa〔线线平行,那么线面平行〕2、性质:aPaP abb〔线面平行,那么线线平行〕二、面面平行1、判定:aba b P PPbP〔线面平行,那么面面平行〕2、性质1:PI a aPbI b〔面面平行,那么线面平行〕性质2:PmPm〔面面平行,那么线面平行〕说明〔1〕判定直线与平面平行的方法:①利用定义:证明直线与平面无公共点。
②利用判定定理:从直线与直线平行等到直线与平面平行。
③利用面面平行的性质:两个平面平行,那么其中一个平面内的直线必平行于另一个平面。
2〕证明面面平行的常用方法利用面面平行的定义:此法一般与反证法结合。
高中数学《第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系》786PPT课件
例 1:正方形 ABCD 与正方形 ABEF 所在平面相交于 AB, 在 AE、BD 上各有一点 P、Q,且 AP=DQ. 求证:PQ∥平面 BCE.
证明 方法一 如图所示. 作 PM∥AB 交 BE 于 M,作 QN∥AB 交 BC 于 N,连接 MN. ∵正方形 ABCD 和正方形 ABEF 有公共边 AB,∴AE=BD. 又 AP=DQ,∴PE=QB, 又 PM∥AB∥QN,∴PAMB=APEE=QBDB=QDNC,∴PAMB=QDNC,
证明线面平行的关键点及探求线线平行的方法 (1)证明直线与平面平行的关键是设法在平面内找到 一条与已知直线平行的直线; (2)利用几何体的特征,合理利用中位线定理、线面 平行的性质,或者构造平行四边形、寻找比例式证明两 直线平行; (3)注意说明已知的直线不在平面内,即三个条件缺 一不可.
判定面面平行的方法 (1)利用定义:即证两个平面没有公共点(不常用); (2)利用面面平行的判定定理(主要方法); (3)利用垂直于同一条直线的两平面平行(客观题可用); (4)利用平面平行的传递性,即两个平面同时平行于第三 个平面,则这两个平面平行(客观题可用).
第四 节
直线、平面平行的判定及其性质
1.直线与平面平行的判定定理和性质定理
文字语言
பைடு நூலகம்
图形语言
判 平面外一条直线与 此平面内 的 定
一条直线平行,则该直线与此平 定
面平行(线线平行⇒线面平行) 理
性 一条直线与一个平面平行,则过
质 这条直线的任一平面与此平面的 定 交线 与该直线平行(简记为“线
理 面平行⇒线线平行”)
作业
1.预习8.5节; 2.《乐学七中一轮》活页8.4节; 3.错题整理
符号语言
(完整版)高中数学必修2《点、直线、平面之间的位置关系》知识点
第二章点、直线、平面之间的地址关系空间点、直线、平面之间的地址关系一、平面1、平面及其表示2、平面的基本性质①公义 1:A lB llAB②公义 2:不共线的三点确定一个平面③公义 3:Pl 则P lP二、点与面、直线地址关系1、A1、点与平面有 2 种地址关系2、B1、A l2、点与直线有 2 种地址关系2、 B l三、空间中直线与直线之间的地址关系1、异面直线2、直线与直线的地址关系订交共面平行异面3、公义 4 和定理公义 4:l1 Pl3l1 Pl 2l 2 Pl3定理:空间中若是两个角的两边分别对应平行,那么这两个角相等或互补。
4、求异面直线所成角的步骤:① 作:作平行线获取订交直线;② 证:证明作出的角即为所求的异面直线所成的角;③ 构造三角形求出该角。
提示: 1、作平行线常有方法有:直接平移,中位线,平行四边形。
2、异面直线所的角的范围是00 ,900。
四、空间中直线与平面之间的地址关系地址关系直线 a在平面内直线 a与平面订交直线 a与平面平行公共点有无数个公共点有且只有一个公共点没有公共点符号表示a a I Aa P图形表示五、空间中平面与平面之间的地址关系地址关系两个平面平行两个平面订交公共点没有公共点有一条公共直线符号表示P I a图形表示直线、平面平行的判断及其性质一、线面平行1、判断:ba b Pb Pa(线线平行,则线面平行)2、性质:a PaPa b b(线面平行,则线线平行)二、面面平行1、判断:aba b P Pa Pb P(线面平行,则面面平行)2、性质 1:PI a a PbI b(面面平行,则线面平行)性质 2:Pm Pm(面面平行,则线面平行)说明( 1)判断直线与平面平行的方法:① 利用定义:证明直线与平面无公共点。
② 利用判判定理:从直线与直线平行等到直线与平面平行。
③ 利用面面平行的性质:两个平面平行,则其中一个平面内的直线必平行于另一个平面。
(2)证明面面平行的常用方法①利用面面平行的定义:此法一般与反证法结合。
高中数学《第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系》778PPT课件
1、AC和DD1所成角是 90 度
2、AC和D1C1所成角是 45 度
3、AC和B1D1所成角是 90 度
4、AC和A1B所成角是 60 度
5、O为B1D1中点,AC和BO所成的角是 90 度
6、A1D1与AB的距离是 a
.
ห้องสมุดไป่ตู้ 知识总结
试一试 4.
正方体ABCD-A1B1C1D1中,
异面直线AC与B1C1所成的角为 .
D1
C1
45°
A1
B1
D A
C B
试一试:
5、如图所示:正方体的棱所在的直线
中,与直线A1B异面的有哪些?
D1 A1
C1 B1
D1C1、CD、
D1D、 C1C、
D
C
AD、B1C1
A
B
试一试: 设正方体的棱长为a ,
有且只有一个 没有 没有
2、空间两条直线的位置关系
(2)平行公理 公理4:平行于同一直线的两条直 线 互相平行——空间平行线的传递性.
(3)等角定理 空间中如果两个角的两边分别 对应平行,那 么这两个角相等或互补.
3、直线和平面的位置关系
直线在平面内 直线与平面相交 直线与平面平行
4、平面与平面的位置关系
两平面平行
两平面相交
探究: 已知平面, ,直线a, b,且∥,
a, b,则直线a与直线b具有怎样的位置关系?
试一试:
1.分别在两个平面内的两条直线的
位置关系是( D )
A.异面
B.平行
C.相交
D.以上都有可能
试一试
2.已知a,b是异面直线,直线c∥直线a,
则c与b( C)
A.一定是异面直线 B.一定是相交直线 C.不可能是平行直线 D.不可能是相交直线
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§2.3直线、平面垂直的判定及其性质
2.3.1直线与平面垂直的判定
【课时目标】1.掌握直线与平面垂直的定义.2.掌握直线与平面垂直的判定定理并能灵活应用定理证明直线与平面垂直.3.知道斜线在平面上的射影的概念,斜线与平面所成
角的概念.
1.直线与平面垂直
(1)定义:如果直线l 与平面α内的________________直线都________,就说直线l 与平面α互相垂直,记作________.直线l 叫做平面α的________,平面α叫做直线l 的________.
(2)判定定理
文字表述:一条直线与一个平面内的________________________都垂直,则该直线与此平面垂直.
符号表述:
l ⊥α.
2.直线与平面所成的角(1)
定义:平面的一条斜线和它在平面上的________所成的________,叫做这条直线和这个平面所成的角.
如图所示,________就是斜线AP 与平面α所成的角.
(2)当直线AP 与平面垂直时,它们所成的角的度数是90°;
当直线与平面平行或在平面内时,它们所成的角的度数是________;线面角θ的范围:________.
一、选择题
1.下列命题中正确的个数是()
①如果直线l 与平面α内的无数条直线垂直,则l ⊥α;②如果直线l 与平面α内的一条直线垂直,则l ⊥α;③如果直线l 不垂直于α,则α内没有与l 垂直的直线;
④如果直线l 不垂直于α,则α内也可以有无数条直线与l 垂直.A.0B.1C.2D.3
2.直线a ⊥直线b ,b ⊥平面β,则a 与β的关系是()A.a ⊥βB.a ∥β
C.a ⊂βD.a ⊂β或a ∥β
3.空间四边形ABCD 的四边相等,则它的两对角线AC 、BD 的关系是()
A.垂直且相交B.相交但不一定垂直
C.垂直但不相交D.不垂直也不相交
4.如图所示,定点A 和B 都在平面α内,定点P ∉α,PB ⊥α,C 是平面α内异于A 和B 的动点,且PC ⊥AC ,则△ABC 为()
A.锐角三角形B.直角三角形C.钝角三角形D.无法确定
5.如图所示,PA ⊥平面ABC ,△ABC 中BC ⊥AC ,则图中直角三角形的个数为()
A.4B.3C.2D.1
6.从平面外一点向平面引一条垂线和三条斜线,斜足分别为A ,B ,C ,如果这些斜线与平面成等角,有如下命题:
①△ABC 是正三角形;②垂足是△ABC 的内心;③垂足是△ABC 的外心;④垂足是△ABC 的垂心.其中正确命题的个数是()A.1B.2C.3D.4二、填空题
7.在正方体ABCD -A 1B 1C 1D 1中,
(1)直线A 1B 与平面ABCD 所成的角是________;(2)直线A 1B 与平面ABC 1D 1所成的角是________;(3)直线A 1B 与平面AB 1C 1D 所成的角是________.8.在直三棱柱ABC —A 1B 1C 1中,BC =CC 1,当底面A 1B 1C 1满足条件________时,有AB 1⊥BC 1(注:填上你认为正确的一种条件即可,不必考虑所有可能的情况).
9.如图所示,在正方体ABCD -A 1B 1C 1D 1中,M 、N 分别是棱AA 1和AB 上的点,若∠B 1MN 是直角,则∠C 1MN =________.
三、解答题
10.如图所示,在正方体ABCD —A 1B 1C 1D 1中,E 、F 分别是棱B 1C 1、B 1B 的中点.求证:CF ⊥平面EAB .
11.如图所示,在四棱锥P —ABCD 中,底面ABCD 是矩形,侧棱PA 垂直于底面,E 、F 分别是AB ,PC 的中点,PA =AD .
求证:(1)CD ⊥PD ;(2)EF ⊥平面PCD .
能力提升
12.如图所示,在正方体ABCD -A 1B 1C 1D 1中,P 为DD 1的中点,O 为ABCD 的中心,求证B 1O ⊥平面PAC .
13.如图所示,△ABC 中,∠ABC =90°,SA ⊥平面ABC ,过点A 向SC 和SB 引垂线,垂足分别是P 、Q ,求证:(1)AQ ⊥平面SBC ;
(2)PQ ⊥SC .
1.运用化归思想,将直线与平面垂直的判定转化为直线与平面内两条相交直线的判定,而同时还由此得到直线与直线垂直.即“线线垂直⇔线面垂直”.
2.直线和平面垂直的判定方法
(1)利用线面垂直的定义.
(2)利用线面垂直的判定定理.
(3)利用下面两个结论:
①若a∥b,a⊥α,则b⊥α;
②若α∥β,a⊥α,则a⊥β.
3.线线垂直的判定方法
(1)异面直线所成的角是90°.
(2)线面垂直,则线线垂直.
§2.3直线、平面垂直的判定及其性质
2.3.1直线与平面垂直的判定
答案
知识梳理
1.(1)任意一条垂直l⊥α垂线垂面
(2)两条相交直线a⊂αb⊂αa∩b=A
2.(1)射影锐角∠PAO
(2)0°[0°,90°]
作业设计
1.B[只有④正确.]
2.D
3.C[取BD中点O,连接AO,CO,
则BD⊥AO,BD⊥CO,
∴BD⊥面AOC,BD⊥AC,
又BD、AC异面,∴选C.]
4.B[易证AC⊥面PBC,所以AC⊥BC.]
5.A[PA⊥平面ABC
BC⊂平面ABC
PA⊥BC
AC⊥BC
⇒BC⊥平面PAC⇒BC⊥PC,
∴直角三角形有△PAB、△PAC、△ABC、△PBC.] 6.A[PO⊥面ABC.
则由已知可得,△PAO、△PBO、△PCO全等,
OA=OB=OC,
O为△ABC外心.
只有③正确.]
7.(1)45°(2)30°(3)90°
解析
(1)由线面角定义知∠A 1BA 为A 1B 与平面ABCD 所成的角,∠A 1BA=45°.(2)连接A 1D、AD 1,交点为O,
则易证A 1D⊥面ABC 1D 1,所以A 1B 在面ABC 1D 1内的射影为OB,∴A 1B 与面ABC 1D 1所成的角为∠A 1BO,
∵A 1O=1
2
A 1B,
∴∠A 1BO=30°.
(3)∵A 1B⊥AB 1,A 1B⊥B 1C 1,
∴A 1B⊥面AB 1C 1D,即A 1B 与面AB 1C 1D 所成的角为90°.8.∠A 1C 1B 1=90°解析
如图所示,连接B 1C,
由BC=CC 1,可得BC 1⊥B 1C,
因此,要证AB 1⊥BC 1,则只要证明BC 1⊥平面AB 1C,
即只要证AC⊥BC 1即可,由直三棱柱可知,只要证AC⊥BC 即可.因为A 1C 1∥AC,B 1C 1∥BC,故只要证A 1C 1⊥B 1C 1即可.(或者能推出A 1C 1⊥B 1C 1的条件,如∠A 1C 1B 1=90°等)9.90°
解析∵B 1C 1⊥面ABB 1A 1,∴B 1C 1⊥MN.又∵MN⊥B 1M,∴MN⊥面C 1B 1M,∴MN⊥C 1M.
∴∠C 1MN=90°.
10.证明在平面B 1BCC 1中,∵E、F 分别是B 1C 1、B 1B 的中点,∴△BB 1E≌△CBF,∴∠B 1BE=∠BCF,
∴∠BCF+∠EBC=90°,∴CF⊥BE,又AB⊥平面B 1BCC 1,CF ⊂平面B 1BCC 1,∴AB⊥CF,AB∩BE=B,∴CF⊥平面EAB.11.证明(1)∵PA⊥底面ABCD,∴CD⊥PA.
又矩形ABCD 中,CD⊥AD,且AD∩PA=A,∴CD⊥平面PAD,∴CD⊥PD.
(2)取PD 的中点G,连接AG,FG.又∵G、F 分别是PD,PC 的中点,
∴GF 綊1
2
CD,∴GF 綊AE,
∴四边形AEFG 是平行四边形,∴AG∥EF.
∵PA=AD,G 是PD 的中点,∴AG⊥PD,∴EF⊥PD,
∵CD⊥平面PAD,AG ⊂平面PAD.∴CD⊥AG.∴EF⊥CD.
∵PD∩CD=D,∴EF⊥平面PCD.
12.证明连接AB 1,CB 1,设AB=1.∴AB 1=CB 1=2,
∵AO=CO,∴B 1O⊥AC.连接PB 1.
∵OB 21=OB 2
+BB 21=32,
PB 21=PD 21+B 1D 2
1=94,
OP 2=PD 2+DO 2
=34
,
∴OB 21+OP 2=PB 2
1.∴B 1O⊥PO,又∵PO∩AC=O,∴B 1O⊥平面PAC.
13.证明(1)∵SA⊥平面ABC,BC ⊂平面ABC,∴SA⊥BC.
又∵BC⊥AB,SA∩AB=A,∴BC⊥平面SAB.又∵AQ ⊂平面SAB,
∴BC⊥AQ.又∵AQ⊥SB,BC∩SB=B,∴AQ⊥平面SBC.
(2)∵AQ⊥平面SBC,SC ⊂平面SBC,∴AQ⊥SC.
又∵AP⊥SC,AQ∩AP=A,
∴SC⊥平面APQ.∵PQ ⊂平面APQ,∴PQ⊥SC.。
