高仿真直线一级倒立摆模型设计

合集下载

自动化实验-倒立摆实验-附仿真结果图

一、直线一级倒立摆的仿真(一)直线一级倒立摆的数学建模对于倒立摆系统，由于其本身是自不稳定的系统,实验建模存在一定的困难。

但是忽略掉一些次要的因素后，倒立摆系统就是一个典型的运动的刚体系统，可以在惯性坐标系内应用经典力学理论建立系统的动力学方程。

下面我们采用其中的牛顿－欧拉方法和拉格朗日方法分别建立直线型一级倒立摆系统的数学模型.图2 直线一级倒立摆模型φ摆杆与垂直向上方向的夹角；θ摆杆与垂直向下方向的夹角（考虑到摆杆初始位置为竖直向下）。

图3 小车及摆杆受力分析分析小车水平方向所受的合力，可以得到以下方程:由摆杆水平方向的受力进行分析可以得到下面等式:把这个等式代入式1中,就得到系统的第一个运动方程：为了推出系统的第二个运动方程，我们对摆杆垂直方向上的合力进行分析,可以得到下面方程:力矩平衡方程如下：注意：此方程中力矩的方向,由于θ=π+φ,cosφ= −cosθ,sinφ= −sin θ，故等式前面有负号。

合并这两个方程，约去P 和N，得到第二个运动方程:设θ=π+φ(φ是摆杆与垂直向上方向之间的夹角），假设φ与1（单位是弧度）相比很小，即φ<〈1，则可以进行近似处理:。

用u 来代表被控对象的输入力F，线性化后两个运动方程如下:对式9进行拉普拉斯变换，得到注意：推导传递函数时假设初始条件为0。

由于输出为角度φ，求解方程组的第一个方程，可以得到：或如果令v = x，则有：把上式代入方程组的第二个方程，得到：整理后得到传递函数：其中设系统状态空间方程为:方程组对解代数方程,得到解如下：整理后得到系统状态空间方程：设则有：实际系统的模型参数如下:M 小车质量1。

096 Kgm 摆杆质量0.109 Kgb 小车摩擦系数0 。

1N/m/secl 摆杆转动轴心到杆质心的长度0。

2 5mI 摆杆惯量0。

0034 kg＊m*m把上述参数代入，可以得到系统的实际模型。

摆杆角度和小车位移的传递函数:摆杆角度和小车加速度之间的传递函数为：摆杆角度和小车所受外界作用力的传递函数：以外界作用力作为输入的系统状态方程:(二)倒立摆的PID调节：经典控制理论的研究对象主要是单输入单输出的系统，控制器设计时一般需要有关被控对象的较精确模型。

(完整版)一级倒立摆系统分析

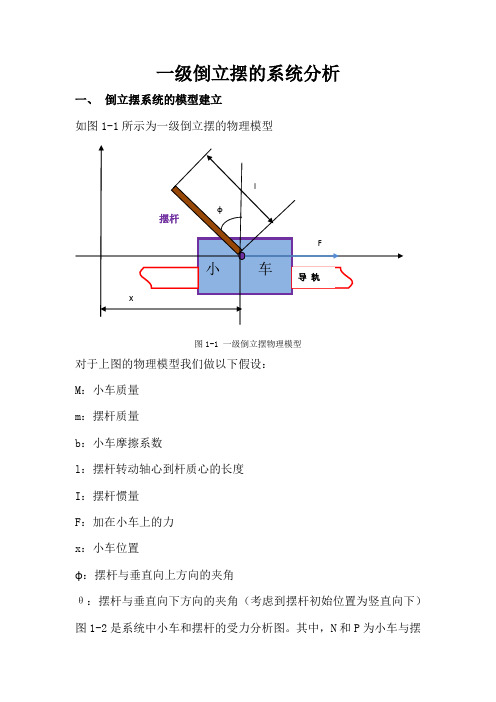
一级倒立摆的系统分析一、倒立摆系统的模型建立如图1-1所示为一级倒立摆的物理模型图1-1 一级倒立摆物理模型对于上图的物理模型我们做以下假设：M：小车质量m：摆杆质量b：小车摩擦系数l：摆杆转动轴心到杆质心的长度I：摆杆惯量F：加在小车上的力x：小车位置ɸ：摆杆与垂直向上方向的夹角θ：摆杆与垂直向下方向的夹角（考虑到摆杆初始位置为竖直向下）图1-2是系统中小车和摆杆的受力分析图。

其中，N和P为小车与摆杆相互作用力的水平和垂直方向的分量。

注意：实际倒立摆系统中的检测和执行装置的正负方向已经完全确定，因而矢量方向定义如图所示，图示方向为矢量正方向。

图1-2 小车及摆杆受力分析分析小车水平方向受力，可以得到以下方程：M ẍ＝Ｆ-ｂẋ-Ｎ (1-1)由摆杆水平方向的受力进行分析可以得到以下方程：N =md 2dt 2(x +l sin θ) (1-2)即： N =mẍ+mlθcos θ−mlθ2sin θ (1-3)将这个等式代入式（1-1）中，可以得到系统的第一个运动方程： (M +m )ẍ+bẋ+mlθcos θ−mlθ2sin θ=F (1-4)为推出系统的第二个运动方程，我们对摆杆垂直方向上的合力进行分析，可以得出以下方程： P −mg =md 2dt 2(l cos θ) (1-5)P −mg =− mlθsin θ−mlθ2cos θ (1-6) 利用力矩平衡方程可以有：−Pl sinθ−Nl cosθ=Iθ (1-7)注意：此方程中的力矩方向，由于θ=π+ɸ，cosɸ=−cosθ，sinɸ=−sinθ，所以等式前面含有负号。

合并两个方程，约去P和N可以得到第二个运动方程：(I+ml2)θ+mgl sinθ=−mlẍcosθ (1-8)设θ=π+ɸ，假设ɸ与1（单位是弧度）相比很小，即ɸ＜＜1，则可以进行近似处理：cosθ=−1，sinθ=−ɸ，（dθdt ）2=0。

用u来代表被控对象的输入力F，线性化后的两个运动方程如下：{(I+ml2)ɸ−mglɸ=mlẍ(M+m)ẍ+bẋ−mlɸ=u(1-9)假设初始条件为0，则对式（1-9）进行拉普拉斯变换，可以得到：{(I+ml2)Φ(s)s2−mglΦ(s)=mlX(s)s2(M+m)X(s)s2+bX(s)s−mlΦ(s)s2=U(s) (1-10) 由于输出为角度ɸ，求解方程组的第一个方程，可以得到：X(s)=[(I+ml2)ml −gs2]Φ(s) (1-11)或改写为：Φ(s)X(s)=mls2(I+ml2)s2−mgl(1-12)如果令v=ẍ,则有：Φ(s)V（s）=ml(I+ml2)s2−mgl(1-13)如果将上式代入方程组的第二个方程，可以得到：(M+m)[(I+ml2)ml −gs]Φ(s)s2+b[(I+ml2)ml+gs2]Φ(s)s−mlΦ(s)s2=U(s) (1-14) 整理后可得传递函数：Φ(s) U(s)=mlqs2s4+b(I+ml2)qs3−(M+m)mglqs2−bmglqs(1-15)其中q=[(M+m)(I+ml2)−(ml)2]假设系统状态空间方程为：X=AX+Buy=CX+Du (1-16) 方程组对ẍ,ɸ解代数方程，可以得到解如下：{ẋ=ẋẍ=−(I+ml2)bI(M+m)+Mml2ẋ+m2gl2I(M+m)+Mml2ɸ+(I+ml2)I(M+m)+Mml2uɸ=ɸɸ=−mlbI(M+m)+Mml2ẋ+mgl(M+m)I(M+m)+Mml2ɸ+mlI(M+m)+Mml2u(1-17)整理后可以得到系统状态空间方程：[ẋẍɸɸ]=[01000−(I+ml2)bI(M+m)+Mml2m2gl2I(M+m)+Mml200010−mlbI(M+m)+Mml2mgl(M+m)I(M+m)+Mml20][xẋɸɸ]+[(I+ml2)I(M+m)+Mml2mlI(M+m)+Mml2]uy=[xɸ]=[10000010][xẋɸɸ]+[0]u(1-18)由（1-9）的第一个方程为：(I+ml2)ɸ−mgl ɸ=mlẍ对于质量均匀分布的摆杆可以有：I=13ml2于是可以得到：(13ml2+ml2)ɸ−mgl ɸ=mlẍ化简可以得到：ɸ=3g4l ɸ+34lẍ(1-19)设X={x, ẋ, ɸ , ɸ}，u=ẍ则有：[ẋẍɸɸ]=[010000000001003g4l0][xẋɸɸ]+[134l]uy=[xɸ]=[10000010][xẋɸɸ]+[0]u(1-20)以上公式推理是根据牛顿力学的微分方程验证的。

(完整word版)一级倒立摆的Simulink仿真

单级倒立摆稳定控制直线-级倒立摆系统在忽略了空'(阻力及各种摩擦Z后，町抽象成小车和匀质摆杆组成的系统，如图1所示。

图2控制系统结构假设小车质量M=0.5kg,匀质摆朴质量m=0.2kg,摆朴长度21 =0.6m, x(t)为小车的水半位移，〃为摆杆的角位移，g = 9.8m/s2o控制的目标是通过外力u⑴使得摆直立向上(即&(t) = 0) o该系统的非线性模型为:(J +inl‘)典(nilcos^)&= niglsin^ (ml cos。

)翼(M其中J二一ml+ m)&= (mlsin0)6^ + u一、非线性模型线性化及建立状态空间模型因为在工作点附近(& = 0.必0)对系统进行线竹:•化，所以可以做如下线性化处理: 03 Q1sin0« 0 --------- 、COS&Q 1-----------------3! 2!当e很小时，由COS0V sine的幕级数展开式可知，忽略高次项后, 可得cos0~l, sin0=0, 0Z 2=0：因此模型线性化后如下：(J+nil A2)0r z +mlx z z =mgl0 (a)取系统的状态变量为％ = x,x2 =仪X3 = x4=灰输出y = [x OF包扌舌小车位移和摆杆的角位移.由线性化后运动方程组得故空间状态方程如下:■010 0 ■「xT■ ■x2*00-2.6727 0x21 1.8182 x3f =000 1x3+0_x4J|_x40031.1818 0-4.5455uml0f r + (M+m) x''二u (b) 其中J = -ml3■ ■ xl ■ ■Xx2x1 x30 x4&Y=xlx3X1/二x'=x2—沁—册4(M + m) 一3m44(M + m) - 3m u3(M +m)g4(M + m)l 一3ni-34(M + m)l 一311119 1 00 ''xlM00 -3mg0am xl x2‘ _4(M + m) 一3m x2 x3* ~00 01x3x4J00 3(M + m)g0[_x44(M + m)l - 3ml 044(M + m) - 3m 0一34(M + m)l - 3nil二. 通过Matlab 仿真判断系统的可控与可观性，并说明其物理意义。

直线一级摆的极点配置及仿真.

内蒙古科技大学控制系统仿真课程设计说明书题目：直线一级摆的极点配置及仿真学生姓名：丛伟学号：0967112316专业：测控技术与仪器班级：测控09-3班指导教师：张勇为实现多输入、多输出、高度非线不稳定的倒立摆系统平衡稳定控制，将倒立摆系统的非线性模型进行近似线性化处理，获得系统在平衡点附近的线性化模型。

利用牛顿—欧拉方法建立直线型一级倒立摆系统的数学模型。

在分析的基础上，基于状态反馈控制中极点配置法对直线型倒立摆系统设计控制器。

由MATLAB 仿真表明采用的控制策略是有效的，设计的控制器对直线型一级倒立摆系统的平衡稳定性效果好，提高了系统的干扰能力。

关键词：倒立摆、极点配置、MATLAB仿真引言 (1)第一章 Matlab及Simulink简介 (2)1.1 Matlab简介 (2)1.2 Simulink简介 (2)第二章设计目的及要求 (4)第三章直线一阶倒立摆简介 (5)3.1 一阶倒立摆简介 (5)第四章数学模型的建立 (6)4.1 数学模型的建立 (6)4.1.1微分方程的数学模型 (6)4.1.2状态空间数学模型 (8)4.2 系统稳定性分析 (10)4.3 系统可控性分析 (11)第五章状态空间极点配置 (13)5.1 状态空间分析 (13)5.2 状态空间极点配置 (14)第六章仿真验证 (18)6.1 Simulink仿真程序图及参数设置 (18)6.1.1 Simulink仿真参数设置 (18)6.2 仿真图形 (20)第七章总结 (21)参考文献 (22)倒立摆是进行控制理论研究的典型实验平台。

由于倒立摆系统的控制策略和杂技运动员顶杆平衡表演的技巧有异曲同工之处，极富趣味性，而且许多抽象的控制理论概念如系统稳定性、可控性和系统抗干扰能力等等，都可以通过倒立摆系统实验直观的表现出来，因此在欧美发达国家的高等院校，它已成为必备的控制理论教学实验设备。

学习自动控制理论的学生通过倒立摆系统实验来验证所学的控制理论和算法，非常的直观、简便，在轻松的实验中对所学课程加深了理解。

一级倒立摆的Simulink仿真

一级倒立摆的Simulink仿真第一篇：一级倒立摆的Simulink仿真单级倒立摆稳定控制直线一级倒立摆系统在忽略了空气阻力及各种摩擦之后，可抽象成小车和匀质摆杆组成的系统，如图1所示。

杆长为2λmguθ图1 直线一级倒立摆系统图2 控制系统结构假设小车质量M =0.5kg，匀质摆杆质量m=0.2kg，摆杆长度2l =0.6m，x(t)为小车的水平位移，θ为摆杆的角位移，g=9.8m/s2。

控制的目标是通过外力u(t)使得摆直立向上（即θ(t)=0）。

该系统的非线性模型为：&&+(mlcosθ)&12&=mglsinθ(J+ml2)θxJ=ml。

，其中2&&&3&=(mlsinθ)θ+u(mlcosθ)θ+(M+m)&x解：一、非线性模型线性化及建立状态空间模型&=0）对系统进行线性化，所以因为在工作点附近（θ=0,θsinθ≈θ-θ33!可以做如下线性化处理：,cosθ≈1-θ22!当θ很小时，由cosθ、sinθ的幂级数展开式可知，忽略高次项后，可得cosθ≈1，sinθ≈θ，θ’^2≈0；因此模型线性化后如下：（J+ml^2）θ’’+mlx’’=mglθ(a)mlθ’’+(M+m)x’’=u(b)其中J=ml13&,输出y=[x&,x3=θ,x4=θ取系统的状态变量为x1=x,x2=x的角位移.θ]T包括小车位移和摆杆⎡x1⎤⎡x⎤⎢x2⎥⎢x'⎥⎡x⎤⎡x1⎤即X=⎢⎥=⎢⎥ Y=⎢⎥=⎢⎥⎢x3⎥⎢θ⎥⎣θ⎦⎣x3⎦⎢⎥⎢⎥⎣x4⎦⎣θ'⎦由线性化后运动方程组得-3mg4X1’=x’=x2 x2’=x’’=x3+u4(M+m)-3m4(M+m)-3m3(M+m)g-3X3’ =θ’=x4 x4’=θ’’=x3+u4(M+m)l-3ml4(M+m)l-3ml故空间状态方程如下：⎡0⎢⎡x1'⎤⎢0⎢x2'⎥⎢X’=⎢⎥=⎢⎢x3'⎥⎢0⎢⎥⎢⎣x4'⎦⎢0⎣100⎤⎡0⎤⎥⎢⎥-3mgx14⎡⎤⎢⎥00⎥⎢⎥4(M+m)-3m⎥x2⎢4(M+m)-3m⎥⎢⎥+ ⎢⎥001⎥0⎥⎢x3⎥⎢⎥⎢⎥⎥x4⎢⎥3(M+m)g-300⎥⎣⎦⎢⎥4(M+m)l-3ml⎦⎣4(M+m)l-3ml ⎦u⎡x1'⎤⎡0⎢x2'⎥⎢0⎢⎥⎢X’=⎢x3'⎥=⎢⎥⎢0⎣x4'⎦⎢⎣0100⎤0⎡⎤x1⎡⎤⎢1.8182⎥⎢x2⎥0-2.67270⎥⎥⎢⎥ + ⎢⎥ ux3⎥001⎥⎢⎢0⎥⎢⎥⎥⎣x4⎦⎢⎥031.18180⎦⎣-4.5455⎦⎡x1⎤⎢⎥⎡x1⎤⎡1000⎤⎢x2⎥Y= ⎢⎥=⎢⎥⎢⎥⎣x3⎦⎣0010⎦x3⎢⎥⎣x4⎦二、通过Matlab仿真判断系统的可控与可观性，并说明其物理意义。

直线一级倒立摆建模与控制

期望特征多项式为
s 2 k2 20 s 20 k1 k2 1
* 由设计者选取，考虑“引入状态反馈向量后系统特 1*、2
* f * s s 1* s 2 =s2 (1* 2* )s 1*2*
征多项式”和“期望特征多项式”的系数相等即可求出状态反馈向量。
，线性化运动方程。
倒立摆系统单输入-单输出传递函数模型
线性化后运动方程（参考）：
I ml mgl mlx
2
以小车加速度为输入、摆杆角度为输出，令
ax
拉普拉斯变换后系统传递函数模型（参考）：
s ml G s A s I ml 2 s 2 mgl
双击“Controller1”，输入选取的4个闭环极点对应的增益，运行仿真后双击 “Scope1”观测响应曲线，其中小车位置应该很好的收敛到0.01，小车速度、摆杆角
度和角速度应该收敛到0。若响应曲线效果不好则需重新选取闭环极点。
状态空间极点配置实物控制
选取了合适的4个闭环极点并通过了仿真测试后即可进行倒立摆系统实物控制。进入 MATLAB Simulink 实时控制工具箱“Googol Education Products”打开 “Inverted Pendulum\Linear Inverted Pendulum\Linear 1-Stage IP Swing-Up Control”中的“Swing-Up Control Demo，如下图。
状态空间极点配置仿真控制
参考上述实例，选取倒立摆系统的4个闭环极点，进入 MATLAB Simulink 实时控制工具箱“Googol Education Products”打开“Inverted Pendulum\Linear Inverted Pendulum\Linear 1-Stage IP Experiment\ Poles Placement Experiments”中的“Poles Control Simulink”，如下图。

直线一级倒立摆的建模及性能分析

直线一级倒立摆的建模及性能分析1 直线一级倒立摆数学模型的成立 (1)2 直线一级倒立摆系统的实际模型 (5)3 直线一级倒立摆系统的性能分析 (6)相关理论的介绍 (6)倒立摆系统的性能分析 (7)1 直线一级倒立摆数学模型的成立所谓系统的数学模型，是指利用数学结构来反映实际系统内部之间、系统内部与外部某些要紧相关因素之间的精准的定量表示。

数学模型是分析、设计、预测和操纵一个系统的理论基础。

因此，关于实际系统的数学模型的成立就显得尤其重要。

系统数学模型的构建能够分为两种：实验建模和机理建模。

实验建模确实是通过在研究对象上加上一系列的研究者事前确信的输入信号，鼓励研究对像并通过传感器检测其可观测的输出，应用数学手腕成立起系统的输入－输出关系。

机理建模确实是在了解研究对象的运动规律的基础上，通过物理、化学的知识和数学手腕成立起系统内部的输入－状态关系。

关于倒立摆系统，由于其本身是不稳固的系统，无法通过测量频率特性的方法获取其数学模型，实验建模存在必然的困难。

可是通过警惕的假设忽略掉一些次要的因素后，倒立摆系统是一个典型的机电一体化系统，其机械部份遵守牛顿运动定律，其电子部份遵守电磁学的大体定律，因此能够通过机理建模取得系统较为精准的数学模型。

为了简单起见，在建模时忽略系统中的一些次要的难以建模的因素，例如空气阻力、伺服电机由于安装而产生的静摩擦力、系统连接处的松弛程度、摆杆连接处质量散布不均匀、传动皮带的弹性、传动齿轮的间隙等。

将小车抽象为质点，摆杆抽象为匀质刚体，摆杆绕转轴转动，如此就能够够通过力学原理成立较为精准的数学模型。

咱们能够应用牛顿力学的分析方式或欧拉－拉格朗日原理成立系统的动力学模型。

关于直线一级倒立摆如此比较简单的系统，咱们采纳通俗易懂的牛顿力学分析法建模。

为了成立直线一级倒立摆的数学模型，采纳如下的坐标系：图1直线一级倒立摆的物理模型其中，F 为加在小车上的力，M 为小车质量，m 为摆杆质量，I 为摆杆惯量， l 为摆杆转动轴心到杆质心的长度，x 为小车位移，φ为摆杆与垂直向上方向的夹角，b 为小车在滑轨上所受的摩擦力，N 和P 为摆杆彼此作使劲的水平和垂直方向的分量。

直线一级倒立摆控制器设计_课程设计说明书[管理资料]

H a r b i n I n s t i t u t e o f T e c h n o l o g y课程设计说明书（论文）课程名称：控制系统设计课程设计设计题目：直线一级倒立摆控制器设计院系：班级：设计者：学号：指导教师：设计时间：哈尔滨工业大学教务处哈尔滨工业大学课程设计任务书*注：此任务书由课程设计指导教师填写。

一、直线一级倒立摆的数学模型实验设备简介一级倒立摆系统的结构示意图如图1-1所示。

图1-1 一阶倒立摆结构示意图系统组成框图如图1-2所示。

图1-2 一级倒立摆系统组成框图系统是由计算机、运动控制卡、伺服机构、倒立摆本体和光电码盘几大部分组成的闭环系统。

光电码盘1将小车的位移、速度信号反馈给伺服驱动器和运动控制卡，摆杆的角度、角速度信号由光电码盘2反馈给运动控制卡。

计算机从运动控制卡中读取实时数据，确定控制决策（小车运动方向、移动速度、加速度等），并由运动控制卡来实现该控制决策，产生相应的控制量，使电机转动，通过皮带，带动小车运动，保持摆杆平衡。

直线一级倒立摆数学模型的推导系统建模可以分为两种：机理建模和实验建模。

实验建模就是通过在研究对象上加上一系列的研究者事先确定的输入信号，激励研究对象并通过传感器检测其可观测的输出，应用数学手段建立起系统的输入－输出关系。

这里面包括输入信号的设计选取，输出信号的精确检测，数学算法的研究等等内容。

机理建模就是在了解研究对象的运动规律基础上，通过物理、化学的知识和数学手段建立起系统内部的输入－状态关系。

对于倒立摆系统，由于其本身是自不稳定的系统，实验建模存在一定的困难。

但是经过小心的假设忽略掉一些次要的因素后，倒立摆系统就是一个典型的运动的刚体系统，可以在惯性坐标系内应用经典力学理论建立系统的动力学方程。

下面我们采用其中的牛顿－欧拉方法建立直线型一级倒立摆系统的数学模型。

在忽略了空气阻力，各种摩擦之后，可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统. 如图1-3所示。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

度为：Ｄ＝叫ｓ＋￣ＣＯＳ００ ≤ｓ ≤Ｌ．（３）
以导轨中点为原点建立固定坐标系ｘｏｙ，以摆杆
转轴中心为原点建立移动直角坐标系Ｘ０Ｙ，则倒立摆的状态完全由０点在ｘｏｙ系中的横坐标ｚ和摆杆角度０确定，这里是摆杆与竖直向下方向的夹角，且规定逆时针方向为正方向。倒立摆系统的受力分析如
高仿真直线一级倒立摆模型设计鬻
戴源成，张文志
（内蒙古工业大学机械学院了直线一级倒立摆的带有阻力效应的非线性数学模型，推导了直线一级倒立摆摆杆在摆动过程中所受到的介质阻力和摩擦力的计算公式，并利用ＭＡＴＬＡＢ的Ｓ函数建立了直线一级倒立摆的高仿真模型。
一一丁ｍｕｌｃｏｓＯ一
ＬＸ＝＝＝
＋＋
．
２倒立摆所受介质阻力的计算我们提出的介质阻力计算方法基于以下假设： ① 摆杆迎风面沿摆杆长度方向是均匀一致的； ② 介质阻力正比于速度的ａ次方，比例系数为ｐ。现在考虑摆杆角度为，摆杆角速度为ｆ．Ｏ，同时摆杆小车以速度口作水平运动时，摆杆所受的空气阻力，该阻力，可等效为作用于转轴的力，（，与，的值相等）和空气阻力对转轴的矩ＭＪ。如图２所示，设Ａ为摆杆转轴中心点，Ｂ为摆杆末端端点，在摆杆上任取一点Ｄ，设ＡＤ的长为ｓ（Ｏ ≤ｓ ≤ Ｌ），则Ｄ点处的迎风速
通过设置仿真模型的相关参数，可使仿真倒立摆与真实倒立摆的工作状态非常接近。关键词：倒立摆；仿真模型；介质阻力；摩擦力中图分类号：ＴＰ３９１．７文献标识码：Ａ
第５期（总第１８６期）
２０１４年１Ｏ月
机械工程与自动化ＭＥＣＨＡＮＩＣＡＬＥＮＧｌＮＥＥＲ１ＮＧ＆ＡＵＴ０ＭＡＴ１０Ｎ
Ｎｏ．５
０ｃｔ．
文章编号：１６７２ — ６４１３（２０１４）０５ — ０００１ — ０３
为ｍ。
速度对摆杆的影响表现为一作用于摆杆质心、方向与加速度相反的惯性力，其大小为ｍｕ。摆杆的摆动可视为刚体定轴转动，因此应满足如下微分方程Ｌ５］：
｛ＪＭ０，一＝一ｌＶＬ，
ｌ
，一一
ｏ
ｍｕｌｃｏｓＯ－ｍｇｌｓｉｎＯ＋Ｍ．ｒ２。
（１）
其中：Ｍ０，为作用于摆杆上各外力对转轴的矩；Ｍｆｚ为阻力，对转轴的矩，是介质阻力对转轴的矩ＭＪ和转轴摩擦力对转轴的矩Ｍ的和，Ｍｐ＝Ｍｊ＋Ｍｍ。因此摆杆摆角０和转轴位移ｚ应满足的方程为：
０引言
图１所示，根据非惯性系动力学的相关知识『４］，小车加
倒立摆是非线性、高阶次、多变量强耦合的自不稳定系统，是控制领域经常讨论的问题［１］。研究倒立摆一般先要建立倒立摆的数学模型，大多数研究人员建立的倒立摆模型都是理想化的、线性化的，未考虑空气阻力和转轴摩擦力的影响，在这样的模型上开发出来的控制方法应用到真实倒立摆上存在较大的偏差甚至不可行。本文提出了直线一级倒立摆的带有阻力效应的非线性数学模型，重点研究了直线一级倒立摆摆杆在摆动过程中所受到的介质阻力和摩擦力的计算方法，利用Ｓｉｍｕｌｉｎｋ的Ｓ函数建立了高仿真非线性虚拟倒立摆，通过调整Ｓ函数的相关参数，使虚拟倒立摆与真实倒立摆具有非常接近的工作状态，因而在虚拟倒立摆上获得的结论通常也适用于对应的真实倒立摆。１直线一级倒立摆的非线性数学模型直线一级倒立摆通常由摆杆、摆杆小车及电机伺服系统等组成，其电机伺服系统的输出可分为力矩输出和加速度输出两种形式。采用加速度输出形式时，系统以小车加速度 “为输入量，系统模型相对比较简单，因此我们以加速度为输入量来建立系统模型，并假设：摆杆是刚体；摆杆杆长为Ｌ；摆杆质心到转轴中心的距离为１；摆杆关于转轴的转动惯量为Ｊ；摆杆质量