工程力学 第十六章
工程力学-第十六章

16.5.2 纯弯曲正应力的分布规律
由平面假设可知,矩形截面梁在纯弯曲时的应力分布有如下特点: (1)中性轴上的线应变为零,所以其正应力亦为零。 (2)距中性轴距离相等的各点,其线应变相等。根据胡克定律,它们的正应力也相等。 (3)在图所示的受力情况下,中性轴上部的各点正应力为负值,中性轴下部的各点正应 力为正值。 (4)正应力沿y轴呈线性分布,如图所示,其中,K为待定常数。最大正应力(绝对值) 在距中性轴最远的上、下边缘处。
16.1.1 对称弯曲的概念
工程中最常见的梁,其轴线是直线,横截面一般都有1根或2根对称轴,如图所示。
16.1.1 对称弯曲的概念
由横截面的纵向对称轴和梁的轴线组成的平面,称为纵向对称面,如图所示。如果梁上的 外力全部作用在这个对称面内,那么梁变形后,其轴线也将变成这个对称面内的一条平面曲线, 这种弯曲称为平面弯曲。
04
弯矩、剪力与载荷集度间的关系
16.4 弯矩、剪力与载荷集度间的关系
一般情况下,梁上不同截面的 FQ 和 M 是不同的。为描述内力沿梁轴变化的规律,用 x 轴表示梁横 截面的位置,则梁各横截面上的剪力和弯矩可表示为坐标 x 的函数,即
FQ FQ (x) M M (x)
16.4 弯矩、剪力与载荷集度间的关系
Wz
πd 3 32
16.5.3 纯弯曲正应力的计算公式
常见截面的惯性矩和抗弯截面系数:
截面形状
惯性矩
抗弯截面系数
Iz
Iy
πD4 64
(1
α4)
Wz
πD3 32
(1
α4)
16.5.4 弯曲切应力简介
1.矩形截面梁横截面上的切应力
梁横截面上的切应力不是均匀分布的,对于矩形截面梁横截面上的切应力,假设其分布特 点为:
工程力学C16

2 确定零杆
零杆与桁架所承受的主动载荷有关。同一桁架在不 同的载荷下,零杆可能不同
若某节点与三杆相 连,节点上无主动 力,两杆平行,则 第三杆为零力杆 (右图 4 杆)
3 截面法
不宜截断三杆以上,适于校核部分杆件内力
已知:尺寸、载荷 求:杆4、5、6的内力
解:先由整体平衡求出A、B处的约束反力;再作截面I,
已知:尺寸、载荷 求:各杆内力
简单桁架,静定问题。 首先求约束反力, 考虑整体平衡:
∑m
A
= 0,
∑F
ix
= 0,
∑F
iy
=0
可求出:
N B , N Ax , N Ay ( N Ax = 0 )
用节点法求各杆内力,考虑各节点平衡的顺序:
A→ D→C → F → E →G → H
节点A (各杆内力均设为拉力)
=0 =0
F Ay + F22 sin 60 − FE = 0 F Ay + F sin 60 − FE = 0 FE × 0 ..5 m + F33 × FE × 0 5 m + F × 3 3 × 1 m − F Ay × 1 ..5 m = 0 × 1 m − F Ay × 1 5 m = 0 2 2
工程力学 C
北京理工大学理学院 尚玫
§3.4 桁架的内力计算
一、关于平面桁架的基本假设(理想桁架)
1. 各杆在端点用光滑铰链相连接,连接点称为节点 2. 杆的自重相对外载荷可以忽略不计 3. 载荷及支座反力均作用在节点上。 在以上假设下各杆均为二力杆,内力为拉力或压力
二、桁架的节点
1 桁架的实际节点:焊接或铆接,杆的端点不能 转动,可承受力矩 2 理想节点:光滑铰链,不能承受力矩
工程力学第16章(压杆稳定问题)

解:⑴ 计算压杆柔度
i d 11.25mm 4
两端为铰链约束
1
il11.1 2 5 0.1 70362.2
P
2E P
2200109
200106 100
62.2
压杆平衡稳定
压力小于一定的数值
时,压杆的直线平衡是 稳定的。
压杆平衡非稳定
当压力达到一定数值,压 杆仍具有直线平衡方式;在 外界扰动下,压杆偏离直线 平衡位置,但当扰动除去后, 在某一弯曲状态下达到新的 平衡
压力达到一定的数值时, 压杆存在直线和弯曲两种平 衡形式,压杆的直线平衡是 不稳定的。
压杆失稳
解: ⑴ 梁的强度校核(拉伸与弯曲的组合) 经过分析,AB 的危险截面为C 截面
F N F c o s 3 0 o 2 5 0 .8 6 6 2 1 .6 5 k N
M y F s i n 3 0 o l 1 2 5 0 .5 1 .2 5 1 5 .6 3 k N m 查型钢表
1 0 5 .5 2
4 7 3 k N
钢柱的许可载荷
F2 F nsctr
473157.7kN 3
例:图所示结构中,梁AB 为No.14 普通热轧工字钢,支承的杆 直径d = 20mm ,二者的材料均为Q235钢。结构受力如图所示,A 、B 、C 三处均为球铰约束。已知F = 25kN ,l1 = 1.25m ,l2 = 0.55m ,E = 206GPa 。规定稳定安全因数nst = 2.0 ,梁的许用应力 [σ] = 170MPa 。试校核此结构是否安全。
解:⑴ 压杆稳定校核(折减因素法)
工程力学判断选择

第一章静力学基础一、判断题1-1、如物体相对于地面保持静止或匀速运动状态,则物体处于平衡。
()1-2、作用在同一刚体上的两个力,使物体处于平衡的必要和充分条件是:这两个力大小相等、方向相反、沿同一条直线。
( ) 1-3、静力学公理中,二力平衡公理和加减平衡力系公理仅适用于刚体。
( ) 1-4、二力构件是指两端用铰链连接并且指受两个力作用的构件。
( ) 1-5、对刚体而言,力是滑移矢量,可沿其作用线移动。
()1-6、对非自由体的约束反力的方向总是与约束所能阻止的物体的运动趋势的方向相反。
()1-7、作用在同一刚体的五个力构成的力多边形自行封闭,则此刚体一定处于平衡状态。
()1-8、只要两个力偶的力偶矩相等,则此两力偶就是等效力偶。
()二、单项选择题1-1、刚体受三力作用而处于平衡状态,则此三力的作用线( )。
A、必汇交于一点B、必互相平行C、必都为零D、必位于同一平面内1-2、力的可传性()。
A、适用于同一刚体B、适用于刚体和变形体C、适用于刚体系统D、既适用于单个刚体,又适用于刚体系统1-3、如果力F R是F1、F2二力的合力,且F1、F2不同向,用矢量方程表示为F R= F1+ F2,则三力大小之间的关系为()。
A、必有F R= F1+ F2B、不可能有F R= F1+ F2C、必有F R>F1, F R>F2D、必有F R<F1, F R<F21-4、作用在刚体上的一个力偶,若使其在作用面内转移,其结果是()。
A、使刚体转动B、使刚体平移C、不改变对刚体的作用效果D、将改变力偶矩的大小第二章平面力系一、判断题2-1、平面任意力系向作用面内任一点简化,主矢与简化中心有关. ()2-2、平面任意力系向作用面内任一点简化,主矩与简化中心有关。
( ) 2-3、当平面一任意力系对某点的主矩为零时,该力系向任一点简化的结果必为一个合力。
( ) 2-4、当平面一任意力系对某点的主矢为零时,该力系向任一点简化的结果必为一个合力偶。
工程力学第16章课件
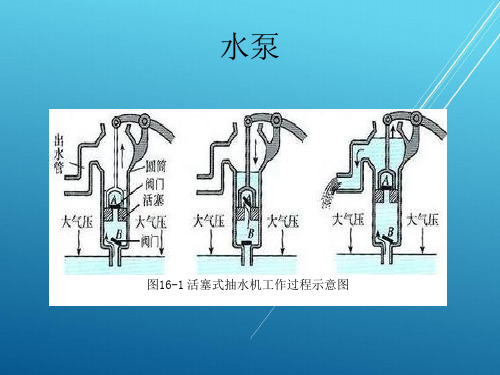
轴向柱塞泵特性
• 具有结构紧凑、单位功率体积小、重量轻、 容积效率高、工作压力高、易变量等优点;
• 缺点是结构复杂、造价高、对油的污染敏 感、使用和维修要求严格。
人力轴向活塞泵-汽车制动总泵
图16-14制动总泵组成示意图
制动总泵工作状态
(a)踩下踏板时
(b)松开踏板时
外啮合齿轮泵
• 优点:结构简单、工 作可靠、成本低、对 液压油的污染不太敏 感、便于维护等;
• 缺点:噪声高、油压 较低、流量脉动较大, 只能作定量泵使用。
汽车上外啮合齿轮泵应用
(a)
(b)
图16-8 外啮合齿轮泵实物图片
(内啮合)齿轮泵
(a)
(b) 图16-9内啮合齿轮泵结构原理图
内啮合齿轮泵
1 容积泵
液压泵工作条件
1.应具备密封工作容积,密封容积应不断重复地 由小变大,再由大变小;
2.要有配流装置,在吸油过程中必须使油箱与大 气相通,以保证密封容积减小时实现吸油。
•压油效率高于吸油。 •气阻是泵送液体时,系统内因存在可 压缩膨胀气体出现的供油不足或中断现 象。
排气效率高于进气
排气门
• 老王告诉小张,就这样开着盖子跑,车行驶一段时间还不会有 问题,但该考虑发动机大修了。尔后两人告别,各自驾车顺利 返回驻地。
• 整个救援过程,老王对小张的发动机只有一个几秒钟的动作, 卸下加机油口盖,就使发动机恢复运转。这其中的奥妙究竟在 哪儿呢?
想一想
想一想
• 一天晚上,将近11点,汽车修理厂厂长老王在家中 接到客户小张的求助电话,小张装有货物的“五十 铃”现在路上“抛锚”,不能动弹。问明现象后, 老王马上驾驶一辆备有汽修工具箱的“桑塔纳”赶 往抛锚地。临近半夜,“桑塔纳”很快与“五十铃” 见了面。老王下车,拿出工具,围绕发动机,展开 检查。打开起动开关,只见发动机在转却不能着车。 老王略加思索,伸手将发动机加机油口的罩盖取下, 再次起动,发动机在起动机带动几转后,轰然着车。
工程力学7-2-c16c

EA EI
l
D
EI
A
B
l
X1 a EA X 1 EI
C
D
l
2.正则方程 11 X 1 1t 1 0
26
例题
例 题 16-10
EI
A
§I6
静不定结构
3.求系数:
令 X 1 1 画内力图 M 1 FN 1
B
l
=1 X1 a =1 EA X 1 EI
C
D
l
(M 1 )
1 l
§I6
F
B
静不定结构
F
C
FN F
B
a
A
a
a
a
2次静不定
a
a
对称结构,对称载荷,对称 轴所在截面有中间铰
F
A
C
F a 1次静不定
B
切取一半结构,C截面处只有对 称内力——M,FN——C又为中 间铰,故该截面M=0
a
a
10
例题
例 题 16-8(2)
F
A C
§I6
F
B
静不定结构
F
C
F FS
B
a
A
a
a
1 1F 11
5.在相当系统上求 M A 利用平衡条件: q 1 1 3 2 M A qa a qa a qa (右侧受压) 2 8 8 a 1 q A (MF)
a
X1
A
MA
(b)
( M1 )
16
§16.5
装配应力和温度应力
静定结构:只在载荷作用下才产生内力和应力。 静不定结构:只要存在使结构变形的因素(除载荷外,装 配误差、温度、湿度变化等),都会产生内力和应力。 装配应力和温度应力求解思路: 静不定系统 相当系统 (X i为多余未知力)
工程力学第十六章

4、临界应力总图
cr
s
p
cr s
cr a b
cr
π2E
2
0
s
p
课堂讨论 如图所示3根压杆的材 料及截面都相同,那一种情 况的压杆最容易发生失稳? 说明理由(时间:1分钟)。
F F F
5m
A
7m
B
9m
C
F F F
A: B: C:
l 1 5 5
( n 0 ,1, 2 ,......)
上式表明,使杆件保持为曲线平衡 的压力,理论上是多值的。在这些压力 中,使杆件保持为曲线平衡的最小压力, 才是临界压力。
取n = 1
2 EI Fcr 2 l
两端铰支压杆的欧拉公式
(a)
F (b)
2、其它支承情况下细长压杆的临界力
不同约束形式 压杆的临界力,可 以用类似的方法求 解微分方程导出。 但在已经导出 两端铰支压杆的临 界压力公式之后, 便可以用比较简单 的方法,得到其他 约束条件下的临界 力。
1、计算柔度
活塞杆为圆形截面,故其惯性半径 属于中柔度杆
d i 4
l 0.7 3500 4 81.6 i 120
2、计算临界应力及临界压力
cr a b 460 2.568 81.6 250 .45MPa
π Fcr cr A 25.045 10 0.12 2 2831 .1kN 4
a s s b
(中长杆)。
304 235 s 61 .6 1 .12 工程中将柔度介于s 和p 之间的这一类压杆称为中柔度杆
3、小柔度杆 对于 < s的压杆,小柔度杆将因压缩引起 屈服或断裂破坏,属于强度问题,当然也可以将 屈服极限 s(塑性材料)和强度极限 b(脆性 材料)作为极限应力。
《工程力学》第十六章 压杆稳定
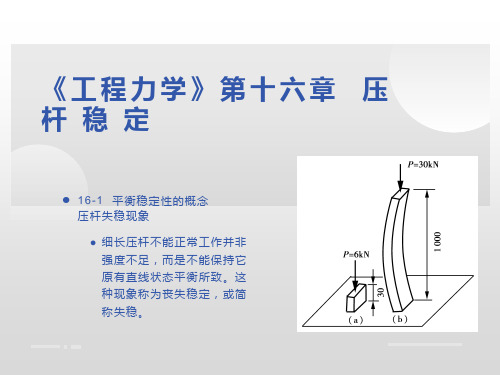
• 式中:I和A都是与截面有关的几何量,如果将 惯性矩写成横截面面积与某一距离平方的乘积, 即I=Ai2。i称为此横截面面积对于某一轴的惯性 半径。如果截面对y轴或z轴的惯性半径分别为
• 其量纲为长度一次方。常见图形的惯性半径 可从有关手册中查到。将I=Ai2代入(a)式得
•或
• 式中 P——工作压力; • Plj——压杆临界压力; • nw——压杆工作时实际具有的稳定安全
系数; • [nw]——规定的稳定安全系数。 • 也可采用应力形式表示压杆稳定性条件,
将式(16-10)及式(16-11),同除以压杆 的横截面面积A得
•或
• 式中[σw]——稳定许用应力。
• 二、折减系数法 • 由式(16-12)可知,压杆的稳定条件为
• 一、减小压杆的支承长度
• 由大柔度杆的临界应力公式
可
知在压杆材料一定的条件下,临界应力与
柔度的平方成反比,压杆的柔度愈小,相
应的临界应力愈高。而柔度
与压
杆长
• 度l成正比,减小压杆支承长度是降低柔度的方 法之一,在条件允许的情况下,应尽可能地减 小压杆的长度。例如,钢铁厂无缝钢管车间的 穿孔机的顶杆(图16-14),为了提高其稳定性, 在顶杆中段增加一个抱辊装置,这就达到了提 高顶杆稳定性的目的。
于是,压杆稳定性条件可以写成
• 对于已有压杆,其λ已知,可直接查表163得φ,代入式(16-14)进行稳定性校核。至
于设计截面尺寸,可采用逐次逼近法,即先
设定一个φ值,由式(16-14)计算出A值,然
后进行验算、调整,使杆件的工作应力逐渐 靠近许用应力。
表16-3.tif
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
σcr = a − bλ
a、b 是和材料有关的常数,单位是MPa 是和材料有关的常数,单位是MPa
σcr = a − bλ
经验公式也有一个适用的范围,即使用经验公式得到的临界 经验公式也有一个适用的范围, 应力不允许超过材料的极限应力,对于塑性材料, 应力不允许超过材料的极限应力,对于塑性材料,不能超过其屈 服极限,而对于脆性材料,不能超过其强度极限。 服极限,而对于脆性材料,不能超过其强度极限。当临界应力超 过极限应力后,压杆已经因为强度不足而破坏, 过极限应力后,压杆已经因为强度不足而破坏,这样经验公式计 算的结果是毫无意义的。 算的结果是毫无意义的。 对于塑性材料: 对于塑性材料: 令 σ cr = σ s 对于Q235钢 对于Q235钢:
引入记号
λ=
µl
i
π2E
则压杆的临界应力可表示为
σcr =
柔度(长细比) 柔度(长细比)
λ=
µl
i
λ2
式中λ 是一个没有量纲的量,称为柔度或长细比。它集中反应 是一个没有量纲的量,称为柔度或长细比。 了压杆的长度 l、约束条件µ 、截面尺寸和形状 i 等因素对临界 的影响。 应力σcr 的影响。
2、欧拉公式的适用范围 在欧拉公式的推导过程中,用到了挠曲线近似微分方程, 挠曲线近似微分方程, 在欧拉公式的推导过程中,用到了挠曲线近似微分方程 这就决定了材料必须符合胡克定律。 这就决定了材料必须符合胡克定律。 材料符合胡克定律 工作应力(临界应力) 工作应力(临界应力)小于比例极限σp
压杆丧失直线形式平衡状态的现象称为 丧失稳 失稳。 定,简称 失稳。 当压杆的材料、尺寸和约束情况已经确定时, 当压杆的材料、尺寸和约束情况已经确定时, 临界压力是一个确定的值。 临界压力是一个确定的值。因此可以根据杆件的实际 工作压力是否大于临界压力来判断压杆是稳定还是不 稳定。解决压杆稳定的关键问题是确定临界压力。 稳定。解决压杆稳定的关键问题是确定临界压力。
π2E
λ
取 λ = P
2
≤σP
λ≥
π2E
σP
π2 E
σP
则只有当 λ ≥ λP 欧拉公式才是有效的。 欧拉公式才是有效的。
通常将 λ ≥ λP 的杆称为大柔度杆(细长杆)。大柔度杆的临 的杆称为大柔度杆 细长杆) 大柔度杆( 界应力可以采用欧拉公式来进行计算。 界应力可以采用欧拉公式来进行计算。
3、中柔度杆的经验公式 对于λ < λp的压杆,其临界应力大于材料的比例极限,欧拉 的压杆,其临界应力大于材料的比例极限, 公式已经不适用。 公式已经不适用。 工程中这类问题一般采用经验公式。经验公式是根据试验 工程中这类问题一般采用经验公式。 数据整理后得到的, 数据整理后得到的,这里介绍工程中常用的直线公式 ,即
上式即为欧拉公式的一般形式。 上式即为欧拉公式的一般形式。
2
µl为相当长度, 相当长度, 长度因数, µ为长度因数, µ
与压杆两端的支 承情况有关。 承情况有关。其 数值为
两端铰支 一端固定一端自由 两端固定 一端固定一端铰支
µ=1 µ=2 µ = 0.5 µ = 0.7
两端铰支 µ=1.0
一端自由, 一端铰支, 一端自由, 一端铰支, 一端固定 一端固定 µ=2.0 µ=0.7
3、压杆失稳的特点 压杆失稳后,压力的微小增加将引起弯曲变形的显著增大, 压杆失稳后,压力的微小增加将引起弯曲变形的显著增大, 从而使杆件丧失承载能力。但是压杆失稳时, 从而使杆件丧失承载能力。但是压杆失稳时,杆内的应力不一定 有时甚至低于材料的比例极限。可见, 高,有时甚至低于材料的比例极限。可见,压杆失稳并非强度不 由于压杆稳定是突然发生的, 足。由于压杆稳定是突然发生的,因此所造成的后果也是很严重 的。
F = cr
π 2EI
l2
两端铰支压杆的欧拉公式
2、其它支承情况下细长压杆的临界力
不同约束形式 压杆的临界力, 压杆的临界力,可 以用类似的方法求 解微分方程导出。 解微分方程导出。 但在已经导出 两端铰支压杆的临 界压力公式之后, 界压力公式之后, 便可以用比较简单 的方法, 的方法,得到其他 约束条件下的临界 力。
1、稳定平衡和不稳定平衡
2、压杆失稳与临界压力 理想压杆: 材料绝对理想;轴线绝对直;压力绝对沿轴线作用。 理想压杆: 材料绝对理想;轴线绝对直;压力绝对沿轴线作用。
F小于某个值
F大于某个值
稳定平衡
不稳定平衡
临界状态 稳 定 过 平 衡
对应的
压力
临界压力: Fcr 临界压力:
不 稳 度 定 平 衡
π 2 EI π 2 × 200 × 103 × 108 × 104 Fcr = = N = 85187N = 85.19kN 2 2 ( µl ) (2 × 2500)
1、临界应力与柔度
16.3 欧拉公式的适用范围 及经验公式
将临界压力除以压杆的横截面面积A 将临界压力除以压杆的横截面面积A,就可以得到与临界压力 对应的应力为
一端铰支另一端固定的压杆的临界压力为: 一端铰支另一端固定的压杆的临界压力为: 两端铰支为: 两端铰支为:
π2EI Fcr = 2 l
π2EI F = cr (2l)2
一端铰支,一端自由: 一端铰支,一端自由:
综合各种不同的约束条件,统一写成如下形式: 综合各种不同的约束条件,统一写成如下形式:
π EI F = cr (µl)2
* 参考本章关于欧拉公式适用条件的相关内容
一端固定,一端自由,长度因数 一端固定,一端自由,
µ=2
在应用欧拉公式时,截面的惯性矩应取 在应用欧拉公式时, 较小的I 较小的I值。
hb 3 90 × 403 Iy = = mm 4 = 48 × 10 4 mm 4 12 12 bh 3 40 × 90 3 Iz = = mm 4 = 243 × 10 4 mm 4 12 12
a −σ s λs s = = 61.6 1.12 之间的这一类压杆称为中柔度杆 工程中将柔度介于λs 和λp 之间的这一类压杆称为中柔度杆
3、小柔度杆 对于λ < λs的压杆,小柔度杆将因压缩引起 的压杆, 屈服或断裂破坏,属于强度问题, 屈服或断裂破坏,属于强度问题,当然也可以将 塑性材料) 屈服极限 σs(塑性材料)和强度极限 σb(脆性 材料)作为极限应力。 材料)作为极限应力。
Iy < Iz
按照 Iy计算临界压力。 计算临界压力。
按照 Iy计算临界压力。 计算临界压力。
π 2 EI π 2 × 200 ×103 × 48 ×104 N Fcr = = 2 2 (2 × 2500) ( µl )
= 37860N = 37.86kN
若
h = b = 60mm
bh 3 60 4 Iy = Iz = = mm = 108 × 10 4 mm 12 12
一端固定,一端自由, 一端固定,一端自由, 长为l 长为l 的的压杆的挠曲线 和两端铰支,长为2 和两端铰支,长为2l的 压杆的挠曲线的上半部 分相同。则临界压力: 分相同。则临界压力:
π2EI F = cr (2l)2
同样: 同样: 两端固定的压杆的临界压力为: 两端固定的压杆的临界压力为:
π 2 EI Fcr = (0.5l ) 2 π 2 EI Fcr = (0.7l ) 2
16.2 临界力的计算
1、两端铰支杆 图示坐标系, 图示坐标系,考察微弯状态下任意 一段压杆的平衡( ),杆件横截面上 一段压杆的平衡(图b),杆件横截面上 的弯矩为: 的弯矩为:
M ( x) = F ⋅ w( x)
根据挠曲线近似微分方程,有 根据挠曲线近似微分方程,
取
d 2 w( x) M ( x) = − EI dx 2 F 2 k = EI d 2 w( x) + k 2 w( x) = 0 dx 2
F k2 = EI
d 2 w( x) + k 2 w( x) = 0 dx 2
解微分方程得到通解为
w( x) = C1 sin kx + C 2 cos kx
C1和C2为待定常数,根据压杆的约束边 为待定常数, 界条件来确定,在两端铰支的情况下, 界条件来确定,在两端铰支的情况下, 边界条件为
w(0) = w(l ) = 0
C2 = 0,
C1 ⋅ sin kl = 0
w( x) = C1 sin kx + C 2 cos kx C2 = 0, C1 ⋅ sin kl = 0
若C1=0,表明杆为直线,这与压杆处于 =0,表明杆为直线, 微弯平衡状态不符。 微弯平衡状态不符。
sin kl = 0
kl = nπ (n = 0,1,2,....)
4、压杆失稳造成的灾难 1907年 1907年8月9日,在加拿大离魁北克城14.4Km横跨圣劳伦斯河的 在加拿大离魁北克城14.4Km横跨圣劳伦斯河的 大铁桥在施工中倒塌.灾变发生在当日收工前15分钟 桥上74人坠河 分钟, 大铁桥在施工中倒塌.灾变发生在当日收工前15分钟,桥上74人坠河 遇难.原因是在施工中悬臂桁架西侧的下弦杆有二节失稳所致. 失稳所致 遇难.原因是在施工中悬臂桁架西侧的下弦杆有二节失稳所致. 杭州某研发生产中心的厂房屋顶为园弧形大面积结构, 杭州某研发生产中心的厂房屋顶为园弧形大面积结构,屋面采 用预应力密肋网架结构,密肋大梁横截面(600mm×1400mm),屋面 用预应力密肋网架结构,密肋大梁横截面(600mm×1400mm),屋面 采用现浇板,板厚120mm .2003年 18日晚 时 当施工到26~28轴 日晚19 采用现浇板,板厚120mm .2003年2月18日晚19时,当施工到26~28轴 支模架失稳坍塌,造成重大伤亡事故。 失稳坍塌 时,支模架失稳坍塌,造成重大伤亡事故。 美国哈特福特城的体育馆网架结构,平面92m×110m,突然于 美国哈特福特城的体育馆网架结构,平面92m×110m,突然于 1978年破坏而落地 破坏起因可能是压杆屈曲 以及1988年加拿 1978年破坏而落地,破坏起因可能是压杆屈曲。以及1988年加拿 年破坏而落地, 压杆屈曲。 大一停车场的屋盖结构塌落,1985年土耳其某体育场看台屋盖塌 大一停车场的屋盖结构塌落,1985年土耳其某体育场看台屋盖塌 这两次事故都和没有设置适当的支撑有关。 没有设置适当的支撑有关 落,这两次事故都和没有设置适当的支撑有关。
