双曲抛物面
叶双曲面与双曲抛物面

2021/4/22
12
2021/4/22
13
定理 单叶双曲面
x2 a2
y2 b2
z2 c2
1 , a,b, c
0
是直纹曲面。它有两族直母线:
w
x a
z c
u
1
y b
,
w2 u2
0
u
x a
z c
w 1
y b
,
(4.7-1)
与
t
x a
z c
v
1
y b
,
t2 v2
0
,
v
x 3
z 4
t
1
y 2
.
将(6,2,8)代入上述直母线族方程,求得 w , u , t , v.
2021/4/22
17
例题
例2
试证明双曲抛物面
x2 a2
y2 b2
上2z 的a 两b直母线直交时,其交点必
在一双曲线上.
例3 已知空间两异面直线间的距离为 2,a夹角为 ,2过这两直线
分别作平面,并使这两平面相互垂直,求这样的两平面交线的轨
迹.
2021/4/22
18
y b
(4.7-1)
与
t
x a
z c
v
1
y b
,
t2 v2
0
v
x a
z c
t
1
y b
.
(4.7-2)
推论1 对于单叶双曲面上的点,两族直母线中各有一条直母线通
过这点.
8
Back
皮肌炎图片——皮肌炎的症状表现
• 皮肌炎是一种引起皮肤、肌肉、 心、肺、肾等多脏器严重损害的, 全身性疾病,而且不少患者同时 伴有恶性肿瘤。它的1症状表现如 下:
双曲抛物面

几个探究性问题:
1.证明双曲抛物面的直纹性。
2.探究双曲抛物面在生活中的更多应用。
3.为什么一个顶点粘7个等边三角形,会形成双曲抛
物面?这和曲面的曲率有什?
一扇打开的窗,可以看到更多美丽的风景!
谢谢大家!
休闲座椅
双曲抛物面与水利工程
梯形的渠道与矩形闸孔连接
参考资料 :
1.《解析几何》 吕林根、许子道 高等教育出版社,高等教育出版社; 第4版 (2006年5月1日) 2.How to Make a Hyperbolic Paraboloid Using
Skewers,/howto/make-hyperbolic-paraboloid-using-skewers0131751. 3.Paraboloid Pictures: /o/ pictures/topic/12383450/Paraboloid. 4.Pleating Paraboloids,/current/ events/pleating-paraboloids/.
双曲抛物面
双曲抛物面
双曲抛物面的方程及其图像 双曲抛物面的直纹性 双曲抛物面的应用
1.方程及其图像
x y 0 2 2 z 2 a b
2 2
z
O
y
x
2.双曲抛物面的直纹性
问题:双曲抛物面能否由直线构成?
双曲抛物面可以由直线构成,并且有两族直母线。
3.双曲抛物面的应用
夏威夷休闲度假厅
单叶和双叶双曲面方程

单叶和双叶双曲面方程单叶和双叶双曲面是数学中的重要概念,它们在几何和物理学中都有广泛的应用。
本文将介绍单叶和双叶双曲面的定义、方程以及它们的性质和应用。
1. 单叶双曲面1.1 定义单叶双曲面是三维空间中的一个曲面,其形状类似于一个向上凸起的碗或者双曲抛物面。
单叶双曲面在数学中也被称为双曲抛物面。
1.2 方程单叶双曲面的方程可以表示为:x^2/a^2 + y^2/b^2 - z^2/c^2 = 1其中,a、b和c分别是该双曲面在不同方向上的半轴长度。
1.3 性质和应用单叶双曲面具有多种特性和应用,以下是其中一些重要的性质和应用:•对称性:单叶双曲面具有关于z轴和原点的对称性。
对于所有的z值,曲面在对称轴上都有一个顶点。
•双曲线截面:单叶双曲面在任意平行于xy平面的截面上都生成双曲线。
•焦点和准线:单叶双曲面有两个焦点和两条准线,焦点对曲面的形状和性质具有重要影响。
单叶双曲面在物理学、工程学和计算机图形学中有广泛的应用,例如:•天体力学:单叶双曲面被用来描述天体之间的引力场。
•天线设计:单叶双曲面天线可以实现大范围覆盖,提高信号接收和发射的效果。
•三维建模:单叶双曲面可以用于建模和渲染三维物体。
2. 双叶双曲面2.1 定义双叶双曲面也是三维空间中的一个曲面,与单叶双曲面相比,它的形状更类似于一个马鞍或者双曲抛物面。
双叶双曲面在数学中也被称为双曲双曲面。
2.2 方程双叶双曲面的方程可以表示为:x^2/a^2 - y^2/b^2 - z^2/c^2 = 1其中,a、b和c分别是该双曲面在不同方向上的半轴长度。
2.3 性质和应用双叶双曲面具有一些与单叶双曲面相似的性质和应用,但也有一些重要的差异,以下是其中一些性质和应用:•对称性:双叶双曲面也具有关于z轴和原点的对称性。
对于所有的z值,曲面在对称轴上都有一个鞍点。
•双曲线截面:双叶双曲面在任意平行于xz平面或yz平面的截面上都生成双曲线。
•焦点和准线:双叶双曲面有两个焦点和两条准线,与单叶双曲面的特性类似。
单叶双曲面与双曲抛物面
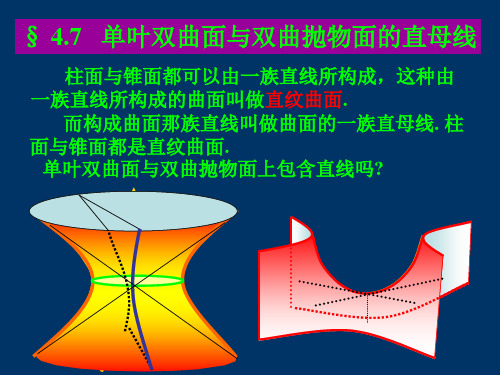
对于给定的u,
(3)表示什么曲线? (3)与(2)等价吗?
x z y a c u 1 b x z 1 1 y a c u b
直线
(3) 不等价!
x2 y2 z2 2 2 1, 2 a b c
(1) (2)
这是因为
z x 0, a c y 0; 1 b
z x 0, a c y 0. 1 b
u族直线满足于
x z x z y y 1 1 . a c a c b b
(4.7Hale Waihona Puke 4)分别称为u族和v族直母线.
双曲抛物面是直纹面
x2 y 2 2 2z 2 a b
含两族直母线
也有下面的推论:
推论 对于双曲面与抛物面上的点,两族直母 线中各有一条直母线通过这一点. 单叶双曲面与双曲抛物面的直母线,在建筑上 有着重要的应用,常常用它来构成建筑的骨架。 单叶双曲面与双曲抛物面的直母线还有下面 的一些性质: 定理4.7.1 单叶双曲面上异族的任意两直母线必共 面而双曲抛物面上异族的任意两直母线 必相交.
(3)
考虑到(3) 与(2)相比,漏掉了下面的两个方程组
z x a c 0, (4) 1 y 0; z x b a c 0, 与 y 0. 1 b
(4)/
也就是说
x z y u 1 a c b x z 1 1 y a c u b
满足于
x y z 2 2 1, 2 a b c
2
2
2
(1)
反过来,设 ( x0 , y0 , z0 )是曲面(1)上的点.
试析在实际生活中双曲抛物面的作用

试析在实际生活中双曲抛物面的作用摘要:在几何中,由一族直线运动所产生的曲面叫做直纹面,这些运动的直线称为直母线。
双曲抛物面就是典型的直纹面,并且它有两族直母线。
本文通过对双曲抛物面的直纹性进行研究,探索了双曲抛物面在建筑、电力工程、日常生活、宇宙学中的应用,并进一步研究了手工制作双曲抛物面的方法。
关键词:几何双曲抛物面手工制作直纹性在生活中,比如随意舞动一根棍子,棍子运动的轨迹面就会包含直线,这样的曲面就是由直线构成,而双曲抛物面正是这样一种曲面。
它是由两族直线分别组成,正是因为这种特殊性使得这种曲面有一些特性,在生活中有它独特的应用。
定义1:[1]在几何中,由一族直线运动所产生的曲面叫做直纹面,这些运动的直线称为直母线。
定义2:[2]在直角坐标系下,由方程表示的曲面叫做双曲抛物面,其中a,b为任意的正常数。
双曲抛物面的直纹性:[3]性质1:双曲抛物面是直纹面,是直线运动所产生的曲面。
性质2:同一族的任意两条直母线异面。
性质3:任意一条直母线会和另一族所有的直母线相交。
性质4:对双曲抛物面上的任意一点,两族直母线中各有一条直母线经过该点。
一、双曲抛物面在实际生活中的应用双曲抛物面可以由直线运动所产生,易于在建筑中实施,且其形状不同于一般的平面型建筑,它集美观与实用于一体。
因此,双曲抛物面在工程等方面有着广泛的应用。
(一)扭面。
水利工程中的扭面是利用双曲抛物面形状构造的,它是水闸、船闸的中间连接面。
水闸侧墙是直立剖面,扭面ABCD部分是采用的双曲抛物面,这种扭面构造可以使水流平顺,减少水头损失,在工程中应用广泛。
(二)屋盖。
现代建筑中经常采用钢筋混泥土双曲抛物面薄壳作为屋盖,例如夏威夷休闲度假厅、波兰华沙火车站等。
不仅外观新颖有创意性,在实用性方面具有利于排水、防止渗漏、减轻自重节约材料、受力性能较好等优点。
双曲抛物面是直纹面,任意一条直母线会和另一族所有的直母线相交。
这样,在一条直母线上,被另一族直母线分摊受力,相互作用,相互稳固。
§4.6 抛物面

§4.6 抛物面一、椭圆抛物面1.在直角坐标系下,由方程+=2z所表示的曲面叫做椭圆抛物面, 该方程叫做椭圆抛物面的标准方程, 其中a, b为任意正常数.2. 椭圆抛物面的图形(如图4-7).(1) 曲面的对称性:椭圆抛物面关于yOz, zOx坐标面以及z轴对称, 但它没有对称中心, 它与对称轴交于点(0, 0, 0), 这点叫做椭圆抛物面的顶点.(2) 曲面与坐标轴的交点:椭圆抛物面通过坐标原点, 且除原点外, 曲面与三坐标轴没有别的交点.(3) 曲面的存在范围:椭圆抛物面全部在xOy坐标面的一侧, 即在z≥0的一侧.(4) 被坐标面截得的曲线①②③①表示一点(0, 0, 0), 而②与③分别为xOz与yOz坐标面上的抛物线, 它们有着相同的顶点和相同的对称轴即z轴, 开口都向着z轴的正向,都叫做椭圆抛物面的主抛物线.(5) 被坐标平面的平行平面所截得的曲线:用平行于xOy坐标面的平行平面z=h(h>0)来截椭圆抛物面, 得截线方程为+=1. ④椭圆抛物面可看成是由椭圆族④所生成, 这族椭圆中的每一个椭圆所在的平面与xOy坐标面平行, 两顶点分别在双曲线②与③上.用平行于xOz坐标面的平面y=k来截割椭圆抛物面,所截得的曲线为抛物线用平行于yOz坐标面的平面来截椭圆抛物面所得的截线也是抛物线.若a=b, 则椭圆抛物面就是旋转抛物面.3. 椭圆抛物面的参数方程为(u, v是参数)二、双曲抛物面1. 在直角坐标系下, 由方程-=2z所表示的曲面叫做双曲抛物面, 如图5-8, 该方程叫做双曲抛物面的标准方程, 其中a, b为任意正常数.2. 双曲抛物面的图形(如图4-8).(1) 曲面的对称性:双曲抛物面关于xOz坐标面, yOz坐标面以及z轴都对称, 但它没有对称中心.(2) 曲面与坐标轴的交点:双曲抛物面通过原点, 且除原点外与三坐标轴没有其它交点.(3) 被坐标面所截得的曲线:双曲抛物面被xOy坐标面截得的曲线方程为⑤这是一对相交于原点的直线与被xOz与yOz坐标面截得的曲线方程分别为⑥⑦这两抛物线叫做双曲抛物面的主抛物线, 它们有着相同的顶点与相同的对称轴, 即z轴, 但开口方向相反.(4) 被坐标面的平行平面所截得的曲线:用平行于xOy坐标面的平面z=h来截割双曲抛物面, 得截线方程为⑧这是双曲线, 当h>0时, 双曲线⑧的实轴与x轴平行, 虚轴与y轴平行, 顶点(±a, 0, h)在主抛物线⑥上; 当h<0时,双曲线⑧的实轴与y轴平行, 虚轴与x轴平行, 顶点(0, ±b,h)在主抛物线⑦上.用分别平行于xOz与yOz坐标面的平面y=k与x=t来截曲面,其截线都是抛物线, 方程分别为⑨⑩抛物线⑨的对称轴平行于z轴, 且开口方向与z轴正向相同, 顶点(0, k, -)在主抛物线⑦上; 抛物线⑩的对称轴也平行于z轴, 但开口方向与z轴的正向相反, 顶点(t, 0,)在主抛物线⑥上.双曲抛物面也叫做马鞍曲面.椭圆抛物面与双曲抛物面统称为抛物面, 它们都没有对称中心,所以又都叫做无心二次曲面.3. 双曲抛物面的参数方程为(u, v为参数)例1. 在空间直角坐标系中, 求与直线l1:==和l2:==共面且与平面 :x-y-5=0平行的直线所组成的轨迹.解:设满足条件的直线方程为==,由直线与l1共面得=0,或 (4y0+z0-4)X+(-4x0+z0+4)Y+(-x0-y0+z)Z=0. ①由直线与l2共面得=0,或z0X+z0Y+(―x0―y0)Z=0. ②由直线平行于平面π得X-Y=0. ③因为X, Y, Z不全为零, 所以由上面①、②、③构成的齐次线性方程组应有非零解, 因而=0,化简得x02-y02=z0.其中 (x0, y0, z0) 表示所求直线上的点, 从而满足条件的直线所组成的轨迹是双曲抛物面x2-y2=z.例2. 适当选取坐标系, 求下列轨迹的方程:(1) 到一定点和一定平面距离之比等于常数的点的轨迹;(2) 与两给定异面直线等距离的点的轨迹,已知两异面直线之间的距离为2a, 夹角为2α.解:(1) 设定点到定平面的距离为h>0, 常数c>0. 取定平面为xOy平面, z轴垂直于定平面并通过定点建立直角坐标系, 设定点坐标为(0, 0, h), 动点坐标为(x, y, z), 依题意有,化简整理得x2+y2+(1-c2)z2-2hz+h2=0.讨论:当h=0时, 方程为x2+y2+(1-c2)z2=0,(i) c>1时为圆锥面;(ii) c=1时为z轴;(iii) c<1时为一点(0, 0, 0).当h≠0时,(i) c>1时为旋转双叶双曲面;(ii) c=1时为旋转抛物面;(iii) c<1时为旋转椭球面.(2) 取两异面直线的公垂线为z轴, 公垂线中点为原点, 并取轴与两异面直线成等角建立空间直角坐标系, 设公垂线与两异面直线的交点分别为E (0, 0, a), F (0, 0, -a).则两异面直线的方向矢量分别为={cosα, sinα, 0}, ={cosα, -sinα,0}.设动点为P(x, y, z), 依题意有=,即 |{cosα, sinα, 0}×{x, y, z-a}|=|{ cosα, -sinα, 0}×{x, y, z+a}|,化简整理得2az+xy sin2α=0.该曲面表示一个双曲抛物面.例3.画出下列各组曲面所围成的立体的图形:(1) y=0, z=0, 3x+y=6, 3x+2y=12, x+y+z=6;(2) x2+y2=z, 三坐标面, x+y=1;(3) x=, =x, y=1;(4) x2+y2=1, y2+z2=1.解:如下图作业题:1. 判断下列方程表示什么曲面, 并画出草图.(1) 4y2+z2=4x;(2) 3x2-5y2+15z=0 .2. 方程+=z (a>b>0, k为参数)表示一族无心二次曲,问k取何值时,二次曲面为椭圆抛物面、双曲抛物面?。
单叶双曲面与双曲抛物面

(4.7-1) 4.7-
与
(4.7-2) 4.7-
推论1 推论1
对于单叶双曲面上的点, 对于单叶双曲面上的点,两族直母线中各有一条直母线 Back
通过这点. 通过这点.
三、双曲抛物面是直纹曲面
z
O
y
x
三、双曲抛物面是直纹曲面
双曲抛物面
x2 y2 2 = 2z 2 a b (a, b > 0 )
总是异面直线,而且双曲抛物面同族的全体直母线平行于同一 总是异面直线,而且双曲抛物面同族的全体直母线平行于同一 同族
例题
例1 求过单叶双曲面
x2 y 2 z 2 + = 1 上的点 ( 6, 2,8 ) 的直母线的方程. 的直母线的方程. 9 4 16
x2 y2 z 2 两族直母线方程为 方程为: 分析: 分析: 单叶双曲面 + = 1 的两族直母线方程为: 9 4 16
例(教材P153) 教材P153)
x 求直线 Γ: = y = z 1 绕直线 l : x = y = z 旋转所 2 1 0 得的旋转曲面的方程. 得的旋转曲面的方程.
单叶旋转双曲面
Back
直纹曲面模型
直纹曲面模型
二、单叶双曲面是直纹曲面
单叶双曲面
x2 y2 z2 + 2 2 =1 2 a b c ( a, b, c > 0)
x y a + b = 2u, (u ∈ R ) u x y = z , a b x y a b = 2v, (v ∈ R) . x y v + = z , a b
(4.7-3) 4.7-
与
(4.7-4) 4.7-
对于双曲抛物面上的点,两族直母线中各有一条直母线通过该 对于双曲抛物面上的点,两族直母线中各有一条直母线通过该点.
双曲面
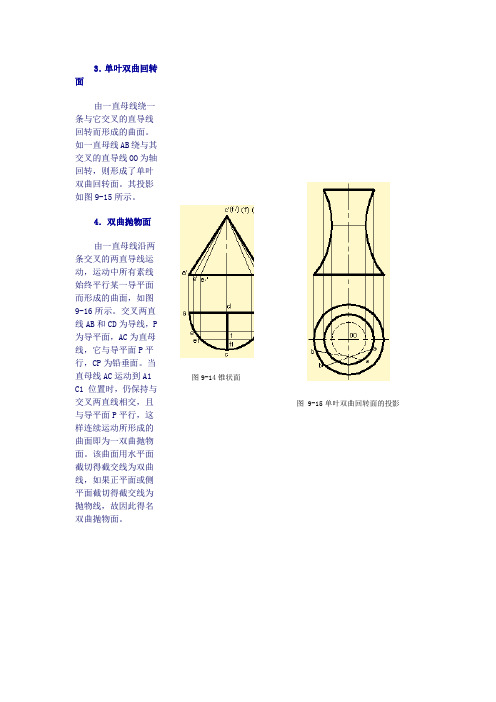
3.单叶双曲回转面由一直母线绕一条与它交叉的直导线回转而形成的曲面。
如一直母线AB绕与其交叉的直导线OO为轴回转,则形成了单叶双曲回转面。
其投影如图9-15所示。
4.双曲抛物面由一直母线沿两条交叉的两直导线运动,运动中所有素线始终平行某一导平面而形成的曲面,如图9-16所示。
交叉两直线AB和CD为导线,P 为导平面,AC为直母线,它与导平面P平行,CP为铅垂面。
当直母线AC运动到A1 C1 位置时,仍保持与交叉两直线相交,且与导平面P平行,这样连续运动所形成的曲面即为一双曲抛物面。
该曲面用水平面截切得截交线为双曲线,如果正平面或侧平面截切得截交线为抛物线,故因此得名双曲抛物面。
图9-14锥状面图 9-15单叶双曲回转面的投影曲纹面以任意的平面曲线为母线绕回转轴旋转而形成的曲面称为曲纹面。
常见曲纹面有回转椭球面、回转抛物面等。
1.回转椭球面回转椭球面是椭圆绕其自身的长轴或短轴旋转而形成的曲面。
图 9-17所示的回转椭球面的投影,是绕长轴旋转形成的,正面投影是椭圆本身大小,而水平投影是以短轴为直径的圆。
2.回转抛物面回转抛物面是抛物线绕其对称轴旋转而形成的曲面。
回转抛物面的正面投影就是抛物线本身,而水平投影是圆,如图 9-18所示。
图 9-16 双曲抛物面图 9-17回转椭圆面 图9-18回转抛物面4.7单叶双曲面与双叶双曲面的直母线1、 求下列直纹面的直母线族方程: (1)(2)解:(1)从原方程得:x y z +-=axy z =222y z x -=-即:亦即:为了避免取极限,将上方程写成:(1)若将原方程变形为:,则可得到:(2)若令,,则(2)便是(1)原曲面的直母线族是(1),其中不全为零。
(2)原方程变形为:亦即:(1)y y z x z x ⋅-=-+))((⎩⎨⎧-=-=+⇔=--=+y t z x ty z x t z x yy z x )(⎩⎨⎧-=-=+sy t z x tyz x s )()(222x z y -=-⎩⎨⎧-=-=+ux z y v vxz y u )()()(21s t u -=)(21s t v +=∴t s ,ay x z=tay x z==⎩⎨⎧==∴t ay xt z由得: (2)(1)(2)即这原曲面的两组直母线族方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z
0
x
z y
0
x-y=0 x
yz
0
y
x
四 二次曲面 称三元二次方程F(x, y, z) 0所表示的曲面为二次曲面。 Ax2 By2 Cz2 Dx Ey Fz G 0(A, B,C不全为零) 而Ax By Cz 0表示的的曲面称为一次曲面---平面。
问题:给定方程F(x,y,z)=0,如何确定方程所 表示的曲面形状?
三、柱面 例7 在空间直角坐标系中,方程x2 y2 R2表示怎样的曲面?
解:在xoy面上,x2 y2 R2表示圆。 显然直线L上点M (x, y, z)满足
x2 y2 R2 故曲面:x2 y2 R2称为圆柱面 圆x2 y2 R2 ---准线, L 母线(平行于z轴) 定义 平行于定直线,并沿定曲线C移 动的直线L形成的轨迹叫做柱面 定曲线C 准线, 动直线L 母线
, x2 y2
f ( y1, z ) 0
得f ( x2 y2 , z) 0 为所求旋转曲面方程。
同理: 曲线C : f ( y, z) 0绕y轴旋转的曲面方程为 f ( y, x2 z2 ) 0
曲线C : f (x, z) 0绕x轴旋转的曲面方程为 f (x, y2 z2 ) 0
3
3
即 (x 2)2 (y 1)2 (z 4)2 ( 2 39)2
3
33
---球心( 2 , 1, 4),半径R 2的球面
3
3
3
求面方程的一般形式 Ax2 Ay2 Az2 Dx Ey Fz G 0(A 0)
特点 缺xy, yz, zx;平方项系数相等 例3 设有点A(1, 2,3)和B(2, 1, 4),求线段AB的垂直平分面的方程。
一般的
F(x, y) 0 母线 z轴的柱面 G(x, z) 0 母线 y轴的柱面 特点:缺一个变量
H ( y, z) 0 母线 x轴的柱面
例8
x2 a2
y2 b2
1 母线
z轴的双曲柱面;
x y 0 过z轴的平面;
z2 5 母线 轴的柱面。
: z x2 y2 cot 0
即z2 cot2 (x2 y2 ) 圆锥面方程
-- 圆锥的半顶角 若= ,则
4 :z2 x2 y2
例6 建立xoz面上抛物线z2 5x分别绕x轴,z轴旋转一周所 形成曲面的方程,并画图。 解:绕x轴旋转的曲面方程:z2 5 x2 y2 绕z轴旋转的曲面方程:y2 z2 5x
z
o x
o
yx
y
特别的:
x2 y2 z2
a=b时,方程
a2
2
b
c2
1为旋转椭球面
a=b=c时,方程为 x2 y2 z2 a2 为球面
绕z轴旋转的曲面方程为 f ( x2 y2 , z) 0
曲线C : f (x, y) 0绕x轴旋转的曲面方程为 f (x, y2 z2 ) 0
绕y轴旋转的曲面方程为 f ( x2 z2 , y) 0
例5 yoz平面上直线L : z cot y绕z旋转的曲面方程:
例2 求与原点O及点A(2,3, 4)的距离之比为1: 2的点的轨迹方程, 并判断其性状。
解:设M (x, y, z)为曲面上任一点,则
| OM | 1 | AM | 2
x2 y2 z2 1 (x 2)2 (y - 3)2 (z 4)2
2
所求方程为 x2 y2 z2 4 x 2 y 8 z 29 0
解决方法:采用截痕法,即用坐标面及平行于 坐标面的平面去截曲面,观察所的截线的形状, 从而确定曲面图形。
下面讨论几个特殊的二次曲面
一、椭球面
方程
:x 2
a2
y2 b2
z2 c2
1,
(a 0,b 0, c 0)
首先: x a,
y b, z c
其 次 : 与 xoy 坐 标 面 的 交 线 ( 截 痕 )
解:设M (x, y, z)为平面上任一点,则 | AM || BM |
即 (x 1)2 (y - 2)2 (z 3)2 (x 2)2 (y 1)2 (z 4)2
整理化简 2x 6y 2z 7 0 平面方程,三元一次方程
例4
问:空间坐标系中,方程(1) z
c0
x2
:
a
2
y2 b2
z2 c2
1
x2
a
2
y2 b2
1
z 0
z 0
是xoy面上的椭圆
பைடு நூலகம்
再看:与 z z0( z0 c) 平面的交线
x2
y2
z z cz0
x2
:
a
2
y2 b2
z z0
z2 c2
1
a
2
1
z z0
2 0
c2
b 2 1
2 0
c2
1
是 z z0 平面上的椭圆
最后与平面 z c 相交于点 (0,0,c)
综上讨论,可知椭球面 形状如图
Z
X Y
类似的,若用平行于xoz及yoz坐标面的两组平面 截椭球面,得到的解痕仍是两组椭圆,如图
z
曲线C-母线 定直线L-轴
M (x, y, z)
0
z
0
C : f (x, y) 0 M1(x, y, z)
y
x
设C为yoz平面上一条曲线,
C : f (y, z) 0
建立曲线C绕z轴旋转的曲面 的方程
解:设M (x, y, z)为上任一点,则M点是由C上一点旋转所成,故
z1 z y1
0, (2)z
4,
(3)
x y
0 0
各表示什么图形?
解:(1)z 0 xoy坐标面
(2)z 4 平行于xoy面且距离为4的平面
x 0
(3) z
y
0
yoz与zox面的交线,即z轴
z
o
x
4
o
y
y
x
定义 一条平面曲线绕着平面上一条直线旋转一周所成的曲面 叫做旋转曲面。
