单叶双曲面与双曲抛物面
单叶双曲面和双曲抛物面的直母线

z 4
v 1
y 2
,
v
x 3
z 4
t
1
y 2
.
将(6,2,8)代入上述直母线族方程,求得 w , u , t , v.
例题
例2
试证明双曲抛物面
x2 a2
y2 b2
2z a
b上的两直母线直交时,其
交点必在一双曲线上.
z c
v
1
y b
,
t2 v2
0
v
x a
z c
t
1
y b
.
(4.7-2)
推论1 对于单叶双曲面上的点,两族直母线中各有一条直母线通
过这点.
B8ack
三、双曲抛物面是直纹曲面
z
O x
y
9
三、双曲抛物面是直纹曲面
双曲抛物面
例3 已知空间两异面直线间的距离为 2a,夹角为 2 ,过这两
直线分别作平面,并使这两平面相互垂直,求这样的两平面交线
的轨迹.
2020/1/21
18
x2 a2
y2 b2
2z
a,b 0
悉尼歌剧院
定理 单叶双曲面
x2 a2
y2 b2
z2 c2
1 , a,b, c
0
是直纹曲面。它有两族直母线:
w
x a
z c
u
1
单叶双曲面与双曲抛物面

z c
w 1
y b
,
(4.7-1)
与
t
x a
z c
v
1
y b
,
t2 v2
0
v
x a
z c
t
1
y b
,
(4.7-2)
对于单叶双曲面上的点,两族直母线中各有一条直母线通过这点.
定理 双曲抛物面
x2 a2
y2 b2
2z ,
是直纹曲面.它有两族直母线:
a,b 0
x
y b
z,
u
R
(4.7-3)
与
x a
y b
2v,
v
x a
y b
z,
v
R
.
(4.7-4)
对于双曲抛物面上的点,两族直母线中各有一条直母线通过该点.
四、单叶双曲面与双曲抛物面的性质
定理4.7.1 单叶双曲面上异族的任意两直母线必共面,而双曲抛 物面上异族的任意两直母线必相交. 定理4.7.2 单叶双曲面或双曲抛物面上同族的任意两直母线总 是异面直线,而且双曲抛物面同族的全体直母线平行于同一平 面.
通过这点.
Back
三、双曲抛物面是直纹曲面
z
O
y
x
三、双曲抛物面是直纹曲面
双曲抛物面
x2 a2
y2 b2
2z
a,b 0
悉尼歌剧院
定理 单叶双曲面
x2 a2
y2 b2
z2 c2
1 , a,b, c
0
是直纹曲面。它有两族直母线:
w
x a
z c
u
1
y b
,
w2 u2
单叶双曲面与双曲抛物面的教法

单叶双曲面与双曲抛物面的教法
椭球-椭圆
双曲面-抛物面
(1) 双曲面:
1)定义:双曲面是单叶双曲面的特殊情况,由特定的二次多项式表示,它在三维空间中是一个曲面,它有二维和一维空间投影,它可以被椭
圆曲线拟合。
双曲面的特点是其曲率固定,且四条边界是正交的。
2)参数方程:双曲面的参数方程为
$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$,其中$a,b,c$都
大于零。
3)特征:双曲面有两个极轴:$x$和$z$轴;它有两个椭圆曲线为投影:椭圆$\frac{x^2}{a^2}+\frac{z^2}{c^2}=1$和
$\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$
(2) 双曲抛物面:
1)定义:双曲抛物面是由特定的一次多项式表示的抛物面,在三维空
间构成一个双曲面,它与椭球有着类似的几何结构,双曲抛物面的特
点是它的抛物度恒定,边界曲线与xy平面的交点为椭圆。
2)参数方程:双曲抛物面的参数方程为$\frac{x^2}{a^2}-
\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$,其中$a,b,c$都大于零。
3)特征:双曲抛物面有两个极轴:$x$和$z$轴;它有两个椭圆曲线为投影:椭圆$\frac{x^2}{a^2}+\frac{z^2}{c^2}=1$和$\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$。
河海大学理学院《高等数学》常用二次曲面图形

2020/4/4
67
图36:以下函数的图形:
z sin x cos y cosx y
0 x ,0 y
2
2
z sin x cos y cosx y 0 x ,0 y
2
2
2020/4/4
68
图37:锥面 z x2 y2 被柱面 z 2 2x
割下部分的曲面图形如下:
处的切平面及法线的图形如下:
P1,1,1
2020/4/4
40
图9:
(9)、 x t sin t, y 1 cos t, z 4 sin t , 2
在 1,1,2 2 处的切线和法平面如下 :
2
x t sin t, y 1 cost, z 4sin t , 2
在 1,1,2 2 处的切线和法平面如下 :
34
图6:
2020/4/4
35
图7:
(7)、x 0, y 0, z 0, y 1, z 4 2x2 y 2 ;
所围 图形如下:
2020/4/4
36
图7:
2020/4/4
37
图7:
2020/4/4
38
图7:
2020/4/4
39
图8:
(8)、椭球面 2x2 3y2 z2 6 在点 P 1,1,1
其中: p, q 为正常数。
2020/4/4
9
椭圆抛物面的图形
2020/4/4
10
双曲抛物面(马鞍面) 方程
方程: 其中:
x2 y2 2z
pq p, q 为正常数。
2020/4/4
11
双曲抛物面(马鞍面) 图形
2020/4/4
12
单叶双曲面与双曲抛物面
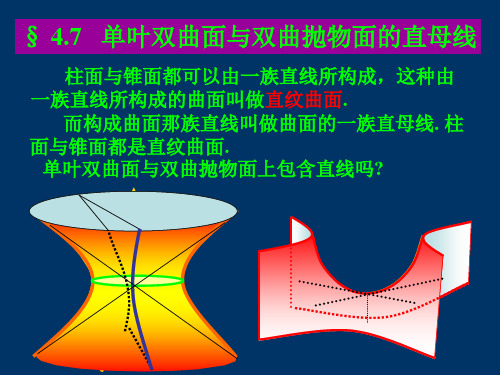
对于给定的u,
(3)表示什么曲线? (3)与(2)等价吗?
x z y a c u 1 b x z 1 1 y a c u b
直线
(3) 不等价!
x2 y2 z2 2 2 1, 2 a b c
(1) (2)
这是因为
z x 0, a c y 0; 1 b
z x 0, a c y 0. 1 b
u族直线满足于
x z x z y y 1 1 . a c a c b b
(4.7Hale Waihona Puke 4)分别称为u族和v族直母线.
双曲抛物面是直纹面
x2 y 2 2 2z 2 a b
含两族直母线
也有下面的推论:
推论 对于双曲面与抛物面上的点,两族直母 线中各有一条直母线通过这一点. 单叶双曲面与双曲抛物面的直母线,在建筑上 有着重要的应用,常常用它来构成建筑的骨架。 单叶双曲面与双曲抛物面的直母线还有下面 的一些性质: 定理4.7.1 单叶双曲面上异族的任意两直母线必共 面而双曲抛物面上异族的任意两直母线 必相交.
(3)
考虑到(3) 与(2)相比,漏掉了下面的两个方程组
z x a c 0, (4) 1 y 0; z x b a c 0, 与 y 0. 1 b
(4)/
也就是说
x z y u 1 a c b x z 1 1 y a c u b
满足于
x y z 2 2 1, 2 a b c
2
2
2
(1)
反过来,设 ( x0 , y0 , z0 )是曲面(1)上的点.
空间解析几何-第3章-常见的曲面2

把方程的左边都化成两项正,一项负,则右边是1的就 表示单叶双曲面,而右边是-1的,就表示双叶双曲面.
2°绘图时要注意区分“实轴”和“虚轴”,并且保证对坐 标轴的标注要符合右手系的原则.
1、椭圆抛物面
x2 a2
, 椭圆
z h.
O
结论:单叶双曲面可看作由一
个椭圆的变动(大小位置都改
x
y
变)而产生,该椭圆在变动中,
保持所在平面与xOy 面平行,
且两对顶点分别在两定双曲线
上滑动.
用平行于坐标面的平面截割
z
(2)用y = h 截曲面
x2 Cyh: a2
z2 c2
1
h2 b2
,
y h.
①当 h b时
截线为双曲线
o
y
用平行于坐标面的平面截割
(2)用y = h 截曲面
x2 Cyh: a2
z2 c2
0,
y h.
③当 h =b 时
截线为直线
(0 , b , 0)
单叶双曲面: x2 y2 z2 1 a2 b2 c2
用y = h 截曲面
①当 h b 时
②当 h b 时
③当 h =b 时
x2 Cyh: a2
x2 Czh: a2
y2 b2
h2 c2
1,
z h.
结论:双叶双曲面可看作由 一个椭圆的变动(大小位置 都改变)而产生,该椭圆在 变动中,保持所在平面与 x
xOy 面平行,且两轴的端点
分别在两定双曲线上滑动.
z
o
y
(2)用 y t截曲面
二次曲面的直纹性

二次曲面的直纹性一 定义:由一组连续变化的直线形成的曲面称为直纹面,其中每条直线都称为它的母线。
注:柱面、锥面显然都是直纹面,但椭球面,双叶双曲面与椭圆抛物面均不是直纹面。
试问,单叶双曲面与双曲抛物面是否为直纹面?答案是肯定的。
二 单叶双曲面的直纹性: 设有单叶双曲面 1222222=−+cz b y a x (1) (1)等价于 (c z a x +)(c z a x −)=⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛+b y b y 11 (2) 即 ⎟⎠⎞⎜⎝⎛+c z a x :⎟⎠⎞⎜⎝⎛+b y 1=⎟⎠⎞⎜⎝⎛−b y 1:⎟⎠⎞⎜⎝⎛−c z a x (3) 对∀ λ≠0,方程组 ⎪⎪⎩⎪⎪⎨⎧−=−+=+)1(1)()1()(b y cz a x b y c z a x λλ (4) 表示一直线,另外 ⎪⎪⎩⎪⎪⎨⎧=−=+010by c z a x (5) 及 ⎪⎪⎩⎪⎪⎨⎧=+=−010by c z a x (6) 也表示直线。
显然由(4)—(6)构成的直线族中每一直线均在单叶双曲面(1)上。
再者对∀0M (0x ,0y ,0z )∈(1) 有 ⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛+=⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛+b y 1b y 1c z a x c z ax 000000 注意1+b y 0与1-by 0不全为0 1°若1+b y 0≠0当时0c z a x 00≠+,令λ=0by 1c z a x 000≠++ 则 0M ∈(4) 当0c z a x 00=+时,则1-by 0 =0,则0M ∈(5) 2°若1+b y 0=0,则1-by 0≠0 当0c z a x 00≠− 取λ=cz a x b y 1000−−≠0 则0M ∈(4) 当0cz a x 00=−时,有0M ∈(6) ∴有:单叶双曲面是由直线族(4)-(6)构成的 ∴单叶双曲面是直纹面。
同理,由 ⎪⎪⎩⎪⎪⎨⎧+=−−=+1(1)1(b y c z a x b y c z a x µµ μ≠0 (4′) ⎪⎪⎩⎪⎪⎨⎧=+=+010by c z a x (5′) 及⎪⎪⎩⎪⎪⎨⎧=−=−010by c z a x (6′) 组成的直线族也可构成单叶双曲面(1),为方便记忆,将(4)—(6)和(4′)-(6′)写成如下统一形式 ⎪⎪⎩⎪⎪⎨⎧−=−′+′=+)1()(1()(b y u cz a x u b y u c z a x u u,u′不全为0 (7)⎪⎪⎩⎪⎪⎨⎧+=−′−′=+)1()()1()(b y v cz a x v b y v c z a x v v,v′不全为0 (7′)分别称(7)(7′)为单叶双曲面(1)的u 族,v 族直母线。
4.7 直纹面

( x0 , y0 , z0 ) 满足方程(2)
的某一直线上 ∴单叶双曲面(1) 由直线族 (2) 构成
M ( x0 , y0 , z0 ) 在直线族(2)
x z x z 1 y 1 y a c a c b b x z a c
λ不同, 所表示的直线也不同. 当λ取遍一切实数时, 得到无数多条直线, 这些直线构成一直纹面. 求此直纹面
的方程.
2z x 2 y z 解 消去λ y 3 1 2 3 2 2z 2z z y x y 3 3 3 z 2 4 2 4 y z yz x 0 为所求直纹面方程. 3 9 3
1 a a 1 a k a 1 b b 1 b k b
L1 :
0 2 1 0
1 a a 1 b b
1 1 x y 2 b a x y z 0 a b
证明: 对于双曲抛物面, 属于同族的两条直母线 都是 异面的. x y 2 2 a b 2 y 证x 2 2 z x y x y 2 z λ族: 2 a b a b a b x y z 在其中任取两条 a b 1 1 1 1 x y 2k x y 2 b L1 : b a L2 : a k k k x y z 0 x y z 0
R
(5.9)
x y a b 2
R
(5.10)
x y z a b
例 求双曲抛物面 4x y z 过点 M (1, 1, 3) 的直母线方程.
2 2
解
2x y 2x y z 2x y 2x y z
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
这两条直线共面的充分必要条件是(看p137, 例3)
四个方程的系数和常数项所组成的行列式为零.
w a u a t a v a u b w b v b t b w c u c t c v c u w w u w v t w u t v u w v t 1 u abc t v v t
另外,还有下面的定理.
定理 4.7.2 单叶双曲面或双曲抛物面上同族的任 意两直母线总是异面直线,而且双曲抛物面同族的全 体直母线平行于同一平面.
x y z 例 求过单叶双曲面 1上的点 4 16 (6,2,8)的直母线方程。 9 x2 y2 z 2 1的两族直线 解 单叶双曲面 9 4 16 方程是
含两族直母线
也有下面的推论:
推论 对于双曲面与抛物面上的点,两族直母 线中各有一条直母线通过这一点. 单叶双曲面与双曲抛物面的直母线,在建筑上 有着重要的应用,常常用它来构成建筑的骨架。 单叶双曲面与双曲抛物面的直母线还有下面 的一些性质: 定理4.7.1 单叶双曲面上异族的任意两直母线必共 面而双曲抛物面上异族的任意两直母线 必相交.
所以点 ( x0 , y0 , z0 ) 也在u直线上. 这样就证明了曲面(1)是由u族直线所构成. 因此单叶双曲面(1)是直纹曲面. 而u族直线是单叶双曲面(1)的一族直母线, 称为u族直母线
同样可以证明由直线 y x z a c v(1 b ), (6) x z 1 (1 y ) a c v b (其中 为不等于零的任意实数)与另两直线(相当与 (6)中当v 0和v 的情形)
即
x0 z0 x0 z0 y0 y0 1 1 . (5) b b a c a c
x0 z0 x0 z0 y0 y0 1 1 . (5) b b a c a c
方程组(4),(4`)实际上是(3)式中当参数 u 0 和 u 时的两种极限情形.
x z y u 1 a c b x z 1 1 y a c u b
(3)
z x 0, a c y 0; 1 b
由(5)便得
x0 z0 1 y0 1 , a c u b
所以点 在u直线上.
x0 z0 x0 z0 y0 y0 1 1 . (5) b b a c a c 如果 x0 z0 0 那么由(5)知必有 1 y0 0 a c b
4 x 12 y 3z 24 0, 4 x 3 y 3z 6 0;
与
y 2 0, 4 x 3z 0.
练习: p180. 1. 3. 作业: p180. 2. 6.
含两族直母线
.
直纹面在建筑学上有意义
例如,储水塔、 电视塔等建筑都 有用这种结构的.
推论 对于单叶双曲面上的点,两族直母线 中各有一条直母线通过这点. 为了避免取极限,我们常把单叶双曲面(1)的u 族直母线写成
y x z w( a c ) u (1 b ), u ( x z ) w(1 y ), a c b
x z x z 0, a c 0, a c (7)/ 与 (7) 1 y 0 y 1 0, b b 合在一起组成的直线族是单叶双曲面(1)的另一族直 母线.称它为单叶双曲面(1)的v族直母线.
单叶双曲面是直纹面
x2 y2 z2 1 1 . b b a c a c
x z y 1 a c b . (2)/ y x z 1 b a c
x z y u 1 a c b x z 1 1 y a c u b
满足于
x y z 2 2 1, 2 a b c
2
2
2
(1)
反过来,设 ( x0 , y0 , z0 )是曲面(1)上的点.
下面说明这个点一定在u族直线中的某一条上.
只须证明由这个点的坐标可以确定出参数u.
( x0 , y0 , z0 )是曲面(1)上的点. 所以满足单叶双曲面方程
x0 2 y0 2 z0 2 2 2 1, 2 a b c
显然
y0 与 y0 不能同时为零. ????? 1 1 b b y0 因此不失一般性, 假设 1 0 b x0 z0 0 那么取 u 的值使得 如果 a c x z
x0 z0 y0 u 1 , a c b
y u 1 a c b x z 1 1 y a c u b
§ 4.7 单叶双曲面与双曲抛物面的直母线
柱面与锥面都可以由一族直线所构成,这种由 一族直线所构成的曲面叫做直纹曲面. 而构成曲面那族直线叫做曲面的一族直母线. 柱 面与锥面都是直纹曲面. 单叶双曲面与双曲抛物面上包含直线吗?
下面我们来证明: 这两曲面不仅含有直线,而且可以由一族直线所构成.
因而它们都是直纹曲面.
(4.7-1)
其中 u, w不同时为零。当 u 0, w 0时,各式除以 w, (4.7 1) 式子就化为(3);当 u 0时便化成(4); 当 w 0 时便化成(4`).
x z y a c u 1 b x z 1 1 y a c u b
(3)
与
(4)与(4)/仍 然表示直线
z x 0, a c y 0; 1 b
(4)
z x 0, a c y 0. 1 b
(4)/
合起来与单叶双曲面(1)的方程等价. 把(3),(4),(4`)合起来组成的一族直线叫做单叶双曲面的 u族直线.
这是因为
z x 0, a c y 0; 1 b
z x 0, a c y 0. 1 b
u族直线满足于
x z x z y y 1 1 . a c a c b b
我们虽然很弯 曲, 但是我们都 由直线构成, 你相信吗?
首先考虑单叶双曲面
x y z 2 2 1, 2 a b c
其中 a, b, c 为正常数, 把(1)改写为
2 2 2
2
2
2
(1)
或者
x z y 2 1 2 , 2 a c b
(2)
x z x z y y 1 1 . a c a c b b
(4)
我们是 u族直线 家族成员
z x a c 0, y 0. 1 b
(4)/
现在来证明由这 u 族直线可以构成曲面(1),从 而它是单叶双曲面(1)的一族直母线。 首先容易知道, u族直线中任何一条直线上的点
都在曲面(1)上.
x z y a c u 1 b x z 1 1 y a c u b
(3)
而v族直母线写成
y x z t ( a c ) v(1 b ), v( x z ) t (1 y ), a c b
(4.7-2)
其中 v, t 不同时为零. 对于双曲抛物面
x y 2 2 z, 2 a b
同样地可以证明它也有两族直母线
2
(2)与(1)等价吗? 等价!
x z x z y y 1 1 . a c a c b b
改写为:
x z y 1 a c b . y x z 1 b a c
(2)
(2)/
现在引进不等于零的参数u, 将上述方程写为:
现在我们来证明定理的前半部分,单叶双曲面上 异族的任意两直母线必共面. 证: 单叶双曲面的两个异族直母线方程分别为:
x z y a c u 1 b x z 1 1 y a c u b
z y x v (1 ), a c b x z 1 (1 y ) a c v b
对于给定的u,
(3)表示什么曲线? (3)与(2)等价吗?
x z y a c u 1 b x z 1 1 y a c u b
直线
(3) 不等价!
x2 y2 z2 2 2 1, 2 a b c
(1) (2)
2
它们的方程分别是
x y a b 2u, u ( x y ) z , a b
与
(4.7-3)
x y a b 2v , v( x y ) z. a b
(4.7-4)
分别称为u族和v族直母线.
双曲抛物面是直纹面
x2 y 2 2 2z 2 a b
(3)
考虑到(3) 与(2)相比,漏掉了下面的两个方程组
z x a c 0, (4) 1 y 0; z x b a c 0, 与 y 0. 1 b
(4)/
也就是说
x z y u 1 a c b x z 1 1 y a c u b
y x z w( 3 4 ) u (1 2 ), 与 u ( x z ) w(1 y ); 3 4 2 y x z t ( ) v(1 ), 3 4 2 v( x z ) t (1 y ). 3 4 2
2
2
2
把点(6,2,8)分别代入上面两组方程,求得
w : u 1: 2
与
t 0,
