如何用圆规画椭圆(精.选)
椭圆的几种画法

课题2:椭圆的几种画法(本课题适合于高一数学必修课)机型:92-Plus教学过程:例1.已知椭圆的长a,短半轴的长为b。
1.显示直角坐标系,以原点为圆心作二个同心圆,半径分别为a、b。
(见图1)2.过原点作一条射线(F2、6 Ray),此射线交二个圆于M、N(F2、3 Intersection Point)(见图2)(图1)(图2)3.按F4、1 Perpendicular Line,分别过M点作垂直于y轴的直线,过N点作垂直于x轴的直线。
4.两直线的交点为P(F2、3 Intersection Point),隐藏不需要的线。
5.按F7、2 (Trace On/Off),将光标指向P点,按Enter,再将光标指向射线,按住,并配合移动光标方向键,即会出现点P的轨迹——椭圆(长轴在x轴上)。
(见图3)6.在上述过程中,如果过M点作垂直于x轴的直线,过N点作垂直于y轴的直线,则两线的交点P的轨迹(长轴在y轴上)。
(见图4)(图3)(图4)例2.根据椭圆的定义,条件是两个定点,及一条线段AB(线段AB的长大于两个定点间距离)。
方法一:1.在一个新的窗口中,作画两个点F1、F2及一条线段AB。
2.以线段AB的长为半径,以一个定点F1为圆心作一个圆(F4、8 Compass)。
(见图5)3.在作好的圆上取一点P(F2、2),连接PF1(F2、5)(见图6)(图5)(图6)4.作PF2的垂直平分线(F4、4 Perpendicular Bisector),交PF1于M(F2、3),再连接MF2(F2、5),这样使MF2、MF1的和等于定长AB。
(见图7)5.可以按F7、1隐藏不需要的线。
6.按F4、A(Locus),先选择点M,再选择点P,7.等待一会儿,即会出现椭圆的曲线。
(见图8)(图7)(图8)方法二、1.在一个新的窗口中,作画两个点F1、F2(F2、1)并在线段AB上任取一点P。
(见图9)2.以线段PA的长为半径,以F2为圆心,作一个圆,再以PB的长为半径,以F1为圆心,作另一个圆(F4、8 Compass),并按F2、3作出两圆的交点M、M'。
小学圆规练习题

小学圆规练习题题目一:利用圆规画等腰三角形1. 准备:一张白纸、一支铅笔、一把圆规、一支直尺。
2. 步骤:a. 用直尺画一条水平线,作为基准线。
b. 在基准线上选择一个点A,用铅笔做一个点标记。
c. 以点A为圆心,设置圆规的长度,用铅笔在基准线上作两个弧线,与基准线交于点B和点C。
d. 移动圆规的一只脚,以点B为圆心,再次画一个弧线与之前的交点处相交于点D。
e. 以点C为圆心,再次画一个弧线与之前的交点处相交于点E。
f. 将点D和点E连线,即得到一个等腰三角形ABC。
题目二:利用圆规画圆1. 准备:一张白纸、一支铅笔、一把圆规。
2. 步骤:a. 在白纸上选择一个中心点O,并用铅笔做一个点标记。
b. 调整圆规的长度,将一只脚放在点O,并用另一只脚在纸上画圆弧。
c. 围绕点O保持圆规的长度不变,移动圆规的一只脚,画出一条与之前圆弧交于一点的弧线。
d. 再次移动圆规的一只脚,画出另一条与之前两个交点相交的弧线。
e. 重复步骤d,直到画出一个封闭的曲线,即为所求的圆。
题目三:利用圆规画正方形1. 准备:一张白纸、一支铅笔、一把圆规、一支直尺。
2. 步骤:a. 用直尺画一条水平线,作为正方形的底边。
b. 在底边上选择一个点A,用铅笔做一个点标记。
c. 以点A为圆心,设置圆规的长度,用铅笔在直尺上作两个弧线,与直尺交于点B和点C。
d. 移动圆规的一只脚,以点B为圆心,再次画一个弧线与之前的交点处相交于点D。
e. 以点C为圆心,再次画一个弧线与之前的交点处相交于点E。
f. 将点D和点E连线,即得到一个正方形ABCD。
题目四:利用圆规画五边形1. 准备:一张白纸、一支铅笔、一把圆规、一支直尺。
2. 步骤:a. 在白纸上选择一个中心点O,并用铅笔做一个点标记。
b. 设置圆规长度,以点O为圆心,在纸上画一个圆弧。
c. 以刚刚画出的圆弧上的一点作为圆心,再次画一个圆弧。
d. 重复步骤c,共画出五个圆弧,相互交于五个点,形成一个封闭的曲线,即为所求的五边形。
椭圆画法

你用鸡蛋比着画应该可以吧。
有同心圆法,四心点法和相似菱形法,同心圆法比较简单。就是按照长短轴画两个圆,无数条直线通过圆心,其实就是若干条,然后大圆交点作垂线和小圆交电作平行线相交,就像个比较宽的直角三角形,交点直角的顶点就是椭圆上的点,然后用曲线板顺次连接,要是画多点就可以找到准确的用圆规画的半径 。
椭圆画法
一、四心近似法
已知相互垂直且平分的椭圆长轴和短轴,则椭圆的近似画法(四心近似法)步骤如下所示:
第一步:
画出长轴AB和短轴CD,连接AC;
第二步:
在AC上截取CF,使其等于AO与CO之差CE;
第三步:
作AF的垂直平分线,使其分别交AO和OD(或其延长线)于O1和O2点。以O为对称中心,找出O1的对称点O3及O2的对称点O4,此O1、O2、O3、O4各点即为所求的四圆心。通过O2和O1、O2和O3、O4和O3各点,分别作连线;
很简单。
现在桌面固定好两个点。在把一根细绳的两端系在两个点上,用铅笔把绳等紧,移动铅笔,其走过的痕迹就是一个椭圆。
高中课讲过用一根毛线,长度要求线的两端在十字的水平两端,将线的中间用笔撑直正好在十字的上端点。将两端固定,之后用笔撑着线画就好了。
一、四心近似法
已知相互垂直且平分的椭圆长轴和短轴,则椭圆的近似画法(四心近似法)步骤如下所示:
第四步:(双击恢复)
分别以O2和O4为圆心,O2C(或O4D)为半径画两弧。再分别以O1和O3为圆心,O1A(或O3B)为半径画两弧,使所画四弧的接点分别位于O2O1、O2O3、O4O1和O4O3的延长线上,即得所求的椭圆。
有同心圆法,四心点法和相似菱形法,同心圆法比较简单。就是按照长短轴画两个圆,无数条直线通过圆心,其实就是若干条,然后大圆交点作垂线和小圆交电作平行线相交,就像个比较宽的直角三角形,交点直角的顶点就是椭圆上的点,然后用曲线板顺次连接,要是画多点就可以找到准确的用圆规画的半径 。
木工画定尺椭圆法

木工椭圆画法(采用绳子画椭圆的方法)
装修中其实很多的造型都有椭圆,但又有很多人不知道在已知的尺寸下怎么画。
我来用最简单的方法解释下。
在你要画的板子(2400MM*1200MM)上分别取中线,长的我们叫X轴,短的叫Y轴,交点为O点。
比如我们要画长为2000MM,短为800MM的椭圆,那它的一半就是1000MM*400MM。
以O点为起点在Y轴上取400MM长A点,再以A点为起点取需要画的椭圆长轴的一半1000MM画圆与X轴有两个交点(O点左右两边各一点),分别为B、C,在这两点上分别钉一颗钉子,再以O点延X轴左右各取1000MM为D、E,取一没有弹性的绳子,长为以B点经过A点到C点,(AB的长度+AC的长度)把线固定在B、C两个钉子上,用笔绷紧绳划线经过A、E、F、D
详见下面示意图。
【参考借鉴】尺规作图五点定椭圆的方法.docx
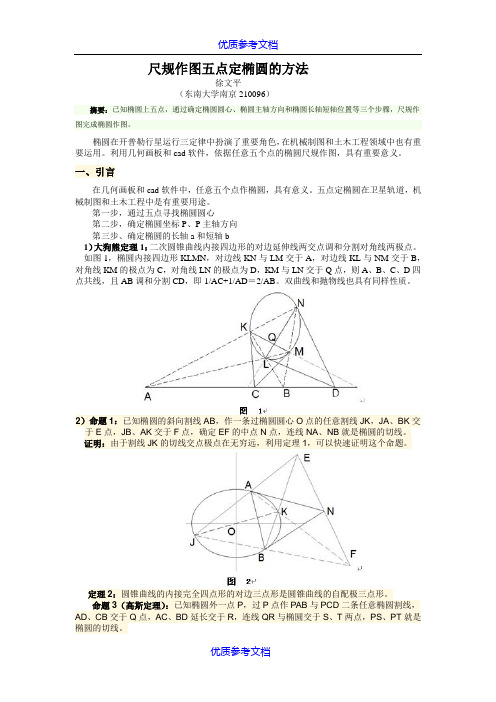
尺规作图五点定椭圆的方法徐文平(东南大学南京210096)摘要:已知椭圆上五点,通过确定椭圆圆心、椭圆主轴方向和椭圆长轴短轴位置等三个步骤,尺规作图完成椭圆作图。
椭圆在开普勒行星运行三定律中扮演了重要角色,在机械制图和土木工程领域中也有重要运用。
利用几何画板和cad软件,依据任意五个点的椭圆尺规作图,具有重要意义。
一、引言在几何画板和cad软件中,任意五个点作椭圆,具有意义。
五点定椭圆在卫星轨道,机械制图和土木工程中是有重要用途。
第一步,通过五点寻找椭圆圆心第二步,确定椭圆坐标P、P主轴方向第三步、确定椭圆的长轴a和短轴b1)大狗熊定理1:二次圆锥曲线内接四边形的对边延伸线两交点调和分割对角线两极点。
如图1,椭圆内接四边形KLMN,对边线KN与LM交于A,对边线KL与NM交于B,对角线KM的极点为C,对角线LN的极点为D,KM与LN交于Q点,则A、B、C、D四点共线,且AB调和分割CD,即1/AC+1/AD=2/AB。
双曲线和抛物线也具有同样性质。
2)命题1:已知椭圆的斜向割线AB,作一条过椭圆圆心O点的任意割线JK,JA、BK交于E点,JB、AK交于F点,确定EF的中点N点,连线NA、NB就是椭圆的切线。
证明:由于割线JK的切线交点极点在无穷远,利用定理1,可以快速证明这个命题。
定理2:圆锥曲线的内接完全四点形的对边三点形是圆锥曲线的自配极三点形。
命题3(高斯定理):已知椭圆外一点P,过P点作PAB与PCD二条任意椭圆割线,AD、CB交于Q点,AC、BD延长交于R,连线QR与椭圆交于S、T两点,PS、PT就是椭圆的切线。
图3二、通过五点寻找椭圆圆心原理:通过已知五点,作椭圆切线,获得割线的极点,将割线的极点和割线中点连接并延伸,必定通过椭圆的圆心。
图4问题1:只有五点,没有坐标轴和原点,椭圆斜的,割线PQ的切线极点如何办?切线方法:帕斯卡定理(五点+一个切点二次)做切线,或者如图5方法作切线。
几何画板探求椭圆轨迹的几种作法

几何画板探求椭圆轨迹的几种作法几何图形的绘制,我们通常是用直尺和圆规,它们的配合几乎可以画出所有的欧氏几何图形。
从某种意义上讲几何画板绘图是欧氏几何“尺规作图”的一种现代延伸。
因为这种把所有绘图建立在基本元素点、线、圆上的做法和数学作图思维中公理化思想是一脉相承的。
用几何画板探求椭圆的轨迹,可进一步理解椭圆的定义以及以动画形式展示动点轨迹如何形成椭圆。
让学生在数学的实验过程中体验数学之美及培养学生的创新能力。
几何画板绘图中,构造轨迹的前提条件是:选定两点,一点是在一条路径上的自由点和能够跟随此点运动的点即被动点。
其中路径可以是任何线(线段、直线、射线)轨迹、函数图象。
一、椭圆的定义椭圆的定义:到两个定点f1,f2的距离和等于常数2a(2a>f1f2)的点的轨迹叫做椭圆。
这两个定点f1,f2叫做椭圆的焦点。
根据椭圆的定义,在几何画板绘图中,我们要确保动点到两个定点的距离为常数且大于两定点间距离。
以下探求椭圆轨迹的实验环境为几何画板5.0环境下进行实验操作。
方法一:(1)在画板上作线段f1f2。
(2)在画板上作另一条线段ab,使ab>f1f2。
(3)在线段ab上任取一点c,“构造”线段ac;“构造”线段bc。
(4)以点f1为圆心、线段ac为半径,“构造”圆f1。
(5)以点f2为圆心、线段bc半径,“构造”圆f2。
(6)圆f1与圆f2交于点m、p,并选择“跟踪”点m、p。
(7)选中点c,在编辑菜单下操作类按钮设置为动画,标记为“动点m、p形成轨迹”。
(8)当鼠标点击“动点m、p形成轨迹”按钮时,点m、p运动,运点的轨迹是椭圆。
方法二:(1)在画板上作圆a,在圆内和圆上分别取点b、c,“构造”直线ac,“构造”线段bc。
(2)“构造”线段bc的中点作垂直平分线交直线ac于p。
(3)选定c点和p点,单击菜单命令:【构造】→【轨迹(u)】二、由限定条件作椭圆的轨迹根据椭圆的标准方程:■+■=1(a>b>0)或■+■=1(a>b>0)可得其参数方程为■=cosα■=sinα或■=cosα■=sinα。
圆规的正确使用方法和技巧

圆规的正确使用方法和技巧
圆规是一种常用于尺规作图的工具,用于绘制圆或弦。
正确的使用方法如下:
1. 用量尺或量角器测量圆规两脚之间的距离,将其作为半径。
2. 将带有针的一端固定在一个地方,作为圆心。
3. 将带有铅笔的一端旋转一周,使其在纸上画出圆。
在使用圆规时,需要注意以下几点:
1. 圆规两脚之间的高度要一样。
2. 画圆的过程中圆规要稍微倾斜,使画出的圆的线条流畅。
3. 画圆的过程中带有针的一端 (即圆心) 不能移动。
4. 画圆的过程中两脚距离 (即半径) 不能改变。
此外,圆规还有一些使用技巧:
1. 如果需要绘制较小的圆,可以将圆规两脚之间的距离适当减小。
2. 如果需要绘制较圆的圆,可以将圆规针尖适当抬高,以便更加准确地定位圆心。
3. 在使用圆规绘制圆弧时,需要根据需要调整圆规两脚之间的距离和角度,以便绘制出正确的圆弧。
圆规的正确使用方法和技巧可以帮助更加准确地绘制圆或弦,提高工作效率。
圆规技巧高效学习方法绘制几何形的实用技巧

圆规技巧高效学习方法绘制几何形的实用技巧几何学是数学的一个重要分支,它研究空间和图形的性质以及它们之间的关系。
在几何学中,圆规是一种常用的工具,它能够帮助我们绘制精确的几何图形。
本文将介绍一些使用圆规的高效学习方法和绘制几何形的实用技巧。
一、学会使用圆规的正确姿势和技巧1. 握持圆规:正确握持圆规是使用它的第一步。
将手握住圆规的铅笔尺,手指放在铅笔尺的一侧,另一侧用手指支撑。
这样握持圆规时既能保持稳定,又能够方便地移动和控制。
2. 调整圆规的开口:为了绘制不同大小的圆或弧,需要调整圆规的开口。
将圆规的螺丝旋转,使两脚之间的距离达到所需的大小。
3. 保持圆规垂直:在使用圆规绘制圆或弧时,要保持圆规垂直于纸面。
这样可以避免图形变形和尺寸不准确的问题。
二、绘制基本几何图形的技巧1. 绘制圆:将圆规的一只脚固定在纸上,以此为中心,用另一只脚围绕圆心画圆。
2. 绘制直径:绘制直径时,需要先确定圆的中心,然后使用圆规绘制两个相对的切线,这两个切线的交点即为圆的直径。
3. 绘制半径:绘制半径时,从圆心沿着圆的边缘使用圆规延伸一段距离即可。
4. 绘制弧:绘制弧时,需要确定圆心、半径和弧度。
将圆规的一只脚固定在弧的一个端点上,用另一只脚围绕圆心画弧。
5. 绘制正多边形:绘制正多边形时,可以利用圆规和直尺相结合的方法。
首先绘制一个圆,然后使用直尺连接圆心和圆上的点,将圆分成相等的扇形,最后通过绘制扇形的边界连接相邻的点,即可绘制出正多边形。
三、利用圆规绘制几何形的实用技巧1. 绘制切线:绘制切线时,可以利用圆规的性质。
将圆规的一只脚固定在圆上的一点上,以该点为圆心,调整圆规的开口,使另一只脚刚好与圆相切,然后移动圆规,即可绘制切线。
2. 绘制正弦曲线:绘制正弦曲线时,可以利用圆规和直尺的组合。
首先在纸上绘制一个坐标轴,然后以某个点为圆心,使用圆规绘制正弦曲线上的多个点,再通过直尺连接这些点,就可以绘制出正弦曲线。
3. 绘制相似图形:绘制相似图形时,可以利用圆规的特点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.做垂直相交的2条直线,在上面确定A、B、C、D、O五个点,AB为长轴,CD为短轴,O为中心点
2.连接AC
3.以O为圆心,OA的长为半径画圆,交CD线于E点
4.以C为圆心,CE的长为半径画圆,交AC线于F点
5. 以A为圆心,AF的长为半径画圆
6. 以F为圆心,AF的长为半径画圆,两圆弧相交2点G、H
7.连接GH,交AB轴于O1点,交CD轴于O2点
8.以O为圆心,OO1的长为半径画圆,交OB于O3点
(为了避免太多字母看的晕,下面不必要的点就没有标注字母了)
9. 以O为圆心,OO2的长为半径画圆,交OB于O4点
10. 以O1为圆心,O1A的长为半径画圆
11. 以O3为圆心,O3B的长为半径画圆
12. 以O2为圆心,O2C的长为半径画圆
13. 以O4为圆心,O4D的长为半径画圆
最新文件仅供参考已改成word文本。
方便更改。
