水产的养殖与捕捞的数学模型
9.生物数学捕鱼模型

• 捕捞效应会使被食鱼增长,所以不正确的 治虫,会使害虫增加,而天敌减少。 • 学习本模型,使学生认识到,生物种群的 发展是有规律的,在没有人为的干扰情况下, 该种群是处于平衡状态的,这是生物种群 千百万年以来所保持的规律性。正确的理 解生态平衡的概念和在捕鱼——被捕鱼系 统中的捕鱼效应。 • 由捕鱼效应还可以得到一个启示,看问题 不能表面化。喷洒农药治虫本来是正确的
•
本内容的难点,在于理解一维系统平衡点 的稳定性概念。 二、Volterra模型:这是一个生态问题,研究 捕鱼与被捕鱼系统的生态变化。上世纪20 年代,意大利生物统计学家D’Ancona,在 统计第一次世界大战期间,亚德利亚海中 被食鱼和鲸鲨鱼(掠肉鱼)比数的奇异变 化。在捕鱼减少的情况下,鲨鱼的比数意 外的上升。(鲨鱼比例为何如此上升?) 他让数学家Volterra把这一生态现象给以科 学的解释。
N N 故最大捕捞量为 m x0 2 2 4
二、Volterra模型 • 2.1问题的提出:1924年,意大利生物统计 学家Dancona在作生物统计工作是发现这 一问题。 • 在阜姆对亚德利亚海中的两种鱼的数量进 行统计。对捕获的鱼的种类及数量进行记 录。 • 他把鱼分成两种:鲨鱼,被食鱼,作为一 个捕食者——被捕食者系统。
•
Volterra通过建立捕鱼与被捕鱼系统模型, 科学的解释D’Ancona提出的问题。 • 1.在一个捕鱼被捕鱼系统中,如果没有外部 因素干与,两个种群的数量都按周期变化, 周期相同。这种现象就是生态平衡。 • 2.如果有人为干扰(即有捕捞时),捕捞可 增加被食鱼,减少鲨鱼,即会使被食鱼的 比数增大。此称为捕捞效应。
模型九、生物数学模型
这部分讲述两个模型: 一、 捕鱼模型 二、 Volterra模型 一、 捕鱼模型:在鱼类增殖的情况下进行捕 捞,研究捕捞系数多大时,鱼类增殖是稳 定的,并研究在稳定增殖情况下的最大捕 捞量。 学习该模型的目的,使人们认识到:为 了保护鱼类资源,实现可持续发展战略。 捕捞应有一定限制(如休渔期的规定), 以免过渡捕捞破坏渔业资源。
第十一章海洋渔业资源的科学管理

得:f = fMSY =a / 2b=r B∞ / 2q,MSY = a2 / 4b= r B∞2 / 4 只要算得参数a、b就可计算得MSY及其相应的fMSY
4、参数估算
(1)f 标准化:用于当量计算
标准船、作业时间、网次
(2)估算
原理:根据平衡状态下单位捕捞力量渔获量与捕捞力量为线性关系,进行直线回归
是最大持续产量MSY。
(三)鱼类的生长
1、经验公式: 伯塔兰菲(Von Bertalanffy)体重增长方程式可表示
为:
Wt = W∞ 〔1―e―K ( t - t 0 ) 〕3
• Wt:年龄t的平均体重;曲线的曲率,决定趋向W∞的变动率的一个常数; • t0:体重为零时的理论年龄,小于零。
c p
a
n
平衡渔获量 Y 平衡渔获量 Y
b
0
捕捞力量 f
图 11.2 不同种类的总渔获量
和捕捞力量的关系
m
0
捕捞力量 f
图 11.3 同一种类不同网目的捕捞力量
和总渔获量的关系
(三)过度捕捞(overfishing)
如果捕捞量超过种群本身的自然增长能力,将导致资源 量不断下降,表现在总渔获量和单位捕捞力量渔获量随捕捞 力量的增加而减少,同时捕捞对象的自然补充量也不断下降, 引起资源衰退(甚至最终形成不了渔汛) 。 生物学捕捞过度:
表明在平衡状态下,平衡渔获量与捕捞力量亦呈抛物线关系。
设 a = q B∞ , b = q2 B∞/ r
即 Y =a f -b f 2
或 Y / f= a — bf
表明平衡状态下,单位捕捞力量渔获量与捕捞力量为线性关系。
3.MSY与fMSY 由Y = a f -b f 2求Y最大值,须令 dY /df = a — 2bf =0
从几个生活实例看数学建模及其应用

从几个生活实例看数学建模及其应用[内容摘要] 本文通过几个生活中的事例,并运用数学建模,来分析问题,以便更方便的得出解决问题的方案。
从中通过将数学建模的抽象理论实例化,生动化,我们能够更清楚看出数学在生活中无处不在,无处不用。
[关键词] 数学建模生活数学数学,作为一门研究现实世界数量关系和空间形式的科学,与生活是息息相关的。
作为用数学方法解决实际问题的第一步,数学建模自然有着与数学相当的意义。
在各种不同的领域中,人们一直在运用数学建模来描绘,刻画某种生活规律或者生活现象,以便找到其中解决问题的最佳方案或得到最佳结论。
例如,运用模拟近似法建模的方法,在社会科学,生物学,医学,经济些学等学科的实践中,来建立微分方程模型。
在这些领域中的一些现象的规律性仍是未知的,或者问题太过复杂,所以在实际应用中总要通过一些简化,近似的模型来与实际情况比对,从而更加容易的得出规律性。
本文通过数学模型在生活中运用的几个例子,来了解,探讨数学模型的相关知识。
一、数学模型的简介早在学习初等代数的时候,就已经碰到过数学模型了,例如在三个村庄之间建立一个粮仓,使其到三个村子的距离只和最短。
我们可以通过建立方程组以及线性规划来解决该问题。
当然,真实实际问题的数学建模通常要复杂得多,但是建立数学建模的基本内容已经包含在解决这类代数应用题的过程中了。
那就是:根据建立模型的目的和问题的背景作出必要的简化假设;用字母表示待求的未知量;利用相应的物理或其他规律,列出数学式子;求出数学上的解答;用这个答案解释问题;最后用实际现象来验证结果。
一般来说,数学模型可以描述为,对于现实世界的一个特定对象,为了一个特定目的,根据特有的内在规律,作出一些必要的简化假设,运用适当的数学工具,得到的一个数学结构。
二、数学模型的意义1)在一般工程技术领域,数学建模仍然大有用武之地。
2)在高新技术领域,数学建模几乎是必不可少的工具。
3)数学迅速进入一些新领域,为数学建模开拓了许多新的处女地。
保持捕鱼业持续收获的Compertz模型

第2 卷第2 0 期
2 0 年 5月 0 8
宁德师专学报 ( 自然科 学版 )
Ju a o Nnd ec e C r g ( a r cec ) or l f igeT ah  ̄ oee N t a Sine n t ul
V0. 0 No 2 12 . Ma 0 8 y2 0
关键词 :o et模 型 ; C mpr z 平衡 点 ; 稳定解 中图分类号 : 7 . 5 S9 3 1 文献标识码 : A 文 章编号 :0 4—2 1 ( 08 0 10 9 12 0 )2—0 8 2 10—0
记时刻 t 场 中鱼 量为 ( ) 关 于 () 自然 增 长和 人工 捕捞 作 如下假 设 : 渔 t, t的 1 在无 捕 捞条件 下 ( ) 。 t 的增 长 服从 C m et模 型 , o pr z 即
的捕捞 量 为
hx = = x ( ) E () 2
根 据 以上假设 并 记
V( )= )一 ( ) 得 到 捕捞 情况 下 渔 场鱼量 满足 的方 程 x hx ,
d 加 譬 E x 一 x
点并分 析其 稳定 性。 令 V( )=rl 一 x=0 得到 平衡 点 x xn E ,
E— i cj0 0 y a . e ma :sl 1 @ e I n t l 1
维普资讯
第 2期
蔡述健 : 保持捕鱼业持续 收获的 C m e z o pr 模型 t
・l l・ 8
根据假设 2 P点的纵坐标 ^为稳定条件下单位时 ,
间 的持续 产 量 , 由上 图立刻得 知 , Y=E 当 x与 Y: ) 在 曲线 顶点 Q相 交时 可获 得最 大 的持 续 产 量 , 时 的稳 定 此 平衡 点 为
捕渔模型

鱼群再生产曲线及最大可持续捕获量一、摘要本文基于对鱼群再生产以及捕捞的可持续性假设,通过对鱼群生长以及捕捞规律的分析研究,利用微分——差分和数据拟合建立了鱼群生态系统的预测模型。
针对鱼群的再生产情况,我们分别对无阻滞增长和阻滞增长进行分析比较。
我们定义自然增长率r ,鱼的均重M ,对于无阻滞增长rt e y =,可知鱼群的再生产与时间成正比无限增长,该模型不符合现实。
针对阻滞增长模型,我们又假设其最大环境容纳量N ,根据)1(N y ry dt dy -=作出dtdy 与t 的图像,再根据t- e )1(1)(r N x N t y -+=, 用数值拟合方法得出S 形曲线。
原题的要求以一年为周期计算鱼群的再生产曲线,因此我们用周期作为时间段来研究鱼群的增长规律比用连续时间方便。
将)1(Ny ry dt dy -=转化为差分方程并得到)1(x bx y -=。
由图可知,鱼群第二年的产量围绕N x =上下波动。
针对鱼群的可持续捕捞情况,我们分别对固定量捕捞和固定努力量捕捞进行分析比较。
针对固定量捕捞,定义固定捕捞量H ,在题一的基础上,建立函数关系式H x bx y --=)1(并得出图像,观察图像可知固定量捕捞难以达到最大量和持续捕捞的平衡。
对固定努力量捕捞,定义了捕捞强度系数E,建立函数关系式Ex x bx y --=)1(,用数值拟合的方法作出)1(x bx y -=与Ex y =的图像,找出一个合适的捕捞率,并在此捕捞率的基础上找出最适鱼群数量。
当Ex y =与)1(x bx y -=交于顶点时,达到最大持续产量,此时的稳定平衡点为2N x =,即将捕捞后的鱼群产量控制在2N x =,可获得最大持续捕获量。
综上所述,我们认为我们建立的数学模型易于操作,对实践有着较好的指导意义。
关键词:再生产 微分——差分 S 形曲线 抛物线最大持续捕获量 阻滞增长模型二、问题重述鱼群是一种可再生资源,若目前鱼群的总数为x公斤,经过一年的成长与繁殖,第二年鱼群的总数变为y公斤。
(完整版)数学模型(第四版)课后详细答案
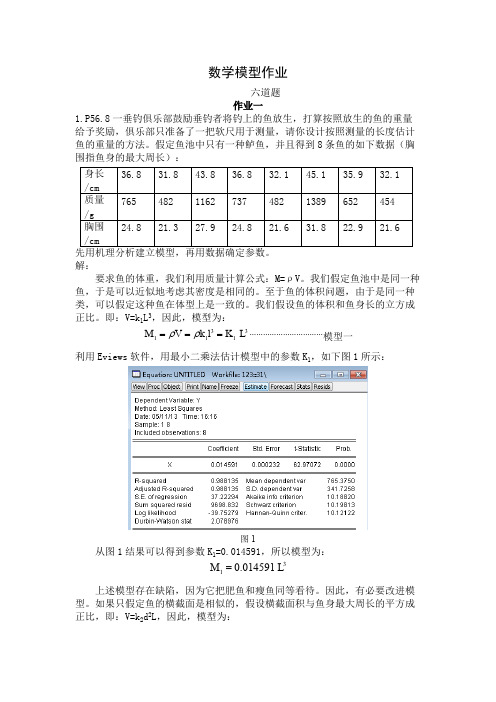
数学模型作业六道题作业一1.P56.8一垂钓俱乐部鼓励垂钓者将钓上的鱼放生,打算按照放生的鱼的重量给予奖励,俱乐部只准备了一把软尺用于测量,请你设计按照测量的长度估计鱼的重量的方法。
假定鱼池中只有一种鲈鱼,并且得到8条鱼的如下数据(胸围指鱼身的最大周长):先用机理分析建立模型,再用数据确定参数。
解:要求鱼的体重,我们利用质量计算公式:M=ρV。
我们假定鱼池中是同一种鱼,于是可以近似地考虑其密度是相同的。
至于鱼的体积问题,由于是同一种类,可以假定这种鱼在体型上是一致的。
我们假设鱼的体积和鱼身长的立方成正比。
即:V=k 1L 3,因此,模型为:……………………………模型一33111M V k l K L ρρ===利用Eviews 软件,用最小二乘法估计模型中的参数K 1,如下图1所示:图1从图1结果可以得到参数K 1=0.014591,所以模型为:31M 0.014591 L =上述模型存在缺陷,因为它把肥鱼和瘦鱼同等看待。
因此,有必要改进模型。
如果只假定鱼的横截面是相似的,假设横截面积与鱼身最大周长的平方成正比,即:V=k 2d 2L ,因此,模型为:身长/cm 36.831.843.836.832.145.135.932.1质量/g 76548211627374821389652454胸围/cm24.821.327.924.821.631.822.921.6t h i ng sin………………………………模型二22222M V k d K d L L ρρ===利用Eviews 软件,用最小二乘法估计模型中的参数K 2,如下图2所示:图2从图2可以得到参数K 2=0. 032248,所以模型为:22M 0.032248d L=将实际数据与模型结果比较如表1所示:表1实际数据M 76548211627374821389652454模型一M 1727.165469.2141226.061727.165482.6291338.502675.108482.619模型二M 2729.877465.2481099.465729.877482.9601470.719607.106483.9602.P131.2 一家出版社准备在某市建立两个销售代理点,向7个区的大学生售书,每个区的大学生数量(单位:千人)已经表示在图上。
水产养殖中的养殖规模与产值预测方法

水产养殖中的养殖规模与产值预测方法水产养殖作为一种重要的农业产业,对于国民经济的发展和人们的生活有着不可忽视的影响。
在水产养殖中,了解和预测养殖规模及产值是制定合理经营策略和决策的关键。
本文将探讨水产养殖中的养殖规模与产值预测方法,帮助养殖业者进行经营管理。
1. 养殖规模预测方法养殖规模预测是指对未来一定时期内水产养殖的规模进行合理的估计和预测。
在实际操作中,可以采用以下方法进行养殖规模的预测:1.1 经验法经验法是养殖业者根据自身多年的经验和观察,在一定程度上对养殖规模进行预测。
通过积累养殖经验,可以根据过往养殖规模和收益情况,结合市场需求和资源可利用情况,对未来的养殖规模作出合理估计。
然而,由于经验法依赖于个体经验,存在一定的主观性和局限性。
1.2 趋势法趋势法是指通过对历史数据进行趋势分析,推测未来养殖规模的变化趋势。
可以通过统计分析和回归预测等方法,分析养殖规模与相关因素(如市场需求、资源供给等)的关系,进而预测未来的养殖规模。
趋势法相对于经验法更加客观,但仍然依赖于历史数据的准确性和对趋势的合理判断。
1.3 模型法模型法是一种利用数学或经济模型来预测养殖规模的方法。
通过建立养殖规模与各种影响因素之间的数学模型,可以对未来的养殖规模进行预测和优化。
常用的模型包括生产函数模型、供需平衡模型等。
模型法具有科学性和客观性,但需要根据具体情况选择和建立适用的模型。
2. 产值预测方法产值预测是指对水产养殖产出的经济价值进行合理估计和预测。
在进行产值预测时,可以考虑以下方法:2.1 边际收益法边际收益法是通过对养殖单位产量增加所带来的额外收益进行预测。
通过计算每单位养殖规模(如每亩、每头等)所带来的产值,结合养殖规模的预测,可以估计未来的产值。
边际收益法直观简单,适用于规模较小的养殖场。
2.2 面积法面积法是根据水产养殖的实际面积和单位面积产值进行预测。
通过对养殖区域的面积扩大或缩小进行预测,结合单位面积产值的变化趋势,可以估计未来的产值。
数学模型(第四版)课后详细答案
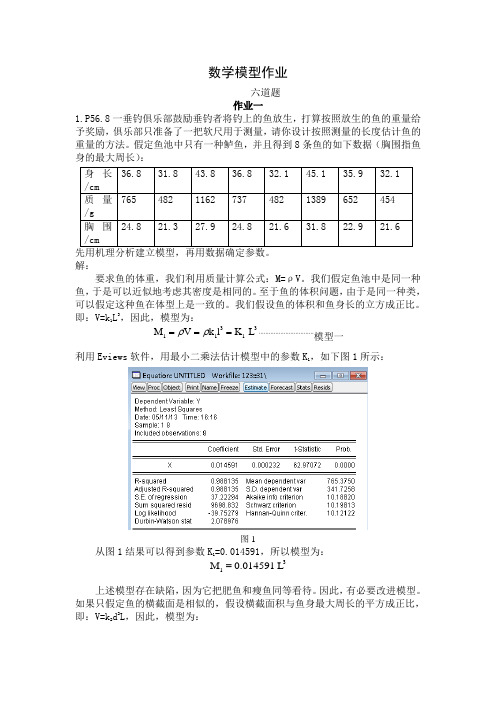
数学模型作业六道题 作业一1.P56.8一垂钓俱乐部鼓励垂钓者将钓上的鱼放生,打算按照放生的鱼的重量给予奖励,俱乐部只准备了一把软尺用于测量,请你设计按照测量的长度估计鱼的重量的方法。
假定鱼池中只有一种鲈鱼,并且得到8条鱼的如下数据(胸围指鱼身的最大周长): 解:要求鱼的体重,我们利用质量计算公式:M=ρV 。
我们假定鱼池中是同一种鱼,于是可以近似地考虑其密度是相同的。
至于鱼的体积问题,由于是同一种类,可以假定这种鱼在体型上是一致的。
我们假设鱼的体积和鱼身长的立方成正比。
即:V=k 1L 3,因此,模型为:33111M V k l K L ρρ===……………………………模型一 利用Eviews 软件,用最小二乘法估计模型中的参数K 1,如下图1所示:图1从图1结果可以得到参数K 1=0.014591,所以模型为:31M 0.014591 L =上述模型存在缺陷,因为它把肥鱼和瘦鱼同等看待。
因此,有必要改进模型。
如果只假定鱼的横截面是相似的,假设横截面积与鱼身最大周长的平方成正比,即:V=k 2d 2L ,因此,模型为:身长/cm36.8 31.8 43.8 36.8 32.1 45.1 35.9 32.1 质量/g765 482 1162 737 482 1389 652 454 胸围/cm24.8 21.3 27.9 24.8 21.6 31.8 22.9 21.622222M V k d K d L L ρρ===………………………………模型二利用Eviews 软件,用最小二乘法估计模型中的参数K 2,如下图2所示:图2从图2可以得到参数K 2=0. 032248,所以模型为:22M 0.032248d L=将实际数据与模型结果比较如表1所示:表1实际数据M765 482 1162 737 482 1389 652 454模型一M 1 727.165 469.214 1226.061 727.165 482.629 1338.502 675.108 482.619 模型二M 2 729.877 465.248 1099.465 729.877 482.960 1470.719 607.106 483.9602.P131.2 一家出版社准备在某市建立两个销售代理点,向7个区的大学生售书,每个区的大学生数量(单位:千人)已经表示在图上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
水产的养殖与捕捞的数学模型欧杰泉(1) 柯文锋(2) 赖金花(3)(1)韶关学院2000级数学系数学与计算机教育6班(2)韶关学院2000级数学系数学与应用数学本科1班(3)韶关学院2000级计算机系计算机科学与技术本科1班(广东省韶关学院,韶关,512005)摘要:由单位时间虾的增长量,单位时间虾的捕捞量,单位时间虾的死亡数,构造一个函数,利用求函数的导数的方法,求出此函数的平衡点,对问题1 ,列出单位时间的利润函数,并把以上的平衡点代入此单位时间的利润函数中,此单位时间的利润函数是捕捞系数的二次函数,再次利用求函数的导数的方法,求出此函数的稳定点,由实际问题得知此稳定点是单位时间利润函数的最值点,此时利用养殖场中每月虾量相等条件,即单位时间虾的捕捞量与单位时间虾的死亡数之和等于单位时间虾的增长量,即可确定捕捞策略(E=0.0885),得到每月养殖的虾量x=3075斤和最大利润R=1398.82元;对问题2,列出5年的总利润a 的函数,利用计算机Maple 软件求函数的字的最大值来确定a 值,求得a=0.3006.当初始条件为x=1000时,获得最大利润下的虾场稳定虾量R x =5313.19,求出第(t ≈11.3677)月开始捕捞能使获得利润最大82398.938元.对问题3,列出5年的总利润关于y 的函数,即可求获得最大利润下的虾场稳定的虾量R x =5497.75,以及最大需要的月养殖费y=1831.67元. 关键词:稳定点,捕捞系数,平衡点.1 问题的提出韶关市某人工养殖的水产业(如养殖场中的养殖),其产量的增加一般与养殖费(包括饲料、工资、技术费等)成正比。
而当养殖场虾量达到养殖场最大允许虾量时,养殖费投入再大也不会使虾量增加。
但若不投入养殖费,养殖场中的虾将会慢慢死去。
现考虑养殖场中某种虾的养殖与固定努力量捕捞。
用x(t)表示养殖场中第t 月的虾量(单位:斤),用y(t)表示第t 月的月养殖费(单位:元/月),根据以往经验和市场调查,我们有如下数据:*这种虾的自然死亡率为λ,λ=0.05(1/月);*环境容许的最大虾量为410,=N N (斤);*在无捕捞和自然死亡的情况下,养殖场虾量x(t)的增加速度与月养殖费y(t)成正比,其比例系数是x(t)的函数;当x(t)达到N 时,此函数为0,当x(t)为0时,此函数为常数αα,=1(斤/元);*虾的捕捞采用拉网式固定努力量捕捞,即每月的捕捞量与此时养殖场虾量x(t)成正比,比例系数为E 。
这种拉网式捕捞每次捕到的虾中出现小虾、中虾、大虾的概率分别为0.2、0.5、0.3,而捕捞成本为ββ,=0.1(元/斤);小虾、中虾、大虾平均每斤的批发价格分别为5元,7元和10元。
1.人长期承包这养殖场,要求养殖场中每月的虾量都相等,且月养殖费y(t)与该月虾量x(t)成正比,比例系数为αα,=0.2(元/斤*月)。
试指定捕捞策略(确定E ),使虾的月利润最大,此时每月养殖场的虾量及利润各是多少?2.若某人承包次养殖场5年,且养殖费y(t)与该月虾量x(t)成正比,比例系数为a ,又取E=0.08(1/月)。
试制定养殖策略(确定a ),使5年的总利润最大。
如果初始虾量为310斤,那么使获利最大的开始捕捞的月份是多少?3.若某人承包此养殖场5年,每月按强度E=0.1(1/月)捕捞,试制定养殖场策略(确定养殖费y(t)),使5年的总利润最大。
2 问题的分析本题有三个问,对第一问,是在养殖场中每月的虾量相等条件下,即单位时间虾的捕捞量与单位时间虾的死亡数之和等于单位时间虾的增长量,求单位时间的利润函数的最值问题;对第二问,总利润函数是a 的函数,利用计算机Maple 数学软件使得总利润函数取得到最大值,确定a 值把E 的值代入x 的平衡点,即获得最大利润下的虾场稳定虾量R x 的关系,即可以知那个月开始捕捞能获利最大;对第三问,总利润函数是y 的函数,利用Maple 数学软件可求得获得最大利润下的虾场稳定虾量R x 以及最大需要的月养殖费。
3 模型假设1.养殖场不与其它水域发生关系,是一个独立的生态群落。
2.虾群是一个独立的种群,在此虾群的生态群落中,没有其它种群。
3.所有造成虾死亡的因素都在虾的自然死亡率之内。
4. 虾的捕捞都能销售,也就是说打捞的虾都能卖出,且价格保持不变,销售成本费用忽略不计。
5. 捕捞的虾都能销售,也就是说打捞的虾都能卖出,且价格保持不变,销售成本费用忽略不计。
6. 在无捕捞和自然死亡的情况下,养殖场虾量x(t)的增长速度与月养殖费y(t)成正比,其比例系数是x(t)的线性减函数:P(x(t))=A-Bx(t).4 符号约定r 是固定增长率; N 是环境容许的最大虾量;h(x)是单位时间的捕捞量; y(t)是单位时间的养殖费;w(t)是单位时间; p 是虾销售单价的数学期望;T 是单位时间收入; S 是单位时间的去出;R 是单位时间的利润; λ是虾的自然死亡率;E 是捕捞强度系数; β是捕捞成本;5 月利润最大的数学模型的建立和求解自然死亡规律:)()(t x dtt dx λ-= 捕捞模型:)()(t Ex dtt dx -= P(x(t))=A-Bx(t), 由假设(6)可知: 当x(t)=N 时,P(x(t))= a .解得:A=a ,B=N α.p(x(t))=))(1(Nt x -α. 在捕捞和自然死亡的情况下,养殖场虾量随时间变化的数学模型:)()()())(1()(t x E t y Nt x dt t dx +--=λα ……(1) 在每月的虾量相等条件,确定捕捞策略(确定E ),使虾的月利润最大: 每月的虾量相等条件()0=⇔dtt dx()()()()01=+-⎪⎭⎫ ⎝⎛-⇔t x E t y N t x λα 由假设可知: ()()t ax t y = ()()()()01=+-⎪⎭⎫ ⎝⎛-⇔t x E t ax N t x λα 解得: 01=x (舍去) ()αλαa E a N x --=2 ——(2) 称(1)式得平衡解 月养殖费()()ax t ax x y ==月捕捞成本费()()Ex t h t w ββ==单位时间收入T 和成本S 分别为:T =Ex p Ex p Ex p 332211ξξξ++S =y(t)+W(t)=ax+βEx每月利润=价格×捕捞量—成本—月养殖费。
每月虾量相等的最大利润捕捞模型为:R=T —S =Ex ax Ex p Ex p Ex p βξξξ--++332211s.t ()()∂--=a E a N t x λαλα-<a E 332211ξξξp p p p ++==++=332211ξξξp p p p 5×0.2+7×0.5+10×0.3=7.5模型的求解 ()()a Ea N a E pE E R αλαβ----=()a pEE a N a E a N p dE dR αβαλαβ-++---=令0=dE dR, 求得稳定()()βλα-+-=p aa E 2210由实际情况可知: 0E 是最大值点把p=7.5,β=0.1,a =0.2,λ=0.05,α=1,N =410捕捞强度为0885.00≈E (1/月)每月养殖场最大虾量 30750≈--=a Ea N x αλα(斤)最大月利润()82.13980≈E R (元)6 承包五年捕捞强度E =0.08(1/月)的养殖策略的模型建立和求解1) 此时的数学模型(二)为:()()dt Ex ax pEx a R ⎰--=600m ax β s.t. ()()()()t X E t X N t X a dt dx +-⎪⎭⎫ ⎝⎛-=λα1 2) 上述微分方程的解为()()()()t E a e ax EN N aN ax E a N x t x ------+--=λααλααλα0003) 求解方法 将上述()t x 代入目标函数R (a )中,并利用积分公式:()⎰⎥⎦⎤⎢⎣⎡+-+=+---216060213121ln ln 1333C C e e C C C C e C C dt C C t C 对R (a )的解析式关于a 求导,并令()0=da a dR ,再确定R (a )的最值。
(求解过程用Maple 软件进行)。
4) 结果p=7.5,β=0.1,λ=0.05,α=1,N =410,E =0.08得 a ≈0.3006239887(元./月 斤)养殖场虾量水平为5313.19(斤);5年的最大利润为82398.93829(元)。
5) 当x (0)=310时,获利最大的开始捕捞时间 ()()()()t a e a N aN a a N t x λααλααλα----+-=333101010 将N =410,()19.5313,05.0,2774.0===t x λα 代入上式,解得 t ≈11.3677(月)≈341(天)即当初始虾量为310斤始,获利最大的开始捕捞的月份11.4月。
7 承包5年捕捞强度E =0.1(1/月)得一般养殖策略的模型建立和求解1. 数学模型(三)()()()()[]⎰-=60074.0max dt t y t x t y RS .T . ()()()()t x t y t x dt t dx 15.01014-⎪⎭⎫ ⎝⎛-=2. 用变分法求解上述泛函极值: 令()()()()()()()⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛-+-=t x t y t x t u t y t x y x t H 15.010174.0,,4 则由欧拉方程得下转接17页。
