多维非稳态对流扩散问题分析
一维非稳态对流-扩散方程的隐式中心差分格式

一维非稳态对流-扩散方程的隐式中心差分格式一维非稳态对流-扩散方程描述了在一维空间中同时存在对流和扩散过程的物理现象。
这个方程在很多工程和科学领域都有广泛的应用,如热传导、质量传输和流体力学等。
对方程进行数值求解可以得到物理现象的定量解,进而对系统行为进行预测和优化。
对于一维非稳态对流-扩散方程的数值解法中,中心差分格式是一种常用的方法。
中心差分格式是基于中心差分近似的方法,该方法精确地处理了对流和扩散效应,并适用于广泛的问题。
其中,隐式格式是一种特殊的中心差分格式,它在处理高度非稳态情况下的数值解具有优势。
在一维非稳态对流-扩散方程的隐式中心差分格式中,我们假设空间网格的节点为x_i,时间步长为Δt。
方程的解u(x,t)在网格节点x_i处的近似值为u_i^n,其中n表示时间步数。
根据对流和扩散项的中心差分近似,方程可以离散为如下的格式:(u_i^{n+1}-u_i^n)/Δt=α(u_{i-1}^{n+1}-2u_i^{n+1}+u_{i+1}^{n+1})/(Δx^2)-β(u_{i+1}^{n+1}-u_{i-1}^{n+1})/(2Δx)其中,α表示扩散系数,β表示对流系数,Δx表示空间步长。
在隐式中心差分格式中,时间步n+1的解u_i^{n+1}是未知的,我们将其视为待求解的值。
通过将方程的右侧扩散和对流项全部取为n+1步的值,从而得到一个关于u_i^{n+1}的线性方程。
因此,我们可以得到如下的表达式:u_i^{n+1}=(αΔt/(Δx^2)-βΔt/(2Δx))u_{i-1}^{n+1}+(1-2αΔt/(Δx^2))u_i^{n+1}+(αΔt/(Δx^2)+βΔt/(2Δx))u_{i+1}^{n+ 1}这个方程可以用矩阵的形式表示为:AU^{n+1}=BU^n其中,U^{n+1}是一个列向量,包含了所有网格节点i处的解u_i^{n+1};U^n是一个列向量,包含了所有网格节点i处的解u_i^n;A和B是相关系数矩阵,具体的表达式为:A=[1-2αΔt/(Δx^2),αΔt/(Δx^2)+βΔt/(2Δx),0, 0[αΔt/(Δx^2)-βΔt/(2Δx),1-2αΔt/(Δx^2),αΔt/(Δx^2)+βΔt/(2Δx), 0[0,αΔt/(Δx^2)-βΔt/(2Δx),1-2αΔt/(Δx^2), 0...[0,...,0,αΔt/(Δx^2)-βΔt/(2Δx),1-2αΔt/(Δx^2)]B = identity matrix通过求解这个线性方程组,就可以得到隐式中心差分格式下的数值解。
非稳态扩散名词解释

非稳态扩散名词解释
非稳态扩散:一种“活跃”的化学扩散
在微观层面上,物质扩散体现为分子、原子或颗粒在不断变化的温度和压力的
作用下,穿过物质中的液体、气体,或者在它们的表面上的不断运动。
扩散,也可以在物理或化学上被描述为一种“运动”,而其中物质在运动过程中发生变化。
综上所述,扩散是宏观层面上和微观层面上不可缺少的一种运动过程。
在物理学中,扩散分为稳态扩散和非稳态扩散两类。
非稳态扩散是一种“活跃”的化学扩散,它会对它所经过部位的物态和选择性
形成一定的影响。
非稳态扩散过程中所演变出的物质的特性和空间散布情况反映出来,它的动力学特性一般由粒子的时空变化表征。
非稳态扩散一般不受外力的影响,它比一般的扩散更加活跃,所以在物质的多种化学活动中,它都起着重要的作用。
此外,非稳态扩散特别常见于微小体系,其会受到表面能和粒子相互作用的影响。
非稳态扩散比起稳态来说有较大的自主性,它能够更有效地传播激发信号,在传输消息中起到重要的作用。
它可以被用来驱动多时间尺度短、热休克信号跳跃或复杂化学反应等现象,发生在不稳定的体系中。
总而言之,非稳态扩散是一种多变现象,先于某一物质的变化而发生,而它的
演变轨迹由粒子的时空变化所誊描,它的影响力充满多样性,因为它可以驱动过多个时间尺度复杂的化学变化现象。
未稳态扩散可以说是化学活动中要有的不可缺
少的部分,它所提供的经历可以帮助研究者更深入地分析和预测化学系统的运行及其复杂程度。
CFD理论对流项与扩散项

CFD理论对流项与扩散项《数值计算》导读:介绍离散方程中对流项及扩散项的物理特性,分析离散方程的迁移性。
01物理过程从物理过程的角度,对流与扩散现象在传递信息或扰动方面的特性有很大的区别。
扩散是由于分子的不规则热运动所致,分子不规则热运动对空间不同方向几率都是一样,因此扩散过程可以把发生在某一地点上的扰动的影响向各个方向传递。
对流是流体微团的定向运动,具有强烈的方向性。
在对流作用下,某一地点扰动的影响只能向其下游方向传递而不会逆向传播。
在离散过程中,对流和扩散的物理特性可以在各自的离散格式中体现出来。
02扩散项的中心差分扩散项的离散格式要求能够满足将扰动向四周均匀传递的特性。
这里,我们以一维非稳态扩散方程为例:其中心差分的显示格式:采用离散扰动分析法来确定上式传递扰动的特性。
假设开始的物理量的场已经均匀化,即处处相等,且假定其值为零;从时刻开始,在节点突然有一个扰动,而其余各点的扰动都为零,如下图所示。
将上诉的中心差分格式应用于时层的的各个节点。
对于节点:其中:,可以得到:对于节点:其中:,可以得到:对于节点:如果取,则时层的扰动到时刻变成下图所示: :显然时刻发生在节点的扰动已均匀向四周传递。
因此扩散项的中心差分格式具有使扰动均匀地向四周传递的特性,并且具有守恒性。
03对流项的差分格式首先要提到迁移性,如果某种离散格式仅能使扰动沿着流动方向传递,则说明此格式具有迁移特性。
我们以一维纯对流方程的非守恒形式为例:运用离散扰动分析法。
中心差分格式将中心差分格式运用于上式:采用第二节类似的方法,对于节点在时层:而在点处:可以看出,点的扰动可以同时向相反的两个方向传递,所以对流项的中心差分具有迁移特性。
迎风差分格式迎风差分格式的基本思想是迎着来流(即上游)去获取信息以构造的离散格式。
本文采用Taylor展开法中迎风差分的构造方法。
上式为点一阶导数的向后或向前差分,因为只有一阶截差,因而称为一阶迎风格式。
非稳态扩散名词解释

非稳态扩散名词解释非稳态扩散是指物理、材料、化学及生物系统中的扩散过程,它对应于热力学的熵的非稳态增加。
它的本质是物质或能量从一个地方向另一个地方转移,以满足不均衡态的需要和条件。
而且它还可以在某些情况下产生有益的结果,从而改善系统的性能和功能。
非稳态扩散涉及一系列不同的现象,如传热、传热和传质等。
扩散在热力学中是指物质穿过温度或其他物理变量时,将温度或其他物理变量不均匀分布于各处的过程。
热扩散可以在物体表面和内部之间传递热量,而扩散系数描述的是热传递的强度。
扩散过程的速率取决于物质的种类、浓度和热能等。
热扩散是通过物体温度从高温区至低温区的传热而实现的,它对于定义散热器的有效性至关重要。
传质扩散是指在不同区域之间物质的扩散过程,即使温度在整个系统中是均衡的,也可以发生物质的扩散。
传质扩散的驱动力是物质的溶质浓度差异。
当物质的浓度在某一位置大于其他位置时,物质就会从高浓度区域流向低浓度区域。
这种可能会导致不良的影响,如污染和气味的扩散,因此应该尽可能多地阻止传质扩散。
生物系统中的非稳态扩散是指物质或信息在生物体之间以及内部生物体内部的扩散。
在生物体之间,细胞间信号传导是一种重要的非稳态扩散过程,其涉及受体细胞、信号转导蛋白与接受信号的分子等,其中都包含扩散的本质。
生物体内部的非稳态扩散是指细胞的活性蛋白的扩散,涉及到细胞间质和细胞膜的传递,从而影响各种细胞活性及细胞内功能的分布。
从上述内容可以看出,非稳态扩散是一种普遍存在的物理现象,它可以发生在物理、材料、化学和生物系统中,对于系统的功能性和性能有着重要的影响。
非稳态扩散涉及不同的现象,包括热传导、传热和传质扩散,以及生物体内部的细胞间信号传导和细胞内蛋白的扩散。
因此,了解非稳态扩散的机制和其对系统性能影响的理解,对于提高材料或生物系统的效率以及可靠性具有重要的意义。
二维非稳态对流扩散方程反问题的混沌粒子群算法

二维非稳态对流扩散方程反问题的混沌粒子群算法陈亚文;邹学文【摘要】为了求解二维非稳态对流扩散方程的参数反问题,利用有限元方法给出其正问题的求解,将结果作为附加条件,结合混沌局部搜索算法的优点,提出了一种改进的混沌粒子群优化算法.数值模拟结果表明此方法所得到参数反演的数值解与真解误差很小,目标值达到10-4,精度较高.%In order to solve two-dimensional non-steady-state convection-diffusion equation of the parameters inverse problem, using the finite element method to give its positive question solution as additional conditions, and combining with the advantages of chaotic local search algorithm,an improved chaotic particle swarm optimization algorithm is proposed. The simulation result shows that the error between the numerical solution of parameter inversion and the true solution is very small, the target value is up to 10-4. The method has higher accuracy.【期刊名称】《西安工业大学学报》【年(卷),期】2011(031)005【总页数】4页(P470-473)【关键词】群体智能;对流扩散方程;混沌局部搜索;粒子群优化;反问题【作者】陈亚文;邹学文【作者单位】(西安理工大学理学院,西安710054;西安理工大学理学院,西安710054【正文语种】中文【中图分类】TP301.6对流扩散方程描述了物质传输及热传递的综合过程,在水利工程、环境工程及化工、冶金、航空等研究领域里受到了充分重视,因此对流扩散方程的数值求解一直是人们关注的问题之一[1-2].对于其反问题,一般都可归结为一类优化问题,此优化问题一般为多峰值高度非线性优化问题,如何进行有效求解引起了人们广泛重视. 群智能(Swarm Intelligence,SI)作为一种新兴的演化计算技术已成为越来越多研究者的关注焦点,它与人工生命,特别是进化策略以及遗传算法有着极为特殊的联系.群智能在没有集中控制且不提供全局模型的前提下,为寻找复杂的分布式问题求解方案提供了基础.目前,群智能理论研究领域有两种主要的算法,蚁群优化算法(Ant Colony Optimization Algorithm,ACOA)和粒子群算法(Particle Swarm Optimization,PSO).基于对鸟群、鱼群的模拟,Eberhart和Kennedy 于1995年提出粒子群优化算法.这些研究可以称为群体智能[3].PSO最初是处理连续优化问题的,目前其应用已扩展到组合优化问题.由于其简单、有效的特点,PSO已经得到了众多学者的重视和研究.Shi等提出了惯性因子w线性递减的改进算法,大大提高了基本PSO算法的性能.Vanden Bergh通过使粒子群中最佳粒子始终处于运动状态,得到保证收敛到局部最优的改进算法,但其性能不佳.Mendes等研究粒子群的拓扑结构,分析粒子间的信息流,提出了一系列的拓扑结构.Angeline将选择算子引入到PSO中,选择每次迭代后较好的例子并复制到下一代,以保证每次迭代的粒子群都具有较好的性能.文中采用PSO算法与有限元算法相结合的方法,给出了参数反演的数值结果,精度较高,表明算法的可行性和有效性.1 问题的提出考虑二维非稳态对流扩散方程当方程式(1)中的系数k(x,y,t),b1(x,y,t),b2(x,y,t),c(x,y,t),源项 f(x,y,t),初始条件φ(x,y),边界条件φ*(x,y,t)及常数σ为已知时,式(1)就构成了非稳态对流扩散方程的正演问题.假设 b1(x,y,t),b2(x,y,t),c(x,y,t),f(x,y,t),φ(x,y),φ*(x,y,t),σ及β(x,y,t)均为已知函数,再给出附加条件其中h(x,y,t)为已知函数,这样式(1)和式(2)便构成了反演系数k(x,y,t)的数学模型.2 求解方法考虑到h(x,y,t)只能在一些测量点得到,例如它们以T为采样周期,在t=iT (0,1,2,…,I)可以测量得到.并假设φi(x,y)是区域Ω上的基函数,并且令对于适当的n,以一组有限的基函数之和(x,y,t)来逼近k(x,y,t),则该类反问题为从已知的函数及附加条件来确定(x,y,t),由于基函数已定,确定(x,y,t)实际上是确定一个n维向量(a1,a2,…,an).令对应于(x,y,t)定解问题方程式(1)的解记为则反问题[4-5]便可转化为如下的最优化问题[6]ΓIt ={(x,y,t)∈ Γ1,t∈ [0,IT]},把式(3)作为粒子群算法[7]的适应值函数,适时调整参数a1,a2,…,an,使式(3)达到最小,那么就可得到k(x,y,t)的最优逼近解3 混沌粒子群算法混沌粒子群算法是混沌优化和粒子群优化两者的结合.对于给定的优化函数,通过将搜索过程对应为混沌轨道的遍历过程,可使搜索过程具有避免陷入局部极小的能力.将智能算法与经典算法相结合来构造一些高效的新的混合算法是目前解决优化问题的一个重要方向[8].文中的基本思想是采取混沌粒子群算法与有限元方法相结合求解二维非稳态对流扩散方程反问题,循环使用PSO算法与有限元方法,直到满足预定的优化目标为止. 混沌粒子群算法中涉及到混沌局部搜索算法(Chaotic Local Search,CLS),CLS的算法步骤为① 令k=0,将决策变量,j=1,2,…,n,按下式映射为0到1之间的混沌变量其中xmax,j和xmin,j分别为第j维变量的搜索上下界;② 计算下步迭代的混沌变量③ 将混沌变量转换为决策变量④ 根据决策变量对新解进行评价,若新解优于初始解X(0)=[,,…,]或者混沌搜索已达到最大迭代步数,将新解作为CLS的搜索结果,否则置k=k+1,转②.混沌搜索算法通常需要大量的迭代步数才可获得较好的解,且对初始解十分敏感,为了克服混沌搜索的缺点,将PSO算法与混沌搜索相结合,得到混沌粒子群算法.PSO算法只用于全局搜索,而CLS则根据PSO的结果进行局部搜索.混沌粒子群算法的步骤为① 设置当前参数,N为粒子数目;c1为学习因子1;c2为学习因子2;w为惯性权重;M为最大迭代次数;D为问题的维数;bound为位置的范围;v(i,j)为粒子的位置;xmax为自变量搜索域的最大值;xmin为自变量搜索域的最小值;maxC为混沌搜索的最大步骤.②随机初始化种群中各微粒的位置和速度.用下式初始化种群中各微粒的位置:③ 评价每个微粒的适应度,将当前各微粒的位置和适应值存储在各微粒的pbest 中,将所有pbest中适应值最优个体的位置和适应值存储于gbset中;④ 用下式更新每个微粒的速度和位置;⑤ 计算每个微粒的目标函数值,然后保留群体中性能最好的20%的微粒;⑥对群体中的最佳微粒执行混沌局部搜索,并更新其gbest及群体的gbest;⑦ 满足停止条件(通常为预设的运算精度或迭代次数),搜索停止,输出结果,否则转⑧;⑧ 按下面的式子收缩搜索区域其中xg,j为当前pbest的第j维变量的值;⑨ 在收缩后的空间内随机产生群体中剩余的80%的微粒,转③.在上面的混沌搜索的算法过程中,为了保持种群的多样性,加强搜索的发散性,在保留一定数量优秀微粒的同时,算法根据群体的最佳位置动态收缩搜索区域,并在收缩区域内随机产生微粒来替代性能较差的微粒.4 数值模拟数值模拟时,预先给出参数k(x,y,t)的真值,并求解正问题,计算出相应的附加条件,然后反求其参数.文中采用有限元法求解正问题.在单位矩形Ω=[0,1]×[0,1]上,考虑方程为时间采样分别取为t=0.2,t=0.5,即I=2,0<t<1,空间变量y的离散步长取为0.05.给定k(x,y,t),可通过有限元法求出u|x=1 =h(1,y,t),并把它作为附加条件.文中给定k(x,y,t)=5+3x+3y+5t.此时混沌粒子群算法的适应值函数可取为用a1+a2x+a3y+a4t逼近k(x,y,t),-6<ai <6,a1,a2,a3,a4 为反演参数,数值模拟中参数设置为N =60,c1=2,c2=2,w=0.8,M =200,D=4,xmax = 10*ones(1,4),xmin =-10*ones(1,4),maxC=100,模拟结果见表1.表1 参数反演结果Tab.1 Results of parameter inversion由表1的结果可以看出,利用混沌粒子群算法所得到参数反演的数值解与真解误差很小,说明文中算法在求解此类问题中是可行、有效的.5 结论文中在基本的粒子群算法的基础上,成功的将其与有限元方法相结合,在求解二维非稳态对流扩散方程反问题上显示了该算法的优越性,并且在数值模拟中也进一步说明了:文中提出的算法对偏微分方程反问题均适用,该算法可以更快、更稳定地收敛到问题的全局最优解.文中考虑的是对流扩散方程系数反问题,鉴于所提算法的良好的优化性能,下一步考虑将它应用到初始条件和边界条件反问题的求解中.【相关文献】[1]章争荣,张湘伟.对流扩散方程的数值流形格式及其稳定性分析[J].西安交通大学学报,2010,44(1):117.ZHANG Zheng-rong,ZHANG Xiang-wei.Numerical Manifold Scheme for Convection Diffusion Equation and Its Stability Analysis[J].Journal of Xi’an Jiaotong University,2010,44(1):117.(in Chinese)[2]陈翠霞,张小峰.求解一维对流扩散方程的一种新方法[J].武汉大学学报:工学版,2010,43(1):10.CHEN Cui-xia,ZHANG Xiao-feng.A New Solution to One-dimensional Convection-diffusion Equation[J].Journal of Wuhan University:Engineering Science Edition,2010,43(1):10.(in Chinese)[3]NATSUKI H.Particle Swarm Optimization with Gaussian Mutation[C]//In Proceedings of the IEEE Swarm Intelligence Symposium.Indianapolis,Indiana,USA,2003:72.[4]Dinh Nho Hào,Reinhardt H J.On a Sideways Parabolic Equation[J].Inverse Problems,1997,13(4):297.[5]Charles L,Karr I,Yakushin,K N.Solving Inverse Initial-value,Boundary-value Problems Via Genetic Algorithm[J].Engineering Applications of Artificial Intelligence,2000,13(6):625.[6]吴志健,康立山,邹秀芬.一种解函数优化问题的精英子空间演化算法[J].计算机应用,2003,23(2):13.WU Zhi-jian,KANG Li-shan,ZOU Xiu-fen.An Elitesubspace Evolutionary Algorithm for Solving Function Optimization Problems[J].Computer Applications,2003,23(2):13.(in Chinese)[7]魏静萱,王宇平.求解约束优化问题的改进粒子群算法[J].系统工程与电子技术,2008,30(4):739.WEI Jing-xuan,WANG Yu-ping.Smooth Scheme and Line Search Based Particle Optimization for Constrained Optimization Problems[J].Systems Engineering and Electronics,2008,30(4):739.(in Chinese)[8]袁益让,杜宁,王文洽,等.非线性多层渗流系统的数值方法及其应用[J].应用数学和力学学报,2006,27(11):1319.YUAN Yi-rang,DU Ning,WANG Wen-qia,etal.Numerical Method and Application for the Three-dimensional Nonlinear System of Dynamics of Fluids in Porous Media[J].Applied Mathematics and Mechanics,2006,27(11):1319.(in Chinese)。
二维非稳态对流扩散方程反问题的混沌粒子群算法

41 7
( ,)边界条件 ( , £ 及常数 为已知时 , z3 , , z , ) 式() 1 就构 成 了非稳 态对 流 扩散 方 程 的正演 问题 .
假 设 b( Y ,2z, ,( ,)f( Y,) lz, ,)b( ,)cx, £ , x, £ , ( ) ( Y,)a p x, ,)均 为 已知 函数 , z, , z, £ , ̄ ( Y 再给 出附 加条件 “I = h x, = ( Y,) = () 2
第 3 卷第 5 1 期 21 年 1 01 月 西安工
业
大
学
学
报
Vo. 1No 5 13 .
Oc. 0 1 t2 1
J u n l f ’n Te h oo ia iest o r a a c n lgc l o Xi Unv ri y
文章编 号 : 1 7 — 9 5 2 1 ) 54 00 6 39 6 (0 1 0 —7— 4
二维 非稳 态 对 流扩 散 方程 反 问题 的混 沌 粒子 群 算 法
陈亚 文,邹学文
( 西安 理工 大学 理学 院, 西安 70 5 ) 10 4
摘
要: 为了求解二维非稳 态对流扩散方程的参数反 问题 , 利用有限元方法给出其正问题的
求解 , 结 果作 为附加 条件 , 将 结合 混沌局部搜 索算 法的优 点 , 出 了一种 改进 的混 沌 粒子 群 优 提
,
群、 鱼群 的模 拟 , ehr Ebrat和 Ken d n ey于 19 95年
提 出粒子群 优化算法. 这些研究可 以称 为群体智
能[. S 3 P O最初是处理连续优化问题的, ] 目前其应 用 已扩展到组合优化 问题. 由于其简单 、 有效 的特
二维非稳态对流扩散边界控制问题的简化算法

第36卷第1期2019年3月经济数学JOURNAL OF QUANTITATIVE ECONOMICSVol.36,No.1Mar.2019二维非稳态对流扩散边界控制问题的简化算法”张国平,罗贤兵(贵州大学数学与统计学院,贵州贵阳550025)摘要针对二维非稳态对流扩散边界控制问题计算量大的问题,提出了基于降阶模型的最优实时控制方法.利用POD(the Proper Orthogonal Decomposition)和奇异值分解以及Galerkin投够方法得到了具有高精度离散形式的状态空间降阶模型.在所得的降阶状态空间模型中,利用离散时间线性二次调节器方法设计出了最优控制器.对沆一扩散过程的控制模拟结果说明了所提方法的有效性和准确性.关键词对流扩散边界控制问题;特征正交分解(POD);奇异值分解;降维模型中图分类号0242.1文献标识码AA Reduced Algorithm for Two-Dimensional UnsteadyConvective-Diffusion Boundary Control ProblemsZHANG Guoping,LUO Xianbing{School of Mathematics and Statistics,Guizhou University,Guiyang t Guizhou550025,China)Abstract Boundary control of two-dimensional unsteady convection diffusion is a large-scale optimization problem,and an approach was presented for optimal control based on reduced-order model,which was derived from a discrete-time low-order state-space model with high accuracy by using POD(the Proper Orthogonal Decomposition),singular value decomposition (SVD)and Galerkin projection.Optimal controllers were designed based on the low-order state-space models using discrete-time linear quadratic regulator(LQR)techniques.The controlling simulation results in the convection-diffusion process illustrate the effectiveness and accuracy of the proposed method.Key words convection-diffusion boundary control problem;the Proper Orthogonal Decomposition(POD);singular value decomposition;dimensionality reduction model1引言对流扩散方程所描述的最优控制问题山广泛应用于许多领域,如:大气污染控制问题,流体控制问题等,所以寻找稳定、高速实用的数值方法⑷,有着非常重要的实际意义.目前常用有限差分法⑷和有限元法⑷解决此类问题,然而一般情况下,大多数的差分格式和有限元格式计算量比较大,而且占用计算机内存多,特别是对于高阶的离散系统,其计算量将呈指数规律增长,计算成本将变得很大.因此,现在重要的问题是如何简化计算,减少计算时间和内存容量,并确保解具有足够的精确性.基于矩阵奇异值分解的特征正交方法(Proper Or*收稿日期:2018-10-25基金项目:国家自然科学基金项目资助(11461013)作者简介:张国平(1994-),女,贵州遵义人•硕士研究生,研究方向:计算数学E-mail:zygpzhang®92经济数学第36卷thogonal Decomposition)能提供具有足够高精度而自由度又较小的低阶模型,简化计算,节省CPU和内存.文中所介绍的特征正交分解方法旳主要是提供一种有效逼近大量数据的最优逼近方法,它的实质是在最小二乘意义下⑷找寻能代表已知数据的一组正交基.即一种求已知数据的最优逼近方法.此外,由于POD方法是在最小二乘意义下最优的,所以该方法有完全依赖数据而不对数据作任何先验假设的优点.在文献[7]中以对流-扩散-反应过程为例,设计了基于低阶模型的线性二次调节器的最优控制⑺,将离散空间模型的阶数大大地降低了,其仿真实现了最优反馈控制的实时应用,但是没有对二维对流扩散方程描述的系统实现最优控制.本文将特征正交分解应用于二维非稳态对流扩散边界控制问题,在文献[7]的基础上将低阶模型与最优控制问题相结合提出了基于低阶模型的二维对流扩散边界控制问题.首先采用有限差分法计算出由瞬时对流扩散方程解集构成的瞬像(snapshots),再利用奇异值分解⑷和玖)D分解方法获得对流扩散瞬像的最优特征正交基,再与伽辽金投影方法结合将高阶的状态空间模型转化为精度较高的低阶模型,并结合线性二次调节器的最优控制方法,得出基于无约束的线性二次调节器的最优反馈控制的输入/输出.以二维对流扩散边界控制问题为例,结果表明在保证较高精度的优化结果的同时可大幅度提高求解速度.2对流扩散最优控制模型降阶的算法2.1最优控制问题描述以二维对流扩散边界控制问题为例,考虑如下初边值问题:dU.dU.dU rw’u./u帀+5+%矿D(狂+昕),工€[0,兀];y E E[0,1],y=0,17=u;y=兀,(7=0,(1)工=0,学=0或z=X,学=0,dJC djC、£=0,17=0.式中2=0,U=“是输入变量,石=0是输出变量,“,5是反应器中流动速度,D为扩散系数.在二维对流扩散方程条件下,目标函数丿有如下的最优控制问题描述minjU<1>[y(t)—力了dt+(2)e2J[u(t)—U/J2dt.其中J为最优控制的目标函数,力和吋分别为控制过程输出和输入的稳态值,e为过渡过程中控制动作的权重.2.2对流扩散方程初边值问题的差分格式为探讨其差分格式,将区间[0,k]等分为j等分,每一等分的长度为h,时间步长用r表示.网格点为(心,y,t”),召=ih,y,=jh,t…=nr,i,j= 1,2,,m-j-1,n=1,2,"'Nth=7t/m.考虑最优控制问题(1)在"+1时刻的值,时间导数用向后差分格式,对流项采用迎风格式,扩散项采用中心差分格式.对式(1)离散整理得U旷=A0U;+A i S h“+AQ?.屮++A4,(3)式中:A。
第五章对流扩散问题(假扩散)
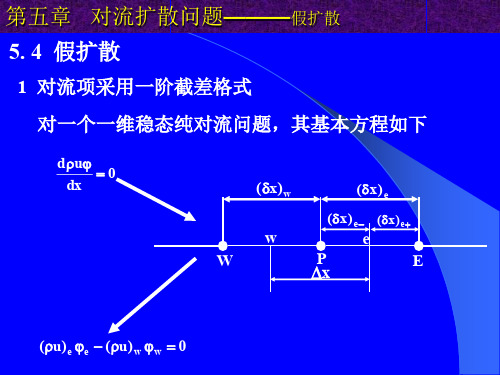
该问题的数值解如下:
1 n i
u t n u t n (1 ) i i 1 x x
MUD : du d ux d (( ) ) dx dx 2 dx
第五章 对流扩散问题———假扩散
由图可以看出,在区间 P 2 ,中心差分格式预报的 P 值优于迎风格式的预报值。对比这两种格式,其扩散项 的处理是完全相同的,所不同的仅仅是对流项的处理上 ,在中心差分格式中对流项的差分格式具有二阶精度, 而在迎风格式中对流项的差分格式只具有一阶精度。在 区间 P 2 ,两种格式预报 P值所表现出的差异性恰恰是 这两种格式精度不同的体现。观察上图,迎风格式所预 报的 P值具有该高不高和该低不低的特点,这一特点正 是由一阶精度迎风格式所引起的扩散系数为 ux / 2 的 假扩散项造成的。也反映了假扩散项的影响。
n n ux ut 2 n ( ) i u( ) i (1 )( 2 ) i O( x 2 , t 2 ) t x 2 x x
由此可以看出,我们前边得到的差分方程所逼近的是 一个非稳态对流扩散问题,而非原型问题所要求的非 稳态对流问题。
第五章 对流扩散问题———假扩散
1 n (1 P
ut n ut n ) P W x x
用编号法表示
1 n i
1 n , n 在点 (i, n) i i 1
u t n u t n (1 ) i i 1 x x
做Taylor展开
n n u 2 n 1 2 n ( ) i u( ) i ( 2 ) i x ( 2 ) i t O( x 2 , t 2 ) t x 2 x 2! t
第五章 对流扩散问题———假扩散
将 i 1 和 i 1 台劳 级数展开代入
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最终表达式
a P P a E E a W W a N N a S S b
a E D e A ( P e ) D e A P e F e,0
a W D w B ( P w ) D w A P w F w ,0 a N D n A ( P n ) D n A P n F n ,0
P WBiblioteka PWS 2对策• 尽量减小流线与网格线间的倾斜和交叉。采用自 适应网格,如“旋转坐标”技术。
• 改进对流项格式设计方案,采用高阶精度迎风格式
• 对一阶精度迎风格式加入适量的逆耗散,以减小 扩散系数
• 离散格式中包含更多邻节点个数
5.4.3 非常数源项引起的 虚假扩散
这是一种特殊情况,但在许 多计算热物理问题中出现
修正的偏微分方程(MPDE)
• 一维对流方程(波动方程)
uau0 (a0) t x
• 一阶迎风格式 u n j 1 u n j c ( u n j u n j 1 ) ( c a t x )
修正的偏微分方程(MPDE)
• 迎风格式的泰勒展开
u t a u x 2 tu tt a 2 x u x x 6 t2u ttt a 6 x 2u x x x
• 流向扩散(streamwise diffusion): 只要求解 函数顺流向存在不为零的一阶导数时,它 使方程的真解被光滑,导致数值计算误差
5.4.2 网格取向效应引起的 交叉扩散
由于网格线和流线之间并非平行或垂直 ,而是有一定角度的交叉而导致的扩散
虚假扩散逐渐抹平阶梯分布
0
0
来流与网格线平行和交叉时 迎风格式计算结果
• 系数表达式见课本
5.3.3 多维对流扩散问题的 边界条件处理
几种可能的边界条件
• 以有回流的突扩通道为例
入口边界
• 一般规定入口边界上的函数值 和
流速 u 和 v 的分布
对称边界
• 由对称性,有
v0, u0, 0
y y
固壁边界
• 对粘性流体,壁面无渗透,其壁面速度为 零,即 uv0
• 对于 ,可提1、2、3类边界条件。
积分结果
() P t() 0 P x y ( J e J w ) ( J n J s ) ( S C S P P ) x y
• 连续方程积分结果
P t P 0 x y(F eF w )(F nF s)0
两式相减合并
P 0 ( P tP 0 ) x y (J e F eP ) (J w F wP ) (J n F nP ) (J s F sP ) (S C S PP ) x y
多维非稳态对流扩散问题分析
5.3.1 二维非稳态对流扩散 方程的离散
1.直角坐标系下的对流扩散 方程和连续方程
• 控制方程
( t) ( x u ) ( y v ) x x y y S
• 连续方程
(u)(v)0
t x y
引入通量密度
• 对流扩散总通量密度:
• MPDE
自循环消元过程
u t a u x a 2 x ( 1 c )u x x a 6 x 2 (2 c 1 )(c 1 )u x x x
虚假的流向扩散
• MPDE中的二阶空间导数代表扩散作用(粘 性效应),相当在原始方程中增加了扩散作 用(人工粘性作用),这引入了原始方程中没 有的一种虚假扩散。
考虑非常数源项时的数值结果
评述
• 这种虚假扩散现象是一种特殊情况,但可 能在不同的离散格式、不同源项分布情况 下出现。
• 如何减少这种虚假扩散,还有待深入研究 ,但对流项采用高阶精度离散格式,对减 轻相应的影响显然是有益的
a S D s B ( P s ) D s A P s F s,0
• 根据采用的三点离散格式不同,选定A(|P|) 函数形式不同,参见前一节的表格
5.3.2 三维非稳态对流扩散方程
• 离散结果
a P P a E E a W W a N N a S S a T T a B B b
• 对流、扩散通量项:时间积分取隐式,空 间取均匀分布
tt t
n s
w eJxxdxdydtJxeJxwyt(JeJw)t
tt t
n s
w eJyydxdydtJy
nJy
sxt(JnJs)t
源项
• 线化为
SSCSP (SP0)
• 时间、空间均取均匀分布
net t
s wt S d td x d y (S C S P) x y t
Jxu x, Jyv y
• 质量通量密度:
Fxu, Fyv
用通量表示的控制方程
• 控制方程:
()Jx Jy S
t x y
• 连续方程
()Fx Fy 0
t x y
2.控制容积积分离散
• 非稳态项:假设沿空间为均匀分布
s nw ett t ( t)d td x d y ( )P ( )0 P x y
出口边界
• 难点:除非实测,不可能获得出口截面信息
• 出口截面局部坐标单向化:假定出口截面节 点对它近邻的内节点无影响,从而令边界节 点对内节点的影响系数为零
5.4 对流扩散方程离散格式的 虚假扩散问题
1. 人工粘性引起流向扩散 2. 网格取向引起交叉扩散 3. 非常数源项带来的虚假扩散
5.4.1人工粘性所引起的 流向扩散
