多污染源对流_扩散方程的参数识别反问题
基于机器学习的对流扩散参数识别方法

基于机器学习的对流扩散参数识别方法基于机器学习的对流扩散参数识别方法一、引言对流扩散现象在许多科学和工程领域中都具有重要意义,例如环境科学中的污染物扩散、流体力学中的热传递和物质传输等。
准确识别对流扩散参数对于理解和预测这些过程至关重要。
传统的参数识别方法往往依赖于复杂的数学模型和大量的实验数据,并且在处理复杂的实际问题时可能存在局限性。
机器学习作为一种强大的数据分析工具,为对流扩散参数识别提供了新的思路和方法。
二、对流扩散基本原理1. 对流扩散方程对流扩散过程通常可以用对流扩散方程来描述。
对于一维情况,对流扩散方程可以表示为:∂C/∂t + u∂C/∂x = D∂²C/∂x²其中,C是浓度,t是时间,x是空间坐标,u是对流速度,D是扩散系数。
这个方程描述了物质在对流和扩散作用下的浓度变化。
2. 对流扩散的物理意义对流是指物质随着流体的整体流动而发生的迁移,它与流体的速度有关。
扩散则是由于分子的热运动而导致的物质从高浓度区域向低浓度区域的迁移。
在实际情况中,对流和扩散往往同时存在,并且相互作用。
三、传统对流扩散参数识别方法1. 解析方法解析方法是通过求解对流扩散方程的解析解来确定参数。
对于一些简单的几何形状和边界条件,可以得到对流扩散方程的解析解。
然而,这种方法的应用范围非常有限,因为大多数实际问题都具有复杂的几何形状和边界条件。
2. 数值方法数值方法是通过将对流扩散方程离散化,然后利用计算机求解离散化后的方程来确定参数。
数值方法可以处理复杂的几何形状和边界条件,但是它需要大量的计算资源和时间,并且对于一些非线性问题可能存在数值不稳定的问题。
3. 实验方法实验方法是通过进行实验来测量对流扩散过程中的相关参数。
实验方法可以直接获取实际数据,但是它需要昂贵的实验设备和大量的实验时间,并且实验结果可能受到实验误差的影响。
四、机器学习在对流扩散参数识别中的应用1. 机器学习基本概念机器学习是一种通过数据学习模式和规律的方法。
【国家自然科学基金】_污染源识别_基金支持热词逐年推荐_【万方软件创新助手】_20140802
2012年 序号 1 2 3 4 5 6
科研热词 推荐指数 飞行时间-二次离子质谱 1 表面分析 1 应用进展 1 大气科学 1 大气气溶胶 1 单颗粒分析 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
科研热词 污染源识别 非点源污染 长乐江流域 资料不足 空间变异 生物化学降解 源识别 污染场地 氮素 梯度法 最优化 地统计学 地下油罐泄漏 地下水 土壤重金属 供水管网 arcswat
推荐指数 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
2014年 科研热词 高速铁路箱梁 风险系统 频谱分析 结构局部振动 结构噪声 空间邻近 相干分析 环境背景值 环境暴露 环境基线 水污染 氨氮 奎河 噪声源识别 pm2.5 gis 推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Hale Waihona Puke 2010年 序号科研热词 1 重金属 2 多环芳烃 3 可吸入颗粒物
推荐指数 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
2011年 科研热词 污染源 贵阳市 方法对比 大气气态总汞 重金属 硝酸盐 活性污泥 河流排放通量 污水处理厂 氮同位素 氧同位素 有效态 地下水 土壤 全氟辛酸 全氟辛烷磺酸 推荐指数 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1
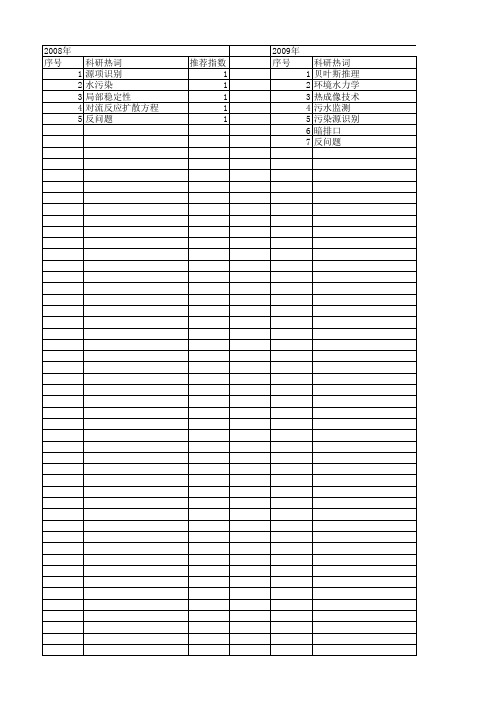
2008年 序号 1 2 3 4 5
科研热词 源项识别 水污染 局部稳定性 对流反应扩散方程 反问题
推荐指数 1 1 1 1 1
一类对流-扩散方程源项反问题的数值解法

同伦摄 动方 法[ 有别 于传统 的摄 动方 法 , 1 它不依 赖小参 数 , 而是应 用 同伦技 术 , 造 一个 含嵌 入参 数 p 构
∈[ ,] 0 1 的方 程 , 然后把 嵌人参 数作 为小参 数. 这种方 法 既克服 了传统 摄 动理论 的不 足 , 充分应 用 了各 种摄 又 动方法 . 文献 EJ 用 同伦摄 动方法 求解 了 B r es 程 和 Kotwe —eVr s方 程 的解 ;文献 E J利用 同 3利 ugr 方 re gd i e 4 伦摄动方 法分 别求解 了一类 非齐 次抛 物型偏 微分 方程 和一类 非线 性偏 微 分方 程 的解 ;文献 E 3利用 同伦 摄 s
f x,) 问题 称 为源项 识别 问题. ( 的
反演 f x,) 往要增 加其 他 附加 条件 , ( £往 比如通过 终值 条件 “( , )或 边界上 的观 测值 “( ,) 柏来 z T ,z £ l
反演 f x,) 一般来 说 , 定 f x,)的反问题 是非 线性 的 , 文采用 的附加 条件 为 终值 条件 ( , ) 对实 ( . 决 ( 本 zT.
Vo . 9 NO 6 13 .
NO V. 2 0 01
一
类对 流 一扩 散 方程 源项 反 问题 的数 值 解 法
阮周 生 ,王 泽 文 ,何 杰
( 华理 工 大 学 数 学与 信 息科 学 学 院 , 西 抚 州 34 0 ) 东 江 4 0 0
摘
要 : 用 函数 逼 近 与 同伦 摄 动 方 法 , 一 类 对 流 一 扩 散 方 程 源 项 识 别 问 题 转 化 为 分 布 参 数 系 统 的 最 优 利 将
基于遗传算法的对流扩散方程逆时反问题的数值求解

关键 词 :正 则化 ;积 分 方程 ;逆 时反 问题 ;遗 传 算 法 ;对 流扩散 方程 摘 要 :利 用 Tk oo i n v正 则化 方 法解 第 一类 Feh l 积分 方 程 获得 该逆 时反 问题 的 解 ,并 h rd om
但 是如果 对极 小化 加上进 一 步的 限制 ( 如是 最 小模解 ) ・ 例 ,则 可保 证极 小元 的存在 唯 一性 。 一 的角度 ) ,或 者使得 极小 元满 足 的方程 是 一个第 二 类 的方 法 ( 积分 方程 理 论 的 角 度 ) 从 。这 就 是 Tk oo i nv h 正 则化 方法解 不适 定 问题 的基本方 法 。具体说 来 ,该 问题 提 为 :对 有界线性 算 子 :_一l和 Y ,求 Y , 一 ∈T
展 的正则 化方 法 。
本文在 Tkoo 正则化原理的基础上 ,结合遗传算法 的优点,提出了应用遗传算 法代替一般的优化 i nv h
方法来 处理 泛 函 ,以便使 问题 的解决 更加 有效 ,更 使求 出 的解具 有稳定性 好 、精度 高 的特点 。
1 Tk o o 则 化 方 法 的原 理 ih n v正
第3 0卷
2 遗传 算 法 和 正 则 化方 法 的结合
遗传算 法 ( e e cAgrh G n t l i m,G i ot A) 是 由美 国 Mc ia i gn大学 } l n h l l d教 授 和他 的学 生 发 展 建 立 的 , oa 其思 想起 源于生 物学适 应 者生存 的 自然选择 规律 ,是 一 种新兴 的 自适 应随机 搜索 疗法 ,它对 优化 对象既 不 要求 连续性 也不要 求 可微 ,并 具有 极强 的鲁 棒性 和 内在并行 计算 机制 。对 于任 何 复杂 的 问题 ,只要定 义 了 搜索 空间 ,而不需 定 理初值 。并对 整个搜索 区间 ,不是 使用某 一个数 据 ,而 是使 用 一组数据 。 且对 数据进
一类对流-扩散方程热源识别反问题

摘要 : 根据 测量 数据 , 利用分 离变量法, 得到未知源 函数和测量数据 之间 的关 系式. 类问题称为未知 源识别反 问 这 题, 是典 型的不适定 问题. 利用截 断正则化方 法, 得到 问题 的一个 正测 近似 解, 并且 给 出正则解和精 确解之 间具 有
Hoe l r型的误差估计. 关键词 :热源;反 问题 ; 对流一 扩散方程 ;截断方法 中图分类号 : 7. 6 O15 2 文献标识码 : A
一
类对 流一 扩散方程热源识别反问题
李晓晓 ,郭亨贞 ,万诗敏。 ,汪训 洋 杨 帆 ,
7 05 ; .兰州城市学 院 教育学院 , 30 0 2 甘肃 兰州 707 ; . 3 0 0 3 天津城市建设学院 基础学科 部, 天津
( .兰州理工大学 理学院 , 1 甘肃 兰州
308 0 3 4)
LIXio xa a - io ,GUO n - h n ,W AN h- n ,W ANG n y n He g z e S i mi 。 Xu - a g ,YANG a F n
( .S h o in e,L n h v o c .,l z o 7 0 5 1 c o l Sc c of e a z ouUni. fTe h mn h u 3 0 0,Chn ia;2 I siue o u a in,La z ouCi nv riy,La z o . n tt t fEd c to n h t U iest y ah u
u e aa wa b an d b sn a ib es p r to eh d Th sp o lm sc le h n e s r be rd d t so ti e yu ig v r l e a a in m t o . a i r b e wa ald t ei v rep o lm o d n ic t n o n n wn s u c n sa t pc li— o e r b e . A e ua ie p r x ma es l — fie t ia i fu k o o re a d wa y ia l p sd p o lm f o l r g lrz d a p o i t ou t n o h n es r b e wa b an d b sn r n ae e ua ia in me h d a d t ee tm ain o i ft eiv r ep o lm so t ie y u ig tu c t d r g lrz t t o n h si to f o o Ho e-y ee r ro e u aie o u in fo x c n sgv n,lo lrt p ro fr g lrz d s lto r m e a to ewa ie as . Ke r s h a o r e n e s r b e ;c n e to - i u in e u t n r n ain me h d y wo d : e ts u c ;iv r ep o lm o v cin df so q a i ;tu c to t o f o .
一个二维多点源扩散方程的源强识别反问题

龙源期刊网 一个二维多点源扩散方程的源强识别反问题作者:殷凤兰来源:《读写算》2013年第38期摘要:对于一类带有多个点源的二维扩散方程问题,应用有限差分法给出了一个数值求解格式,并在已知点源个数及其位置的前提下,应用最佳摄动量正则化算法对源强进行了数值反演,并讨论了正则参数的不同选取对反演算法的影响。
关键词:扩散方程;多点源;反问题;最佳摄动量正则化算法引言分布式参数系统模型对精确描述和有效控制许多物理和工程问题起着关键作用.近几十年来,分布式参数系统识别的反问题研究受到人们越来越多的关注,特别是关于源项的估计或识别(寻源反问题)研究在环境科学与工业应用等领域显得尤为重要.例如,在环境水利学领域,如何寻找河流、湖泊和城市水环境的污染源,以及在微波加热过程、化学反应过程和工业设计与制造领域,探测未知的发热源等问题都是数理方程反问题研究的重点.由于广阔的实际应用背景,以及反问题自身的不适定性,抛物型方程点源反问题更是研究的热点和难点。
对于抛物型方程的点源识别反问题,由于含有Dirac广义函数,处理起来不像一般连续源强反问题那么容易.对此,国内外不少学者也做了大量工作,如文献通过上述数据可以看出正则参数的不同取值对反演结果有一定的影响,在本例中正则参数μ取值越小迭代次数越少,而且误差就越小;数值微分步长的不同选取对反演结果的影响不大,在合理取值情况下,此算法还是比较有效的。
参考文献[1]El Badia A,Ha-Duong T,Hamdi A.Identification of a point source in a linear advection -dispersion-reaction:application to a pollution source problem [J].Inverse Problems[2]Hamdi A.Identification of a time-varying point source in a system of two coupled linear diffusion-advection-reaction equations:application to surface water pollution [J].Inverse Problems,[3]Leevan Ling,Masahiro Yamamoto,Y.C.Hon,et al.Identification of source locations in two-dimensi- noal heat equations[J].Inverse Problems[4]陆金甫,关治.偏微分方程数值解法[M].北京:清华大学出版社[5]苏超伟.偏微分方程逆问题的数值解法及其应用[M].西安:西北工业大学出版社。
对流扩散方程解析解

对流扩散方程解析解对流扩散方程(Convection-DiffusionEquation)是在求解流体,如气体或液体的输运问题时需要使用的普通微分方程。
它表示物质被三种因素作用所引起的质量流动:对流、扩散和反应。
在本文中,我们将讨论对流扩散方程的解析解,以及它在工程中的重要作用。
首先,要理解对流扩散方程,我们必须从它的数学形式开始。
它可以用以下形式表示:$$frac{partial c}{partial t}+ vec{u} cdotabla c-Dabla^2 c=R$$在这里,$c$表示物质的浓度,$vec{u}$表示流体的速度,$D$表示物质的扩散系数,$R$表示反应的密度。
对流扩散方程的解析解是一种运用数学方法来求解这个方程的方法。
它主要是利用积分变换法(Integral Transform Method),将复杂的运动学问题转化为一组常微分方程求解。
解析解方法在解决一定类型的常微分方程时尤其有用,特别是当一个系统的边界条件是确定的时。
解析解的优势在于它可以提供直观的解,方便比较和评估结果,便于理解物理机理。
它也可以提供准确的结果,并可以用于组合的求解方法中。
在工程领域,对流扩散方程解析解的应用非常重要。
它可以被应用于温度或物质浓度输运,以及其他类似现象的计算。
例如,对流扩散方程可以用来模拟一定范围内扩散方式的热量传输,从而推测温度场分布;也可以用来模拟入口流场和出口的物质浓度的变化;它还可以用来描述各种物质在工程系统内的扩散问题。
再者,解析解方法也被广泛应用于制药行业。
对流扩散方程可以用来模拟药物在体内的运动,从而计算出最佳控制方案,以达到药物最佳疗效。
这不仅可以为药物分布模型提供依据,还可以用来估算药物组分以及药物与体细胞的相互作用等工程相关问题,从而帮助制药公司最大程度地提高药品安全性和疗效。
最后,对流扩散方程的解析解是一种非常有效的数学方法,它可以帮助我们更加清晰地理解流体输运问题,并可以提供准确可靠的结果。
《对流扩散方程》课件

环境科学
描述污染物在大气、水体等环境 介质中的扩散、输移和归宿。
在环境科学中,对流扩散方程用 于模拟污染物在大气、水体等环 境介质中的扩散、输移和归宿过
程。
在环境保护、污染治理等领域, 对流扩散方程具有重要的应用价
值。
化学反应动力学
描述化学反应在流体或固定床 反应器中的传递和反应过程。
在化学反应动力学中,对流 扩散方程用于模拟化学反应 在流体或固定床反应器中的
初始条件
指定在求解开始时刻的解的性质,如 常数、函数等。
03 对流扩散方程的应用
流体动力学
01
描述流体在运动状态下的物质传递和扩散现象。
02
在流体动力学中,对流扩散方程用于模拟流体中的物质传递过
程,如温度、浓度、速度等。
在航空航天、船舶、汽车等领域的流体动力学分析中,对流扩
03
散方程被广泛应用。
应用于多尺度问题
研究对流扩散方程在多尺度问题中的应用,如 微纳尺度流动、大气污染扩散等。
探索新的应用领域
将该方程应用于其他领域,如生物医学、环境科学等。
与其他领域的交叉研究
与流体动力学结合
研究对流扩散方程与流体动力学之间的相互 作用和影响,探索更深入的物理机制。
与偏微分方程理论的交叉
将对流扩散方程的研究与偏微分方程理论相 结合,推动数学理论的发展。
02
03
有限体积法
将连续的求解域离散化为有限个小的 体积,在每个体积上近似函数,将微 分方程转化为代方程进行求解。
有限差分法
向前差分法
将微分方程中的导数项用前一步的函数值近似代替,得到向前差 分方程。
向后差分法
将微分方程中的导数项用后一步的函数值近似代替,得到向后差 分方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
