理论力学 静力学部分习题课
静力学习题课

3-6:对空间任意两个力,一定能找到一根轴,使这两个力在该轴上
的投影分别为零,对否?
正确
精品资料
静力学习题课
3-7:空间任意(rènyì)力系向两个不同的点简化,试问下述情况是 否可能。
(1)主矢相等(xiāngděng) 可能 (,2主)矩主相矢等不(相xiā等n,g主dě矩n相g)等。。 不可能
力2-2偶:吗平?面力偶系向作用面内任一点简化的结果可能是什么?
一个力偶或平衡
2-3:平面任意力系向作用面内任一点简化的结果可能是什么?
一个力、一个力偶、一个力和一个力偶、平衡
2-4:平面平行力系向作用面内任一点简化的结果可能是什么?
一个力、一个力偶、一个力和一个力偶、平衡 2-5:平面任意力系向作用面内任一点简化,一般情况下,主矢和 主矩是否与简化中心的选择有关?
下述三种情况下,物块B、C将发生怎样的运动
?
A.F1<F<F2
B. F2<F<F1 C. F<F2<F1
B和C一起运动 C运动、B不动
B、C均不运动
精品资料
mg θ
F
C
B
A
D.对于任意平面平行力系,一定存在某平面汇交力系与之等效。 错 E.对于任意平面汇交力系,一定存在某平面平行力系与之等效。 对
F.对于任意平面汇交力系,一定存在某平面力偶系与之等效。 错
2-10:图示平面结构,AB//CD,各构件自重不计
F
,在刚体上作用一力偶,试判断下述说法的正误:
M
E
A.这是平面力偶系问题,因为平面力偶系只
的关C系为_______。
M
A θ
P θB
A.FNA=FNB
清华大学版理论力学课后习题答案大全_____第3章静力学平衡问题习题解
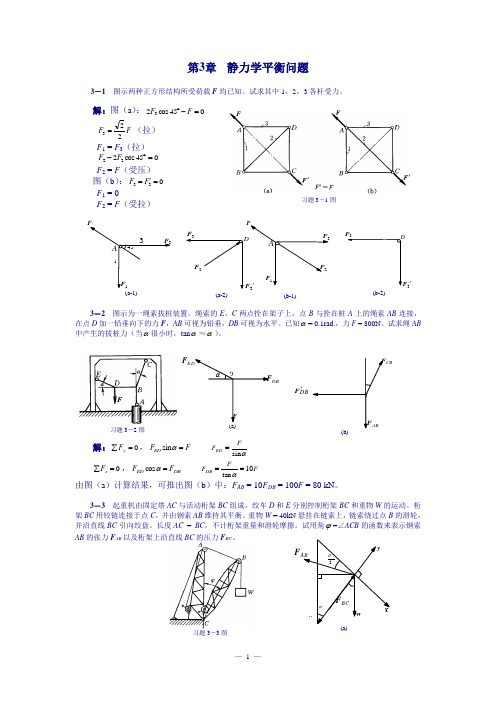
F DBCBDBF '习题3-3图第3章 静力学平衡问题3-1 图示两种正方形结构所受荷载F 均已知。
试求其中1,2,3各杆受力。
解:图(a ):045cos 23=-︒F FF F 223=(拉) F 1 = F 3(拉) 045cos 232=︒-F F F 2 = F (受压) 图(b ):033='=F F F 1 = 0F 2 = F (受拉)3-2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上,点B 与拴在桩A 上的绳索AB 连接,在点D 加一铅垂向下的力F ,AB 可视为铅垂,DB 可视为水平。
已知α= 0.1rad.,力F = 800N 。
试求绳AB 中产生的拔桩力(当α很小时,tan α≈α)。
解:0=∑y F ,F F ED =αsin αs i nFF ED = 0=∑x F ,DB ED F F =αcos F FF DB 10tan ==α由图(a )计算结果,可推出图(b )中:F AB = 10F DB = 100F = 80 kN 。
3-3 起重机由固定塔AC 与活动桁架BC 组成,绞车D 和E 分别控制桁架BC 和重物W 的运动。
桁架BC 用铰链连接于点C ,并由钢索AB 维持其平衡。
重物W = 40kN 悬挂在链索上,链索绕过点B 的滑轮,并沿直线BC 引向绞盘。
长度AC = BC ,不计桁架重量和滑轮摩擦。
试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。
(b-1)习题3-1图(a-1)(a-2)'3(b-2)习题3-2图F习题3-5图习题3-4图 解:图(a ):0=∑x F ,0sin 2cos=-ϕϕW F AB ,2sin2ϕW F AB =0=∑y F ,02sincos =---ϕϕAB BC F W W F即 2s i n 2c o s 2ϕϕW W W F BC ++=W W W W 2)c o s 1(c o s =-++=ϕϕ3-4 杆AB 及其两端滚子的整体重心在G 点,滚子搁置在倾斜的光滑刚性平面上,如图所示。
《理论力学》静力学典型习题+答案
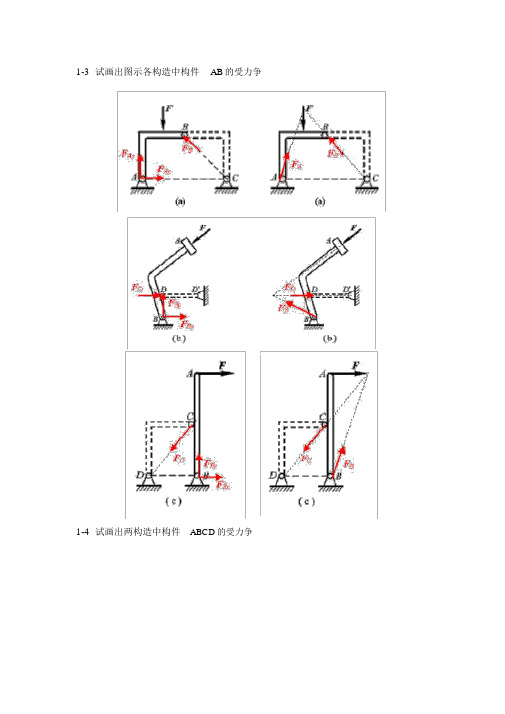
1-3 试画出图示各构造中构件AB的受力争1-4 试画出两构造中构件ABCD的受力争1-5 试画出图 a 和 b 所示刚系统整体各个构件的受力争1-5a1-5b1- 8 在四连杆机构的ABCD的铰链 B 和 C上分别作用有力F1和 F2,机构在图示位置均衡。
试求二力F1和 F2之间的关系。
解:杆 AB,BC, CD为二力杆,受力方向分别沿着各杆端点连线的方向。
解法 1( 分析法 )假定各杆受压,分别选用销钉 B 和 C 为研究对象,受力以下图:yyFBCC xB Fo45BCx30o o F60F2CDF AB F1由共点力系均衡方程,对 B 点有:F x0F2F BC cos4500对 C点有:F x0FBC F1 cos3000解以上二个方程可得:F12 6F2 1.63F23解法 2( 几何法 )分别选用销钉 B 和 C 为研究对象,依据汇交力系均衡条件,作用在 B 和C 点上的力构成关闭的力多边形,以下图。
F F2BCF AB o30o45CD60oFF BC F1对 B 点由几何关系可知:F2F BC cos450对 C 点由几何关系可知:F BC F1 cos300解以上两式可得:F1 1.63F22-3 在图示构造中,二曲杆重不计,曲杆AB 上作用有主动力偶 M。
试求 A 和 C 点处的拘束力。
解: BC为二力杆 ( 受力以下图 ) ,故曲杆 AB 在 B 点处遇到拘束力的方向沿BC 两点连线的方向。
曲杆AB遇到主动力偶M的作用, A 点和 B 点处的拘束力一定构成一个力偶才能使曲杆AB保持均衡。
AB受力以下图,由力偶系作用下刚体的均衡方程有(设力偶逆时针为正):M0 F A10a sin(450 )M 0F A0.354Ma此中:tan 1。
对 BC杆有:F C FB F A0.354M 3aA,C两点拘束力的方向以下图。
2-4解:机构中 AB杆为二力杆,点A,B 出的拘束力方向即可确立。
理论力学 静力学 习题答案
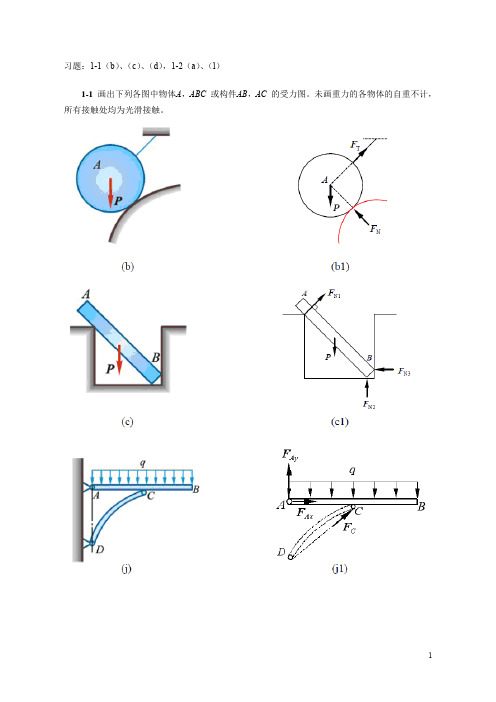
F
解得
y
0 , FAy FB1 y 0
FAy F qa
A
M
解得
3 0 , M A q a a FB1 y a FB1x 3a 0 2 M A ( F qa ) / a
10
2-47 平 面 构 架 的 尺 寸 及 支 座 如 图 所 示 , 三 角 形 分 布 荷 载 的 最 大 集 度 q0 2kN/m ,
2
3
习题:2-3,2-5,2-6,2-8,2-12,2-14,2-18,2-10,2-40 2-3 如图示刚架的点B 作用一水平力F,刚架重量略去不计。求支座A,D 的约束力FA和FD。
解: 一、取刚架为研究对象,画受力图,如图(b)。 二、列平衡方程,求支座 A,D 的约束力 FA 和 FD。 由三力平衡汇交定理,支座A 的约束力FA 必通过点C,方向如图(b) 所示。取坐标系Cxy , 由平衡理论得
0.1m的滑轮。有一跨过滑轮的绳子,其一端水平系于墙上,另一端悬挂有重为P =1800 N的重物。
如AD = 0.2m,BD = 0.4m,ϕ = 45°,且不计梁、杆、滑轮和绳的重力。求铰链 A 和杆BC 对 梁的约束力。 解: 一、研究对象:整体,坐标及受力如图b所示 二、列方程,求铰链 A 和杆BC对梁的约束力
FsA f s FNA FsB f s FNB
联立以上5式,得
s 0.456l
4-10 均质箱体 A 的宽度 b = 1 m,高 h = 2 m,重力 P = 200 kN,放在倾角 θ = 20° 的斜面 上。 箱体与斜面之间的摩擦因数 fs =0.2 。 今在箱体的 C 点系一无重软绳, 方向如图所示, 绳的另一端绕过滑轮 D 挂一重物 E。 已知 BC = a = 1.8 m。 求使箱体处于平衡状态的重物 E 的重量。 解: 一、物体E重量较小时,临界受力如图b,此时为 1、 临界下滑
《理论力学》静力学典型习题+答案00

1-3 试画出图示各结构中构件AB的受力图1-4 试画出两结构中构件ABCD的受力图1-5 试画出图a和b所示刚体系整体各个构件的受力图1-5a1-5b1- 8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示:由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):0=∑M 0)45sin(100=-+⋅⋅M a F A θ aM F A 354.0=其中:31tan =θ。
对BC 杆有:aM F F F A B C 354.0=== A ,C 两点约束力的方向如图所示。
2-4FF解:机构中AB杆为二力杆,点A,B出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件,点O,C处的约束力方向也可确定,各杆的受力如图所示。
习题课_静力学

解:研究对象: 起重机 分析力:
Gb
ea
满载时
P, W, G, NA , NB
AP B
W
mB(F) NAd PeWa G(b d) 0
NA d NB
不向右翻倒,有NA 0
Pe Wa G(b d )
NA
d
0
解不等式得
G Wa Pe 54kN bd
Gb
e
空载时 P, G, NA , NB 不向左翻倒
mo (F) m SABr sin[180 ( )] 0
XO
m
NB A
整体考虑
m
S AB r
sin(
)
Prsin( ) cos
O
SAB’
YO
X XO P 0 XO P Y YO N B 0 YO Ptg
p.16
例题
例题
例17. 图示连续梁,载荷和尺寸如图,各杆的自重不计,A端
NB
Tc
sin (h d ) Tc
2b
cosb
1.67kN
代入第二式解得 N A TC cos NB 2.19kN
或利用两矩式
mE (F) NA 2b Tc sin (h d) Tc cosb 0
p.12
例题
例题
例13. 已知:图示L形杆AOBC自重不计,O处挂一重物重为P,
X
80
p.8
例题
例题
例8. 重力坝受力情况如图,长度单位为m, AB = 5.7m, G1 =
450kN, G2 = 200kN, P1=300kN, P2 = 70kN, =16o40’。
求力系向A点简化的结果,以及力系的最终简化结果。
解:先求力系向A点简化的主矢
理论力学习题及解答1
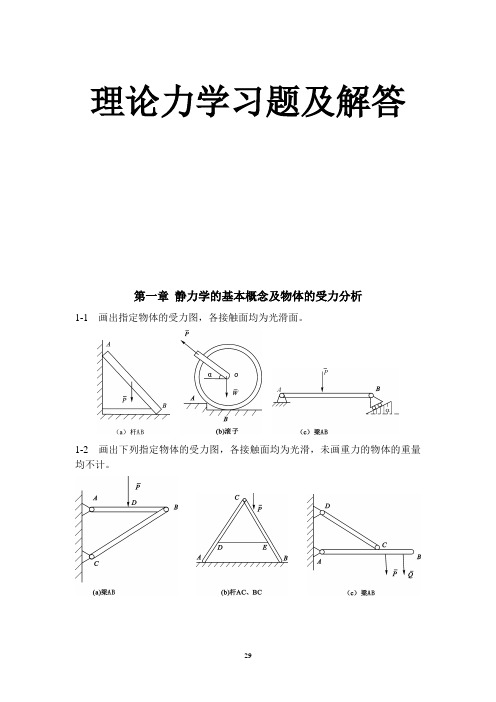
理论力学习题及解答第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图,各接触面均为光滑面。
1-2 画出下列指定物体的受力图,各接触面均为光滑,未画重力的物体的重量均不计。
1-3 画出下列各物体以及整体受力图,除注明者外,各物体自重不计,所有接触处均为光滑。
(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN,用绳子挂在支架的滑轮B上,绳子的另一端接在铰车D 上,如图所示。
转动铰车,物体便能升起,设滑轮的大小及滑轮转轴处的摩擦忽略不计,A、B、C三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB和支杆CB所受的力。
2-2 用一组绳悬挂重P=1kN的物体,求各绳的拉力。
2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN,P2=800kN及制动力T=193kN,桥墩自重W=5280kN,风力Q=140kN。
各力作用线位置如图所示,求将这些力向基底截面中心O简化的结果,如能简化为一合力,试求出合力作用线的位置。
2-4 水平梁的支承和载荷如图所示,试求出图中A、B处的约束反力。
2-5 在图示结构计算简图中,已知q=15kN/m,求A、B、C处的约束力。
2-6 图示平面结构,自重不计,由AB、BD、DFE三杆铰接组成,已知:P=50kN,M=40kN·m,q=20kN/m,L=2m,试求固定端A的反力。
图2-6 图2-72-7 求图示多跨静定梁的支座反力。
2-8 图示结构中各杆自重不计,D、E处为铰链,B、C为链杆约束,A为固定端,已知:q G=1kN/m,q=1kN/m,M=2kN·m,L1=3m,L2=2m,试求A、B、C 处约束反力。
图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成,O、B处为铰链,A、E是固定铰支座,尺寸如图,已知:r=20cm,在滑轮上吊有重Q=1000N的物体,杆及轮重均不计,试求支座A和E以及AO杆上的O处约束反力。
工程力学——静力学部分习题第一章静力学公理与物体的受

B P2
(a)
2
C P
A
B
(b)
3
第二章 平面汇交力系与平面力偶系
一、判断题
1. 两个力 F1、F2 在同一轴上的投影相等,则这两个力大小一定相等。 2. 两个力 F1、F2 大小相等,则它们在同一轴上的投影大小相同。 3. 力在某投影轴方向的分力总是与该力在该轴上的投影大小相同。
() () ()
F a bc
计算题
17.如图示圆形截面杆,已知各段面积分别为 A1 = 125m2 , A2 = 60m2 , A3 = 50m2 ,各段 长度分别为 l1 = 1m,l2 = 1.5m,l3 = 2m ,作用力 P1 = 4kN, P2 = 2kN, P3 = 0.5kN ,弹性模量 E = 200GPa 。1.作内力图;2.求杆的最大应力;3.求杆的最大伸长线应变。
应。
()
2.根据力的平移定理,可以将一个力分解成一个力和一个力偶,反之,共面内一个力
和一个力偶肯定能合成为一个力。
3.平面任意力系对其面内某点主矩为零,则该力系必可简化成一个合力。 ( )
4.平面任意力系向平面内某点简化得到的主矢一定就是该力系的合力。 ( )
5.平面任意力系向某点简化得一合力,则一定存在适当的简化中心使该力系简化成一
四、计算题 1. 图示四个平面共点力作用于物体的 O 点。已知 F1=F2=200KN, F3=300KN ,
F4=400KN 力 F1 水平向右。试分别用几何法或解析法求它们的合力的大小和方向。
F2
150o 45o
60o O
F1
F3
F 4
2. 梁 AB 的支座如图所示,在梁的中点作用一力 P=20KN,力与梁的轴线成 45o 角。如
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:AB 和BC 两杆为研究对象,受力及坐标如图所示。 由于未知力较多,尽可能用 轴矩式平衡方程(需保证方 程独立)求解,力求使取矩 轴与较多的未知力相交和平 行,从而使方程中所含未知 量最少。
1 MCz ' ' 0,( FN FAy) AC 0, FAy FN 2 ( P1 P 2)
MA 0 X 0
2X406 XD 152 0 XA XD 0 2 YA YD 0
XA XD 5.34( KN ),
Y 0
解得:
题4-46图
取DF为研究对象,画出受力图(题4-46图c)。列平衡方程。
MG 0 XD 152 YD( 203 203) 0 2 2
解:取曲杆为研究对象,受力及坐标如图 列平衡方程
Fx 0, F 0 Fy 0, F F 0 Fz 0, F F 0 Mx 0, M F c F My 0, F a M 0 Mz 0, M F a 0
静力学部分习课
3-20 无重曲杆ABCD 有2 个直角,且平面ABC 与平 面BCD 垂直。杆的D 端为球铰支座,A 端受轴承支 持,如图所示。在曲杆的AB,BC 和CD 上作用3 个 力偶,力偶所在平面分别垂直于AB,BC 和CD 三线 段。已知力偶矩 M2和 M3 ,求使曲杆处于平衡的力 偶矩M1和支座约束力。
9.若F=50kN,P=10kN, 墙与物体间的静摩擦因 数fs=0.3,则摩擦力为 10kN 。
10.平面系统受力偶矩为M=10kN的力偶作用,不计各 杆自重,则A支座反力的大小为为 5 kN。
11.一重为P,边长为a的 均质正方形薄板与另 一重为P/2的均质三角 形薄板焊接成一梯形 板,在A点悬挂。今欲 使底边BC保持水平, 3a 则边长L= 。
Dx Ay Dy Az Dz 1 Ay Az 2 3 Ay
Az
b 0
解得:
M2 M3 FAz , FAy a a M3 M2 FDx 0, FDy , FDz a a c b M1 M 3 M 2 a a
方法二
Fx 0, FDx 0 Fy 0, FAy FDy 0 Fz 0, FAz FDz 0 Mx 0, M 1 FDy c FDz b 0 My 0, FAz a M 2 0 Mz 0, M 3 FAy a 0
12.图示三铰刚架受力 F 作用,则A支座约束力的大小 为___________,B支座约 束力的大小为__________。
2 F 2
2 F 2
13.正三棱柱的底面为等腰三角形, 已知OA=OB=a,在平面ABED内有 沿对角线AE的一个力,图中,此 力对各坐标轴之矩 M (F ) 0 为: ; 2 M (F ) Fa 。 2
各方程联立求解
FCx 0
方法二
解:
受力如图列平衡方程
受力如图列平衡方程
1、空间任意力系的平衡方程为:
F 0 F 0 F 0 M
x y z
x
0
M
y
0
M
z
0
请问可否将后面的三个取矩轴改为另外三个直角坐标轴x’,y’和z’?
可以
2、空间平行力系的合成结果不可能为(D )
A.合力
B.合力偶
C.平衡
D.力螺旋
A
R’
F 3、图1所示一平面任意力系向O点简化后得到一个沿AB方向 O M B 的力和一个逆时针转向的力偶,则该力系最后合成的结果 图1 是( C ) A.作用于O点的一个力 B.一个合力偶 C.作用线在AB左侧的一个力 D.作用线在AB右侧的一个力
O
4、空间力对点之矩是( B ) A.代数量 B. 定位矢量 C.滑动矢量 D.以上答案都不对 5、下面关于力偶矩矢的说法错误的是( C ) A.矢量 C.定位矢量 B. 自由矢量 D.具有大小、指向和作用面方位三个要素
YD 1.33 KN), (
X 0
Y 0
XD NEC cos 0 YD NEC sin NBF sin 0
其中
cos
101.5
2 762 101.5
0.8
sin 1 0.82 0.6
解得:
NEC -4.45(KN), BF 2.23(KN) N
AC 1 MAy 0,FCz AC P 2 2 0, FCz 2 P 2 AC 1 MCy ' 0,( P1 FAz) AC P 2 2 0, FAz P1 2 P 2
Fx 0,F
Ax
FCx 0
(2)杆AB 为研究对象,受力及坐标如图所 示
x
y
结束
题2-46图 (a)所示结构AC、DF、BF及EC四杆组成,其中A、B、 C、D,E及F均为光滑铰链。各杆自重不计。试求支座A、D的 反力及杆BF、EC所受的力。
解:制定解题方案。整体约束反力行四个(XA、YA、XD、YD)。 取整体为研究对象虽然不能全部解出这四个未知量,但是 可以解出一部分。所以还是先取整体为研究对象,然后再 取AC或DF单体为研究对象。DF受力略比AC受力简单,取DF 为研究对象,列出的平衡方程项数将少些,计算相应地也 简单些,所以取DF为研究对象。具体解如下。 取整体为研究对象,画出受力图(题4-46图b)。列平衡方程
6.杆AB以铰链A及弯杆BC支持, 杆AB上作用一力偶,其力偶矩 大小为M,不计各杆自重,则 M A支座反力的大小为 a 。 7.正六面体三边长分别为 3 4,4,(单位m);沿AB连线 方向作用了一个力(单位 kN),其大小为F,则该力 对x轴的力矩为 2.4kN.m ; 对z轴的力矩为0。
2
8.图示系统只受作用而平衡。 欲使A支座约束力的作用线与 AB成30度角,则斜面的倾角 30 θ 应为 。
解得: M2 M3 FAz , FAy a a M3 M2 c b FDx 0, FDy , FDz ,M1 M 3 M 2 a a a a
3-21 2个均质杆AB 和BC 分别重P1 和P2,其端点A 和C 用球铰固定在水平面上,另1端B 由球铰链相连 接,靠在光滑的铅直墙上,墙面与AC 平行,如图 所 示。如AB与水平线交角为45°,∠BAC = 90°求A 和 C 的支座约束力以及墙上点B 所受的压力。
