基于MATLAB分析语音信号频域特征
基于Matlab的语音识别系统的设计本科毕业设计
摘要语音识别主要是让机器听懂人说的话，即在各种情况下，准确地识别出语音的内容，从而根据其信息执行人的各种意图。
语音识别技术既是国际竞争的一项重要技术，也是每一个国家经济发展不可缺少的重要技术支撑。
本文基于语音信号产生的数学模型，从时域、频域出发对语音信号进行分析，论述了语音识别的基本理论。
在此基础上讨论了语音识别的五种算法：动态时间伸缩算法(Dynamic Time Warping，DTW)、基于规则的人工智能方法、人工神经网络(Artificial Neural Network，ANN)方法、隐马尔可夫(Hidden Markov Model，HMM)方法、HMM和ANN的混合模型。
重点是从理论上研究隐马尔可夫(HMM)模型算法，对经典的HMM模型算法进行改进。
语音识别算法有多种实现方案，本文采取的方法是利用Matlab强大的数学运算能力，实现孤立语音信号的识别。
Matlab 是一款功能强大的数学软件，它附带大量的信号处理工具箱为信号分析研究，特别是文中主要探讨的声波分析研究带来极大便利。
本文应用隐马尔科夫模型(HMM) 为识别算法，采用MFCC(MEL频率倒谱系数)为主要语音特征参数，建立了一个汉语数字语音识别系统，其中包括语音信号的预处理、特征参数的提取、识别模板的训练、识别匹配算法；同时，提出利用Matlab图形用户界面开发环境设计语音识别系统界面，设计简单，使用方便，系统界面友好。
经过统计，识别效果明显达到了预期目标。
关键词：语音识别算法；HMM模型；Matlab；GUIABSTRACTSpeech Recognition is designed to allow machines to understand what people say,and accurately identify the contents of voice to execute the intent of people.Speech recognition technology is not only an important internationally competed technology,but also an indispensable foundational technology for the national economic development.Based on the mathematical model from the speech signal,this paper analyze audio signal from the time domain,frequency domain proceeding,and discussed the basic theory of speech recognition technology.Five algorithm are discussed:Dynamic Time Warping(DTW)、Rule-based Artificial Intelligence,Artificial Neural Network(ANN),Hidden Markov Model(HMM),HMM combined with ANN.The focus is put in the theoretical studies of Hidden Markov(HMM) model algorithm,and the classical HMM algorithm is improved.Speech recognition algorithm is realized in various programs,this article taking the method is to use Matlab powerful mathematical operation ability to realize the recognition of speech signal isolation. Matlab is a powerful mathematic software with a mass of toolboxes dealing with signal processing. It gives a terrific shortcut to the research of signal processing,especially the wave analysis. We can characterize the sound with key parameters such as intensity, frequency etc. In this paper, hidden Markov model (HMM) recognition algorithm using MFCC (MELfrequency cepstral coefficients) as the main voice characteristic parameters, the establishment of a Chinese digital speech recognition system, including the preprocessing of the speech signal,the extraction of characteristic parameters the training of the recognition template,identifying matching algorithm;the same time,the use of Matlab graphical user interface development environment designed speech recognition system interface,is designed to be simple,easy to use,friendly interface. Besides,to have a simple exploration of the voice recognition is another target.After statistics,recognition result obviously is made out as the expected goal.Key words：Speech recognition algorithm；HMM model；Matlab；GUI目录一、前言 (1)1.1语音识别的发展历史 (1)1.2语音识别研究现状 (1)1.3语音识别系统的分类 (2)1.4语音识别系统的基本构成 (3)1.5语音识别技术难点 (3)1.6语音识别发展前景 (4)二、语音信号分析 (4)2.1语音学知识 (4)2.1.1音素和音节 (5)2.1.2汉语的声调 (5)2.1.3语音信号产生模型 (6)2.2语音信号数字化和预处理 (7)2.2.1数字化 (7)2.2.2预加重处理 (7)2.2.3防混叠滤波 (8)2.2.4加窗处理 (8)2.3语音信号的时域分析 (9)2.3.1短时能量分析 (9)2.3.2短时平均过零率 (11)2.3.3短时自相关函数和短时平均幅度差函数 (12)2.3.4语音端点检测 (13)2.4语音信号的频域分析 (14)2.4.1滤波器组法 (14)2.4.2傅立叶频谱分析 (14)2.5特征参数提取 (15)2.5.1 LPCC倒谱系数 (15)2.5.2 Mel频率倒谱系数 (16)三、语音识别主要算法 (17)3.1动态时间伸缩算法 (17)3.2基于规则的人工智能方法 (18)3.3人工神经网络方法 (19)3.4隐马尔可夫方法 (20)3.5 HMM和ANN的混合模型 (21)四、隐含马尔可夫模型算法 (23)4.1 HMM的基本理论和数学描述 (23)4.2 HMM的三个基本问题及解决算法 (24)4.3 HMM算法的改进 (31)4.4 HMM的结构和类型 (33)4.5 HMM算法实现的问题 (34)五、基于Matlab环境下的语音识别算法实现 (35)5.1识别系统平台介绍 (35)5.2在Matlab中HMM算法的实现 (36)5.2.1端点检测 (36)5.2.2特征参数提取 (36)5.2.3训练和识别 (37)5.3实验结论分析 (38)六、结束语 (39)6.1回顾 (39)6.2展望 (39)七、致谢 (40)参考文献 (40)一、前言1.1语音识别的发展历史作为智能计算机研究的主导方向和人机语音通信的关键技术，语音识别技术一直受到各国科学界的广泛关注。
实验二基于MATLAB分析语音信号频域特征
实验二 基于MATLAB 分析语音信号频域特征一、实验目的信号的傅立叶表示在信号的分析与处理中起着重要的作用。
因为对于线性系统来说，可以很方便地确定其对正弦或复指数和的响应，所以傅立叶分析方法能完善地解决许多信号分析和处理问题。
另外，傅立叶表示使信号的某些特性变得更明显，因此，它能更深入地说明信号的各项物理现象。
由于语音信号是随着时间变化的，通常认为，语音是一个受准周期脉冲或随机噪声源激励的线性系统的输出。
输出频谱是声道系统频率响应与激励源频谱的乘积。
声道系统的频率响应及激励源都是随时间变化的，因此一般标准的傅立叶表示虽然适用于周期及平稳随机信号的表示，但不能直接用于语音信号。
由于语音信号可以认为在短时间内，近似不变，因而可以采用短时分析法。
本实验要求掌握傅里叶分析原理，会利用已学的知识，编写程序估计短时谱、倒谱，画出语谱图，并分析实验结果，在此基础上，借助频域分析方法所求得的参数分析语音信号的基音周期或共振峰。
二、实验原理1、短时傅立叶变换由于语音信号是短时平稳的随机信号，某一语音信号帧的短时傅立叶变换的定义为：()()()jwjwmn m X e x m w n m e∞-=-∞=-∑ （1.1）其中w(n-m)是实窗口函数序列，n 表示某一语音信号帧。
令n-m=k'，则得到(')'()(')(')jwjw n k n k X e w k x n k e∞--=-∞=-∑ （1.2）于是可以得到()()()jw jwnjwkn k X e ew k x n k e∞-=-∞=-∑ （1.3）假定()()()jwjwkn k X e w k x n k e∞=-∞=-∑ （1.4）则可以得到()()jw jwn jw n n X e e X e -= （1.5）同样，不同的窗口函数，将得到不同的傅立叶变换式的结果。
由上式可见，短时傅立叶变换有两个变量：n 和ω，所以它既是时序n 的离散函数，又是角频率ω的连续函数。
语音信号的频域分析
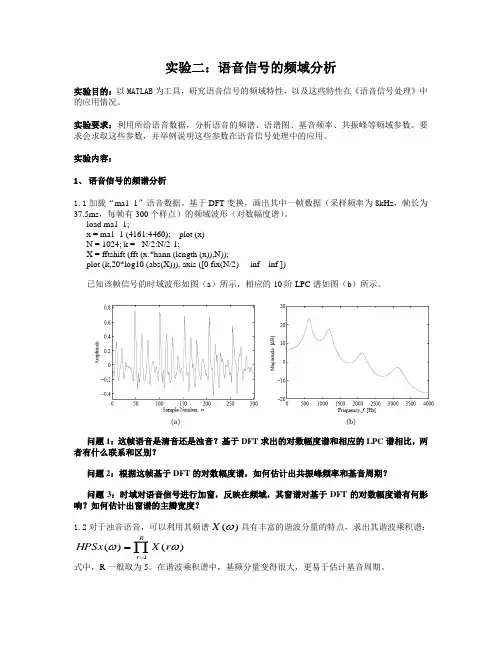
实验二：语音信号的频域分析实验目的：以MATLAB 为工具，研究语音信号的频域特性，以及这些特性在《语音信号处理》中的应用情况。
实验要求：利用所给语音数据，分析语音的频谱、语谱图、基音频率、共振峰等频域参数。
要求会求取这些参数，并举例说明这些参数在语音信号处理中的应用。
实验内容：1、 语音信号的频谱分析1.1加载“ma1_1”语音数据。
基于DFT 变换，画出其中一帧数据（采样频率为8kHz ，帧长为37.5ms ，每帧有300个样点）的频域波形（对数幅度谱）。
load ma1_1;x = ma1_1 (4161:4460); plot (x)N = 1024; k = - N/2:N/2-1;X = fftshift (fft (x.*hann (length (x)),N));plot (k,20*log10 (abs(X))), axis ([0 fix(N/2) -inf inf ])已知该帧信号的时域波形如图（a ）所示，相应的10阶LPC 谱如图（b ）所示。
问题1：这帧语音是清音还是浊音？基于DFT 求出的对数幅度谱和相应的LPC 谱相比，两者有什么联系和区别？问题2：根据这帧基于DFT 的对数幅度谱，如何估计出共振峰频率和基音周期？问题3：时域对语音信号进行加窗，反映在频域，其窗谱对基于DFT 的对数幅度谱有何影响？如何估计出窗谱的主瓣宽度？1.2对于浊音语音，可以利用其频谱)(ωX 具有丰富的谐波分量的特点，求出其谐波乘积谱：∏==R r r X HPSx 1)()(ωω式中，R 一般取为5。
在谐波乘积谱中，基频分量变得很大，更易于估计基音周期。
1.3加载“vowels.mat”语音数据，分别画出一帧/i/和一帧/u/（采样频率为10kHz，帧长为30ms，每帧有300个样点）的基于DFT的对数幅度谱。
其Matlab代码如下：load vowelsx = vowels.i_1(2001:2300);N = 1024; k= -N/2:N/2-1;X = fftshift (fft (x.*hann (length(x)),N));plot (k,20*log10(abs(X))), axis([0 fix(N/2) 0 100])x = vowels.u_1(2001:2300);N= 1024; k = -N/2:N/2-1;X = fftshift (fft (x.*hann(length(x)),N));plot (k,20*log10(abs(X))), axis([0 fix(N/2) 0 100])1.4画出一帧清音语音的基于DFT的对数幅度谱。
利用Matlab进行频谱分析的方法
利用Matlab进行频谱分析的方法引言频谱分析是信号处理和电子工程领域中一项重要的技术，用于分析信号在频率域上的特征和频率成分。
在实际应用中，频谱分析广泛应用于音频处理、图像处理、通信系统等领域。
Matlab是一种强大的工具，可以提供许多功能用于频谱分析。
本文将介绍利用Matlab进行频谱分析的方法和一些常用的工具。
一、Matlab中的FFT函数Matlab中的FFT（快速傅里叶变换）函数是一种常用的频谱分析工具。
通过使用FFT函数，我们可以将时域信号转换为频域信号，并得到信号的频谱特征。
FFT 函数的使用方法如下：```Y = fft(X);```其中，X是输入信号，Y是输出的频域信号。
通过该函数，我们可以得到输入信号的幅度谱和相位谱。
二、频谱图的绘制在进行频谱分析时，频谱图是一种直观和易于理解的展示形式。
Matlab中可以使用plot函数绘制频谱图。
首先，我们需要获取频域信号的幅度谱。
然后，使用plot函数将频率与幅度谱进行绘制。
下面是一个示例：```X = 1:1000; % 时间序列Y = sin(2*pi*10*X) + sin(2*pi*50*X); % 输入信号Fs = 1000; % 采样率N = length(Y); % 信号长度Y_FFT = abs(fft(Y)); % 计算频域信号的幅度谱f = (0:N-1)*(Fs/N); % 频率坐标plot(f, Y_FFT);```通过上述代码，我们可以得到输入信号在频谱上的特征，并将其可视化为频谱图。
三、频谱分析的应用举例频谱分析可以应用于许多实际问题中。
下面将介绍两个常见的应用举例：语音信号分析和图像处理。
1. 语音信号分析语音信号分析是频谱分析的一个重要应用领域。
通过对语音信号进行频谱分析，我们可以探索声波的频率特性和信号的频率成分。
在Matlab中，可以使用wavread 函数读取音频文件，并进行频谱分析。
下面是一个示例：```[waveform, Fs] = wavread('speech.wav'); % 读取音频文件N = length(waveform); % 信号长度waveform_FFT = abs(fft(waveform)); % 计算频域信号的幅度谱f = (0:N-1)*(Fs/N); % 频率坐标plot(f, waveform_FFT);```通过上述代码，我们可以获取语音信号的频谱特征，并将其可视化为频谱图。
基于matlab实现语音信号频谱分析
目录第1章课题的设计要求、目的、意义 (3)1.1课题的设计要求： (3)1.1.1．信号采集 (3)1.1.2．构造受干扰信号并对其进行FFT频谱分析 (3)1.1.3．数字滤波器设计 (3)1.1.4．信号处理 (3)1.1.5．设计图形用户界面 (3)1.2课题的设计目的与意义： (3)第2章课程设计报告内容 (4)2.1理论依据 (4)2.2信号采集 (4)2.3构造一个正弦干扰信号来干扰语音信号 (4)2.4数字滤波器设计 (4)2.5信号处理 (4)2.6具体指标 (4)2.7设计图形用户界面 (4)第3章设计理论依据 (5)3.1采样定理 (5)3.2采样频率 (5)第4章图形用户界面制作及Matlab实现 (6)4.1 按钮、静态文本和编辑器的使用 (6)4.1.1打开guide (6)4.2 按钮与程序的联系 (8)第5章调试及分析 (8)5.1打开信号。
(8)5.2声音播放，同时显示波形。
(9)5.3语音信号的频谱、幅度和相位。
(10)5.3.1频谱。
(10)5.3.2幅度。
(10)5.3.3相位。
(11)5.4加噪声后的语音信号波形。
(12)5.5加噪声后的语音信号的频谱、幅度和相位。
(12)5.5.1频谱。
(12)5.5.2幅度。
(13)5.5.3相位。
(13)5.6信号通过FIR滤波器后的波形。
(14)5.7信号通过FIR滤波器后的频谱、幅度和相位。
(15)5.7.1频谱。
(15)5.7.2幅度。
(16)5.7.3相位。
(16)5.8信号通过IIR滤波器后的波形。
(17)5.9 信号通过IIR滤波器后的频谱、幅度和相位。
(18)5.9.1频谱。
(18)5.9.2幅度。
(18)5.9.3相位。
(19)5.10信号通过巴特沃斯滤波器后的波形。
(20)5.11 信号通过巴特沃斯滤波器后的频谱、幅度和相位。
(21)5.11.1频谱。
基于MATLAB的语音频域特征分析
经典功率谱估计与现代功率谱估计的对比 [摘要]本文主要介绍了在MATLAB环境下，从介绍功率谱的估计原理入手分析了经典谱估计和现代谱估计两类估计方法的原理、各自特点以及实现方法。
[关键词]功率谱；功率谱估计；经典功率谱估计；现代功率谱估计；语谱图；共振峰信号的频谱分析是研究信号特性的重要手段之一，通常是求其功率谱来进行频谱分析。
功率谱反映了随机信号各频率成份功率能量的分布情况，可以揭示信号中隐含的周期性及靠得很近的谱峰等有用信息，在许多领域都发挥了重要作用。
然而，实际应用中的平稳随机信号通常是有限长的，只能根据有限长信号估计原信号的真实功率谱，这就是功率谱估计。
⑴功率谱估计cleara=wavread('鸟语花香.wav');subplot(2,1,1),plot(a);title('original signal');grid;N=256;h=hamming(N);for m=1:Nb(m)=a(m)*h(m);endy=20*log(abs(fft(b)));subplot(2,1,2);plot(y);title('短时谱');xlabel('频率(Hz)');ylabel('功率谱(db)');grid;①%相关法：相关法是利用维纳-辛钦定理该方法先由序列x(n)估计出自相关函数R（n），然后对R(n)进行傅立叶变换，便得到x(n)的功率谱估计。
[xn,Fs,bits]=wavread('鸟语花香.wav');n=0:1/Fs:1;nfft=512;cxn=xcorr(xn,'unbiased');CXk=fft(cxn,nfft);Pxx=abs(CXk);index=0:round(nfft/2-1);k=index*Fs/nfft;a=log(10);b=log(Pxx(index+1));c=b/a;plot_Pxx=10*c;plot(k,plot_Pxx);xlabel('frequeney（hz）相关法');ylabel('power spectraldensity');title('recorrelation psd estimate');②周期图法周期图法是直接将信号的采样数据x(n)进行Fourier 变换求取功率谱密度估计的方法。
基于MATLAB实现对语音信号频谱分析
的起点移至 处截取信号 ，再做傅里叶变换而得到
的一个频谱函数。这是直接将频率轴方向来理解的。
另一种解释是从时间轴方向来理解，当频率固定时，
例如
，则
可以看作是信号经过一个中心频
率为 的带通滤波器产生的输出。这是因为窗口函数
通常具有低通频率响应，而指数 对语音信号
有调制的作用，使频谱产生移位，即将 频谱中
对应于频率 的分量平移到零频。
3、短时傅里叶反变换(倒谱分析)
傅里叶变换建立了信号从时域到频域的变换桥
梁，而傅里叶反变换则建立了信号从频域到时域的
变换桥梁这两个域之间的变换为一对一映射关系。
我们知道，
可以看作是加窗后函数的傅里叶变
换，为了实现反变换，将
进行频率采样，即令
图2 频谱分析过程
，则有
2、短时傅里叶变换(频谱分析)
公司推出的一种面向工程和科学计算的交互式计算软 的录音机功能可以用麦克风直接录制一段女声“世界
件，它以矩阵运算为基础，把计算、可视化、程序设 上最遥远的距离不是生与死，而是我就站在你面前
计融合到了一个简单易用的交互式工作环境中。同时 你确不知道我爱你”，并保存为WAV 格式文件，供
由于Matlab是一个数据分析和处理功能十分强大的工程 MATLAB 相关函数直接读取、写入或播放。本文以
三、语音信号分析及MATLAB的实现 1、语音信号的频谱分析过程 傅里叶频谱分析是语音信号频域分析中广泛采用的 一种方法。语音波是一个非平稳过程，因此适用于周 期、瞬变或平稳随机信号的标准傅里叶变换不能直接 表示语音信号，而应该用短时傅里叶变换对语音信号 的频谱进行分析，相应的频谱称为“短时谱”。 进行频谱分析时，在时域数据进行短时FFT处理之 前都要进行加窗处理。在FFT处理之后，普通频谱分析 可以进行频域上的滤波处理，从而使频谱更加平滑。 最后IFFT处理观察恢复后的时域信号图形，频谱分析过 程(如图2所示)。
基于MATLAB的语音信号时域特征分析(
基于MATLAB 的语音信号时域特征分析研究背景及意义：语音信号是一种非平稳的时变信号，它携带着各种信息。
在语音编码、语音合成、语音识别和语音增强等语音处理中无一例外需要提取语音中包含的各种信息。
语音信号分析的目的就在与方便有效的提取并表示语音信号所携带的信息。
语音信号分析可以分为时域和变换域等处理方法，其中时域分析是最简单的方法，直接对语音信号的时域波形进行分析，提取的特征参数主要有语音的短时能量，短时平均过零率, 短视自相关函数。
短时自相关函数自相关函数用于衡量信号自身时间波形的相似性。
清音和浊音的发声机理不同，因而在波形上也存在着较大的差异。
浊音的时间波形呈现出一定的周期性，波形之间相似性较好；清音的时间波形呈现出随机噪声的特性，样点间的相似性较差。
因此，我们用短时自相关函数来测定语音的相似特性。
短时自相关函数定义为：()()()()()n m R k x m w n m x m k w n m k ∞=-∞=-+--∑令'm n m =+´，并且'()()w m w m -=，可以得到：1''''()[()()][()()][()()][()()]N k n m m R k x n m w m x n m k w m k x n m w m x n m k w m k ∞--=-∞==++++=++++∑∑ 图1给出了清音的短时自相关函数波形，图7给出了不同矩形窗长条件下（窗长分别为N=70，N=140，N=210，N=280）浊音的短时自相关函数波形。
由图1.1、图1.2短时自相关函数波形分析可知：清音接近于随机噪声，清音的短时自相关函数不具有周期性，也没有明显突起的峰值，且随着延时k 的增大迅速减小；浊音是周期信号，浊音的短时自相关函数呈现明显的周期性，自相关函数的周期就是浊音信号的周期，根据这个性质可以判断一个语音信号是清音还是浊音，还可以判断浊音的基音周期。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
由于语音信号是短时平稳的随机信号 ， 某一语音 信号帧的短时傅立叶变换的定义为 ：
∞
（ ） ∑ （ （ — ｅ ＝ ｍ） ｎ ｍ）
（． ） ２ １
以分辨 由于激励所形成的细微结构 ， 称为宽带语谱图； 而窄带语谱 图正好 与之相反。 宽带语谱图可以获得较高 的时间分辨率 ， 反映频
２ １ 年 ８月 ０１
湖北第二师范学院学报
Ｊ ｕｎ ｌｏ ｂ ｉＵｍｖ ｍｉ ｏ ｕ ａ ｏ ｏ ｒ ａ ｆＨｕ ｅ ｅ ￣ ｆＥｄ ｃ ｔ ｎ ｉ
Ａｌ ２ １ 唱． ０ １
第 ２ 卷第 ８ ８ 期
Ｖ０． ８ Ｎｏ ８ １２ ．
基 于 ＭＡ Ｌ Ｂ分 析 语 音信 号 频 域 特 征 ＴＡ
谱、 倒谱 ， 画出语谱 图， 并分析仿 真结果 ， 在此基础上 ， 借助频域分析方法所求得的参数分析语音信号的基音
周期或共振峰。 ２ 语音分 析基本 方法
２ １ 短 时傅 立 叶变换 ．
音信号 的动态频率特性 ， 在语音 分析 中具有重要的实 用价值。被成为可视语言。 语谱 图的时间分辨率和频率分辨率是由窗 函数的 特性决定的。时间分辨率高 ， 以看 出时间波形的每 可 个周期及共振峰随时间的变化 ， 但频率分辨率低， 不足
于是 可 以得 到
∞
．
带两与语音特性相关 的信息 。语谱图上 因其不 同的灰 度， 形成不 同的纹路 ， 称之为“ 声纹” 。声纹因人而异 ， 因此可 以在司法 、 安全等场合得到应用 。
收 稿 日期 ：０ １ ０ ２ ２ １ — ６— ８
・
瓦 （ ） ｅ ＝ ＝一 ．
作者简介 ： 肖正安（ ９６一） 男 ， １７ ， 湖北钟祥人 ， 讲师 ， 硕士 ， 究方 向为数 字信号 处理及通信 电子线路 。 研
１ 引 言
假定
∞
信号的傅立叶表示在信号 的分析与处理中起着重 要的作用。因为对于线性系统来说 ， 可以很方便地确
定其对正弦或复指数和的响应 ， 以傅立 叶分析方法 所
Ｃ ｎ ｚ ［ ｎｘ（） ］ （ ）＝ １ Ｉ ｚ １ （．） ２ ８
图 ３ １ 短 时谱 ．
在时域上， 语音产生模型实 际上是一个激励信号 与声道冲激响应 的卷 积。对于浊音 ， 激励信号可 以由
周期脉冲序列表示 ； 对于清音 ， 激励信号可 以由随机噪 声序列表示 。声道系统相当于参数缓慢变化的零极点
（ ） （ Ｊ ｋ ｘ —｝ ）
（．） ２３
３ ・ ５
２ ３ 复倒 谱 和倒谱 ．
复倒 谱 （ ） ｘ ｎ 的 曼＝ ［ｎ Ｘ ｎ ］ Ｚ １Ｚ［ （ ） ］ （．） ２７
倒谱 Ｃｎ 定义为 ｘ ｎ 取 ｚ变换后 的幅度对数的 （） （） 逆 Ｚ变换 ， 即
谱 的快速时变过程 ； 窄带语谱图可以获得较高 的频率 分辨率 ， 反映频谱的精细结构 。两者相结合 ， 以提供 可
其 中 Ｗ ｎ ｍ 是实窗 口函数序列 ， （— ） ｎ表示某一语音信 号帧。令 ｎ ｎ＝ ’则得到 —ｌ ｋ ，
∞
蜀 （ ）＝． ｗ ｋ ） （ ｜ ） 一 【 （ ．） ， ∑ （ ’ 一ｊ ｅ ｎ ’２ ２ ｝ ’ —
（ １ １—ｍ） 一 ｍ）１ ＇ ３ｔ （ ｅ
Ｊ ＝ ｎ 一 ∞
，０ ≤Ⅳ一１ （ ≤ ） （ ．） ２６
稳随机信号的表示 ， 但不能直接用于语音信号 。由于
语音信号可以认为在短时间内， 近似不变， 因而可 以采 ２２ 语谱图 ． 用短时分析法。 水平方 向是时间轴 ， 垂直方向是频率轴 ， 图上的灰 本文从傅里叶分析原理 出发 ， 编写程序估计 短时 度条纹代表各个时刻 的语 音短时谱 。语谱图反映了语
肖正 安
（ 北 第二 师 范学 院 物理 与 电子信 息学 院 ， 汉 ４ ００ ） 湖 武 ３ ２５
摘 要： 语音信号的频域分析 包括语音信号 的频谱 、 功率谱 、 倒频谱 、 频谱 包络分析等 ， 常用的频域分析 方法有带通 滤 而
波器组法、 里叶变换法、 傅 线性参 见测法等几种。本文采用傅里叶 变换 法结合 ｍ ｔｂ讨论 了一段语音信 号的短 时谱 、 ａａ ． １ 语
谱 图、 倒谱 和复制谱 等特 征 ， 出了基 音周期及 共振峰等仿真结果。 给
关键词 ： Ｔ Ａ 频谱 分析 ； 时傅 里叶变换 ； ＭＡ Ｌ Ｂ； 短 复倒谱 中图分类号 ：Ｎ １． Ｔ ９２ ３ 文献标 识码 ： Ａ 文章编号 ：６ ４３４ ２ １ ） ８０ ３ －３ １７ －４ Ｘ（０ １ ０ －（ ５０ ２
瓦 （ ） ｅ 嚣（ ） ＝ （．） ２５ 同样 ， 不同的窗 口函数 ， 将得到不同的傅立叶变换
式的结果。由上式可见 ， 短时傅立叶变换有两个变量 ： ｎ ∞ 所以它既是时序 １的离散函数 ， 和 ， 又是角频率 ∞
的连续 函数 。与离 散傅立 叶变换逼近傅立 叶变换一 是一个受准周期脉冲或随机躁声源激励的线性系统的 样， 如令 ∞＝ ， ／ 则得离散的短时傅立叶吧如下 ： ２ｒ Ｎ， ｒ ｋ 输出。输出频谱是声道系统频率响应与激励源频谱的 ｘ（ ｎ ）＝ ｎ ｋ Ｘ （ ）＝ 乘积 。声道系统 的频率响应及激励源都是随时间变化 的， 因此一般标准的傅立叶表示虽然适用于周期及平
（ ） ＝．
（）（ ｊｅ Ｊ —｝ ， ｝ ）’ 础
（．） ２４
则可 以得到
能完善地解决许多信号分析和处理问题 。另外 ， 傅立 叶表示使信号 的某些特性变得更明显 ， 因此 ， 它能更深 入地说明信号 的各项物理现象 。 由于语音信号是随着时间变化的， 通常认为 ， 语音