数学建模实验四:Matlab神经网络以及应用于汽油辛烷值预测
数学建模实验三:Matlab神经网络以及应用于汽油辛烷值预测

实验三Matlab神经网络以及应用于汽油辛烷值预测一、实验目的1. 掌握MATLAB创建BP神经网络并应用于拟合非线性函数2. 掌握MATLAB创建REF神经网络并应用于拟合非线性函数3. 掌握MATLAB创建BP神经网络和REF神经网络解决实际问题4. 了解MATLAB神经网络并行运算二、实验原理2.1 BP神经网络2.1.1 BP神经网络概述BP神经网络Rumelhard和McClelland于1986年提出。
从结构上将,它是一种典型的多层前向型神经网络,具有一个输入层、一个或多个隐含层和一个输出层。
层与层之间采用权连接的方式,同一层的神经元之间不存在相互连接。
理论上已经证明,具有一个隐含层的三层网络可以逼近任意非线性函数。
隐含层中的神经元多采用S型传递函数,输出层的神经元多采用线性传递函数。
图1所示为一个典型的BP神经网络。
该网络具有一个隐含层,输入层神经元数据为R,隐含层神经元数目为S1,输出层神经元数据为S2,隐含层采用S型传递函数tansig,输出层传递函数为purelin。
图1含一个隐含层的BP网络结构2.1.2 BP神经网络学习规则BP网络是一种多层前馈神经网络,其神经元的传递函数为S型函数,因此输出量为0到1之间的连续量,它可以实现从输入到输出的任意的非线性映射。
由于其权值的调整是利用实际输出与期望输出之差,对网络的各层连接权由后向前逐层进行校正的计算方法,故而称为反向传播(Back-Propogation)学习算法,简称为BP算法。
BP算法主要是利用输入、输出样本集进行相应训练,使网络达到给定的输入输出映射函数关系。
算法常分为两个阶段:第一阶段(正向计算过程)由样本选取信息从输入层经隐含层逐层计算各单元的输出值;第二阶段(误差反向传播过程)由输出层计算误差并逐层向前算出隐含层各单元的误差,并以此修正前一层权值。
BP网络的学习过程主要由以下四部分组成:1)输入样本顺传播输入样本传播也就是样本由输入层经中间层向输出层传播计算。
基于数据挖掘的汽油精制过程辛烷值损失预测模型
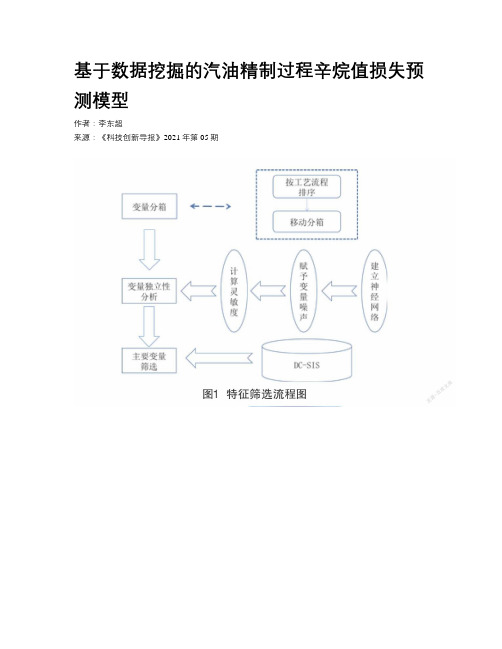
基于数据挖掘的汽油精制过程辛烷值损失预测模型作者:***来源:《科技创新导报》2021年第05期摘要:汽油精制过程中造成的辛烷值损失会降低汽油的燃烧效率,如何降低汽油精制过程中辛烷值的损失量是目前相关企业面临的一个重要课题。
本文利用我国某石化企业在催化裂化汽油精制过程中积累的数据,建立基于神经网络、测量误差模型以及DC-SIS数据降维方法的两阶段特征筛选模型,选择出对辛烷值影响比较大的因素。
设计了一种基于XGBoost和神经网络的辛烷值预测模型,可以实现对不同原材料和不同操作下精制后辛烷值的预测,经验证,模型的均方误差为0.06876,所设计模型在处理辛烷值预测问题时可以达到比较好的预测效果。
关键词:辛烷值高维降维测量误差模型神经网络 XGBoost中图分类号:TP274 文獻标识码:A 文章编号:1674-098X(2021)02(b)-0092-05Prediction Model of Octane Number Loss in Gasoline Refining Process Based on Data Mining LI Dongchao(School of Mathematics and Statistics, Nanjing University of Information Science & Technology, Nanjing, Jiangsu Province, 210044 China)Abstract: The loss of octane number in the process of gasoline refining will reduce the combustion efficiency of gasoline. How to reduce the loss of octane number in the process of gasoline refining is an important issue facing related enterprises. This paper uses the data accumulated by a petrochemical enterprise during the refining process of catalytic cracking gasoline to establish a two-stage feature screening model based on neural network, measurement error model and DC-SIS data dimensionality reduction method, and select the one that has a greater impact on the octane number factor. An octane number prediction model based on XGBoost and neural network is designed,which can predict the octane number after refining under different raw materials and different operations. After verification, the mean square error of the model is 0.06876. A better prediction effect can be achieved in the alkane number prediction problem.Key Words: Octane number; High dimensionality reduction; Neural networks; XGBoost汽油是小型车辆的主要燃料,汽油燃烧产生的尾气排放对大气环境有重要影响。
数学建模实验四:Matlab神经网络以及应用于汽油辛烷值预测

实验四:Matlab 神经网络以及应用于汽油辛烷值预测专业年级: 2014级信息与计算科学1班姓名: 黄志锐 学号:201430120110一、实验目的1. 掌握MATLAB 创建BP 神经网络并应用于拟合非线性函数2. 掌握MATLAB 创建REF 神经网络并应用于拟合非线性函数3. 掌握MATLAB 创建BP 神经网络和REF 神经网络解决实际问题4. 了解MATLAB 神经网络并行运算二、实验内容1. 建立BP 神经网络拟合非线性函数2212y x x =+第一步 数据选择和归一化根据非线性函数方程随机得到该函数的2000组数据,将数据存贮在data.mat 文件中(下载后拷贝到Matlab 当前目录),其中input 是函数输入数据,output 是函数输出数据。
从输入输出数据中随机选取1900中数据作为网络训练数据,100组作为网络测试数据,并对数据进行归一化处理。
第二步 建立和训练BP 神经网络构建BP 神经网络,用训练数据训练,使网络对非线性函数输出具有预测能力。
第三步 BP 神经网络预测用训练好的BP 神经网络预测非线性函数输出。
第四步 结果分析通过BP 神经网络预测输出和期望输出分析BP 神经网络的拟合能力。
详细MATLAB代码如下:27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54disp(['神经网络的训练时间为', num2str(t1), '秒']);%% BP网络预测% 预测数据归一化inputn_test = mapminmax('apply', input_test, inputps); % 网络预测输出an = sim(net, inputn_test);% 网络输出反归一化BPoutput = mapminmax('reverse', an, outputps);%% 结果分析figure(1);plot(BPoutput, ':og');hold on;plot(output_test, '-*');legend('预测输出', '期望输出');title('BP网络预测输出', 'fontsize', 12);ylabel('函数输出', 'fontsize', 12);xlabel('样本', 'fontsize', 12);% 预测误差error = BPoutput-output_test;figure(2);plot(error, '-*');title('BP神经网络预测误差', 'fontsize', 12);ylabel('误差', 'fontsize', 12);xlabel('样本', 'fontsize', 12);figure(3);plot((output_test-BPoutput)./BPoutput, '-*');title('BP神经网络预测误差百分比');errorsum = sum(abs(error));MATLAB代码运行结果截图如下所示:MATLAB代码运行结果如下所示:图1 BP神经网络预测输出图示图2 BP神经网络预测误差图示图3 BP 神经网络预测误差百分比图示2. 建立RBF 神经网络拟合非线性函数22112220+10cos(2)10cos(2)y x x x x ππ=-+-第一步 建立exact RBF 神经网络拟合, 观察拟合效果详细MATLAB 代码如下:MATLAB代码运行结果如下所示:图4 RBF神经网络拟合效果图第二步建立approximate RBF神经网络拟合详细MATLAB代码如下:13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41F = 20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2); %% 建立RBF神经网络% 采用approximate RBF神经网络。
应用BP神经网络的二次反应清洁汽油辛烷值预测_周小伟

积分数不大于 35% , w ( S) [ 150 @ 10- 6 [ 1] . 但是, 我 国常规( 流化催化裂化) 工艺生产的汽油中烯烃体积 分数高达 45% ~ 60% , 而且我国车用汽油中的流化 催化裂化( F CC) 汽油占 78% 以上, 有些炼油厂几乎 占 100% . 因此, 降低 F CC 汽油的烯烃 含量已成为 生产清洁汽油的关键. 汽油二次反应[ 2O3] 是能同时降
图 1 BP 神经网络结构示意图
第一层是输入节点, 最后一层是输出节点, 其间 有一层或多层隐含层节点, 各层内的节点间无连接, 信息仅单方向流动. BP 神经网络的训练方法是通过 反向误差传播原理不断调整网络权值, 从而使得实 际输出与期望输出之间的误差平方和达到最小或小 于某个阈值. 其训练或学习过程由正向传播和反向 传播两部分构成. 当正向传播时, 信息从输入层经隐 含处理后传入输出层, 每一层神经元状态只影响下 一层的神经元的状态. 如果在输出层得不到希望的 输出, 则转入反向传播, 将误差信号沿原来的神经元 连接通路返回. 在返回过程中, 逐一修改各神经元连 接的权值, 经过不断的迭代, 最后使信号误差达到允 许范围之内. 算法的步骤如下.
摘要: 借鉴复杂反应动力学研究中的集总方法, 将汽油辛烷值看成汽油链烷烃集总、环烷烃集总、 芳烃集总、烯烃集总的函数. 采用多元线性回归和 BP 神经网络算法, 分别建立了二次反应清洁汽 油的研究法辛烷值预测模型, 并进行了实例计算验证和对比分析. 结果表明, BP 神经网络模型的整 体性能优于多元线性回归模型, 其强大的非线性映射能力能够更好地反映汽油研究法辛烷值与各 集总组分之间的复杂关系, 且具有更好的预测性能, 模型预测值与实验测得的汽油辛烷值的平均相 对误差为 01 39% , 与文献报道的汽油辛烷值的平均相对误差为 01 92% . 关键词: 清洁汽油; 辛烷值; 集总; 多元线性回归; BP 神经网络 中图分类号: T Q622; T P3011 6 文献标志码: A 文章编号: 0253O987X( 2010) 12O0082O05
基于Matlab的自组织神经网络在油气层识别中的应用研究

中幽分类号 :P 9 T 39
文献标识码 : A
文章编号 :0 9 34 (063 - 19 0 10— 0 420 )5 0 1_ 3
O¨& Ga omai e ti t nB s do e - g n ainN ua N t r f t b sF r t n I ni ai a e nS l Ora i t e rI ewoko l o d f o c f z o Ma a WANGJ — u, I h y n , HOU un W a h a L i og Z i Z — G a— U
n u a n t o k a d s l r a ia o p ig n u a e o k ae c mp r d we o t z h aa t ro e t cu e a d ma e t e cut r e rl e w r n ef g nz t n ma p n e rln t r r o ae . -o i w p i e t e p r mee fn ts u t r k h l s mi r n e
aayi o p tsmpe O i a a f qn s sd t ul e ok mo e. Th aa tr o e ok s u tr r p mie 。 a dte n ls f n u s i a l. l s t o igi u e ob i n t r d 1 —g d a Da d w ep rmees f t r r cueaeo t z d n nw t i h cutra a s fn smpei mae Th euto t n ls h wsta l eh d o l ra ia o Oh e t en ua e o ka d ls n l i o p a l S d . e y s i ersl fda a a i so htt em to f ef g nzt n C tp t v e r n t r n a ys l s -o i i i l w
应用BP神经网络的二次反应清洁汽油辛烷值预测

应用BP神经网络的二次反应清洁汽油辛烷值预测
周小伟;袁俊;杨伯伦
【期刊名称】《西安交通大学学报》
【年(卷),期】2010(044)012
【摘要】借鉴复杂反应动力学研究中的集总方法,将汽油辛烷值看成汽油链烷烃集总、环烷烃集总、芳烃集总、烯烃集总的函数.采用多元线性回归和BP神经网络算法,分别建立了二次反应清洁汽油的研究法辛烷值预测模型,并进行了实例计算验证和对比分析.结果表明,BP神经网络模型的整体性能优于多元线性回归模型,其强大的非线性映射能力能够更好地反映汽油研究法辛烷值与各集总组分之间的复杂关系,且具有更好的预测性能,模型预测值与实验测得的汽油辛烷值的平均相对误差为0.39%,与文献报道的汽油辛烷值的平均相对误差为0.92%.
【总页数】5页(P82-86)
【作者】周小伟;袁俊;杨伯伦
【作者单位】西安交通大学能源与动力工程学院,710049,西安;西安近代化学研究所,710065,西安;西安交通大学能源与动力工程学院,710049,西安
【正文语种】中文
【中图分类】TQ622;TP301.6
【相关文献】
1.基于BP神经网络的堆石坝参数二次反演与变形预测 [J], 程壮;陈星;董艳华;党莉
2.基于LM/SVM方法的二次反应清洁汽油辛烷值预测 [J], 袁俊;周小伟;杨伯伦
3.基于BP神经网络对汽油辛烷值损失预测模型的构建 [J], 王宁宁
4.基于BP神经网络对汽油辛烷值损失预测模型的构建 [J], 王宁宁
5.基于PLS-MI组合的天牛须搜索BP神经网络模型对汽油辛烷值的预测性能 [J], 石翠翠;刘媛华
因版权原因,仅展示原文概要,查看原文内容请购买。
汽油调合优化神经网络模型的研究

汽油调合优化神经网络模型的研究
近几年来,随着我国经济的发展,汽油的需求量不断增加,汽油的质量要求也随之提高。
汽油的质量主要由其组分(例如烷烃、芳香烃、Alkene等)的比例来决定。
为了确保汽油的质量,汽油的调合必须恰到好处,这需要汽油的调合参数可以得到精确的掌握。
神经网络是一种智能的机器学习算法,它可以通过训练获取大量数据,从而使模型有较强的拟合能力和泛化能力。
因此,把神经网络用于汽油调合优化是科学、可行的。
本文分析了汽油调合优化神经网络模型的原理,把神经网络模型应用到汽油调合优化研究中,并且利用数值仿真与实验结果来验证模型的准确性。
首先,本文介绍了神经网络模型的结构,包括网络的输入层、隐层和输出层。
神经网络模型的输入层是汽油的调合参数,隐层是神经元,输出层是汽油的质量指标。
其次,本文利用BP神经网络模型进行汽油调合优化,首先根据汽油的调合参数,建立组分比例与汽油质量指标之间的关系模型,然后在数据库中获取大量数据,训练神经网络模型,模型最终能够正确地预测出给定组分比例下汽油的质量指标。
最后,本文通过数值仿真与实验结果来验证模型的准确性。
数值仿真的结果显示,汽油质量指标与给定组分比例的变化趋势一致,证明神经网络模型可以很好地模拟汽油调合过程;实验结果表明,模型计算结果与实际测试结果基本一致,验证了模型的准确性。
综上所述,运用神经网络模型可以帮助汽油调合优化研究者更有效、更准确地预测汽油的质量指标,从而提高汽油的调合效率和质量。
6-有导师学习神经网络的回归拟合

基础理论
神经网络的学习规则又称神经网络的训练算法,用来计算
更新神经网络的权值和阈值。学习规则有两大类别:有导师学
习和无导师学习。在有导师学习中,需要为学习规则提供一系 列正确的网络输入/输出对(即训练样本),当网络输入时,将 网络输出与相对应的期望值进行比较,然后应用学习规则调整
RBF具体步骤
(1)确定隐含层神经元径向基函数中心
C P'
(2)确定隐含层神经元阈值
b1 [b11 , b12 ,, b1Q ]'
其中, b11 b12 b1Q
0.8326 spread
spread为径向基函数的扩展速度。 (3)确定隐含层与输出层间权值和阈值
ai exp( C pi bi )
油样品近红外光谱与辛烷值间的数学模型,并对模型进行评价。
的,即网络的输出是隐含层神经元输出的线性加权和。
权值和阈值由线性方程组直接解出。
典型的RBF神经网络结构如图所示
IW1,1 dist
a1
LW1,2
a2
*
b2
+
b1
a1 radbas ( IW1,1 p b1 )
输入层 隐含层
a 2 purelin( LW 2,1a1 b2 )
输出层
n n l m 2
BP网络函数命令
(1) BP神经网络创建
net =
newff(P,T,[S1 S2 … S(N-1)],{TF1 TF2 …TFN1}, …
BTF,BLF,PF,IPF,OPF,DDF)
(2) BP神经网络训练函数
[net,tr,Y,E,Pf,Af] = train (net,P,T,Pi,Ai)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四:Matlab 神经网络以及应用于汽油辛烷值预测专业年级: 2014级信息与计算科学1班姓名: 黄志锐 学号:0110一、实验目的1. 掌握MATLAB 创建BP 神经网络并应用于拟合非线性函数2. 掌握MATLAB 创建REF 神经网络并应用于拟合非线性函数3. 掌握MATLAB 创建BP 神经网络和REF 神经网络解决实际问题4. 了解MATLAB 神经网络并行运算二、实验内容1. 建立BP 神经网络拟合非线性函数2212y x x =+第一步 数据选择和归一化根据非线性函数方程随机得到该函数的2000组数据,将数据存贮在文件中(下载后拷贝到Matlab 当前目录),其中input 是函数输入数据,output 是函数输出数据。
从输入输出数据中随机选取1900中数据作为网络训练数据,100组作为网络测试数据,并对数据进行归一化处理。
第二步 建立和训练BP 神经网络构建BP 神经网络,用训练数据训练,使网络对非线性函数输出具有预测能力。
第三步 BP 神经网络预测用训练好的BP 神经网络预测非线性函数输出。
第四步 结果分析通过BP 神经网络预测输出和期望输出分析BP 神经网络的拟合能力。
详细MATLAB代码如下:27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54disp(['神经网络的训练时间为', num2str(t1), '秒']); %% BP网络预测% 预测数据归一化inputn_test = mapminmax('apply', input_test, inputps); % 网络预测输出an = sim(net, inputn_test);% 网络输出反归一化BPoutput = mapminmax('reverse', an, outputps);%% 结果分析figure(1);plot(BPoutput, ':og');hold on;plot(output_test, '-*');legend('预测输出', '期望输出');title('BP网络预测输出', 'fontsize', 12);ylabel('函数输出', 'fontsize', 12);xlabel('样本', 'fontsize', 12);% 预测误差error = BPoutput-output_test;figure(2);plot(error, '-*');title('BP神经网络预测误差', 'fontsize', 12);ylabel('误差', 'fontsize', 12);xlabel('样本', 'fontsize', 12);figure(3);plot((output_test-BPoutput)./BPoutput, '-*');title('BP神经网络预测误差百分比');errorsum = sum(abs(error));MATLAB代码运行结果截图如下所示:MATLAB代码运行结果如下所示:图1 BP神经网络预测输出图示图2 BP神经网络预测误差图示图3 BP 神经网络预测误差百分比图示2. 建立RBF 神经网络拟合非线性函数22112220+10cos(2)10cos(2)y x x x x ππ=-+-第一步 建立exact RBF 神经网络拟合, 观察拟合效果详细MATLAB 代码如下:MATLAB代码运行结果如下所示:图4 RBF神经网络拟合效果图第二步建立approximate RBF神经网络拟合详细MATLAB代码如下:13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41F = 20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2); %% 建立RBF神经网络% 采用approximate RBF神经网络。
spread为默认值net = newrb(x, F);%% 建立测试样本% generate the testing datainterval = ;[i, j] = meshgrid:interval:;row = size(i);tx1 = i(:);tx1 = tx1';tx2 = j(:);tx2 = tx2';tx = [tx1; tx2];%% 使用建立的RBF网络进行模拟,得出网络输出ty = sim(net, tx);%% 使用图像,画出3维图% 真正的函数图像interval = ;[x1, x2] = meshgrid:interval:;F = 20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2); subplot(1, 3, 1);mesh(x1, x2, F);zlim([0, 60]);title('真正的函数图像')% 网络得出的函数图像v = reshape(ty, row);subplot(1, 3, 2);mesh(i, j, v);MATLAB代码运行结果截图如下所示:MATLAB代码运行结果如下所示:图5 RBF神经网络拟合结果图示讨论题:对于非线性函数220.252220.11212(){sin [50()]1}y x x x x =+⋅++(1)分别建立BP 神经网络和RBF 神经网络拟合并比较两者的性能差异。
(2)就BP 神经网络验证单线程运算和并行运算的运行时间差异。
(1)详细MATLAB 代码如下:MATLAB代码运行结果截图如下所示:MATLAB代码运行结果如下所示:图6 BP神经网络拟合效果图详细MATLAB代码如下:MATLAB代码运行结果如下所示:图7 RBF神经网络拟合效果图详细MATLAB代码如下:5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33% 产生2*sample的随机矩阵,随机数在区间[a, b]中a = -2;b = 2;x = a + (b-a).*rand(2, sample);% 计算网络输出y值y = f(x(1, :), x(2, :));%% 训练数据归一化input_train = x;output_train = y;[input_n, input_ps] = mapminmax(input_train);[output_n, output_ps] = mapminmax(output_train);%% 构建和训练BP神经网络% BP神经网络构建hiddenSizes = 500;trainFcn = 'trainlm';% net = newff(input_n, output_n, hiddenSizes);net = fitnet(hiddenSizes,trainFcn);= 300;= ;= ;net = train(net, input_n, output_n);%% BP网络预测input_test = a + (b-a).*rand(2, sample*;output_test = f(input_test(1, :), input_test(2, :)); inputn_test = mapminmax('apply', input_test, input_ps); prediction = sim(net, inputn_test);BP_output = mapminmax('reverse', prediction, output_ps); %% 结果分析figure(1);34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62plot(BP_output, ':og');hold on;plot(output_test, '-*');legend('预测输出', '期望输出');title('BP网络预测输出', 'fontsize', 12);ylabel('函数输出', 'fontsize', 12);xlabel('样本', 'fontsize', 12);% 预测误差error = BP_output-output_test;figure(2);plot(error, '-*');title('BP神经网络预测误差', 'fontsize', 12); ylabel('误差', 'fontsize', 12);xlabel('样本', 'fontsize', 12);figure(3);plot((output_test-BP_output)./BP_output, '-*'); title('BP神经网络预测误差百分比');errorsum = sum(abs(error));%% 使用图像,画出3维图% 真正的函数图像interval = ;[x1, x2] = meshgrid(a:interval:b);y = f(x1, x2);subplot(1, 3, 1);mesh(x1, x2, y);zlim([-2, 5]);title('真正的函数图像')% 网络得出的函数图像tx1 = x1(:);MATLAB代码运行结果如下所示:图8 BP神经网络预测输出图示图9 BP神经网络预测误差图示图10 BP神经网络拟合效果图详细MATLAB代码如下:13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41spread = ;net = newrb(x, F, spread );%% 建立测试样本interval = ;[i, j] = meshgrid(a:interval:b);row = size(i);tx1 = i(:);tx1 = tx1';tx2 = j(:);tx2 = tx2';tx = [tx1; tx2];%% 使用建立的RBF网络进行模拟,得出网络输出ty = sim(net, tx);%% 使用图像,画出3维图% 真正的函数图像interval = ;[x1, x2] = meshgrid(a:interval:b);F = f(x1, x2);subplot(1, 3, 1);mesh(x1, x2, F);zlim([-2, 5]);title('真正的函数图像')% 网络得出的函数图像v = reshape(ty, row);subplot(1, 3, 2);mesh(i, j, v);zlim([-2, 5]);title('RBF神经网络结果')% 误差图像MATLAB 代码运行结果如下所示:图11 RBF 神经网络拟合效果图通过分析上述结果可知,对于非线性函数220.252220.11212(){sin [50()]1}y x x x x =+⋅++RBF 神经网络(spread 值为)的拟合效果比BP 神经网络(隐含层神经元的个数为500个)的拟合效果更好,且RBF 神经网络性能更佳(耗时更少)。
