一次移动平均法和一次指数平滑法线性二次移动平均法培训课件
移动平均与指数平滑

— 203.8 206.9 213.8 216.8 218.0 212.1 210.8 216.1 213.2 217.3 226.5
— 203.8 209.0 230.0 226.9 223.8 211.1 209.5 219.0 212.8 219.8 233.8
设时间序列为x1,x2, …: 移动平均法可以表示为:
( xt xt 1 xt N 1 ) 1 t Ft 1 xi N N t N 1
式中:
xt为最新观察值; Ft+1为下一期预测值;
由移动平均法计算公式可以看出,每一新预测值是对
前一移动平均预测值的修正,N越大平滑效果愈好。
(1)移动平均法有两种极端情况
在移动平均值的计算中包括的过去观察值的实
际个数N=1,这时利用最新的观察值作为下一期
的预测值;
N=n ,这时利用全部 n个观察值的算术平均值作
为预测值。
当数据的随机因素较大时,宜选用较大的N,这样有
利于较大限度地平滑由随机性所带来的严重偏差;
当数据的随机因素较小时,宜选用较小的N,这有利 于跟踪数据的变化,并且预测值滞后的期数也少。
(1)一次指数平滑法的初值的确定有几种方法: 取第一期的实际值为初值; 取最初几期的平均值为初值。
一次指数平滑法比较简单,但也有问题。问题之 一便是力图找到最佳的 α 值,以使均方差最小,这需 要通过反复试验确定。
例:用一次指数平滑法对1981年1月我国平板玻璃月产量进行预
测(α=0.3,0.5 ,0.7)。并选择使均方误差最小的α进行预测
0.7 259 .5 0.3 240 .1 253 .68
几何平均法、移动平均法、指数平滑法预测

•平均预测法原理
-随机因素对数据的影响,通过对数据的平均或平滑消除后,呈现出事物的本质规律
•算术平均
-简单平均、加权平均、几何平均
几何平均
•概念:几何平均数是一个统计的概念,某一变量的几何平均值定义为:
移动平均法
原理:
通过对历史数据的移动平均,消除随机因素影响,建立模型,进而预测。
一次移动平均法、二次移动平均法
一次移动平均法
指数平滑法
•移动平均法存在着以下不足:
-丢失历史数据。
对历史数据平等对待。
•方法
-一次指数平滑法。
二次指数平滑法。
一次指数平滑法PPT课件

家庭每天的开支、一个工人的每天的工作量、一个学生 每天的伙食费,等等,也可以构成时间序列。事实上, 万事万物的变化发展所表现出来的各种特征,只要能够 被持续的观察和度量,同时被记录,就能够得到所谓的 时间序列。
时间序列与一般的统计数据的不同之处在于:这是
一些有严格先后顺序的数据。不同时间点或时间段对应 的数据之间可能是没有关联互相独立的,但大多数情况 下它们之间往往存在着某种前后相承的关系,而非互相 独立。因此,对这类数据的分析和研究需要一些特殊的 方法。时间序列分析就是包含了针对这种独特数据特点 而形成和发展起来的一系列统计分析方法的一个完整的 体系。
是不可能的。因此这种平稳性一般被称为“严平稳”或
者“完全平稳”。
●白噪声序列 白噪声序列是一种特殊的平稳序列。它定义为:若随机序列{yt}
由互不相关的随机变量构成,即对所有 st,C ovys,yt0,则称
其为白噪声序列。可以看出,白噪声序列是一种平稳序列,在 不同时点上的随机变量的协方差为0。该特性通常被称为“无 记忆性”,意味着人们无法根据其过去的特点推测其未来的走 向,其变化没有规律可循。虽然有这个特点,但白噪声序列却 是其他时间序列得以产生的基石,这在时间序列的ARIMA模 型分析中体现得相当明显。另外,时间序列分析当中,当模型 的残差序列成为白噪声序列时,可认为模型达到了较好的效果, 剩余残差中已经没有可以识别的信息。因此,白噪声数列对模 型检验也是很有用处的。
数据期间的选取也是时间序列分析中经常遇到的问 题。所谓数据期间的选取是指,如果分析过程中只希望 选取全部样本期中的部分时段数据进行分析,则应首先 指定该时间段的起止时间。对此可通过SPSS的样本选 取(Select Cases)功能实现。
13.3指数平滑法
第4章 移动平均法和指数平滑法(3)

2
3 Lag
4
5
6
Bartlett's formula for MA(q) 95% confidence bands
4.2 平均值预测法
• 例4.3残差自相关系数的Q检验结果 • • • • • • • • LAG AC 1 2 3 4 5 6 0.5063 0.0786 -0.2986 -0.6028 -0.6426 -0.2195 PAC 0.5137 -0.2146 -0.3971 -0.5096 -0.6381 0.0669 Q 7.2093 7.3904 10.126 21.807 35.745 37.456 Prob>Q 0.0073 0.0248 0.0175 0.0002 0.0000 0.0000
练习:见书P106页表4-5(例4.4)
4.2 平均值预测法
关于二次移动平均法的小结: 该方法不是用二次移动平均值直接进行预测,而是 在二次移动的基础上,利用滞后偏差建立线性预测模 型,然后再用所得到的模型进行预测 该方法适用于平稳时间序列ST,以及存在线性变化 的趋势数据 该方法可以进行远期预测,但预测误差一般都较大, 因为at,bt实际上存在近期的局限性
练习1(见书P97表4-1):如果只知道1996年各季度 的销售额,请预测1997年的销售额? 该模型的缺点:如果时间序列有增加(减少)的趋 势,预测值会一直偏低(偏高)
4.1 朴素法
(2)朴素趋势模型:
ˆ Y Y Y Y t 1 t t t 1
练习2(见书P97表4-1):如果知道1996年和1997年 各季度的销售额,请预测1998年的销售额? (3)朴素变化率模型:
指数平滑法 原理ppt课件

给予近期资料更大权重
11
12
指数平滑法 原理
王歆 苗叶馨
1
目录
1 2 3 4
定义 公式 平滑系数α 应用
2
概念
• 指数平滑法是通过计算一系列指数平 滑值来消除不规则变动,以反映时间 序列的长期趋势的统计方法。
– 在移动平均法基础上发展起来的,对时间序列 进行修匀的方法
– 原理是任一期的指数平滑值都是本期实际观察 值与前一期指数平滑值的加权平均。
t
=α ∑(1−α)t-1y1+(1−α)tE0
i=1
E0:初始值 Et数: 实质是以前各期观测值的加权算术平均
各期观测值的系数就是其比重权数
6
权数简便
优点 Text
连续计算
跟踪反应 最新变化
7
平滑系数α
随机波动成分↓ 现象趋势的变化↑ 试算得出预测误差min
α的选取
8
短期预测
无明显波动规律
水平趋势
∧yt+1=Et=αyt+(1−α)Et-1 ∧yt+1=
∧yt=Et-1
∧yt+α(yt-∧yt)
9
指数平滑法预测的基本思想
预测
无误差 有误差
剔除
随机波动 实质变化
调整
10
对比
1
2
3
全期平均法
对过去数据全部 加以同等利用
移动平均法
指数平滑法
舍弃较远期的数据
保留过去的数据
在加权移动平均法中 给予随时间变化的权数
– 应用于:直接预测+估计预测模型的参数
3
分类
一次 (教材)
一次指数平滑
两次
市场调查 第十一章 平滑预测法
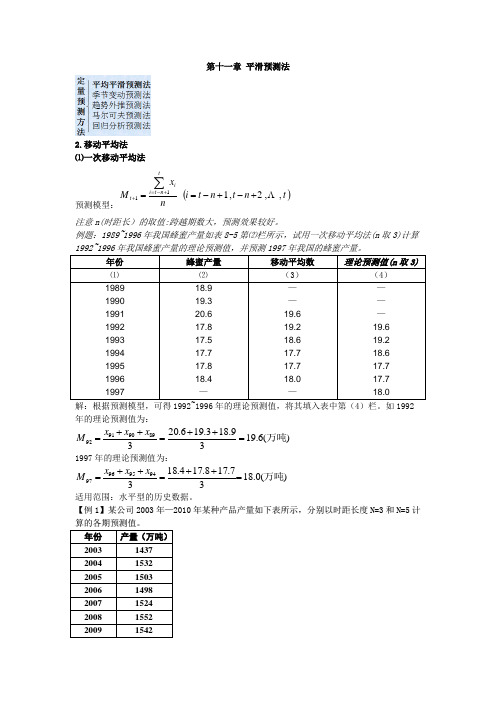
第十一章 平滑预测法2.移动平均法⑴一次移动平均法预测模型:()t n t n t i nx M tn t i it ,,2,111 +-+-==∑+-=+注意n(时距长)的取值:跨越期数大,预测效果较好。
例题:1989~1996年我国蜂蜜产量如表8-5第⑵栏所示,试用一次移动平均法(n 取3)计算1992~1996年我国蜂蜜产量的理论预测值,并预测1997年我国的蜂蜜产量。
年份 蜂蜜产量 移动平均数 理论预测值(n 取3)⑴ ⑵ (3) (4) 1989 1990 1991 1992 1993 1994 1995 1996 199718.9 19.3 20.6 17.8 17.5 17.7 17.8 18.4 —— — 19.6 19.2 18.6 17.7 17.7 18.0 —— — — 19.6 19.2 18.6 17.7 17.7 18.0解:根据预测模型,可得1992~1996年的理论预测值,将其填入表中第(4)栏。
如1992年的理论预测值为:)(6.1939.183.196.20389909192万吨=++=++=x x x M 1997年的理论预测值为:)(0.1837.178.174.183********万吨=++=++=x x x M适用范围:水平型的历史数据。
【例1】某公司2003年—2010年某种产品产量如下表所示,分别以时距长度N =3和N =5计算的各期预测值。
年份 产量(万吨)2003 1437 2004 1532 2005 1503 2006 1498 2007 1524 2008 1552 200915422010 1632 年份 产量(万吨)预测值(N=3)预测值(N=5) 2003 1437 2004 1532 2005 1503 2006 1498 2007 1524 2008 1552 2009 1542 2010 16322011年份 产量(万吨) 预测值(N=3) 预测值(N=5)2003 1437 2004 1532 2005 15032006 1498 1491 2007 1524 15112008 1552 1508 1499 2009 1542 1525 1522 2010 16321539 1524 201115751550⑵二次移动平均法预测模型:T b a Y t t T t +=+ˆ式中:T t Y +ˆ为t+T 期预测值,t 为本期,at 和 bt 为参数()t t t t t t M M M M M a ''-'=''-'+'=2()t t t M M n b ''-'-=12t M '和t M ''分别为一次移动平均数和二次移动平均数∑+-=='t n t i i t x n M 11 ∑+-==''tn t i i t M n M 11适用范围:斜坡型历史数据 例:某省1995~2004年人均卷烟消费量如表第⑵栏所示,试用二次移动平均法计算2000~2004年我国人均卷烟消费量的理论预测值,并预测2005年的卷烟消费量(时据长度=3)。
第三章 时间序列平滑法

• 计算公式:
St xt 1 St 1 bt 1
bt St St 1 1 bt 1
Ft m St bt m
第五节 二次曲线指数平滑法
• 有的时间序列虽然有增加或减少趋势,但不一定是线性的,
Ft m at bt m
m为预测超前期数
第四节 线性二次指数平滑法
一、布朗单一参数线性指数平滑法 • 其基本原理与线性二次移动平均法相似 ,因为当趋势
存在时,一次和二次平滑值都滞后于实际值,将一次 和二次平滑值之差加在一次平滑值上,则可对趋势进 行修正。
第四节 线性二次指数平滑法
二、霍尔特法相似,只是它不用
第三章 时间序列平滑预测法
第一节 一次移动平均法
第二节 一次指数平滑法
第三节 线性二次移动平均法
第四节 线性二次指数平滑法
第五节 二次曲线指数平滑法
第六节 温特线性与季节指数平滑法
第一节 一次移动平均法
一次移动平均法是收集一组观察值,计算这组观察值 的均值,利用这一均值作为下一期的预测值。 • 设时间序列为
得到预测的通式,即 :
• 一次指数平滑法是一种加权预测,权数为α。它既不需要
存储全部历史数据,也不需要存储一组数据,从而可以大 大减少数据存储问题,甚至有时只需一个最新观察值、最 新预测值和α值,就可以进行预测。它提供的预测值是前 一期预测值加上前期预测值中产生的误差的修正值。
Ft 1 xt (1 ) Ft
该公司第17期销售量的预测值为:
F17 x16 (1 ) F16 0.1 95 0.9 96.21 96.09(万元)
移动平均法and指数平滑法

移动平均法and指数平滑法感谢:⼀、移动平均法(Moving average , MA)移动平均法⼜称滑动平均法、滑动平均模型。
⽤处:⼀组最近的实际数据值->[预测]->未来⼀期或⼏期内公司产品需求量/公司产能。
分类:简单移动平均和加权移动平均思想:根据时间序列资料,逐项推移,依次计算包含⼀定项数的序时平均值,以反映长期趋势。
好处:时间序列数值受周期变动和随机波动影响起伏较⼤,不容易显⽰事件发展趋势, MA可以消除这些因素影响。
(⼀)简单移动平均法各个元素的权重相等。
公式如下:Ft=(At-1 + At-2 + At-3 + ... + At-n) / n[简单的滑动窗⼝](⼆)加权移动平均法加权移动平均给固定跨越期限内的每个变量值以不同的权重。
其原理是:历史各期产品需求的数据信息对预测未来期内的需求量的作⽤不⼀样。
Ft=w1At-1 + w2At-2 + w3At-3 + ... + wnAt-n⼆、指数平滑法(Exponential Smoothing, ES)指数平滑法认为时间序列的态势具有稳定性或规则性,所以时间序列可被合理地顺势推延;他认为最近的过去态势,在某种程度上会持续到最近的未来,所以将较⼤的权数放在最近的资料。
指数平滑法是⽣产预测中常⽤的⼀种⽅法,⽤于中短期经济发展趋势预测,所有预测⽅法中指数平滑⽤得最多。
简单的全期平均法:全部平均。
移动平均法:不考虑较远期数据,并在加权移动平均法中给予近期资料更⼤权重。
指数平滑法:兼容全期平均和移动平均所长,不舍弃过去的数据,仅给予逐渐减弱的影响程度,即随着数据的远离,赋予逐渐收敛为零的权数。
指数平滑法在移动平均法基础上发展起来的⼀种时间序列分析预测法,通过计算指数平滑值,配合⼀定的时间序列预测模型对现象的未来进⾏预测。
任⼀期的指数平滑值都是本期实际观察值与前⼀期指数平滑的加权平均。
(⼀)指数平滑法的公式S_t = a \c dot y_t + (1-a)S_{t-1}S_t:时间t的平滑值y_t: 时间t的实际值S_t-1: 时间t-1的平滑值a--平滑常数,取值范围[0, 1](⼆)指数平滑的预测公式根据平滑次数不同,指数平滑法分为:⼀次指数平滑法、⼆次指数平滑法和三次指数平滑法等(1)⼀次指数平滑y_t+1(predict) = a* y_t(actual) + (1-a) * y_t(predict)(2)⼆次指数平滑预测yt+m=(2+am/(1-a))yt'-(1+am/(1-a))yt=(2yt'-yt)+m(yt'-yt) a/(1-a)其中yt= ayt-1'+(1-a)yt-1,就是⼀次指数平滑的再平滑。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
— 203.8 209.0 230.0 226.9 223.8 211.1 209.5 219.0 212.8 219.8 233.8
α=0.7
— 203.8 211.0 224.2 223.9 221.7 205.4 207.1 222.1 211.2 222.1 240.1
回总目录 回本章目录
➢ 限制一:计算移动平均必须具有N个过
去观察值,当需要预测大量的数值时, 就必须存储大量数据;
回总目录 回本章目录
➢ 限制二:N个过去观察值中每一个权数 都相等,而早于(t-N+1)期的观察值的
权数等于0,而实际上往往是最新观察值 包含更多信息,应具有更大权重。
回总目录 回本章目录
例题分析
•例 1
式中: x t 为最新观察值;
F t 1 为下一期预测值;
由移动平均法计算公式可以看出,每 一新预测值是对前一移动平均预测值的修
正,N越大平滑效果愈好。
回总目录 回本章目录
(2)移动平均法的优点 ➢ 计算量少; ➢ 移动平均线能较好地反映时间序列 的趋势及其变化。
回总目录 回本章目录
(3)移动平均法的两个主要限制
Stxtxt1xt N 2...xtN1
StStSt 1StN 2...StN 1
(5.1) (5.2)
at 2StSt
bt N21StSt
(5.3) (5.4)
Ftmat btm m为预测超前期数
回总目录 回本章目录
其中:
分析预测我国平板玻璃月产量。
下表是我国1980-1981年平板玻璃月产量,试选用N=3 和N=5用一次移动平均法进行预测。计算结果列入表中。
时间 序号 实际观测值 三个月移动平均值 五个月移动平均值
1980.1
1
1980.2
2
1980.3
3
1980.4
4
1980.5
5
1980.6
6
1980.7
7
1980.8
α。它既不需要存储全部历史数据,也不需要
存储一组数据,从而可以大大减少数据存储问 题,甚至有时只需一个最新观察值、最新预测
值和α值,就可以进行预测。它提供的预测值
是前一期预测值加上前期预测值中产生的误差 的修正值。
回总目录 回本章目录
一次指数平滑法的初值的确定有几种方法:
➢ 取第一期的实际值为初值; ➢ 取最初几期的平均值为初值。
一次指数平滑法比较简单,但也有问题。
问题之一便是力图找到最佳的α值,以使均
方差最小,这需要通过反复试验确定。
回总目录 回本章目录ቤተ መጻሕፍቲ ባይዱ
•例2 利用下表数据运用一次指数平滑法对1981年1
月我国平板玻璃月产量进行预测(取α=0.3,0.5 , 0.7)。并计算均方误差选择使其最小的α进行预
测。
拟选用α=0.3,α=0.5,α=0.7试预测。
计算这组观察值的均值,利用这一均值 作为下一期的预测值。
回总目录 回本章目录
• 在移动平均值的计算中包括的过去观察值 的实际个数,必须一开始就明确规定。每 出现一个新观察值,就要从移动平均中减 去一个最早观察值,再加上一个最新观察 值,计算移动平均值,这一新的移动平均 值就作为下一期的预测值。
回总目录 回本章目录
实际观测值
203.8 214.1 229.9 223.7 220.7 198.4 207.8 228.5 206.5 226.8 247.8 259.5
α=0.3
— 203.8 206.9 213.8 216.8 218.0 212.1 210.8 216.1 213.2 217.3 226.5
指数平滑法
5 时间序列平滑预测法
5.1 一次移动平均法和一次指数平滑法 5.2 线性二次移动平均法 5.3 线性二次指数平滑法 5.4 布朗二次多项式(三次)指数平滑法 5.5 温特线性和季节性指数平滑法
回总目录
5.1 一次移动平均法和一次指数平滑法
一、一次移动平均法 • 一次移动平均方法是收集一组观察值,
5.2 线性二次移动平均法
一、线性二次移动平均法 (1)基本原理 为了避免利用移动平均法预测有趋势 的数据时产生系统误差,发展了线性二次 移动平均法。这种方法的基础是计算二次 移动平均,即在对实际值进行一次移动平 均的基础上,再进行一次移动平均。
回总目录 回本章目录
(2)计算方法 线性二次移动平均法的通式为:
(1)移动平均法有两种极端情况 • 在移动平均值的计算中包括的过去观察值 的实际个数N=1,这时利用最新的观察值 作为下一期的预测值; • N=n,这时利用全部n个观察值的算术平 均值作为预测值。
回总目录 回本章目录
设时间序列为 x1, x 2 , . . . , 移动平均法可以表示为: F t 1xtxt 1...xtN 1/NN 1tN t 1xi
由上表可见:
α=0.3,α=0.5,α=0.7时,均方误差分别为: MSE=287.1 MSE=297.43 MSE=233.36 最小 因此可选α=0.7作为预测时的平滑常数。
1981年1月的平板玻璃月产量的预测值为:
0 .7 2.5 5 0 .3 9 2.1 4 20 .6 58 3
回总目录 回本章目录
218.4 217.4 216.1 215.8 212.4 213.6 223.5
回总目录 回本章目录
二、一次指数平滑法 一次指数平滑法是利用前一期的预测值 F t
代替 x t n 得到预测的通式,即 :
F t1xt (1)F t
回总目录 回本章目录
由一次指数平滑法的通式可见: 一次指数平滑法是一种加权预测,权数为
结果列入下表:
回总目录 回本章目录
时间
1980.01 1980.02 1980.03 1980.04 1980.05 1980.06 1980.07 1980.08 1980.09 1980.10 1980.11 1980.12 1981.01
序号
1 2 3 4 5 6 7 8 9 10 11 12
8
1980.9
9
1980.10 10
1980.11 11
1980.12 12
203.8 214.1 229.9 223.7 220.7 198.4 207.8 228.5 206.5 226.8 247.8 259.5
215.9 222.6 224.8 214.6 209.0 211.6 214.3 220.6 227.0
