中考数学第1轮同步演练夯实基础第2部分图形与空间第7章图形与变换第25节投影与视图课件
中考数学第一轮复习精品讲解第七单元几何变化、视图与投影(共78张PPT)

图33-2
·新课标
第33讲 │ 归类示例
[解析] 轴对称图形对应角相等,对应边相等,对应线段 的连线被对称轴垂直平分,故A、C、D正确,B不正确,这 两条线段所在的直线相交于对称轴.
不管是中心对称图形还是轴对称图形,它们进行变换之后对应线 段相等,对应角也相等.
·新课标
第33讲 │ 归类示例
类型之三 镜子成像与轴对称变换
·新课标
第33讲 │ 归类示例
类型之四 轴对称与中心对称有关的作图问题
命题角度: 1.利用轴对称的性质作图 2.利用中心对称的性质作图 3.利用轴对称或中心对称的性质设计图案 [2011· 绍兴] 分别按下列要求解答: (1)在图 33-4①中,作出⊙O 关于直线 l 成轴对称的图形; (2)在图②中,作出△ABC 关于点 P 成中心对称的图形.
11.[2010· 徐州]如图34-9,在6×4方格纸中,格点三角形甲经过 旋转后得到格点三角形乙,则其旋转中心是( B ) A.点M B.格点N C.格点P D.格点Q
·新课标
第34讲 │ 考点随堂练
5.[2010· 凉山]下列图案中,只要用其中一部分平移一次就可以得 到的是( B )
A
B 图34-4
C
D
[解析] 选项A中需要通过一次平移和一次旋转才能得到; 选项C中需要平移和旋转才能得到;选项D中需要3次平移 才能得到;只有B只用一次平移即可得到.
·新课标
第34讲 │ 考点随堂练
C
D
[解析] 我们知道平移不改变图形的形状与大小,所以选项 B可排除掉,平移时,只能是沿着一条直线移动,不可以 是曲线路径,所以选项C、D即可排除掉.
·新课标
第34讲 │ 考点随堂练
中考数学一轮复习 第二讲 空间与图形 第七章 图形变换 7.2 视图、投影、尺规作图课件

考点扫描
考点1 考点2 考点3 考点4 考点5
特别提醒 在画三视图时,要注意:看不见的轮廓线要画成虚线,看得见的轮廓线要画成实线.
考点扫描
3.常见几何体的三视图
几何体
图形
长方体
圆柱
圆锥
棱锥
棱柱
球
主视图
考点1 考点2 考点3 考点4 考点5
左视图
俯视图
考点扫描
典例2 如图所示的几何体,其俯视图是 (
考点扫描
考点1 考点2 考点3 考点4 考点5
提分训练 1.( 2018·辽宁阜新 )如图所示,是一个空心正方体,它的左视图是 ( C)
【解析】由左视图的定义可知C选项正确.
考点扫描
2.( 2018·河北 )图中三视图对应的几何体是 ( C )
考点1 考点2 考点3 考点4 考点5
【解析】观察图形可知选项C符合三视图的要求.
考点扫描
考点1 考点2 考点3 考点4 考点5
投影 1.投影 一般地,用光线照射物体,在某个平面( 地面、墙壁等 )上得到的影子叫做物体的投影, 照射光线叫做投影线,投影所在的平面叫做 投影面 . 2.平行投影 有时光线是一组互相平行的射线,例如太阳光或探照灯中的光线.由平行光线形成的投 影叫做平行投影.
7.2 视图、投影、尺规作图
理解基本几何体( 直棱柱、圆柱、圆锥、球 )的三视图,会判断简单物体的三视图, 并能根据三视图描述基本几何体或实物原型,了解直棱柱、圆锥的侧面展开图,了解中 心投影与平行投影.会利用直尺与三角板作一条线段等于已知线段、作一个角等于已 知角,会作角的平分线及线段的垂直平分线.会利用基本作图作三角形,会过不在同一直 线上的三点作圆,会作三角形的外接圆、内切圆,会作圆的内接正方形和正六边形,了解 尺规作图的道理,保留作图的痕迹,不要求写出作法.
2024年江西中考数学一轮复习考点探究 投影、视图与尺规作图 学案(含答案)

第七章图形的变化第1节投影、视图与尺规作图命题分析【知识清单】知识点1 尺规作图五种基本尺规作图步骤图示作图痕迹原理适用情形作一条线段等于已知线段(已知线段a)1.作射线OP;2.以点O为圆心,a为半径作弧,交OP于点A,则OA即所求线段圆上的点到圆心的距离等于半径1.已知三边作三角形;2.作圆的内接正六边形作一个角等于已知角(已知∠α)1.以点O为圆心,适当长为半径作弧,分别交∠α的两边于点P,Q;2.作射线O'A;3.以点O'为圆心,OP长为半径作弧,交O'A于点M;4.以①为圆心;②为半径作弧,交步骤3中的弧于点N;5.过点N作射线O'B,则∠AO'B即所求角1.三边相等的两个三角形全等;2.全等三角形的对应角相等1.过直线外一点作直线与已知直线平行;2.过三角形一边上一点作直线,将其分成两个相似三角形作已知角的平分线(已知∠AOB)1.以点O为圆心,适当长为半径作弧,分别交OA,OB于点N,M;2.分别以③为圆心,以④为半径作弧,两弧在∠AOB的内部相交于点P;3.作射线OP,则OP即已知角的平分线1.三边相等的两个三角形全等;2.全等三角形的对应角相等;3.两点确定一条直线1.作一点使得该点到角两边的距离相等;2.作三角形的内切圆(续表)五种基本尺规作图步骤图示作图痕迹原理适用情形作线段的垂直平分线(已知线段AB)1.分别以⑤为圆心,以⑥为半径,在AB两侧作弧,分别交于点M,N;2.过点M,N作直线,直线MN即所求垂直平分线1.到线段两端点距离相等的点在这条线段的垂直平分线上;2.两点确定一条直线的外接圆1.过三角形的一个顶点作直线平分三角形的面积;2.过不在同一直线上的三点作圆/作三角形的外接圆;3.作到已知两点距离相等的点过一点作已知直线的垂线(已点P在直线l上1.以点P为圆心,适当长为半径作弧,交直线于A,B两点;1.到线段两端点距离相等的点在这1.已知底边上的高线及腰长作等腰三角形;知点P 和 直线l )2.分别以⑦ 为圆心,以⑧ 为半径向直线两侧作弧,两弧分别交于点M ,N ;3.过点M ,N 作直线,直线MN 即所求垂线条线段的垂直平分线上; 2.两点确定一条直线2.过直线外一点作与该直线相切的圆点P 在直线l 外1.任意取一点M ,使点M 和点P 在直线l 的两侧;2.以⑨为圆心,为半径作弧,交直线l 于A ,B 两点;3.分别以为圆心,以为半径作弧,交点M 同侧于点N ;4.过点P ,N 作直线,直线PN 即所求垂线知识点2 投影与视图投影{概念:一般地,用光线照射物体,在某个平面(如地面、墙壁等)上得到的影子叫做物体的投影,照射光线叫做投影线投影所在的平面叫做投影面分类{平行投影:由⑬ 光线形成的投影叫做平行投影,物体在太阳光照射下形成的影子可以看成平行投影正投影:投影线⑭ 于投影面产生的投影叫做正投影中心投影:由同一点(点光源)发出的光线形成的投影叫做中心投影,如灯光下某物体的投影三视图知识点3 常见几何体的三视图与展开图几何体正方体圆柱长方体圆锥球体三棱柱三视图展开图 (任一种)无【参考答案】①M ②PQ ③M ,N ④大于12MN 的长 ⑤A ,B ⑥大于12AB 的长 ⑦A ,B ⑧大于12AB 的长 ⑨P PMA ,B大于12AB 的长平行 垂直 由前向后 由左向右由上向下长对正 高平齐 宽相等 实线虚线【自我诊断】1.如图,这是由五个相同的小立方块搭成的几何体,则这个几何体的左视图是( )A BC D2.下列四幅图,表示两棵树在同一时刻阳光下的影子是( )A B C D3.某正方体的每个面上都有一个汉字,如图,这是它的一种表面展开图,那么在原正方体中,与“中”字所在面相对面上的汉字是( )A.故B.讲C.国D.事4.由几个大小相同的小正方体搭建而成的几何体的主视图和俯视图如图所示,则搭建这个几何体所需要的小正方体的个数可能为( )A.5B.6C.5或6D.6或7【参考答案】1.C2.B3.D4.C【真题精粹】考向1 投影1.(拓展)如图,位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2∶5,且三角尺的一边长为8 cm,则投影三角形的对应边长为( )A.12 cmB.20 cmC.3.2 cmD.10 cm考向2 三视图(6年4考)2.(2019·江西)如图,这是由手提水果篮抽象出的几何体,以箭头所指的方向为主视图方向,则它的俯视图为( )A B C D3.(2021·江西)如图所示的几何体的主视图是( )A B C D4.(2018·江西)如图所示的几何体的左视图为( )5.(2022·江西)如图,这是由四个完全相同的小正方体搭成的几何体,它的俯视图为( )A B C D热点预测A B C D考向3 创新作图(必考)7.(2023·江西)如图,这是4×4的正方形网格,请仅用无刻度的直尺按要求完成以下作图.(保留作图痕迹)(1)在图1中作锐角△ABC,使点C在格点上.(2)在图2中的线段AB上作点Q,使PQ最短.8.(2018·江西)如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,请仅用无刻度直尺........分别按下列要求画图.(保留画图痕迹)(1)在图1中,画出△ABD中BD边上的中线.(2)在图2中,若BA=BD,画出△ABD中AD边上的高.图1图29.(2021·江西)已知正方形ABCD的边长为4个单位长度,E是CD的中点,请仅用无刻度直尺........按下列要求作图.(保留作图痕迹)(1)在图1中,将直线AC绕着正方形ABCD的中心顺时针旋转45°.(2)在图2中,将直线AC向上平移1个单位长度.热点预测考向4 立体图形的展开图与折叠(仅2020年考查)11.(2020·江西)如图,正方体的展开图为( )【参考答案】1.B2.A3.C4.D5.A6.D7.略8.略9.略10.略11.A【核心突破】考点1投影例题1如图,树AB在路灯O的照射下形成投影AC,若树高AB=2 m,树影AC=3 m,树与路灯的水平距离AP=4.5 m,则路灯的高度OP是( )A .3 mB .4 mC .5 mD .6 m变式特训1.如图1,随着光伏发电项目投资成本下降,越来越多的“光伏”项目正在逐步走进我们的生活.光伏发电不仅能为城市提供清洁能源,还能减少城市污染和能源消耗.如图2,长BC=8 m,宽AB=1.5 m 的太阳能电池板与水平面成30°夹角,经过太阳光的正投影,它在水平面所形成的阴影的面积为( )A .12 m 2B .6 m 2C .6√3 m 2D.9√32 m 2考点2 三视图例题2(2023·鹰潭模拟) 如图,该几何体的左视图是( )A B C D变式特训2.(民族文化)江西茶文化源远流长,其历史可追溯到两千年前的秦汉时期.如图,这是江西名茶中一种装茶的罐子及抽象出的立体图形,则其主视图为( )A B C D3.(古人智慧)在我国古代建筑中经常使用榫卯构件,如图,这是某种榫卯构件的示意图,其中卯的俯视图是( )A BC D考点3立体图形的展开与折叠例题3(2023·巴中)某同学学习了正方体的表面展开图后,在如图所示的正方体的表面展开图上写下了“传承红色文化”六个字,还原成正方体后,“红”的对面是( )A.传B.承C.文D.化方法提炼变式特训4.一个骰子相对两面的点数之和为7,它的展开图如图所示,下列判断正确的是( )A.A代表B.B代表C.C代表D.B代表5.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,则下列序号中不应剪去的是( )A.3B.2C.6D.16.三棱柱的展开图不可能是( )A BC D考点4创新作图例题4(2023·鹰潭模拟) 图1,图2都是由边长为1的小等边三角形构成的网格,△ABC为格点三角形.请仅用无刻度直尺在网格中完成下列画图.(1)在图1中,画出△ABC中AB边上的中线CM.(2)在图2中,画出∠APC,使∠APC=∠ABC,且点P在格点上.(画出一个即可)变式特训7.已知四边形ABCD 为平行四边形,E 为AB 边的中点,请仅用无刻度直尺分别按下列要求作图.(保留作图痕迹) (1)在图1中,作出AD 边的中点P.(2)在图2中,在AD 边上求作一点M ,使△ABM 的面积为▱ABCD 面积的13.8.在图1,图2中,四边形ABCD 为矩形,某圆经过A ,B 两点,请你仅用无刻度直尺分别按下列要求作图.(1)在图1中画出该圆的圆心O. (2)在图2中画出线段CD 的垂直平分线.【参考答案】 例题1 C变式特训1.C例题2 B变式特训2.D3.C例题3 D变式特训4.A5.A6.D 例题4略变式特训7.略8.略。
中考数学第一部分基础知识过关第七章图形与变换第25讲投影与视图

解析 如图所示,AC的长就是蚂蚁爬行的最短距离.C,D分别是 BE,AF的中点.
∵AF=2π×5=10π,∴AD=5π.
∴AC= ≈16 cm. AD2 CD2
2021/12/13
第三十八页,共三十九页。
内容(nèiróng)总结
第25讲 投影与视图。一个圆和一个扇形。何体的上下前后,由俯视图分清几何体的左右前后.。 中考解题指导 解决此类题目(tímù)的关键是能够根据三视图判断几
2021/12/13
第三十六页,共三十九页。
解析 (1)如图,注意AC与EF平行(píngxíng).
(2)由题意,得 1 . 6=5 ,解D 得E DE=18.15米≈18.2米. 1 .1 1 2 .1
2021/12/13
第三十七页,共三十九页。
10.有一圆柱体如图,高4 cm,底面半径5 cm,A处有一蚂蚁,若蚂蚁 欲爬行到C处,求蚂蚁爬行的最短距离.(保留整数(zhěngshù))
2021/12/13
第二十九页,共三十九页。
5.下列图形中,表示两棵小树在同一(tóngyī)时刻阳光下的影子的图形可 能是 ( A )
2021/12/13
第三十页,共三十九页。
二、填空题
6.(2018东营)一个圆锥体的三视图如图所示,则这个圆锥体的侧 面积(miàn jī)为 20π .
解析 由圆锥的三视图可知,圆锥的高为3,圆锥的底面直径为8,
2021/12/13
第五页,共三十九页。
知识点二 视图 1.三视图:在正面内得到的由前向后观察物体(wùtǐ)的视图叫做⑤ 主视
图 ;在水平面内得到的由上到下观察物体的视图叫做⑥ 俯视图 ;在侧
面内得到的由左到右观察物体的视图叫做⑦ 左视图 .
2024年云南省中考数学一轮复习 第25讲 投影与视图课件

观察几何体三视图时出现错误 1.如图所示的空心圆柱,其俯视图是( D )
2.如图所示,将小立方块①从6个大小相同的小立方块所搭的几何体中 移走后,所得几何体( D ) A.俯视图不变,左视图改变 B.主视图改变,左视图改变 C.主视图不变,左视图不变 D.俯视图改变,左视图改变
由视图联想实物时辨别失误 3.如图所示的是某几何体从上面看到的平面图形,小正方形中的数字 表示该位置小正方体的个数,则从正面看到的该几何体的平面图形是 ( B)
A.合 B.同 C.心 D.人
1.三个立体图形的展开图如图所示,则相应的立体图形是( A ) A.①圆柱,②圆锥,③三棱柱 B.①圆柱,②球,③三棱柱 C.①圆柱,②圆锥,③四棱柱 D.①圆柱,②球,③四棱柱
2.把如图所示的正方体展开,得到的平面展开图可能是( B )
与视图有关的计算(命题热点) (2021云南)下列是某几何体的三视图(其中主视图也称正 视图,左视图也称侧视图).已知主视图和左视图是两个全等的矩形,若 主视图的相邻两边长分别为2和3,俯视图是直径等于2的圆,则这个几 何体的体积为 3π .
3.如图所示的是由几个大小完全相同的小正方体搭成的几何体.
(1)请分别画出该几何体的三视图;
(2)图中共有
个小正方体.
解:(1)几何体的三视图,如图所示.
(2)8
角度2 由三视图判断几何体
(2023云南)某班同学用几个几何体组合成一个装饰品美化
校园,其中 一个几何体的三视图(其中主视图也称正视图,左视图也 称侧视图)如图所示,这个几何体是( A )
搭几何体恰好和小明所搭几何体拼成一个无空隙的大长方体(不改变
小明所搭几何体的形状). (1)按照小明的要求,小亮至少需要 18 个正方体积木; (2)按照小明的要求,小亮所搭几何体的表面积最小为 46 .
2024-2025学年沪科版初中数学九年级(下)教案第25章投影与视图25.2三视图(第2课时)
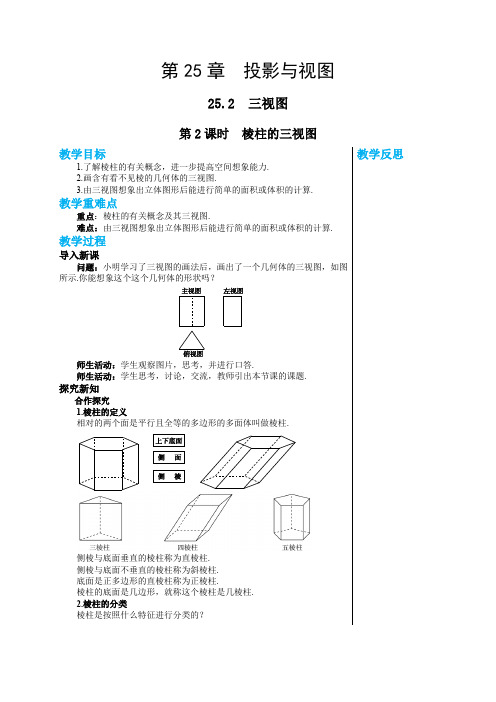
第25章投影与视图25.2 三视图第2课时棱柱的三视图教学反思教学目标1.了解棱柱的有关概念,进一步提高空间想象能力.2.画含有看不见棱的几何体的三视图.3.由三视图想象出立体图形后能进行简单的面积或体积的计算.教学重难点重点:棱柱的有关概念及其三视图.难点:由三视图想象出立体图形后能进行简单的面积或体积的计算.教学过程导入新课问题:小明学习了三视图的画法后,画出了一个几何体的三视图,如图所示.你能想象这个这个几何体的形状吗?师生活动:学生观察图片,思考,并进行口答.师生活动:学生思考,讨论,交流,教师引出本节课的课题.探究新知合作探究1.棱柱的定义相对的两个面是平行且全等的多边形的多面体叫做棱柱.侧棱与底面垂直的棱柱称为直棱柱.侧棱与底面不垂直的棱柱称为斜棱柱.底面是正多边形的直棱柱称为正棱柱.棱柱的底面是几边形,就称这个棱柱是几棱柱.2.棱柱的分类棱柱是按照什么特征进行分类的?例1 根据物体的三视图,描述物体的形状.【分析】由主视图可知,物体的正面是正五边形;由俯视图可知,由上向下看到物体有两个面的视图是矩形,它们的交线是一条棱(中间的实线表示),可见到,另有两条棱(虚线表示)被遮挡;由左视图可知,物体左侧有两个面是矩形,它们的交线是一条棱(中间的实线表示),可见到.综合各视图可知,物体的形状是正五棱柱.【归纳总结】虑整体图形.3.三视图的有关计算例2 按照三视图确定制作每个密封罐所需钢板的面积 (图中尺寸单位:师生活动:的侧面展开图,然后进行面积的计算.【解】由三视图可知,密封罐的形状是正六棱柱.密封罐的高为50 mm ,底面正六边形的直径为如图,是它的展开图.由展开图可知,制作一个密封罐所需钢板的面积为6×50×50+2×6×12×50×50sin 60°=6×502×1⎛ ⎝≈27 990(mm 2).教学反思【归纳总结】1.三种图形的转化:.↔↔三视图立体图展开图2. 由三视图求立体图形的面积的方法:(1) 先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高. (2) 将立体图形展开成一个平面图形 (展开图),观察它的组成部分. (3) 最后根据已知数据,求出展开图的面积.【新知应用】例3 如图是一个几何体的三视图,根据所标数据,求该几何体的表面 积和体积.师生活动:学生根据求立体图形面积的方法,独立解决,并展示.教师根据学生展示情况进行讲解:由三视图可知该几何体是由圆柱、长方体组合而成.分别计算它们的表面积和体积,然后相加即可.【解】该图形上、下部分分别是圆柱、长方体,根据图中数据得: 表面积为20×32π+30×40×2+25×40×2+25×30×2=(5 900+640π)(cm 2),体积为25×30×40+102×32π=(30 000+3 200π)(cm 3).课堂练习1.( )第1题图A.四棱锥B.四棱柱C.三棱锥D.三棱柱2. 一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为( )教学反思第2 A. 6B. 8C. 12D. 24 3. 一个物体的俯视图是圆,则该物体有可能是_______.4. 在一仓库里堆放着若干相同的正方体货箱,仓库管理员将这堆货箱的三视图画了出来.箱.第4题图5. 如图是一个由若干个棱长为1 cm 的正方体构成的几何体的三视图. (1) 请写出构成这个几何体的正方体的个数为_______; (2) 计算这个几何体的表面积为_______.第5题图6. (1) 一个几何体的主视图和左视图如图所示,请补画这个几何体的俯视图.第6(2) 一个直棱柱的主视图和俯视图如图所示.描述这个直棱柱的形状,并补画它的左视图.第6题图(2)教学反思7.如图是一个几何体的三视图,试描述这个零件的形状,并求出此三视第7题图参考答案1.D2.B3.圆柱,球4.95.(1)5 (2)20 cm 26.解:(1第6题答图(1)(2第6题答图(2)7.解:由三视图知该几何体是一个组合体,上面是一个圆锥,下面是一个圆柱.该几何体的表面积为π×22+2π×2×2+π×2×4=20 π.课堂小结学生先自主回顾本节课所学主要内容,然后师生共同总结.布置作业教材第89页复习题B 组1~2题板书设计25.2 三视图 第2课时 棱柱的三视图教学反思2.三视图的有关计算教学反思(1)三种图形的转化:三视图立体图展开图.(2)由三视图求立体图形的面积的方法:①先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高.②将立体图形展开成一个平面图形(展开图),观察它的组成部分.③最后根据已知数据,求出展开图的面积.。
2024年中考数学一轮复习考点精讲课件—投影与视图

2)由物体的三视图想象几何体的形状是有一定难度的,可以从以下途径进行分析:
① 根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,以及几何体的长、宽、高;
② 从实线和虚线想象几何体看得见部分和看不见部分的轮廓线;
③ 熟记一些简单的几何体的三视图对复杂几何体的想象会有帮助.
考点一 图形的投影
3)立体图形的正投影
物体的正投影的形状、大小与物体相对于投影面的位置有关,立体图形的正投影与平行于投影面且过立体图形的最
大截面全等.
投影的判断方法:
1)判断投影是否为平行投影的方法是看光线是否是平行的,如果光线是平行的,那么所得到的投影就是平行投影.
2)判断投影是否为中心投影的方法是看光线是否相交于一点,如果光线是相交于一点的,那么所得到的投影就是中
【例2】(2021·安徽淮南·校联考模拟预测)下列现象中,属于中心投影的是(
A.白天旗杆的影子
B.阳光下广告牌的影子
C.灯光下演员的影子
D.中午小明跑步的影子
)
考点一 图形的投影
题型03 正投影
【例3】(2022·浙江温州·温州绣山中学校联考二模)由四个相同小立方体拼成的几何体如图所示,当光线由上向
1 ) 等 高 的 物 体 垂 直 地 面 放 置 时 ( 图 1 ) , 在 太 阳 光 下 , 它 们 的 影 子 一 样 长 .
2)等长的物体平行于地面放置时(图2),它们在太阳光下的影子一样长,且影长等于物体本身的长度.
图1
图2
【小技巧】
1)图1中,两个物体及它们各自的影子及光线构成的两个直角三角形相似,相似三角形对应边成比例.
【变式8-1】(2021·宁夏吴忠·统考模拟预测)一个几何体的三视图如图所示,则该几何体的表面积为 3π+4 .
中考数学一练通 第一部分 基础考点巩固 第七章 视图与变换 7.2 视图与投影课件

1.如图,夜晚路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子
( )B
A.越长 12/10/2021
B.越短
C.一样长
D.随时间变化而变化
第二页,共十二页。
考点(kǎo 2 diǎn) 视图
陕西考点(kǎo diǎn) 解读
中考说明:会画直棱柱、圆柱、圆锥、球的主视图、左视图、俯视图,能判断简单物体的视图, 并会根据视图描述简单的几何体。
12/10/2021
第八页,共十二页。
重难突破(tūpò)强 化 重难点1 简单(jiǎndān)组合体的三视图(重点)
例1 如图的几何体的主视图正确的是( )D
【解析】从正面看,该几何体的主视图是由一个矩形和一个三角形组成的。故选D。 例2 如图是由正方体和圆锥组成的几何体,它的俯视图是( ) D
主视图:在正面内得到的由前向后观察物体的视图,叫作主视图。(3)俯视图:在水平面内得到的由上向下观察物体的视图,叫作俯视图。A
12/10/2021
第十二页,共十二页。
12/10/2021
第十页,共十二页。
重难突破(tūpò)强 化
重难点2 几何体的表面展开(zhǎn kāi)图(重点)
例5 下列四个图形,是三棱锥的表面展开图的是( )
A
【解析】A.折起来得到一个三棱锥;B.折起来是一个无底的四棱锥;C.折起来是一个三 棱柱;D.折起来是一个四棱锥。故选A。
12/10/2021
图是( )
B
12/10/2021
第六页,共十二页。
陕西考点(kǎo diǎn) 解读
考点3 立体图形(túxíng)的展开与折叠
1.常见立体图形的表面展开图 (1)棱柱的表面展开图是两个完全相同的多边形(底面)和几个矩形(侧面)。 (2)棱锥的表面展开图是一个多边形(底面)和几个三角形(侧面)。 (3)圆柱的表面展开图是两个圆(底面)和一个矩形(侧面)。 (4)圆锥的表面展开图是一个圆(底面)和一个扇形(侧面)。 2.正方体的表面展开图 第一类(“一四一”型):中间四个面,上、下各一面。
