2017年“大梦杯”福建省初中数学竞赛试题参考答案
2018年“大梦杯”福建省初中数学竞赛试题参考答案
2018年“大梦杯”福建省初中数学竞赛试题参考答案及评分标准一、选择题(共5小题,每小题7分,共35分)01.若关于x 的方程244310x mx m +--=有两个相等的实数根,则32442m m m ++-的值为( A )A .3-B .2-C .1-D .1【解答】依题意,21616(31)0m m D =++=,∴2310m m ++=,∴231m m =--,231m m +=-。
∴3222442(31)44232123m m m m m m m m m ++-=--++-=+-=--=-。
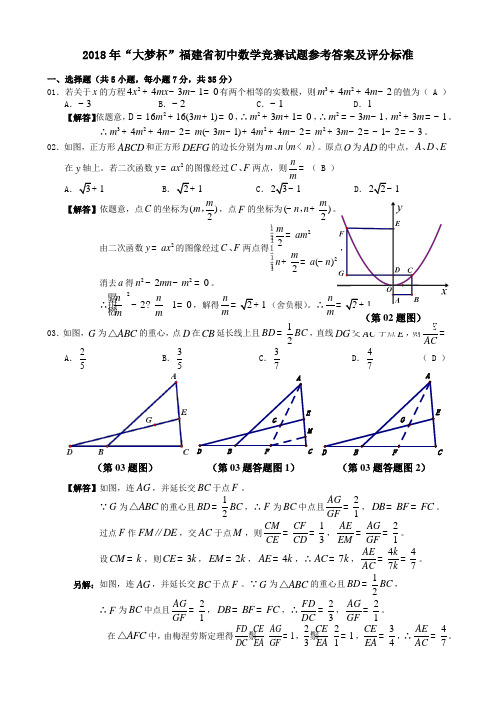
02.如图,正方形ABCD 和正方形DEFG 的边长分别为()m n m n <、。
原点O 为AD 的中点,A D E 、、在y 轴上。
若二次函数2y ax =的图像经过C F 、两点,则nm=( B ) A .31+ B .21+ C .231- D .221-【解答】依题意,点C 的坐标为()2m m ,,点F 的坐标为()2mn n -+,。
由二次函数2y ax =的图像经过C F 、两点得222()2mam m n a n ì=ïïíï+=-ïî,消去a 得2220n mn m --=。
∴2210n n m m骣-?=琪桫,解得21n m =+(舍负根)。
∴21n m =+。
03.如图,G 为ABC △的重心,点D 在CB 延长线上且12BD BC =,直线DG 交AC 于点E ,则AEAC=A .25B .35C .37D .47( D )ME GFB DEGFB【解答】如图,连AG ,并延长交BC 于点F 。
∵G 为ABC △的重心且12BD BC =,∴F 为BC 中点且21AG GF =,DB BF FC ==。
过点F 作FM DE ∥,交AC 于点M ,则13CM CF CE CD ==,21AE AG EM GF ==。
2019年“大梦杯”福建省初中数学竞赛试题参考答案(PDF版)

2019年“大梦杯”福建省初中数学竞赛试题参考答案考试时间2019年3月17日9∶00-11∶00满分150分一、选择题(共5小题,每小题7分,共35分)。
每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。
请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.若一次函数2y x =+与反比例函数4y x=的图像交于11()A x y ,,22()B x y ,两点,则1212x x y y +的值为()A .8B .6C .6-D .8-【答案】D【解答】由24y x y x =+⎧⎪⎨=⎪⎩,得2240x x +-=……………①。
依题意,1x ,2x 是方程①的两根,于是122x x +=-,124x x =-。
∴121212121212441616484x x y y x x x x x x x x +=+⋅=+=-+=--。
2.如图,ABC △为圆O 的内接三角形,D 为BC 中点,E 为OA 中点,40ABC ∠=︒,80BCA ∠=︒,则OED ∠的大小为()A .15︒B .18︒C .20︒D .22︒【答案】C【解答】如图,连结OC 。
由40ABC ∠=︒,80BCA ∠=︒,得60BAC ∠=︒。
∵D 为BC 中点,∴OD BC ⊥,1602DOC BOC BAC ∠=∠=∠=︒。
∴30OCD ∠=︒,12OD OC =。
又E 为OA 中点,∴12OE OA OD ==。
结合40ABC ∠=︒,知24060140EOD AOC COD ∠=∠+∠=⨯︒+︒=︒,(第2题图)(第2题答题图)11(180)(180140)2022OED EOD ∠=︒-∠=︒-︒=︒。
3.已知二次函数2()2f x x ax b =++,若()(1)f a f b =+,其中1a b ≠+,则(1)(2)f f +的值为()A .8B .10C .12D .14【答案】A【解答】由已知条件及二次函数图像的对称性,知124a b a ++=-。
2017年全国初中数学联合竞赛(初二年级)试题参考答案及

在 Rt △ EAD 中,有 422 (98 x)2 x2 ,解得 x 58 .
2017 年全国初中数学联合竞赛试题(初二年级)参考答案及评分标准 第 2 页(共 5 页)
二、填空题:(本题满分 28 分,每小题 7 分)
1.使得等式 1 1 a 3 a 成立的实数 a 的值为_______. 【答】 8 . 由所给等式可得 (1 1 a)3 a2 .令 x 1 a ,则 x 0 ,且 a x2 1,于是有 (1 x)3 (x2 1)2 ,
4.已知正整数 a,b, c 满足 a2 6b 3c 9 0 , 6a b2 c 0 ,则 a2 b2 c2 = ( )
A. 424. 【答】C.
B. 430.
C. 441.
D. 460.
由已知等式消去 c 整理得 (a 9)2 3(b 1)2 75 ,所以 3(b 1)2 75 ,又 b 为正整数,解得1 b 6 .
2
2
Байду номын сангаас
3
A
D
F
所以梯形的面积为 1 (1 4) 4 2 10 2 .
2
3
3
E
6.如图,梯形 ABCD 中, AD // BC , A 90 ,点 E 在 AB 上,若 AE 42 ,
BE 28, BC 70 , DCE 45 ,则 DE =
()
B
C
A. 56.
B. 58.
C.60.
D. 62.
为 A. 4. 【答】B.
B.3.
C.2.
D.1.
()
若 (a,b, c) 为好数组,则 abc 2(a b c) 6c ,所以 ab 6 .显然, a 只能为 1 或 2.
2018年“大梦杯”福建省初中数学竞赛试题+参考答案与评分标准-(12005)
2018年“大梦杯”福建省初中数学竞赛试题 考试时间 2018年3月18日 9∶00-11∶00 满分150分一、选择题(共5小题,每小题7分,共35分)。
每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。
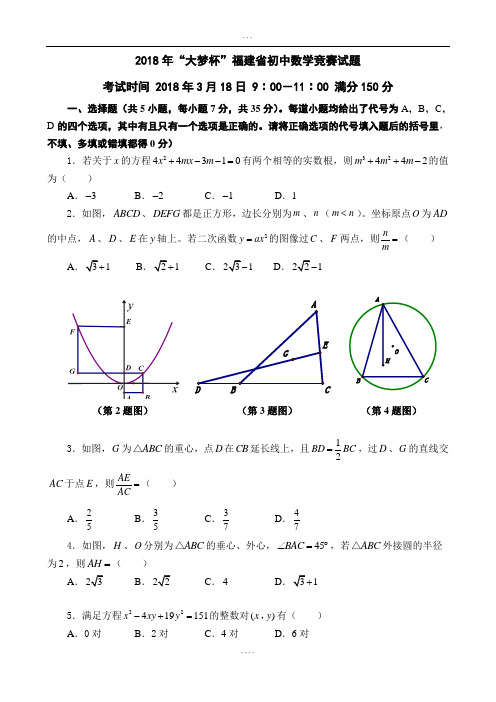
请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.若关于x 的方程244310x mx m +--=有两个相等的实数根,则32442m m m ++-的值为( )A .3-B .2-C .1-D .12.如图,ABCD 、DEFG 都是正方形,边长分别为m 、n (m n <)。
坐标原点O 为AD 的中点,A 、D 、E 在y 轴上。
若二次函数2y ax =的图像过C 、F 两点,则nm=( ) A.1 B1 C.1 D.13.如图,G 为ABC △的重心,点D 在CB 延长线上,且12BD BC =,过D 、G 的直线交AC 于点E ,则AEAC=( ) A .25B .35C .37D .474.如图,H 、O 分别为ABC △的垂心、外心,45BAC ∠=︒,若ABC △外接圆的半径 为2,则AH =( )A. B. C .4 D15.满足方程22419151x xy y -+=的整数对()x y ,有( ) A .0对 B .2对 C .4对D .6对(第4题图)(第2题图)(第3题图)6.已知a ,b ,c 为正整数,且a b c >>。
若b c +,a c +,a b +是三个连续正整数的平方,则222a b c ++的最小值为 。
7.如图,ABCD 为矩形,E 为对角线AC 的中点,A 、B 在x 轴上。
若函数4y x=(0x >)的图像过D 、E 两点,则矩形ABCD 的面积为 。
8.如图,ABC △是边长为8的正三角形,D 为AB 边上一点,1O ⊙为ACD △的内切圆,2O ⊙为CDB △的边DB 上的旁切圆。
全国初中数学竞赛试题(福建)及参考答案

全国初中数学竞赛试题(福建)及参考答案一、选择题(共5小题,每小题6分,满分30分,以下每道小题均给出了代号为A 、B 、C 、D 的四个选项,期中有且只有一个选项是正确的,请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1、已知实数x ,y 满足42423x x -=,423y y +=,则444y x+的值为( )。
A 、7B 、12 C 、72 D 、5 [答]A解:因为2x >0,2y ≥0,由已知条件得21x ==,2y ==, 所以 444y x +=2222223367y y x x++-=-+= 2、把一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷2次,若两个正面朝上的编号分别为m ,n ,则二次函数2y x mx n =++的图象与x 轴有两个不同交点的概率是( )。
A 、512 B 、49 C 、1736D 、12 [答]C解:基本事件总数有6×6=36,即可以得到36个二次函数,由题意知 △=24m n ->0,即24m n通过枚举知,满足条件的m ,n 有17对,故1736p =3、有两个同心圆,大圆周上有4个不同的点,小圆周上有2个不同的点,则这6个点可以确定的不同直线最少有( )。
A 、6条B 、8条C 、10条D 、12条[答]B解:如图,大圆周上有4个不同的点 A 、B 、C 、D ,两两连线可以确定6条不同的直线;小圆周上的两个点E 、F 中,至少有一个不是四边形ABCD 的对角线AC 与 BD 的交点,则它与A ,B ,C ,D 的连线中,至少有两条不同于A ,B ,C ,D 的两两连线,从而这6个点可以确定的直线不少于8条。
当这6个点如图所示放置时,恰好可以确定8条直线,所以,满足条件的6个点可以确定的直线最少有8条。
4、已知AB 是半径为1的圆O 的一条弦,且AB =a <1,以AB 为一边在圆O 内作正△ABC ,点D 为圆O 上不同于点A 的一点,且DB =AB =a ,DC 的延长线交圆O 于点E ,则AE 的长为( )。
2017初中数学联合竞赛省初赛试题解答及评分标准(八年)

)
B
D E
C
2 SADC CD AF 7 12 28 法可得 CE . AD AD 15 5 1 1 6.已知 a = 5 , 那么代数式 a 最大值与最小值之差等于 a a
A. 2. B. 4.
1
( B )
C. 6.
D.8.
解析
欲使代数式
1 a 取到最大值,则 a 0 , 于是 a
(15 分)
(18 分) (20 分) (5 分)
a 2b b2c c2a ab2 bc2 ca 2 (a b)(b c)(c a) 0 .
(a 1)(b 1) (b 1)(c 1) (c 1)(a 1)=k 1 ,
令 ab a b bc b c ac c a =k , 则 因此 [(a 1)(b 1)(c 1)] (k 1) ,
4.设 a,b 是实数,若 a b 2 a 1 4 b 1 5 ,则 a b 的值等于 A. 3 . 解析
a b 2 a 1 4 b 1 5 ( a 1 1)2 ( b 1 2)2 0
a 2 , b 3 a b 1. 5 . 如 图 , 在 △ ABC 中 , AB=13,BC 21, CA 20 . D 是 BC 上 一 点 , 满 足
1 1 1 . 3 1 7 1 7
解析
1 1 1 7 1 7 1 7 1 7 1
7
1 1
7 1
7
. 7 3
1
A
8. 如图, ABC 、 CDE 均为等边三角形, 且 A, D, E 三 点共线, 点 D 在 A, E 之间, BDE 30 . 则 解析
历届“大梦杯”福建省初中数学竞赛试题及答案
由条件易得 △ACE ∽△BAE ,
(第 9 题)
∴ CE AE , AE2 CE EB ,即 AE2 mEB 。 AE BE
结合 AB2 AE2 EB2 ,得 (2 5m)2 mEB EB2 。 (或由射影定理得 BA2 BE BC ,即 (2 5m)2 BE (BE m) ) ∴ EB2 mEB 20m2 0 ,解得 EB 4m 或 EB 5m(舍去)。
将 t 4 代入方程①,解得 x2 8 ,x 2 6 ;t 4 代入方程①,解得 x2 8 ,x 2 10 。
3
3
3
5
5
5
∴ xy 的最大值为 4 ,最小值为 4 。
3
5
因此, M 8 4 20 , m 8 4 12 , M m 20 12 136 。
3
3
5
y 10 ,或 x 2 10 , y 10 时等号成立。
5
5
5
∴ xy 的最小值为 4 , u x2 xy 4y2 2xy 4 的最小值为 12 ,即 m 12 。
5
5
5
∵ 3xy 4xy (x2 4 y2 4) 4 (x 2y)2 4,当且仅当 x 2y ,即 x 2 6 ,y 6 或
不填、多填或错填都得 0 分)
1.在平面直角坐标系 xOy 中,已知点 B(0,2) ,点 A 在 x 轴正半轴上且 BAO 30 。将
△OAB 沿直线 AB 折叠得 △CAB ,则点 C 的坐标为( )
A. (1, 3)
B. ( 3 ,3)
C. (3, 3) D. ( 3 ,1)
2.若实数 a , b 满足 a2 3a 2 , b2 3b 2 ,且 a b ,则 (1 a2 )(1 b2 ) ( )
2017-2018学年福建省八年级(上)竞赛数学试卷及答案与解析
2017-2018学年福建省八年级(上)竞赛数学试卷;一、选择题(每小题5分,共40分)1.下列四组数据中,不能作为直角三角形的三边长的是()A.7,24,25 B.6,8,10 C.9,12,15 D.3,4,62.设M=(x﹣3)(x﹣7),N=(x﹣2)(x﹣8),则M与N的关系为()A.M<N B.M>N C.M=N D.不能确定3.观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187…,解答下列问题:3+32+33+…+32015的末位数字是()A.1 B.3 C.7 D.94.若实数x、y、z满足(x﹣z)2﹣4(x﹣y)(y﹣z)=0,则下列式子一定成立的是()A.x+y+z=0 B.x+y﹣2z=0 C.y+z﹣2x=0 D.z+x﹣2y=05.已知△ABC中,AB=AC,高BD、CE交于点O,连接AO,则图中全等三角形的对数为()A.3 B.4 C.5 D.66.如图,在△ABC中,∠C=90°,∠BAC=30°,AB=8,AD平分∠BAC,点PQ分别是AB、AD边上的动点,则PQ+BQ的最小值是()A.4 B.5 C.6 D.77.点P(3,﹣5)关于y轴对称的点的坐标为()A.(﹣3,﹣5)B.(5,3) C.(﹣3,5)D.(3,5)8.下列四个命题中,真命题有()①两条直线被第三条直线所截,内错角相等.②如果∠1和∠2是对顶角,那么∠1=∠2.③三角形的一个外角大于任何一个内角.④如果x2>0,那么x>0.A.1个 B.2个 C.3个 D.4个二、填空题(每小题5分,共40分);9.若2a3x b y+5与5a2﹣4y b2x是同类项,则xy=.10.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的度数为.11.如果(a2+b2+2)(a2+b2﹣2)=45,则a2+b2的值为.12.已知(a+25)2=1000,则(a+15)(a+35)的值为.13.计算(1﹣)()﹣(1﹣﹣)()的结果是.14.如图,在△ABC中,I是三内角平分线的交点,∠BIC=130°,则∠A=.15.如图钢架中,焊上等长的13根钢条来加固钢架,若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是.16.如图,AB=AC,则数轴上点C所表示的数为.三、解答题(每小题10分,共40分)17.已知:3a=2,3b=6,3c=18,试确定a、b、c之间的数量关系.18.已知a=2015x+2014,b=2015x+2015,c=2015x+2016.求a2+b2+c2﹣ab﹣bc﹣ca的值.19.如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.(1)当∠BQD=30°时,求AP的长;(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.20.已知△ABC中,∠A:∠B:∠C=3:4:2,AD、BE是角平分线.求证:AB+BD=AE+BE.2017-2018学年福建省八年级(上)竞赛数学试卷参考答案与试题解析一、选择题(每小题5分,共40分)1.下列四组数据中,不能作为直角三角形的三边长的是()A.7,24,25 B.6,8,10 C.9,12,15 D.3,4,6【考点】勾股数.【分析】根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形.如果没有这种关系,这个就不是直角三角形.【解答】解:A、72+242=252,符合勾股定理的逆定理,故能作为直角三角形的三边长;B、62+82=102,符合勾股定理的逆定理,故能作为直角三角形的三边长;C、92+122=152,符合勾股定理的逆定理,故能作为直角三角形的三边长;D、32+42≠62,不符合勾股定理的逆定理,故不能作为直角三角形的三边长.故选D.2.设M=(x﹣3)(x﹣7),N=(x﹣2)(x﹣8),则M与N的关系为()A.M<N B.M>N C.M=N D.不能确定【考点】多项式乘多项式.【分析】根据多项式乘多项式的运算法则进行计算,比较即可得到答案.【解答】解:M=(x﹣3)(x﹣7)=x2﹣10x+21,N=(x﹣2)(x﹣8)=x2﹣10x+16,M﹣N=(x2﹣10x+21)﹣(x2﹣10x+16)=5,则M>N.故选:B.3.观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187…,解答下列问题:3+32+33+…+32015的末位数字是()A.1 B.3 C.7 D.9【考点】尾数特征.【分析】根据31=3,32=9,33=27,34=81,35=243,36=729,37=2187…得出3+32+33+34…+32015的末位数字相当于:3+7+9+1+…+3+7+9,进而得出末尾数字.【解答】解:∵31=3,32=9,33=27,34=81,35=243,36=729,37=2187…∴末尾数,每4个一循环,∵2015÷4=503…3,∴3+32+33+34…+32015的末位数字相当于:3+7+9+1+…+3+7+9=(3+9+7+1)×503+19=10079的末尾数为9.故选:D.4.若实数x、y、z满足(x﹣z)2﹣4(x﹣y)(y﹣z)=0,则下列式子一定成立的是()A.x+y+z=0 B.x+y﹣2z=0 C.y+z﹣2x=0 D.z+x﹣2y=0【考点】完全平方公式.【分析】首先将原式变形,可得x2+z2+2xz﹣4xy+4xz+4y2﹣4yz=0,则可得(x+z﹣2y)2=0,则问题得解.【解答】解:∵(x﹣z)2﹣4(x﹣y)(y﹣z)=0,∴x2+z2﹣2xz﹣4xy+4xz+4y2﹣4yz=0,∴x2+z2+2xz﹣4xy+4y2﹣4yz=0,∴(x+z)2﹣4y(x+z)+4y2=0,∴(x+z﹣2y)2=0,∴z+x﹣2y=0.故选:D.5.已知△ABC中,AB=AC,高BD、CE交于点O,连接AO,则图中全等三角形的对数为()A.3 B.4 C.5 D.6【考点】等腰三角形的性质;全等三角形的判定.【分析】根据等腰三角形的性质以及全等三角形的判定和性质定理解答.【解答】解:∵高BD、CE交于点O,∴∠AEO=∠ADO=90°,图中的全等三角形有:①在△AEC与Rt△ADB中,,∴△AEC≌△ADB(AAS),∴∠ABO=∠ACO,∵AB=AC,∴∠ABC=∠ACB,∴∠CBO=∠BCO,∴OB=OC;②在△ABO与Rt△ACO中,,∴△ABO≌△ACO(SSS),∴∠BAO=∠CAO,③在△AEO与Rt△ADO中,,∴△AEO≌△ADO(AAS),④在△BOE与△COD中,,∴△BOE≌△COD(AAS);⑤在△BCE与△CBD中,∴△BCE≌△CBD(AAS).共有5对.故选C.6.如图,在△ABC中,∠C=90°,∠BAC=30°,AB=8,AD平分∠BAC,点PQ分别是AB、AD边上的动点,则PQ+BQ的最小值是()A.4 B.5 C.6 D.7【考点】轴对称﹣最短路线问题;含30度角的直角三角形.【分析】如图,作点P关于直线AD的对称点P′,连接QP′,由△AQP≌△AQP′,得PQ=QP′,欲求PQ+BQ的最小值,只要求出BQ+QP′的最小值,即当BP′⊥AC 时,BQ+QP′的值最小,此时Q与D重合,P′与C重合,最小值为BC的长.【解答】解:如图,作点P关于直线AD的对称点P′,连接QP′,在△AQP和△AQP′中,,∴△AQP≌△AQP′,∴PQ=QP′∴欲求PQ+BQ的最小值,只要求出BQ+QP′的最小值,∴当BP′⊥AC时,BQ+QP′的值最小,此时Q与D重合,P′与C重合,最小值为BC的长.在Rt△ABC中,∵∠C=90°,AB=8,∠BAC=30°,∴BC=AB=4,∴PQ+BQ的最小值是4,故选A.7.点P(3,﹣5)关于y轴对称的点的坐标为()A.(﹣3,﹣5)B.(5,3) C.(﹣3,5)D.(3,5)【考点】关于x轴、y轴对称的点的坐标.【分析】根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变可直接得到答案.【解答】解:点P(3,﹣5)关于y轴对称的点的坐标为(﹣3,﹣5),故选:A.8.下列四个命题中,真命题有()①两条直线被第三条直线所截,内错角相等.②如果∠1和∠2是对顶角,那么∠1=∠2.③三角形的一个外角大于任何一个内角.④如果x2>0,那么x>0.A.1个 B.2个 C.3个 D.4个【考点】命题与定理.【分析】根据平行线的性质对①进行判断;根据对顶角的性质对②进行判断;根据三角形外角性质对③进行判断;根据非负数的性质对④进行判断.【解答】解:两条平行直线被第三条直线所截,内错角相等,所以①错误;如果∠1和∠2是对顶角,那么∠1=∠2,所以②正确;三角形的一个外角大于任何一个不相邻的内角,所以③错误;如果x2>0,那么x≠0,所以④错误.故选A.二、填空题(每小题5分,共40分)9.若2a3x b y+5与5a2﹣4y b2x是同类项,则xy=﹣2.【考点】同类项.【分析】根据同类项的定义,含有相同的字母,相同字母的指数相同,即可列出关于x和y的方程组,求得x和y的值,进而求得代数式的值.【解答】解:根据题意得:,解得:,则xy=2×(﹣1)=﹣2.故答案为﹣2.10.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的度数为45°.【考点】平行线的性质.【分析】首先过点B作BD∥l,由直线l∥m,可得BD∥l∥m,由两直线平行,内错角相等,可得出∠2=∠3,∠1=∠4,故∠1+∠2=∠3+∠4,由此即可得出结论.【解答】解:过点B作BD∥l,∵直线l∥m,∴BD∥l∥m,∴∠4=∠1,∠2=∠3,∴∠1+∠2=∠3+∠4=∠ABC,∵∠ABC=45°,∴∠1+∠2=45°.故答案为:45°.11.如果(a2+b2+2)(a2+b2﹣2)=45,则a2+b2的值为7.【考点】换元法解一元二次方程.【分析】根据题意,可以设a2+b2=m,从而可以求得m的值,进而求得a2+b2的值,注意a2+b2的值不小于0.【解答】解:设a2+b2=m,则(m+2)(m﹣2)=45,∴m2﹣4=45,解得,m=7或m=﹣7,∴a2+b2=7或a2+b2=﹣7(舍去),故答案为:712.已知(a+25)2=1000,则(a+15)(a+35)的值为900.【考点】平方差公式.【分析】将(a+15)(a+35)变形为(a+25﹣10)(a+25+10),根据平方差公式得到原式=(a+25)2﹣100,再将(a+25)2=1000整体代入即可求解.【解答】解:(a+15)(a+35)=(a+25﹣10)(a+25+10)=(a+25)2﹣100,∵(a+25)2=1000,∴原式=1000﹣100=900.故答案为:900.13.计算(1﹣)()﹣(1﹣﹣)()的结果是.【考点】整式的混合运算.【分析】设a=1﹣﹣﹣﹣,b=+++,然后根据整式的乘法与加减混合运算进行计算即可得解.【解答】解:设a=1﹣﹣﹣﹣,b=+++,则原式=a(b+)﹣(a﹣)•b=ab+a﹣ab+b=(a+b),∵a+b=1﹣﹣﹣﹣++++=1,∴原式=.故答案为:.14.如图,在△ABC中,I是三内角平分线的交点,∠BIC=130°,则∠A=80°.【考点】三角形内角和定理.【分析】先根据角平分线的定义得到∠IBC=∠ABC,∠ICB=∠ACB,再根据三角形内角和定理得∠BIC+∠IBC+∠ICB=180°,则∠BIC=180°﹣(∠ABC+∠ACB),由于∠ABC+∠ACB=180°﹣∠A,所以∠BIC=90°+∠A,然后把∠BIC=130°代入计算可得到∠A的度数.【解答】解:∵BI、CI分别平分∠ABC、∠ACB,∴∠IBC=∠ABC,∠ICB=∠ACB,∵∠BIC+∠IBC+∠ICB=180°,∴∠BIC=180°﹣(∠IBC+∠ICB)=180°﹣(∠ABC+∠ACB),∵∠A+∠ABC+∠ACB=180°,∴∠ABC+∠ACB=180°﹣∠A,∴∠BIC=180°﹣=90°+∠A,∵∠BIC=130°,∴90°+∠A=130°∴∠A=80°.故答案为:80°.15.如图钢架中,焊上等长的13根钢条来加固钢架,若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是12°.【考点】等腰三角形的性质.【分析】设∠A=x,根据等边对等角的性质以及三角形的一个外角等于与它不相邻的两个内角的和求出∠AP7P8,∠AP8P7,再根据三角形的内角和定理列式进行计算即可得解.【解答】解:设∠A=x,∵AP1=P1P2=P2P3=…=P13P14=P14A,∴∠A=∠AP2P1=∠AP13P14=x,∴∠P2P1P3=∠P13P14P12=2x,∴∠P3P2P4=∠P12P13P11=3x,…,∠P7P6P8=∠P8P9P7=7x,∴∠AP7P8=7x,∠AP8P7=7x,在△AP7P8中,∠A+∠AP7P8+∠AP8P7=180°,即x+7x+7x=180°,解得x=12°,即∠A=12°.故答案为:12°.16.如图,AB=AC,则数轴上点C所表示的数为﹣1.【考点】勾股定理;实数与数轴.【分析】根据勾股定理列式求出AB的长,即为AC的长,再根据数轴上的点的表示解答.【解答】解:由勾股定理得,AB==,∴AC=,∵点A表示的数是﹣1,∴点C表示的数是﹣1.故答案为:﹣1.三、解答题(每小题10分,共40分)17.已知:3a=2,3b=6,3c=18,试确定a、b、c之间的数量关系.【考点】幂的乘方与积的乘方.【分析】根据同底数幂的乘法以及幂的乘方即可列出等式求出a、b、c之间的数量关系.【解答】解:∵2×18=62,∴3a×3c=(3b)2,∴3a+c=32b,∴a+c=2b18.已知a=2015x+2014,b=2015x+2015,c=2015x+2016.求a2+b2+c2﹣ab﹣bc﹣ca的值.【考点】因式分解的应用.【分析】原式变形后,利用完全平方公式配方后,将已知等式代入计算即可求出值.【解答】解:∵a=2015x+2014,b=2015x+2015,c=2015x+2016,∴a﹣b=﹣1,b﹣c=﹣1,a﹣c=﹣2,则原式=(2a2+2b2+2c2﹣2ab﹣2bc﹣2ac)= [(a﹣b)2+(b﹣c)2+(a﹣c)2]=×(1+1+4)=3.19.如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.(1)当∠BQD=30°时,求AP的长;(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.【考点】等边三角形的性质;全等三角形的判定与性质;含30度角的直角三角形.【分析】(1)由△ABC是边长为6的等边三角形,可知∠ACB=60°,再由∠BQD=30°可知∠QPC=90°,设AP=x,则PC=6﹣x,QB=x,在Rt△QCP中,∠BQD=30°,PC=QC,即6﹣x=(6+x),求出x的值即可;(2)作QF⊥AB,交直线AB于点F,连接QE,PF,由点P、Q做匀速运动且速度相同,可知AP=BQ,再根据全等三角形的判定定理得出△APE≌△BQF,再由AE=BF,PE=QF且PE∥QF,可知四边形PEQF是平行四边形,进而可得出EB+AE=BE+BF=AB,DE=AB,由等边△ABC的边长为6可得出DE=3,故当点P、Q运动时,线段DE的长度不会改变.【解答】解:(1)∵△ABC是边长为6的等边三角形,∴∠ACB=60°,∵∠BQD=30°,∴∠QPC=90°,设AP=x,则PC=6﹣x,QB=x,∴QC=QB+BC=6+x,∵在Rt△QCP中,∠BQD=30°,∴PC=QC,即6﹣x=(6+x),解得x=2,∴AP=2;(2)当点P、Q同时运动且速度相同时,线段DE的长度不会改变.理由如下:作QF⊥AB,交直线AB于点F,连接QE,PF,又∵PE⊥AB于E,∴∠DFQ=∠AEP=90°,∵点P、Q速度相同,∴AP=BQ,∵△ABC是等边三角形,∴∠A=∠ABC=∠FBQ=60°,在△APE和△BQF中,∵∠AEP=∠BFQ=90°,∴∠APE=∠BQF,,∴△APE≌△BQF(AAS),∴AE=BF,PE=QF且PE∥QF,∴四边形PEQF是平行四边形,∴DE=EF,∵EB+AE=BE+BF=AB,∴DE=AB,又∵等边△ABC的边长为6,∴DE=3,∴点P、Q同时运动且速度相同时,线段DE的长度不会改变.20.已知△ABC中,∠A:∠B:∠C=3:4:2,AD、BE是角平分线.求证:AB+BD=AE+BE.【考点】全等三角形的判定与性质.【分析】延长AB到F,使BF=BD,连DF,首先证明△ADF≌△ADC,推出AF=AC,由BE是角平分线,推出∠CBE=∠ABC=40°推出∠EBD=∠C,推出BE=EC,推出BE+AE=EC+AE=AC=AF=AB+BF=AB+BD.【解答】证明:延长AB到F,使BF=BD,连DF,∴∠F=∠BDF,∵∠A:∠B:∠C=3:4:2,∴∠ABC=80°,∠ACB=40°,∴∠F=40°,∠F=∠ACB,∵AD是平分线,∴∠BAD=∠CAD,在△ADF和△ADC中,,∴△ADF≌△ADC,∴AF=AC,∵BE是角平分线,∴∠CBE=∠ABC=40°∴∠EBD=∠C,∴BE=EC,∴BE+AE=EC+AE=AC=AF=AB+BF=AB+BD.∴AB+BD=AE+BE.2017年3月1日。
2019年“大梦杯”福建省初中数学竞赛试题参考答案(3)
被 9 除的余数只有 0 ,1, 2 , 7 , 8 这 5 种情形。 而 2019 3 ( mod 9 ) ,即 2019 被 9 除的余数为 3。
AC x ,则 AB x 6 。
∵ BC 10 , △ABC 的面积为 20 3 ,
∴ 1 BC AH 1 10 AH 20 3 , AH 4 3 。
2
2
∵ BH CH 10 ,
∴ (x 6)2 (4 3)2 x2 (4 3)2 10 。
又 x y z xyz ,
所以, z
xy xy 1
x x
x
x x
1 1
x 1
x
2
x
2
x
1
1
1 1 x
1 x22
3 4
。
由 x 1 ,知 0 1 1 x
所以, 1 1 ,即 x 2 时, z 取最大值 4 。(此时 y 2 )
2
这一结果为“陈氏定理”。陈景润勇攀科学高峰的精神和对“哥德巴赫猜想”研究的贡献,
激励了无数青年学子。
请你完成下列问题:
将 2019 分解为两个正立方数的和的分解方式有( )(即方程 2019 x3 y3 的正整数
解的组数)
A. 0 种
B.1种
C. 2 种 D. 3 种
【答案】 A
【解答】对任意正整数 m ,考察 m3 关于模 9 的余数。 由于对任意正整数 m , m 0 ,1,2 ,3 ,4 ,5 ,6 ,7 ,8 ( mod 9 ) 。
2018年“大梦杯”福建省初中数学竞赛试题参考答案及评分标准 (4)
2018年“大梦杯”福建省初中数学竞赛试题参考答案及评分标准考试时间 2018年3月18日 9∶00-11∶00 满分150分一、选择题(共5小题,每小题7分,共35分)。
每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。
请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.若关于x 的方程244310x mx m +--=有两个相等的实数根,则32442m m m ++-的值为( )A .3-B .2-C .1-D .1 【答案】 A【解答】依题意,21616(31)0m m =++=△。
因此,2310m m ++=。
∴ 231m m =--,231m m +=-。
∴ 3222442(31)44232123m m m m m m m m m ++-=--++-=+-=--=-。
2.如图,ABCD 、DEFG 都是正方形,边长分别为m 、n (m n <)。
坐标原点O 为AD 的中点,A 、D 、E 在y 轴上。
若二次函数2y ax =的图像过C 、F 两点,则nm=( ) A.1 B1 C.1 D.1 【答案】 B【解答】依题意,点C 坐标为()2mm ,,点F 的坐标为()2mn n -+,。
由二次函数2y ax =的图像过C 、F 两点,得222()2m am m n a n ⎧=⎪⎪⎨⎪+=-⎪⎩,消去a ,得2220n mn m --=。
∴ 2()210n n m m -⨯-=,解得1nm=(舍负根)。
∴1nm=。
(第2题图)3.如图,G 为ABC △的重心,点D 在CB 延长线上,且12BD BC =,过D 、G 的直线交AC 于点E ,则AEAC=( )A .25B .35C .37D .47【答案】 D【解答】如图,连AG ,并延长交BC 于点F 。
∵ G 为ABC △的重心,且12BD BC =, ∴ F 为BC 中点,且21AG GF =,DB BF FC ==。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年“大梦杯”福建省初中数学竞赛试题参考答案 考试时间 2017年3月19日 9∶00-11∶00 满分150分一、选择题(共5小题,每小题7分,共35分)。
每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。
请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.设2323a =++-,则1a a+的整数部分为( ) A .1 B .2 C .3 D .4 【答案】 B【解答】由22322323236a =+++⋅-+-=,知6a =。
于是1166a a +=+,2111()62866a a +=++=+,214()9a a <+<。
因此,1a a+的整数部分为2。
(注:4234233131232362222a +-+-=++-=+=+=) 2.方程22()32x x x +=-的所有实数根之和为( ) A .1 B .3 C .5 D .7 【答案】 A 【解答】方程22()32x x x +=-化为2222(2)3(2)x x x x -+=-。
即3251060x x x -+-=,2(1)(46)0x x x --+=。
解得1x =。
经检验1x =是原方程的根。
∴ 原方程所有实数根之和为1。
3.如图,A 、B 、C 三点均在二次函数2y x =的图像上,M 为线段AC 的中点,BM y ∥轴,且2MB =。
设A 、C 两点的横坐标分别为1t 、2t (21t t >),则21t t -的值为( )A .3B .23C .22±D .22 【答案】 D【解答】依题意线段AC 的中点M 的坐标为221212()22t t t t ++,。
(第3题)由BM y ∥轴,且2BM =,知B 点坐标为221212(2)22t t t t ++-,。
由点B 在抛物线2y x =上,知22212122()22t t t t++-=。
整理,得22221211222282t t t t t t +-=++,即221()8t t -=。
结合21t t >,得21t t -=4.如图,在Rt ABC △中,90ABC ∠=︒,D 为线段BC 的中点,E 在线段AB 内,CE 与AD 交于点F 。
若AE EF =,且7AC =,3FC =,则cos ACB ∠的值为( )A .37 B.7 C .314D.7【答案】 B【解答】如图,过B 作BK AD ∥与CE 的延长线交于点K 。
则由AE EF =可得,EBK EAF AFE BKE ∠=∠=∠=∠。
∴ EK EB =。
又由D 为BC 中点,得F 为KC 中点。
∴ 3AB AE EB FE EK KF FC =+=+===。
∴BC === ∴cos BC ACB AC ∠==。
或解:对直线AFD 及BCE △应用梅涅劳斯定理得,1BD CF EADC FE AB⋅⋅=。
由D 为线段BC 的中点,知BD DC =。
又AE EF =,因此,3AB CF ==。
结合7AC =,90ABC ∠=︒,利用勾股定理得,BC =所以,cos BC ACB AC ∠==。
DBA E(第4题)K5.如图,O 为ABC △的外接圆的圆心,R 为外接圆半径,且4R =。
直线AO 、BO 、CO 分别交ABC △的边于D 、E 、F ,则111AD BE CF++的值为( ) A .14 B .13 C .12 D .23【答案】 C【解答】由条件及等比定理,得OAB OAC OAB OAC OAB OAC ABD ACD ABD ACD ABCS S S S S S OA AD S S S S S ++====+△△△△△△△△△△△, 同理,OAB OBC ABCS S OB BE S +=△△△,OBC OACABC S S OC CF S +=△△△。
∴()()()2OAB OAC OAB OBC OBC OAC ABCS S S S S S OA OB OC AD BE CF S +++++++==△△△△△△△。
又4OA OB OC R ====, ∴ 111212AD BE CF R ++==。
二、填空题(共5小题,每小题7分,共35分)6.记函数223y x x =-+(12x -≤≤)的最大值为M ,最小值为m ,则M m +的值为 。
【答案】 8【解答】∵ 2223(1)2y x x x =-+=-+,12x -≤≤,∴ 1x =时,y 取最小值,即2m =;1x =-时,y 取最大值,即6M =。
∴ 8M m +=。
7.已知二次函数2y ax bx c =++(0a >)的图像与x 轴交于不同的两点A 、B , C 为二次函数图像的顶点,2AB =。
若ABC △是边长为2的等边三角形,则a = 。
【答案】【解答】依题意20ax bx c ++=有两个不同的实根,设为1x ,2x ,则122AB x x =-=。
∵ 12b x x a +=-,12cx x a=,∴ 222212121224()()4()44b c b ac x x x x x x a a a--=+-=--⨯==,即2244b ac a -=。
(第5题)又由222()24b b y ax bx c a x c a a =++=+-+,及0a >,知24b c a-+=即24b ac -=。
∴24a =,a =8.如图,在ABC △中,AD 为BC 边上的高,M 为线段BC 的中点,且BAD DAM MAC ∠=∠=∠。
若2AB =,则ABC △内切圆的半径为 。
【答案】1【解答】依题意,易知D 为BM 中点,12DM MC =。
又AM 平分DAC ∠, ∴12AD MD AC MC ==。
结合AD DC ⊥,得30ACD ∠=︒。
∴ 60DAC ∠=︒,90BAC ∠=︒。
∴AC =4BC =。
∴ ABC △内切圆半径为2412+=。
9.若二次函数2(43)3y x a x a =+-+(23a ≥)的图像与直线2y x =-在y 轴左侧恰有1个交点,则符合条件的所有a 的值的和为 。
【答案】2912【解答】依题意,关于x 的方程2(43)32x a x a x +-+=-,即2(42)320x a x a +-+-=恰有1个负根或者两个相等的负根。
有下列三种情形:(1)方程有两个相等的负根。
则212(42)4(32)0(42)0a a x x a ⎧=---=⎨+=--<⎩△,解得1a =或34a =。
均满足23a ≥。
因此,1a =,34a =符合要求。
(2)方程两根中一根为零,另一根为负数。
则1212320(42)0x x a x x a =-=⎧⎨+=--<⎩,解得23a =。
满足23a ≥。
B(第8题)因此,23a =符合要求。
(3)方程两根中一根为正数,另一根为负数。
则12320x x a =-<,解得23a <。
不满足23a ≥。
综合(1)、(2)、(3),得符合条件的a 的值为1,34,23。
因此,符合条件的所有a 的值的和为322914312++=。
10.若正整数n 恰有90个不同的正因数(含1和本身),且在n 的正因数中有7个连续整数,则正整数n 的最小值为 。
【答案】 25200【解答】∵ 任意连续7个正整数的乘积能被1234567⨯⨯⨯⨯⨯⨯整除, ∴ n 的正因数中必定有22,3,5,7这四个数。
∴ 正整数n 具有形式:12342357n αααα=⨯⨯⨯⨯(1α,2α,3α,4α为正整数,12α≥)。
由正整数n 恰有90个正因数,知1234(1)(1)(1)(1)90k αααα++++⨯=,其中k 为正整数。
而90分解为4个大于1的正整数的乘积的分解式只有一种:902335=⨯⨯⨯。
∴ 1k =,1234(1)(1)(1)(1)902335αααα++++==⨯⨯⨯。
∴ n 的最小值为422235725200⨯⨯⨯=,此时n 有连续正因数1,2,3,4,5,6,7。
三、解答题(共4题,每小题20分,共80分) 11.求方程2220172018x y x +=的正整数解。
【解答】方程化为22201820170x x y -+=。
将方程视为x 的方程,得22222018420174(10092017)y y =-⨯=-△为完全平方数。
…………………… 5分∴ 2210092017y -为完全平方数。
设22210092017y t -=(t 为非负整数),则22210092017t y -=。
∴ 2(1009)(1009)2017t t y -+=。
∵ 2017为质数,∴ 2017(1009)t -,或2017(1009)t +。
…………………… 10分 又t 为非负整数,且1009t ≤。
∴ 1009t =,或1008t =。
…………………… 15分 ∴ 0y =(舍去),或1y =。
将1y =代入方程,得2201820170x x -+=,解得1x =,或1017x =。
∴ 原方程的正整数解为11x y =⎧⎨=⎩,或20171x y =⎧⎨=⎩。
…………………… 20分12.如图,在等腰三角形ABC中,90ACB∠=︒,M是边AC的中点,D是边BC上一点,直线AD、BM交于点E,且ME MA=。
求证:(1)BE CD=;(2)AC DE AD DB=。
【解答】(1)如图,连结CE。
由条件知,ME MA MC==。
∴CE AE⊥。
…………… 5分∵90ACB∠=︒,∴MAE DCE∠=∠。
∴BED AEM MAE DCE ∠=∠=∠=∠。
又EBD CBE∠=∠,∴BDE BEC△∽△。
∴BE DEBC EC=。
…………… 10分又由CE AD⊥,AC CD⊥,知CDE ACE△∽△。
∴CD DE AC CE=。
由此可得,BE DE CDBC EC AC==,即BE CDBC AC=。
∵BC AC=,∴BE CD=。
…………… 15分(2)由(1)CE AD⊥,AC CD⊥,知CDE ADC△∽△,∴CE AC CD AD=。
又由(1)BDE BEC△∽△,知DE EC DB EB=。
结合(1)中BE CD=,可得AC CE EC DE AD CD EB DB===。
∴AC DEAD DB=。
…………… 20分(第12题)13.若存在正整数n ,p (6p >)使得3246n n n n p ⎧⎫⎧⎫⎧⎫⎧⎫+++=⎨⎬⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭⎩⎭成立,其中{}[]x x x =-,[]x 为不超过x 的最大整数。
(1)求p 的最小值;(2)当p 取最小值时,求使3246n n n n p ⎧⎫⎧⎫⎧⎫⎧⎫+++=⎨⎬⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭⎩⎭成立,且2017n ≤的正整数n的个数。
