第二章 液体界面性质(1)
合集下载
第二章 液体界面性质(2)
（1-72） 72）
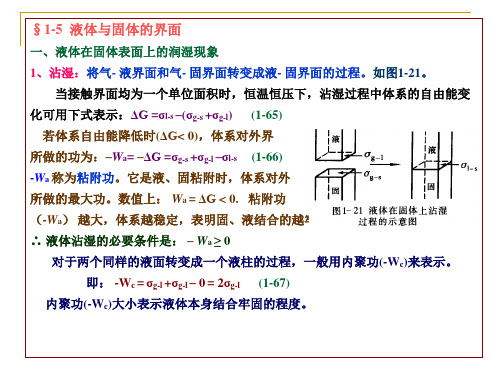
液体可在固体表面上自动铺展。 当S≥0，即A ≥σl-g 时，体可在固体表面上自动铺展。 ， σ 应用上述公式计算时，需要三种界面张力常数，而实际上只有σ 应用上述公式计算时，需要三种界面张力常数，而实际上只有σl-g 可通过实验测得，故不可能作为实际工作中的判别依据. 可通过实验测得，故不可能作为实际工作中的判别依据.
四、影响接触角测定的因素
1、接触角滞后 、 图1-32 θA –增加表面时测得的接触角，称为前进角。 增加表面时测得的接触角，称为前进角 前进角。 θR—减少表面时测得的接触角，称为后退角。 减少表面时测得的接触角，称为后退角 后退角。 θA –θR值称为接触角滞后。 值称为接触角滞后。 接触角滞后 原因：表面不洁；表面粗糙；润湿不够。 原因：表面不洁；表面粗糙；润湿不够。 因为实验中很难避免空气中的气体被吸附。 因为实验中很难避免空气中的气体被吸附。 例如：在各种气体中， 例如：在各种气体中，水在金表面上的前进角和 后退角测定值既有较大区别。 后退角测定值既有较大区别。
3、铺展： 、铺展： 3、指液固 界面取代气 固界面的同时，气-液界面也扩大同样面积的过 、指液固-界面取代气 固界面的同时， 液界面也扩大同样面积的过 铺展 界面取代气-固界面的同时 程。图1-23。 。 在恒温恒压下，设铺展面积为一个单位面积，铺展过程中体系的自 恒温恒压下，设铺展面积为一个单位面积， 由能的降低可用下式表示： 由能的降低可用下式表示： (1ΔG =（σl-s+σl-g）–σg-s (1-71a) 或体系对外所做的功可用 表示 或体系对外所做的功可用S表示： 对外所做的功可用 表示： S = σg-s–(σl-s+σl-g） (1-71) (1式中： 铺展系数。 式中：S- 铺展系数。 液体可在固体表面上自动铺展。 当S≥0（ ΔG≤0）时，液体可在固体表面上自动铺展。 （ ） 式代入到1-71式中，可得到粘附力与铺展系数之间的关系： 式中， 将1-70式代入到 式代入到 式中 可得到粘附力与铺展系数之间的关系： S = A-σlg
第二章液体表面
在特定条件下，
γ＝( ∂G ∂A
)T .P
=
( ∂F ∂A
) T.V
=
(
∂H ∂A
) S.P
=
(
∂U ∂A
) S.V
γ的意义： 在各种特定条件下，可逆地改变单位面积时所引起体系自由
能、功函、热焓和内能的改变（增量）。
2008年11月17日
第二章 液体表面
3
Monday
第二章 液体表面
γ＝
(
∂G ∂A
解：根据表面能的概念
( ∂U ∂A
) T .P
=
γ
− T ( ∂γ ∂T
) A.P
T = 273 + 1535 = 1808 K
γ =1 8 8 0 m N / m, ， ( ∂ γ ) = －0.43 m N / m k
∂T
则
∂U ( ∂A )T .P
=γ
−
T
∂γ
( ∂T
) A.P
= 1880
− 1808
γ
γ
γ
γ
UP
UP
γ
γ
平面：表面张力 相互抵消，液面 内外压力相等。
凸面：由于γ不 能相互抵消，产 生ΔP，方向向内。
凹面：由于γ不能 相互抵消，产生 ΔP，方向向外。
2008年11月17日
第二章 液体表面
18
Monday
第二章 液体表面
ΔP：附加压力，对于非平面液体，由于表面张力的作用，都要产生附 加压力ΔP。 液滴，凸液面：ΔP指向液滴内部， P凸﹦p0＋ ΔP。
例外: Cu, Zn, Fe, Cd 及其合金，硅酸盐类物质，T↑, γ↑
4）压力的影响 压力对γ的影响数据减少，问题也复杂得 多。 一般说来，压力增加，表面张力下降。
液体界面性质
2 r f or 2 r f
f为校正因子，r为毛细管外口半径。
滴体积法的装置
液滴滴落时的快速照相图
⑸ 挂片法。 至少有一种 会用
W W总 W环 2l
W 2l
挂片法示意图
1.4
表面热力学
1.4.1 Gibbs表面热力学 两种完全不互溶的液体，在平衡时，两相间存在界面层。 这个界面是无厚度的几何分界面，即SS’.
i i i
dF dF dF dF S dT pdV i dni S dT pdV i dni
i i
S dT dA i dni
i
dG dG dG dG S dT V dp i dni S dT V dp i dni
i i
S dT dA i dni
i
dU TdS dA i dni Nhomakorabeai
平衡时：
dH TdS dA i dni dF S dT dA i dni
i i
dG S dT dA i dni
表面能 1J / m2 1107 erg /104 cm 2 1103 erg / cm 2
G
U
H
F
表面张力 1N / m 1 105 dyn /102 cm 1103 dyn / cm 常用单位 1mN / m 1dyn / cm
1.1.3 影响表面张力的因素
SA可以改变液体对固体的润湿性，如下图示：
能使固体表面产生润湿转化的活性剂，称为润湿剂。 渗透：是液体进入多孔性固体介质中的过程。 当θ>90°时，难以渗透。加入润湿剂使表面发生润湿转化，使θ<90° ，这就可以进行渗透。这种润湿剂也称为渗透剂。
第1章液体界面 第2章固体界面性质
由于恒温恒压下环境对系统做的可逆非体积功等于系统 的吉布斯函数改变，即 也是恒温恒压下系统增加单位面积时 所增加的吉布斯函数，称为表面吉布斯 自由能，单位为 J m2 。
Wr ' dGT , p dAs
G A s T , p
.热力学公式 多组分多相系统，再将各相界面面积 As 作为变量， 若只考虑一个相界面，并且两相温度、压力相同，相应 的热力学基本公式为
表面张力 就是垂直作用于单位长度的边界上的引起液体表面
1 收缩的力。 N m 单位是
表面张力的方向 是和液面相切，并和两部分的分界线垂直。 如果液面是平面，表面张力就在平面上，见图。 如果液面是曲面，表面张力则在这个曲面的切面上，见图。
表面张力的定量描述实验
2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l 2 l
B
B
B
B
G U H A A A A As T ,V ,nB ( ) s T , p ,nB ( ) s S ,V ,nB ( ) s S , p ,nB ( )
4. 表面张力的影响因素 （1）表面张力与物质本性的关系
不同物质分子间作用力不同，对表面分子的影响也不同。 不同液体表面张力的差异主要是不同液体分子间作用力不同。
一般情况下，非极性液体较小，极性液体表面张力较大， 熔融盐和熔融金 属（离子键、金属键）表面张力很高。 20℃ 水 72.75 乙醇 22.3 乙醚 17.0 汞 25℃ 485.48 氯化钠 803℃ 113.8 氧化亚铁 1427℃ 582 氧化铝 2080℃ 700 银 1100℃ 878.5 铜 1084.6℃ 1300 ／mN.m-1
材料表界面第二章液体表面
• 由热力学第二定律，dQR=Tdห้องสมุดไป่ตู้，得：
dU TdS PdV σdA (2 6)
2.2 表面张力的热力学定义
• 根据焓：H=U+pV, 自由能：F=U-TS 自由焓：G≡H-TS 微分得： dH=dU+PdV+VdP dF=dU-TdS-SdT dG＝dH-TdS-SdT
导出表界面张力的热力学方程：
W
4
r12
(
r1 r2
1)
4.85101 Jm2 4 3.1416 (103 m)2 (105 1)
6.09101 J
2.2 表面张力的热力学定义
• 热力学第一定律告诉我们可逆条件下生 成单位表面时内能的变化:
dU=dQR dWR (2 5)
• 系统功包括膨胀功和表面功:
dWR pdV σdA
2.1表面张力和表面自由能
表面张力示意：
如果在金属线框中间系一线圈，一 (a)
起浸入肥皂液中，然后取出，上面形 成一液膜。
由于以线圈为边界的两边表面张
力大小相等方向相反，所以线圈成任
意形状可在液膜上移动，见(a)图。
•表面张力的作用
(b)
如果刺破线圈中央的液膜，线圈
内侧张力消失，外侧表面张力立即将 线圈绷成一个圆形，见(b)图，清楚的 显示出表面张力的存在。
理想表面
清洁表面
吸附表面
清洁表面:指不存在任何污染的化学纯表面，即不存 在吸附、催化反应或杂质扩散等物理化学效应的表 面。表面上会发生与体内结构和成分不同的变化。
结构变化
驰豫
指表面层之间以及表面和体 内原子层之间的垂直间距ds 和体内原子层间距d0相比有 所膨胀和压缩的现象。可能 涉及几个原子层。
dU TdS PdV σdA (2 6)
2.2 表面张力的热力学定义
• 根据焓：H=U+pV, 自由能：F=U-TS 自由焓：G≡H-TS 微分得： dH=dU+PdV+VdP dF=dU-TdS-SdT dG＝dH-TdS-SdT
导出表界面张力的热力学方程：
W
4
r12
(
r1 r2
1)
4.85101 Jm2 4 3.1416 (103 m)2 (105 1)
6.09101 J
2.2 表面张力的热力学定义
• 热力学第一定律告诉我们可逆条件下生 成单位表面时内能的变化:
dU=dQR dWR (2 5)
• 系统功包括膨胀功和表面功:
dWR pdV σdA
2.1表面张力和表面自由能
表面张力示意：
如果在金属线框中间系一线圈，一 (a)
起浸入肥皂液中，然后取出，上面形 成一液膜。
由于以线圈为边界的两边表面张
力大小相等方向相反，所以线圈成任
意形状可在液膜上移动，见(a)图。
•表面张力的作用
(b)
如果刺破线圈中央的液膜，线圈
内侧张力消失，外侧表面张力立即将 线圈绷成一个圆形，见(b)图，清楚的 显示出表面张力的存在。
理想表面
清洁表面
吸附表面
清洁表面:指不存在任何污染的化学纯表面，即不存 在吸附、催化反应或杂质扩散等物理化学效应的表 面。表面上会发生与体内结构和成分不同的变化。
结构变化
驰豫
指表面层之间以及表面和体 内原子层之间的垂直间距ds 和体内原子层间距d0相比有 所膨胀和压缩的现象。可能 涉及几个原子层。
《液体的界面》ppt课件
液体区别于气体的主要特征之一：是它 和空气接触处有一个自在外表，和固体、 器官组织接触处有一个附着层。
在液体内部由于分子的紊乱运动， 液体在各个方向的物理性质都是完全 一样的，即各向同性。
在液体的外表，无论是在液体与空 气之间的自在外表，或是在两种不能混 合的液体之间的界面，或是在液体与固 体之间的界面，各个方向的物理性质就 不一样，即各向异性。
肺泡上外表活性物质对外表张 力系数的调控作用，保证了呼吸过 程的正常进展。
实验阐明，正常呼气后，肺泡 通常稳定在它最大尺寸的1/4， 即肺内还有余气，这使接下来 的吸气变得容易一些。
在国际单位制中，α的单位是〔N·m-1〕。
外表张力系数α与液体的性质和温度有关， 液体的α值还与液体的纯真度有关。
液体外表张力产生的缘由，可以用液体分 子间相互作用的分子力来加以解释。不同的液 体，分子间的相互作用力不同。分子间相互作 用力愈大，相应的外表张力系数就愈大。
一切位于外表层内的液体分子，都要遭 到垂直液面并指向液体内部的分子引力的作 用。外表层内的分子比液体内部的分子具有 更多的势能。
由上式可知在数值上等于增加单位液面时外力所作的功从能量的角度看其大小等于增加单位液面时所增加的表面自由能
第七章 分子动实际
第五节 液体的外表景象
一、 液体的界面
液体与气体的差别——气体分子间的 间隔通常较大，而液体分子间的间隔 缩短了，分子力的作用显著添加，液 体分子由于相互吸引，表现出气体分 子所没有的内聚力和自在外表。
对于不润湿管壁的液体，在毛细管 内的液面是凸的，液面内的压强高于液 面外的压强，管内的液面将下降至管外 液面之下，其高度差也可用上式计算， 此时接触角θ>π/2，故所得h为负，表示 管中液面下降。
专题一液体界面性质
方法特点 本法相对简单, 但操作需相当熟练,且仅适用于药液颜色较浅的制剂。
8 光散射法 测定原理 光线通过表面活性剂溶液时,如果溶液中有胶束粒子存在, 则一部分光
线将被胶束粒子所散射, 因此, 测定散射光强度即浊度,可反映溶液中表面活性剂胶 束形成。以药液的浓度c为X轴,光散射强度I为Y轴, 做出I2c关系曲线。当表面活性 剂在溶液中达到或超过一定浓度时,会从单体(单个离子或分子)缔合成胶态聚集物, 即形成胶束, 其大小符合胶粒大小的范围,故有光的散射现象。随着表面活性剂浓 度的增大,缔和分子不断增多, 胶束聚集数不断增加, 则药液的光散射强度不断增强。 达CMC 时,光散射强度急剧增加, CMC即可由曲线的突变点求出。
方法特点 该方法简单、准确而有效, 可测定多种表面活性剂(特别是混合表面活
性剂体系)的CMC值。由于该方法受盐类等杂质影响较小,因此,可以用于纯度不高 的工业用混合表面活性剂CMC值的测定。
5 染料吸附法
由于某些染料被胶团增溶时,其吸收光谱与未增溶时发生明显改 变, 故其颜色有明显差别, 所以, 只要在大于CMC 的表面活性剂溶液中加入少量 染料, 然后定量加水稀释至颜色改变即可判定CMC 值。采用滴定终点观察法或 分光光度法均可完成测定。此法的关键是必须选择合适的染料:根据同性电荷相 斥,异性电荷相吸的原理, 选取与表面活性离子电荷相反的染料(一般为有机离 子) 。例如: 常用于阴离子(负离子)表面活性剂的染料有频那氰醇氯化物、碱性 蕊香红G等。具体方法:先在确定浓度( > CMC )的表面活性剂溶液中加入少量 G : ( ) 染料, 此时染料被溶液中的胶束吸附而使溶液呈现某种颜色。再用滴定法以水 冲稀此溶液, 直至溶液颜色发生显著变化。由被滴定溶液的总体积可方便求得 CMC。
液体界面的性质
液体界面的性质1、液体的铺展：某液体1是否能在另一互不相溶的液体2上铺展开来，取决于各液体本身的表面张力和(3为气相）以及两液体之间的界面张力的大小。
下图是液滴1在另一液体2上的情况。
图中3为气相。
设考虑三个相接界A点处的和的作用是力图维持液滴成球型(由于地心引力可能成透镜形状)，而的作用则是力图使液体铺展开来。
因此如果则液体1可以在液体2上铺展开来。
若液体2是水，则一般很大，在这种界面上，大多数有机液体1都可铺成薄膜。
2.表面张力与溶质的关系表面张力与溶质的关系：水的表面张力因加入溶质形成溶液而改变。
有些溶质加入水中后使溶液表面张力升高。
例如无机盐、不挥发性的酸碱(如H2SO4、NaOH)等，由于这些物质的离子，对于水分子的吸引而趋向于把水分子拖入溶液内部，此时在增加单位表面积所作的功中，还必须包括克服静电引力所消耗的功，因此溶液的表面张力升高。
这些物质被称为非表面活性剂。
有些溶质加入水中后使溶液表面张力下降，能使水的表面张力降低的溶质都是有机物。
我们习惯上把那些明显降低水的表面张力的具有两亲性质的有机化合物叫做表面活性剂。
3.两亲性质所谓两亲分子，以脂肪酸为例，亲水的-COOH基使脂肪酸分子有进入水中的趋势，而憎水的碳氢链则竭力阻止其在水中溶解。
这种分子就有很大的趋势存在于两相界面上，不同基团各选择所亲的相而定向，因此称为两亲分子。
进入或“逃出”水面趋势的大小，决定于分子中极性基与非极性基的强弱对比。
对于表面活性物质来说，非极性成分大，则表面活性也大。
由于憎水部分企图离开水而移向表面，所以增加单位表面所需的较之纯水当然要小些，因此溶液的表面张力明显降低。
4.特劳贝(Traube)规则特劳贝(Traube)规则：特劳贝在研究脂肪酸同系物的表面活性物质时发现：同一种溶质在底浓度时表面张力的降低效应和浓度成正比。
不同的酸在相同的浓度时，对于水的表面张力降低效应（表面活性）随碳氢链的增长而增加。
每增加一个-CH2-，其表面张力效应平均可降低约3.2倍。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
式中： 液体摩尔体积， 式中：Vm -液体摩尔体积， Vm = M/ρ
ρ-液体在t温度下的密度; M-摩尔质量； 液体在t温度下的密度; -摩尔质量；
k –温度系数 （非极性液体: 2.2 x10-7J/K) 非极性液体:
② 古根汉姆(Guggenheim)经验公式： 古根汉姆(Guggenheim)经验公式： (Guggenheim)经验公式 σ=σ[( tc- t )/tc ] n 热力学关系式： ③ 热力学关系式： 有机液体： 有机液体：n =11/9 ；金属液体：n = 1 金属液体： （dH/dA)T,P =γ -T(dγ/dT)A,P
式中： 式中：
ΔVa -表示有吸附引起的体积变化 由表面相及体相密度差引起的体积变化。 ΔVs - 由表面相及体相密度差引起的体积变化。
ห้องสมุดไป่ตู้
研究表明： 研究表明：当ΔVa为控制项时，则p↗; γ↙; Va为控制项时， 为控制项时 ↗; 当ΔVs 控制时 则p↗; γ↗。 ↗; 上式表明：在恒温恒表面积条件下，压力对表面张力的影响等于 上式表明：在恒温恒表面积条件下， 在恒温恒压下增加单位表面时， 在恒温恒压下增加单位表面时，相应数量的分子从体相中移到表面相 时体积的变化。 时体积的变化。
二、 表面张力 二、表面张力 所示， 将铂丝从液面上拉到高度h处 如图1- 2所示，如果用拉力 将铂丝从液面上拉到高度 处， 所示 如果用拉力F将铂丝从液面上拉到高度 在此过程中外力对体系所作的功 W=F•h 由于体系增加的表面积 = 2l • h ∴体系增加的自由能 G = 2 l • hσ， 在可逆条件下既有： 在可逆条件下既有： W = G 2 l • hσ =F • h ∴
第二章
§2-1 表面能与表面张力 一、表面能
液体界面性质
1、一种表面单组分体系
第二章
液体界面性质
纯液体体系中， 纯液体体系中，液体内部的分子和液体表面上的分子所受的作用力是不同的 (见图 见图1-1)， 内部分子受到的合力为零；而液体表面上的分子受到一个指向内部的 见图 ， 内部分子受到的合力为零； 拉力，所以液体表面有自动收缩的趋向，在没有外力情况下， 拉力，所以液体表面有自动收缩的趋向，在没有外力情况下，它的形状总是取球 形 最稳定。 最稳定。 纯液体在恒温、恒压的条件下， 纯液体在恒温、恒压的条件下，可逆的 增加体系的表面积, 增加体系的表面积 则环境对体系所作的功 δG(自由能 与表面积的增量δA 成正比： 自由能) 与表面积的增量δ 成正比： 自由能 = 则 σ=（δG /δA）T，P （1-1） δ 式中： 式中：σ-称为表面能 单位： 单位：mJ/m2 or mN/m or g/s2 液体表面能的定义：纯液体在恒温、恒压的条件下， 液体表面能的定义：纯液体在恒温、恒压的条件下，可逆的变化单位表面积 表面能的定义 所 引起的体系自由能变化量。 引起的体系自由能变化量。
五、化学组分影响
研究表明：恒温下非缔合液体气液平衡时， 研究表明：恒温下非缔合液体气液平衡时，表面张力γ 与气液两相密度之间 有如下关系： 有如下关系： 式中： 液体摩尔质量 液体摩尔质量； 等张比容。 式中： M-液体摩尔质量； [P] – 等张比容。 式中： 式中： M/ρ- 液体摩尔体积 (cm3/mol)。 。 从一级近似来说，有机物的 从一级近似来说，有机物的[P] 与其空间结构无关， 与其空间结构无关，而只取决于其 化学成分和结构单元。 化学成分和结构单元。有机物中原 子和结构单元的等张比容见表3-3。 子和结构单元的等张比容见表 。 某一有机物的[P] 可由下式计算： 可由下式计算： 某一有机物的 [P] =Σ[P]原子+Σ[P]结构单元 当温度远离临界温度时， 当温度远离临界温度时，ρ–ρ0 →ρ 上式可简化为： 上式可简化为：
五、化学组分影响
[P]的物理意义：在表面张力γ =1的温度下，液体摩尔体积即为等张比容。 的物理意义： 的温度下， 等张比容。 的物理意义 的温度下 液体摩尔体积即为等张比容
已知20℃ 戊烯的密度为0.640, 试求：1-戊烯的表面张力 。 试求： 戊烯的表面张力 戊烯的表面张力γ 例题 已知 ℃时1-戊烯的密度为 戊烯的密度为 例题 有机物等张比容计算 先求等张比容： 解： 先求等张比容： [P] =Σ[P] 原子+Σ[P]结构单元 = 5 [P] C+10 [P] H+ [P] = +10 [P]– =5x 9 +10x15. 5 +19 –10x 9. 5 =124 [实测值 123.8] 实测值
σ = F/ 2 • l
(1-9)
由上式可见，表面能又是作用在单位长度上液体表面的收缩力， 由上式可见，表面能又是作用在单位长度上液体表面的收缩力，这种力称 为表面张力（γ） 表面张力（ 物理学的定义：沿液体表面垂直作用于单位长度上的紧缩力。 γ物理学的定义：沿液体表面垂直作用于单位长度上的紧缩力。 表面张力的方向 和液体表面相切；和净吸力垂直。 和液体表面相切；和净吸力垂直。 20℃时常见液体表面张力（见表1.1） 20℃时常见液体表面张力（见表1.1） 1.1
分别为液体 液体a 液体b在相互饱和时的表面张力。 式中 γa ,γb --分别为液体a和液体b在相互饱和时的表面张力。 规则的验证： 作 Antonow 规则的验证：
二、相界面性质
其中: 苯 水 (实测值 实测值34.4) 其中: γ苯/水 = |γ水 - γ苯| = 63.2 - 28.8 = 34.4 (实测值34.4) 水 苯 由表中数据可见， 要小很多。 由表中数据可见，界面张力比表面张力γ要小很多。 戊醇/ 降到4. 其中最突出的是戊醇 水的界面张力降到 其中最突出的是戊醇/水的界面张力降到 8 mN/m.
§2-1 表面能与表面张力 一、表面能
2、一种表面两组分体系 、
一、表面能 两组分组成， 恒定时，体系的表面能的定义 若体系由 m和n两组分组成，当组分 n 恒定时，体系的表面能的定义 和 两组分组成
式：
σ=（δG /δA）T.P, n （1-5） （ ） ）
物理意义：在恒温、恒压和恒组分 的条件下 的条件下， 物理意义：在恒温、恒压和恒组分n的条件下，可逆的变化单位表面 积所引起的体系自由能变化量。 积所引起的体系自由能变化量。 由此可见，体系的表面能不但与温度压力有关， 由此可见，体系的表面能不但与温度压力有关，而且随体系中组分的 改变而改变。 改变而改变。
表1.1 一些纯液体的表面张力
从表中数据可见： 从表中数据可见： Hg的 最大485.5 水是次之。 485.5， ① 常见纯液体中 Hg的γ值最大485.5，水是次之。 ② 有机液体 表面张力在50～60mN/m， 且γ极性 >γ非极性 表面张力在 ～ ，
§2-2 影响表面张力的因素
一、物质本性（分子间吸引力） 物质本性影响表面张力的因素 液体分子间的吸引力↗， σ值↗ 液体分子间的吸引力↗ §2-2 （分子间吸引力） 液体名称： 液态Cu(1100 Cu(1100℃ 液体名称： 水 正己烷 Hg 液态Cu(1100℃) 一、物质本性 二、相界面性质 ： N/m） γ值（m N/m） 72.75 18.4 485 879 二、相界面性质 当两种液体接触时，其界面张力γa/ b 可用安东诺夫（Antonow）规 当两种液体接触时，其界面张力 可用安东诺夫（Antonow） 则计算： 则计算：
3、多种界面多组分体系 、
表面能的定义式： 表面能的定义式： σi =（δG /δA）T.P, ni, Aj≠i （1-6） （ ） ） 物理意义:在恒温、恒压和恒组分n的条件下，可逆的变化第i 种单位 物理意义 在恒温、恒压和恒组分 的条件下，可逆的变化第 在恒温 的条件下 界面所引起的体系自由能变化量。 界面所引起的体系自由能变化量。
Antonow 规则的验证
三、温度影响 体系的温度↗ 分子间引力↙ 体系的温度↗；分子间引力↙； γ↙（图1-3）。 当温度升高接近液体临界温度( 近似等于沸点) 当温度升高接近液体临界温度(tc 近似等于沸点) 时，液-气界面逐渐消失，此时γ→0。 气界面逐渐消失，
γ- t 的经验关系式： 的经验关系式：
三、温度影响 三、温度影响 三、温度影响 三、温度影响
约特弗斯(Eötvös)公式： (Eötvös)公式 ① 约特弗斯(Eötvös)公式： γVm2/3 =k (tc -t)
表1.2 温度对液体表面张力的影响
四、压力影响 通常， ↗; 影响不大； 通常，p↗; 对γ影响不大； 例如：20℃ 例如：20℃ 1atm σH2O = 72.75 ; σCCl4 = 26.8 四、压力影响 10atm σH2O = 71.75 ; σCCl4 = 25.8 在热力学上可以导出如下公式： 在热力学上可以导出如下公式：
∵
∴γ={ρ[P] /M }4 = { 124 x 0.64/70 }4 = 1. 65
§2-3 弯曲液面现象
§2-3 一、弯曲液面下附加压力(Δ弯曲液面现象 弯曲液面下附加压力( P)
1、凸液面 由于液体的表面张力总是力图收缩 液体的体积， 液体的体积，∴液体表面产生向着液体 内部的附加压力Δ 其数值为液面内、 内部的附加压力ΔP，其数值为液面内、 外压力之差， 外压力之差， 即：ΔP = P凸液 - P气, 且ΔP > 0 2、凹液面 如图1 4(b)所示 如图1-4(b)所示 ∴ P凹液 < P气 此时 ΔP< 0 凹液面内的附加压力与凸液面正好相反，附加压力Δ 凹液面内的附加压力与凸液面正好相反，附加压力ΔP = P凹液- P气 ，由于 液面内的压力有使凹面变成平面的趋势， 液面内的压力有使凹面变成平面的趋势， 结论: 结论: 附加压力Δ 的方向总是指向曲率中心； (1) 附加压力ΔP的方向总是指向曲率中心； 向着曲率中心一侧的压力总是比弯曲液面另一侧压力大。 (2) 向着曲率中心一侧的压力总是比弯曲液面另一侧压力大。 3、平液面 由于表面张力沿着平面作用，表面收缩力向四方展开并相互抵消， 由于表面张力沿着平面作用，表面收缩力向四方展开并相互抵消，∴ΔP = 0 如图1 4(a)所示 如图1-4(a)所示 一、弯曲液面下附加压力(ΔP) 弯曲液面下附加压力(
ρ-液体在t温度下的密度; M-摩尔质量； 液体在t温度下的密度; -摩尔质量；
k –温度系数 （非极性液体: 2.2 x10-7J/K) 非极性液体:
② 古根汉姆(Guggenheim)经验公式： 古根汉姆(Guggenheim)经验公式： (Guggenheim)经验公式 σ=σ[( tc- t )/tc ] n 热力学关系式： ③ 热力学关系式： 有机液体： 有机液体：n =11/9 ；金属液体：n = 1 金属液体： （dH/dA)T,P =γ -T(dγ/dT)A,P
式中： 式中：
ΔVa -表示有吸附引起的体积变化 由表面相及体相密度差引起的体积变化。 ΔVs - 由表面相及体相密度差引起的体积变化。
ห้องสมุดไป่ตู้
研究表明： 研究表明：当ΔVa为控制项时，则p↗; γ↙; Va为控制项时， 为控制项时 ↗; 当ΔVs 控制时 则p↗; γ↗。 ↗; 上式表明：在恒温恒表面积条件下，压力对表面张力的影响等于 上式表明：在恒温恒表面积条件下， 在恒温恒压下增加单位表面时， 在恒温恒压下增加单位表面时，相应数量的分子从体相中移到表面相 时体积的变化。 时体积的变化。
二、 表面张力 二、表面张力 所示， 将铂丝从液面上拉到高度h处 如图1- 2所示，如果用拉力 将铂丝从液面上拉到高度 处， 所示 如果用拉力F将铂丝从液面上拉到高度 在此过程中外力对体系所作的功 W=F•h 由于体系增加的表面积 = 2l • h ∴体系增加的自由能 G = 2 l • hσ， 在可逆条件下既有： 在可逆条件下既有： W = G 2 l • hσ =F • h ∴
第二章
§2-1 表面能与表面张力 一、表面能
液体界面性质
1、一种表面单组分体系
第二章
液体界面性质
纯液体体系中， 纯液体体系中，液体内部的分子和液体表面上的分子所受的作用力是不同的 (见图 见图1-1)， 内部分子受到的合力为零；而液体表面上的分子受到一个指向内部的 见图 ， 内部分子受到的合力为零； 拉力，所以液体表面有自动收缩的趋向，在没有外力情况下， 拉力，所以液体表面有自动收缩的趋向，在没有外力情况下，它的形状总是取球 形 最稳定。 最稳定。 纯液体在恒温、恒压的条件下， 纯液体在恒温、恒压的条件下，可逆的 增加体系的表面积, 增加体系的表面积 则环境对体系所作的功 δG(自由能 与表面积的增量δA 成正比： 自由能) 与表面积的增量δ 成正比： 自由能 = 则 σ=（δG /δA）T，P （1-1） δ 式中： 式中：σ-称为表面能 单位： 单位：mJ/m2 or mN/m or g/s2 液体表面能的定义：纯液体在恒温、恒压的条件下， 液体表面能的定义：纯液体在恒温、恒压的条件下，可逆的变化单位表面积 表面能的定义 所 引起的体系自由能变化量。 引起的体系自由能变化量。
五、化学组分影响
研究表明：恒温下非缔合液体气液平衡时， 研究表明：恒温下非缔合液体气液平衡时，表面张力γ 与气液两相密度之间 有如下关系： 有如下关系： 式中： 液体摩尔质量 液体摩尔质量； 等张比容。 式中： M-液体摩尔质量； [P] – 等张比容。 式中： 式中： M/ρ- 液体摩尔体积 (cm3/mol)。 。 从一级近似来说，有机物的 从一级近似来说，有机物的[P] 与其空间结构无关， 与其空间结构无关，而只取决于其 化学成分和结构单元。 化学成分和结构单元。有机物中原 子和结构单元的等张比容见表3-3。 子和结构单元的等张比容见表 。 某一有机物的[P] 可由下式计算： 可由下式计算： 某一有机物的 [P] =Σ[P]原子+Σ[P]结构单元 当温度远离临界温度时， 当温度远离临界温度时，ρ–ρ0 →ρ 上式可简化为： 上式可简化为：
五、化学组分影响
[P]的物理意义：在表面张力γ =1的温度下，液体摩尔体积即为等张比容。 的物理意义： 的温度下， 等张比容。 的物理意义 的温度下 液体摩尔体积即为等张比容
已知20℃ 戊烯的密度为0.640, 试求：1-戊烯的表面张力 。 试求： 戊烯的表面张力 戊烯的表面张力γ 例题 已知 ℃时1-戊烯的密度为 戊烯的密度为 例题 有机物等张比容计算 先求等张比容： 解： 先求等张比容： [P] =Σ[P] 原子+Σ[P]结构单元 = 5 [P] C+10 [P] H+ [P] = +10 [P]– =5x 9 +10x15. 5 +19 –10x 9. 5 =124 [实测值 123.8] 实测值
σ = F/ 2 • l
(1-9)
由上式可见，表面能又是作用在单位长度上液体表面的收缩力， 由上式可见，表面能又是作用在单位长度上液体表面的收缩力，这种力称 为表面张力（γ） 表面张力（ 物理学的定义：沿液体表面垂直作用于单位长度上的紧缩力。 γ物理学的定义：沿液体表面垂直作用于单位长度上的紧缩力。 表面张力的方向 和液体表面相切；和净吸力垂直。 和液体表面相切；和净吸力垂直。 20℃时常见液体表面张力（见表1.1） 20℃时常见液体表面张力（见表1.1） 1.1
分别为液体 液体a 液体b在相互饱和时的表面张力。 式中 γa ,γb --分别为液体a和液体b在相互饱和时的表面张力。 规则的验证： 作 Antonow 规则的验证：
二、相界面性质
其中: 苯 水 (实测值 实测值34.4) 其中: γ苯/水 = |γ水 - γ苯| = 63.2 - 28.8 = 34.4 (实测值34.4) 水 苯 由表中数据可见， 要小很多。 由表中数据可见，界面张力比表面张力γ要小很多。 戊醇/ 降到4. 其中最突出的是戊醇 水的界面张力降到 其中最突出的是戊醇/水的界面张力降到 8 mN/m.
§2-1 表面能与表面张力 一、表面能
2、一种表面两组分体系 、
一、表面能 两组分组成， 恒定时，体系的表面能的定义 若体系由 m和n两组分组成，当组分 n 恒定时，体系的表面能的定义 和 两组分组成
式：
σ=（δG /δA）T.P, n （1-5） （ ） ）
物理意义：在恒温、恒压和恒组分 的条件下 的条件下， 物理意义：在恒温、恒压和恒组分n的条件下，可逆的变化单位表面 积所引起的体系自由能变化量。 积所引起的体系自由能变化量。 由此可见，体系的表面能不但与温度压力有关， 由此可见，体系的表面能不但与温度压力有关，而且随体系中组分的 改变而改变。 改变而改变。
表1.1 一些纯液体的表面张力
从表中数据可见： 从表中数据可见： Hg的 最大485.5 水是次之。 485.5， ① 常见纯液体中 Hg的γ值最大485.5，水是次之。 ② 有机液体 表面张力在50～60mN/m， 且γ极性 >γ非极性 表面张力在 ～ ，
§2-2 影响表面张力的因素
一、物质本性（分子间吸引力） 物质本性影响表面张力的因素 液体分子间的吸引力↗， σ值↗ 液体分子间的吸引力↗ §2-2 （分子间吸引力） 液体名称： 液态Cu(1100 Cu(1100℃ 液体名称： 水 正己烷 Hg 液态Cu(1100℃) 一、物质本性 二、相界面性质 ： N/m） γ值（m N/m） 72.75 18.4 485 879 二、相界面性质 当两种液体接触时，其界面张力γa/ b 可用安东诺夫（Antonow）规 当两种液体接触时，其界面张力 可用安东诺夫（Antonow） 则计算： 则计算：
3、多种界面多组分体系 、
表面能的定义式： 表面能的定义式： σi =（δG /δA）T.P, ni, Aj≠i （1-6） （ ） ） 物理意义:在恒温、恒压和恒组分n的条件下，可逆的变化第i 种单位 物理意义 在恒温、恒压和恒组分 的条件下，可逆的变化第 在恒温 的条件下 界面所引起的体系自由能变化量。 界面所引起的体系自由能变化量。
Antonow 规则的验证
三、温度影响 体系的温度↗ 分子间引力↙ 体系的温度↗；分子间引力↙； γ↙（图1-3）。 当温度升高接近液体临界温度( 近似等于沸点) 当温度升高接近液体临界温度(tc 近似等于沸点) 时，液-气界面逐渐消失，此时γ→0。 气界面逐渐消失，
γ- t 的经验关系式： 的经验关系式：
三、温度影响 三、温度影响 三、温度影响 三、温度影响
约特弗斯(Eötvös)公式： (Eötvös)公式 ① 约特弗斯(Eötvös)公式： γVm2/3 =k (tc -t)
表1.2 温度对液体表面张力的影响
四、压力影响 通常， ↗; 影响不大； 通常，p↗; 对γ影响不大； 例如：20℃ 例如：20℃ 1atm σH2O = 72.75 ; σCCl4 = 26.8 四、压力影响 10atm σH2O = 71.75 ; σCCl4 = 25.8 在热力学上可以导出如下公式： 在热力学上可以导出如下公式：
∵
∴γ={ρ[P] /M }4 = { 124 x 0.64/70 }4 = 1. 65
§2-3 弯曲液面现象
§2-3 一、弯曲液面下附加压力(Δ弯曲液面现象 弯曲液面下附加压力( P)
1、凸液面 由于液体的表面张力总是力图收缩 液体的体积， 液体的体积，∴液体表面产生向着液体 内部的附加压力Δ 其数值为液面内、 内部的附加压力ΔP，其数值为液面内、 外压力之差， 外压力之差， 即：ΔP = P凸液 - P气, 且ΔP > 0 2、凹液面 如图1 4(b)所示 如图1-4(b)所示 ∴ P凹液 < P气 此时 ΔP< 0 凹液面内的附加压力与凸液面正好相反，附加压力Δ 凹液面内的附加压力与凸液面正好相反，附加压力ΔP = P凹液- P气 ，由于 液面内的压力有使凹面变成平面的趋势， 液面内的压力有使凹面变成平面的趋势， 结论: 结论: 附加压力Δ 的方向总是指向曲率中心； (1) 附加压力ΔP的方向总是指向曲率中心； 向着曲率中心一侧的压力总是比弯曲液面另一侧压力大。 (2) 向着曲率中心一侧的压力总是比弯曲液面另一侧压力大。 3、平液面 由于表面张力沿着平面作用，表面收缩力向四方展开并相互抵消， 由于表面张力沿着平面作用，表面收缩力向四方展开并相互抵消，∴ΔP = 0 如图1 4(a)所示 如图1-4(a)所示 一、弯曲液面下附加压力(ΔP) 弯曲液面下附加压力(