连续体的振动
第四章 连续体的振动

第四章连续体的振动拉格朗日(grange):1762年建立了离散系统振动的一般理论.对连续系统研究最早的是弦线的振动达朗贝尔(J.le R.d’Alembert)1746年用偏微分方程得到弦线振动的波动方程,并求出行波解伯努利(D.Bernoulli)1753年用无穷多个模态叠加的方法得到了弦线振动的驻波解1759年拉格朗日(grange):从驻波解推得行波解1811年傅里叶提出函数的阶数展开理论,给出严格的数学证明‘其它连续系统的振动问题也相继得到研究伯努利(D.Bernoulli)1744-1751年研究了梁的横向振动,导出了自由.简支和固定端的频率方程和振型函数奇拉尼(E.F.F.Chladni):1802年研究了杆的轴向和扭转振动.本章只讨论理想弹性体的振动理想弹塑性体满足以下假设条件①各向同性;②均质分布;③服从虎克定律§4.1 弦的振动T (,)q x t 讨论两端受到张力拉紧的弦,弦上还受到横向干扰力的作用(,)q x t yxdxxdm Adsρ=第四章连续体的振动设弦的密度为ρ(质量/单位体积)假设小变形,弦力不随挠度变化。
则弦上的任意一点的位移y 应为位置x 与时间t 的函数,即(,)y y x t =22()()dm Ads A dx dy Adxρρρ==+≈(,)(,)y x t x t tg xθθ∂=≈∂y [,]x x dx +沿方向作用在微小区间的外力之和为(,)[(,)](,)(,)(,)(,)x t T x t dx T x t q x t dxxx t T dx q x t dxxθθθθ∂+-+∂∂=+∂根据牛顿第二定律,弦的单元微段ds 沿y 方向的运动微分方程为:22(,)(,)(,)y x t x t Adx T dx q x t dx txθρ∂∂=+∂∂(,)(,)y x t x t xθ∂=∂代入得:2222(,)(,)(,)y x t y x t A T q x t t xρ∂∂=+∂∂22222(,)(,)1(,)y x t y x t c q x t t x Aρ∂∂=+∂∂Tc A ρ=设代入得:C 为波沿长度方向的传播速度(,)()()()sin()n y x t Y x H t Y x t ωϕ==+如无干扰力作用时,22222(,)(,)y x t y x t c t x∂∂=∂∂——称为波动方程弹性体系统作某阶主振动时,其各点也应当作同样的频率及相位运动,各点也应当同时通过静平衡位置和到达最大偏离位置,即系统具有一定的与时间无关的振型()Y x 为振型函数2222222(,)()sin()(,)()sin()nn n y x t Y x t t y x t d Y x t xdx ωωϕωϕ⎧∂=-+⎪⎪∂⎨∂⎪=+⎪∂⎩得2222()()sin()sin()n n n d Y x Y x t c t dx ωωϕωϕ-+=+()sincosnnY x A x B xc c ωω=+(,)(sin cos )sin()n nn y x t A x B x t c cωωωϕ=+⋅+2222()()0n d Y x Y x dxcω+=故,,,n A B ωϕ4个待定常数,可由弦的边界条件及振动的两个初始条件来确定。
第十二次课第四章连续体的振动

第四章连续体的振动§4.2 杆的纵向振动例:有一根 x =0 端为自由、x =l 端处为固定的杆,固定端承受支撑运动 td t u g ωsin )(=d 为振动的幅值试求杆的稳态响应。
l x 0)(t u g §4.2 杆的纵向振动解: l x 0t d t u g ωsin )(=方程建立 dx u dx x u u u g ∂-∂+)(22xu Sdx ∂∂ρdx x F F ∂∂+F 微段分析应变: xu u dx u dx x u u u g g ∂-∂=-∂-∂+=)(])([ε内力: xu u ES ES F g ∂-∂==)(ε达朗贝尔原理: F dx F F u Sdx -∂+=∂)(2ρ),(t x u 杆上距原点 x 处截面在时刻 t 的纵向位移 22)(u u ES u S g -∂=∂ρl x 0td t u g ωsin )(=令: 代入方程: 2222)(x u u ES t u S g ∂-∂=∂∂ρg u u u -=*g u u u +=*即: **''g Su ESu Su ρρ-=-2sin Sd tρωω=-设解为: ∑∞==1*)()(i i i t q x u φ)(x i φ为归一化的正则模态 ,...5,3,1,2cos 2)(==i x li l x i πφ代入方程,得: tSd ESq q S i i i i i ωωρφφρsin )(2,...5,3,1''=-∑∞=l x0t d t u g ωsin )(=2222)(x u u ES t u S g ∂-∂=∂∂ρgu u u -=*∑∞==1*)()(i i i t q x u φ,...5,3,1,2cos 2)(==i x l i l x i πφtSd ESq q S i i i i i ωωρφφρsin )(2,...5,3,1''=-∑∞= )(x j φ用 乘上式,并沿杆长积分:⎰∑⎰⎰=-∞=lj i l j i i l j i idx t Sd dx ES q dx S q 0210''0sin )(φωωρφφφφρ 利用正交性: t d i l l q q i i i i ωωπωsin )1(2222/)1(2--=+l x 0td t u g ωsin )(=2222)(x u u ES t u S g ∂-∂=∂∂ρg u u u -=*∑∞==1*)()(i i i t q x u φ,...5,3,1,2cos 2)(==i x li l x i πφt d i l l q q i i i i ωωπωsin )1(2222/)1(2--=+ 模态稳态解: t d i l l q i i i i ωπηωωsin )1(222/)1(22--=2)/(11i i ωωη-=t lx i d i E l u i i i ωπηπωρsin 2cos )1(16,...5,3,132/)1(322*∑∞=--=l x 0td t u g ωsin )(=2222)(x u u ES t u S g ∂-∂=∂∂ρg u u u -=*2)/(11i i ωωη-=t lx i d i E l u i i i ωπηπωρsin 2cos )1(16,...5,3,132/)1(322*∑∞=--=t d l x i i E l u u u i i i gωπηπωρsin 2cos )1(161 ,...5,3,12/)1(3322*⎥⎦⎤⎢⎣⎡-+=+=∑∞=-小结1. 建立动力学方程2. 根据边界条件求解固有频率和模态3. 变量分离4. 代入动力学方程,并利用正交性条件得到模态空间方程5. 物理空间初始条件转到模态空间6. 模态空间方程求解7. 返回物理空间,得解)()(),(1t q x t x u i i i φ∞=∑=)(2t Q q q j j j j =+ω )(,x i i φω)0(),0(j j q q )(t q j )()(),(1t q x t x u i i i φ∞=∑=物理空间问题 模态空间问题 )()(),(1t q x t x u i i i φ∞=∑=模态叠加法§4.3圆轴的扭转振动取圆轴的轴心线作为x 轴,图示轴任一 x 截面处的转角表示为θ(x ,t ) 。
第七章弹性连续体振动的准确解
179第七章 弹性连续体振动的准确解实际的振系都是弹性连续体系统,在很多情况下只是为了使问题简化,计算简便,才把它们简化成前几章所讨论的有限多的离散系统来分析。
当需要对弹性体振动问题作严密的分析时,这时就需要作为连续系统来处理。
弹性连续体问题与离散体问题有不同的特点,弹性连续体的质量、刚度、阻尼是连续分布的,因之具有无限多个自由度,需用无限多个点的独立坐标来表确定,其运动微分方程需要用偏微分方程来描述,而离散体在力学模型上具有明显的集中质量和不计质量的弹性元件,其自由度有限,运动以与自由度个数相等的二阶常系数微分方程来描述。
尽管如此,但两类问题在物理本质上是相同的,若把连续系统的质量分段聚集到有限个点上,各点之间用弹性元件连接起来便成为连续体,反之,离散系统当其质点数趋于无限多时就成为连续体,它们之间有相同的动力特性。
n 自由度连续体系统有n 个固有频率及主振型,而连续体则有无限多个固有频率及主振型,连续体中也存在各个主振型之间关于质量矩阵、刚度矩阵的正交性,对弹性体的响应分析,主振型迭加法有效。
本章将研究具有以下三个条件的理想弹性连续体振动问题的求解:1.材料是均匀的,具有各向同性;2.应力不超过弹性极限、并服从虎克定律;3.变形是微小的且是连续的。
具体是一维弹性体:轴、杆、梁等。
至于其它类弹性连续体如板、壳等的振动问题,因涉及到弹性力学知识,本章将不予讨论。
7-1弦的横向振动先研究最简单的弦的横向振动问题。
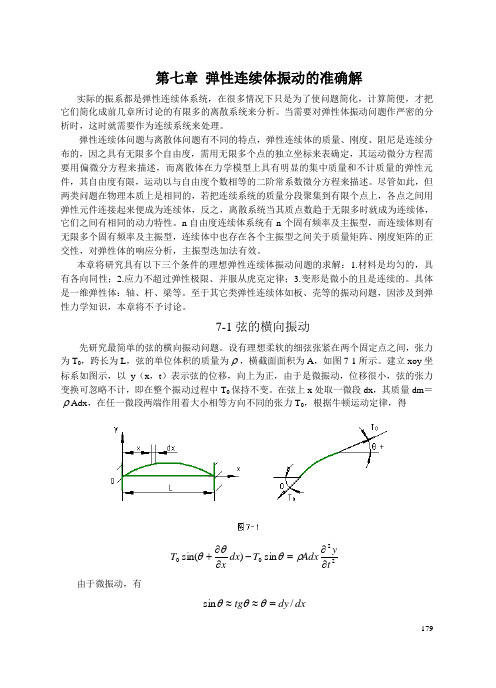
设有理想柔软的细弦张紧在两个固定点之间,张力为T 0,跨长为L ,弦的单位体积的质量为ρ,橫截面面积为A ,如图7-1所示。
建立xoy 坐标系如图示,以y (x ,t )表示弦的位移,向上为正,由于是微振动,位移很小,弦的张力变换可忽略不计,即在整个振动过程中T 0保持不变。
在弦上x 处取一微段dx ,其质量dm =ρAdx ,在任一微段两端作用着大小相等方向不同的张力T 0,根据牛顿运动定律,得2200sin )sin(tyAdx T dx x T ∂∂=-∂∂+ρθθθ由于微振动,有dx dy tg /sin =≈≈θθθ180故有2200)(ty Adx T dx x T ∂∂=-∂∂+ρθθθ代入x y∂∂=θ,简化后,即为 22220ty A x y T ∂∂=∂∂ρ 或写成22222t y a x y ∂∂=∂∂ (7-1) 式中AT a ρ0=称为波沿弦长度方向传播的速度。
无限自由度体系振动(第15讲,11月23日)

=0
频率方程
cos λl cosh λl +1= 0
解得: 解得: 当 i=1,2,3时 λ1l =1.875 时
λ2l = 4.694
λ3l = 7.855
2i −1 当 i ≥ 3时 λil ≈ π , (i = 3,4,⋯ ) 2 EI 2 各阶固有频率: ωi = (λil) 各阶固有频率: , (i =1,2,⋯ ) 4 ρSl
0
y
x
φ(0) = 0 φ′′(0) = 0 φ(l) = 0 φ′′(l) = 0
A =0 4
A = A =0 1 3 A sin λl + A sinh λl = 0 2 4 −A sin λl + A sinh λl = 0 2 4
频率方程: 频率方程: sin λl = 0
iπ 2 EI , (i = 1,2,⋯ ) 固有频率: 固有频率: ωi = ( ) l ρS ω2 2 EI 4 ϕ(x) = A cos λx + A2 sin λx + A3 cosh λx + A4 sinh λx λ = 2 a0 = 1 a0 ρS
再来看空间方程
ϕ '''' ( x ) − λ ϕ ( x ) = 0
4
假定解的形式为: 假定解的形式为:
ϕ ( x ) = De
由此可得: 由此可得:
αx
α = ± λ , ± iλ
无限自由度体系的振动 / 单跨梁的横向弯曲自由振动
于是可得: 于是可得:
ϕ ( x ) = D1eiλ x + D2e −iλ x + D3eλ x + D4 e− λ x
无限自由度体系的振动 / 单跨梁的横向弯曲自由振动
连续系统振动(a)-杆的纵向振动

2015年1月24 日 并考虑到: 《振动力学》
2 y 达朗贝尔 Adx 2 t 惯性力
y x
2 2 y 1 2 y a p ( x, t ) 弦的横向强迫振动方程 0 2 2 t x
a0 弹性横波的纵向传播速度
9
连续系统的振动 / 一维波动方程
( l ) 0 l cos 0 a0
u (l , t ) 0 x
频率方程
零固有频率对应的常值模态为杆的纵向刚性位移 x x 2015年1月24日 u ( x , t ) ( x ) q (t ) ( x ) c1 sin c2 cos 《振动力学》 a0 a0
2015年1月24日 《振动力学》
( x) (t ) q 2 a0 (常数) q(t ) ( x)
13
连续系统的振动 / 杆的纵向振动 记: 2
(t ) q 2 ( x) a0 q(t ) ( x)
''
q (t ) 2 q (t ) 0 2 ( x) ( a ) ( x) 0 0
i 1
2015年1月24日 《振动力学》 15
连续系统的振动 / 杆的纵向振动
几种常见边界条件下的固有频率和模态函数
(1)两端固定 特征:两端位移为零 边界条件: u(0, t ) (0)q(t ) 0
0 l
x
u(l , t ) (l )q(t ) 0
q(t )
不能恒为零
u ( x , t ) ( x ) q (t ) 19
连续系统的振动 / 杆的纵向振动
0 l
x
0 l
x
第十三次课第四章连续体的振动

§4.4 梁的弯曲振动
C1 (cos l cosh l ) C2 (sin l sinh l ) 0 C1 (cos l cosh l ) C2 (sin l sinh l ) 0
cos l cosh l C1、C2 非零解条件: sin l sinh l
(3)
分部积分 : j dx 0 j (EIi)dx j (EIi) 0 j (EIi) 0 0 EIi dx (4) (EI )dx EI dx S dx (5) 代入(3)式,有 : EI dx S dx 同理, (2)式两边乘 i 并沿梁长积分可得: EI l
y
0
x
解得: 当 i 0 时
2 模态函数: i ( x) cos i x cosh i x i (sin i x sinh i x), (i 1,2,)
其中: i
0l 0 对应刚体模态 当 i=1,2,3时 1l 4.730 2l 7.853 3l 10.996 1 i 3 当 时 i l (i ) , (i 3,4,)
y ( x, t ) ( x)q (t )
固定端: (0) 0
y
(0) 0
0
k1
弹性支撑端: EI (l ) k2 (l ) EI (l ) k1 (l )
k2
l
x
由固定端条件解得:C1 C3 , C2 C4 由弹性支撑固定端条件解得:
4
2
2 a0
EI a S
2 0
§4.4 梁的弯曲振动
y
(0) 0
第七章 连续体振动讲诉

五、超声波的特点(2)
• 容易衰减(在液体和固体中衰减较小) • 传播速度受温度影响 • 在两种不同介质的界面处反射强烈,在 许多场合必须使用耦合剂或匹配材料。 • 超声波可以聚焦。
六、超声波的产生机制
• • • • • 电磁振动 磁致伸缩效应 压电效应 静电引力 其它形式的机械振动
超声波效应
梁的弯曲振动方程为:
梁弯曲振动方程的解的一般形式就可以表示成:
对于两端固定的梁,其固定边界处位移为零,同 时位移曲 线在边界处的斜率也为零,因此 :
其特征值方程为:
其解αl不能解析表达出来,但当n>3时,可近似表达为:
梁弯曲振动的固有频率为 n
两端自由梁,弯曲振动的边界条件为:
超声波的类型
• • • • 纵波 横波 表面波 板波
纵波 横波 超声波分 类 表面波 板波 超声波在均匀介质中传播
纵波:质点振动方向 和波的传播方向在同 一条直线上的传播的 波称为纵波。也称压 缩波或疏密波。
一、超声波分类
横波:质点振动方向和波的传播方向相垂直的波称为横纵波。也 称切变波。横波只能在固体材料中传播。
由于液体和气体介质没有刚性,不能承受切应力,横波和表面波不能在 液体和气体中传播,只有纵波可以在液体气体中传播。
三、超声波声速
纵波在液体气体 中声速
C K
结论: 1、介质弹性性能愈强(E越大),密度愈小,则超声波在该介质中传 播声速愈高; 2、在同一种介质中,纵波声速约为横波的2倍,横波声速约为表面波0,9 倍; 3、在液体和气体介质中只能传播纵波。
四、超声波传播时相遇
4、惠更斯原理 在连续介质中传播波的波前所有各点, 都可以看作是发射子波的波源,经过 一段时间后,这些子波波前新位置的 包络线决定新的波阵面。这就是惠更 斯原理。
连续系统的振动 振动力学课件

(l )q(t )
C1
sin
l
a
2 q(t )
q(t) A cos(t )
q(t) A2 sin(t ) 2q(t)
2u t 2
(l)q(t)
C1 sin
l
a
2 q(t )
代入
EA u(l,t) W x g
2u(l, t 2
t
)
ku(l
,
t
)
0
2
EA cos l q t W 2 sin l q t k sin l q t 0
u(x, 0) u(x) u(x, 0) u(x) 确定
2.两端自由
特征:两自由端轴向力为零
即 FN (0,t) 0 FN (l,t) 0
EA u(0,t) 0, x
EA u(l,t) 0, x
'(0)qt 0
'(l)qt 0
' (0) 0
' (l) 0
2.两端自由
' (x)
W gkl 2
Eg
EA kl
W
lA
tan
a
l
EA
a
W 2 k
g
EA ( l)
lk a
Wa2 gkl 2
a
l
2
1
l
a
( l)2
a
1
讨论:(1)
W 0 右端只有弹簧k,
频率方程
tan l (l )
a
a
tanu u作图法得出
(2) W 0 k 0 即自由端情形
频率方程 cos l 0
2. 弹性弦横向振动
微段分析
以变形前弦的方向为 x轴,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
轴的扭转振动
所以根据弦横向振动微分方程的解可直接写出:
梁的横向振动
梁的横向自由振动 一根棱柱形梁在x-y平面内所做的横向自由振动
梁的横向振动
取微段
由达朗贝尔原理列出方程式:
梁的横向振动
化简得: (4-56) 对x+dx截面任一点取矩,做力矩平衡方程得:
化简得:
梁的横向振动
(4-57)
(4-58)
固有频率和主振型 从前面的章节中,我们知道振动系统的固有频率和主振型可以通 过研究其自由振动来获得。
弦的自由振动有一个性质:弦上的各点做同步运动
可以用数学中的分离变量法:将弦振动函数y(x,t)分解为空间函 数Y(x)和时间函数F(t)的乘积
弦的横向振动的固有频率和主振型
整理则有: (4-4)
(4-5)
由于弦各阶主振动的叠加即为自由振动定解,所以:
弦振动性结论
弦振动性结论 1.两端固定弦的自由振动,除了基频之外,还可以包含频率为 基频整数倍的振动,这种倍频振动称为谐波振动。在音乐上, 正是这种频率之间的整数倍关系模式的谐波与基波组成了各种 悦耳的谐音结构。 2.与离散系统相似,弦在任意初始条件下的自由振动可以由固 有振型的叠加构成。 3.阶数越高,节点数越越多。第i阶振型中节点个数为i-1。
连续体振动
关于连续体 咱们之前研究的单自由度、双自由度、多自由度系统 都是有限多自由度系统,可以看成由有限个质量、刚度 集中点所构成; 而连续体则将零件看成由质量、刚度连续分布的物体所 组成。 1.连续体也叫弹性体,具有连续分布的质量和弹性,现 实中的机械零件都是连续体。 2.由于确定连续体上无数质点的位置,需要无限多个坐 标,所以连续体是一种无限自由度的系统。 3.因连续体有无限个自由度,所以运动方程不再像有限 多自由度系统那样是二阶常微分方程组,而是偏微分方程
杆的纵向振动
以等截面细直杆的纵向振动为例
假设振动过程中各截面仍保持为平面 忽略有纵向振动引起的横向变形
杆的纵向振动
微段分析
u(x,t)为杆上距原点x处截面在时刻t的纵向位移
(4-36)
由达朗贝尔原理列出方程式为:
杆的纵向振动
(4-37)
将(3-35)代入(4-37)得:
(杆的纵向强迫振动方程)
关于方程(4-4)二阶常微分方程,解为: (4-6)
弦的横向振动的固有频率和主振型
式中,A、B由两个初始条件决定。
(4-7) 式中,C、D由两个初始条件决定。 对于两端固定的弦,边界条件是:
{
或
{
(4-8)
弦的横向振动的固有频率和主振型
运动的初始条件为:
{
(4-9)
有了这四个约束条件,就能求解系统的偏微分方程了。将(4-8) 代入式(4-7)中,得到:
轴的扭转振动
细长圆截面等直杆在分布扭矩作用下作扭转振动
假设振动过程中各截面仍保持为平面
轴的扭转振动
取微段,截面处的扭矩为T,则:
由达朗贝尔原理列出方程为:
整理得:
(圆截面杆的强迫振动方程)
轴的扭转振动
总结 弦的横向振动 杆的纵向振动
轴的扭转振动
虽然它们在运动形式上表现不同,但运动微分方程是类似的,都 是一维波动方程
薄膜的横向振动
如果外力f(x,y,t)=0,则可以由上式得自由振动方程:
(经典的二维波动方程)
对于等直杆ES为常数,自由振动时p(x,t)=0,所以:
杆的固有频率和主振型
由于杆的振动方程和弦横向振动方程类似,也是运用分离变 量法 u(x,t)=U(x)F(t) 式中 U(x)为空间函数,F(t)为时间函数 将上式代入(4-37)得:
设为
得到:
杆的纵向振动
这两个微分方程的解分别为:
轴的扭转振动
弦的横向振动
微元法求弦振动方程
弦两端固定,以张力F拉紧,在分布力作用下做横向振动 ρ为单位长度弦的质量 p(x,t)为单位长度弦上分布的作用力, 建立坐标系xoy y(x,t)弦上距原点x处的横截面在t时刻的横向位移
取微段,对微段进行受力分析:
弦的横向振动
根据达朗贝尔原理:
将方程整理得:
弦的横向振动的固有频率和主振型
(4-10)
这就是两端固定弦的特征方程,由此可得到一系列的特征值:
弦的横向振动的固有频率和主振型
(4-12)
一一对应
弦的横向振动的固有频率和主振型
由于D=0,振型是各点振幅的比值,比例因子C不影响该比值,所以: (4-13)
将(4-13)和(4-6)代入y(x,t)=Y(x)F(t)中,即得到弦的主振动
将(4-58)代入(4-56)得:
梁的横向振动
上式即为等截面横梁自由振动的运动方程,它是一个四阶齐次 偏微分方程
薄膜的横向振动
横向振动方程 如下图所示,在xy平面内边界曲线为S=S(x,y)的薄膜。 令f(x,y,t)表示沿z方向作用的力 T表示在某点处张力的密度,为常量
薄膜的横向振动
若薄膜均匀,载荷处处相等,则上式化简即获得薄膜横向 强迫振动的微分方程:
