初中数学几何-典型问题中的对角互补模型
全等与相似模型-对角互补模型(学生版)-2024年中考数学常见几何模型

全等与相似模型-对角互补模型全等三角形与相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就对角互补模型进行梳理及对应试题分析,方便掌握。
模型1、旋转中的对角互补模型对角互补模型概念:对角互补模型特指四边形中,存在一对对角互补,而且有一组邻边相等的几何模型。
思想方法:解决此类问题常用的辅助线画法主要有两种:①过顶点做双垂线,构造全等三角形;②进行旋转的构造,构造手拉手全等。
常见的对角互补模型含90°-90°对角互补模型、120°-60°对角互补模型、2α-(180°-2α)对角互补模型。
1)“共斜边等腰直角三角形+直角三角形”模型(异侧型)条件:如图,已知∠AOB=∠DCE=90°,OC平分∠AOB.结论:①CD=CE,②OD+OE=2OC,③S ODCE=S△COE+S△COD=12OC2.2)“斜边等腰直角三角形+直角三角形”模型(同侧型)条件:如图,已知∠DCE的一边与AO的延长线交于点D,∠AOB=∠DCE=90°,OC平分∠AOB.结论:①CD=CE,②OE-OD=2OC,③S△COE-S△COD=12OC2.3)“等边三角形对120°模型”(1)条件:如图,已知∠AOB=2∠DCE=120°,OC平分∠AOB.结论:①CD=CE,②OD+OE=OC,③S△COD+S△COE=34OC2.4)“等边三角形对120°模型”(2)条件:如图,已知∠AOB=2∠DCE=120°,OC平分∠AOB,∠DCE的一边与BO的延长线交于点D,结论:①CD=CE,②OD-OE=OC,③S△COD-S△COE=34OC2.5)“120°等腰三角形对60°模型”条件:△ABC是等腰三角形,且∠BAC=120°,∠BPC=60°。
专题 对角互补模型综合应用(知识解读)-中考数学(全国通用)

专题05 对角互补模型综合应用(知识解读)【专题说明】共顶点模型,即四边形或构成的几何图形中,相对的角互补。
主要:含90°的对角互补,含120°的对角互补,两种类型,种类不同,得出的个别结论会有所区别。
解决此类题型常用到的辅助线画法主要有两种:旋转法和过顶点作两垂线.【方法技巧】类型一:含90°的对角互补模型(1)如图,∠AOB=∠DCE=90°,OC平分∠AOB,则有以下结论:作法1 作法2;;(2)如图,∠AOB=∠DCE=90°,OC平分∠AOB,当∠DCE的一边与AO的延长线交于点D 时,则有以下结论:作法1 作法2;;类型二:含120°的对角互补模型(1)如图,∠AOB=2∠DCE=120°,OC平分∠AOB,则有以下结论:作法1 作法2;;(2)如图,∠AOB=∠DCE=90°,OC平分∠AOB,当∠DCE的一边与AO的延长线交于点D 时,则有以下结论:作法1 作法2;;【典例分析】【类型一:含90°的对角互补模型】【典例1】(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,线段EF、BE、FD之间的关系是;(不需要证明)(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD 上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.(3)如图3,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD 延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明.若不成立,请写出它们之间的数量关系,并证明.【变式1-1】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,连接EF交AP于点G,以下五个结论:①∠B=∠C=45°;②AP=EF;③∠AFP和∠AEP互补;④△EPF是等腰直角三角形;⑤四边形AEPF的面积是△ABC面积的,其中正确的结论是()A.①②③B.①②④⑤C.①③④⑤D.①③④【变式1-2】(1)如图1,在四边形ABCD中,AB=AD,∠BAD=100°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=50°.探究图中线段EF,BE,FD之间的数量关系.小明同学探究的方法是:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论是(直接写结论,不需证明);(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD 上的点,且2∠EAF=∠BAD,上述结论是否仍然成立,若成立,请证明,若不成立,请说明理由;(3)如图3,四边形ABCD是边长为7的正方形,∠EBF=45°,直接写出△DEF的周长.【变式1-3】(1)如图①,在四边形ABCD中,AB=AD,∠B=∠D=90°,E,F分别是边BC,CD上的点,且∠EAF=∠BAD.请直接写出线段EF,BE,FD之间的数量关系:;(2)如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD 上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?请写出证明过程;(3)在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD所在直线上的点,且∠EAF=∠BAD.请直接写出线段EF,BE,FD之间的数量关系:.【变式1-4】问题探究:如图1,在△ABC中,点D是BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.①BE、CF与EF之间的关系为:BE+CF EF;(填“>”、“=”或“<”)②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明.问题解决:如图2,在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=130°,以D为顶点作∠EDF=65°,∠EDF的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.【类型二:含120°的对角互补模型】【典例2】问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC =90°,E,F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD 之间的数量关系,小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以70海里/小时的速度前进,舰艇乙沿北偏东50°的方向以90海里/小时的速度,前进2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.【变式2-1】如图,△ABC是边长为6的等边三角形,BD=CD,∠BDC=120°,以点D 为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连结MN,则△AMN 的周长是.【变式2-2】【问题背景】如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,试探究图中线段BE、EF、FD之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE,连接AG,先证明△ABE ≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是.【探索延伸】如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由.【学以致用】如图3,四边形ABCD是边长为5的正方形,∠EBF=45°,直接写出△DEF的周长.专题05 对角互补模型综合应用(知识解读)【专题说明】共顶点模型,即四边形或构成的几何图形中,相对的角互补。
初中数学对角互补模型(初中数学最新最全对角互补模型)

二、对角互补双90°模型(构造相似)
例4.如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN,∠MPN=90°,点P在AC上,PM交AB 于点E,PN交BC于点F,当PE=2PF时,求AP
课堂练习
三、对角互补.60°、120°模型(构造全等)
例5.已知∠AOB=120°,OC平分∠AOB,点P是射线OC上一点. (1)如图1,过点P作PD⊥OA,PE⊥OB,说明PD与PE相等的理由;
(3)如图3所示,过C作CH⊥BD于H,BD=6,AD=3,求CH
(3)如图,过点C作CQ⊥CD交BD于点Q, ∵∠ACB=90°,QC⊥CD∴∠ACB=∠ADB=90°, ∴点A,点B,点C,点D四点共圆,∴∠CDQ=∠CAB=45°∵QC⊥CD ∴∠CQD=∠CDQ=45°∴CQ=CD,且∠QCD=90°∴△DCQ是等腰直角
(2)证明:过P作PE⊥BC,PF⊥CD, ∵P,C为正方形对角线AC上的点, ∴PC平分∠DCB,∠DCB=90°,∴PF=PE, ∴四边形PECF为正方形, ∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°, ∴∠BPE=∠QPF,∴Rt△PQF≌Rt△PBE,∴PB=PQ.
课堂练习
练习1.如图,正方形ABCD与正方形OMNP的边长均为10,点O是正方形ABCD的中心,正
方形OMNP绕O点旋转,这两个正方形重叠部分的面积为
.
练习2.如图,正方形ABCD的对角线AC与BD相交于点O,E,F分别是AB,BC上的 点,连接EF.若AE=4,CF=3,OE⊥OF,求EF的长.
练习3.如图,在平面直角坐标系中,正方形ABCD顶点A的坐标为(0,2),B点 在x轴上,对角线AC,BD交于点M,OM=3 ,求点B的坐标.
中考数学专项复习题型突破专题十 全等——对角互补模型

,与的面积相等,矩形 为正方形,则四边形的面积 正方形 的面积.由勾股定理得,,, ,即四边形 的面积为18.
例题解图
解法2:如解图②,将 绕点 顺时针旋转 得到 ,从而有等腰 , 四边形 的面积 等腰直角 的面积 .
例题解图
归纳总结
类型
双 对角互补
第2题解图
解法2:如解图②,过点 分别作 于点 ,作 于点 ,连接 , 是 的中点, 是 的平分线, , , , , , , , ,在 中, , , ,同理, , , , .
第2题解图
一、模型、方法篇
专题十 全等——对角互补模型
例题图
例 (多解法)如图,在四边形 中, , ,连接 ,若 ,则四边形 的面积为____.
18
【解析】解法1:如解图①,过点 作 于点 ,过点 作 交 的延长线于点 , 四边形 为矩形, , .在 与 中, ,
第1题图
证明: , ,在 和 中, , .
2.(多解法)如图,等边三角形 的边长为4, 是边 的中点, 在边 上, ,点 在边 的延长线上,且 ,则 的长为___.
1
第2题图
【解析】解法1:如解图①,过点 作 ,则 , , , 是 的中点, , , , , .
, 对角互补模型
图示
_
_
续表
旋转构等边三角形
作垂直构全等
旋转构等腰直角三角形
作垂直构全等
作法
类型
双 对角互补
,对角互补模型
结论
②四边形 是正方形
是等腰直角三角形,
是等边三角形
是等边三角形
续表
针对训练
第1题图
1.[2023大连]如图,在 和 中,延长 交 于 , , .求证: .
中考补充专题11.对角互补模型

专题11.“对角互补模型”一.知识点:1.如图,已知∠AO B +∠DCE =180°,且点C 在∠AOB 的平分线上. 结论:①CD =CE ;②∠AO B =90°时,OD +OE =2O C ; ③∠AO B =90°时,OD +OE =O C .2. 如图,已知∠AO B +∠DCE =180°. 结论:CE =CD ·tan ∠CGP3. 已知∠B AC =∠B DC =90°,AB =AC . 结论:B D +CD =2AD拓展:已知∠A BC =60°,∠ADC =120°,AB =,BC 结论:A D +DC =BD, S 四边形ABCD =S △ABD +S △BCD =43BD 2二.典型例题1.如图,AC 平分∠BAD ,∠B +∠D =180°,CE ⊥AD 于点E ,AD =12cm ,AB =7cm ,求DE 的长.2.如图在Rt △ABC 中,∠ABC =90°,∠A =30°,点P 是线段AC 的中点,点M 为线段AB 延长线上一点,点N 为线段BC 延长线上一点,且∠MPN =90°,求证:=33.3.已知△ABC是等边三角形,点D是AC的中点,点E在射线BC上,点F在射线BA上,∠EDF =120°.(1)如图1,若点F与B点重合,求证:DB=DE;(2)如图2,若点E在线段BC上,点F在线段BA 上,求的值;(3)如图3,若AF+CE=BD,直接写出∠EDC 的度数为.三.变式练习1.如图,△ABC为等边三角形,以AB为边向形外作△ABD,使∠ADB=120°,再以点C为旋转中心把△CBD旋转到△CAE,则下列结论:①D、A、E三点共线;②DC平分∠BDA;③∠E=∠BAC;④DC=DB+DA.其中正确的有()A.4个B.3个C.2个D.1个2.已知:正方形ABCD中,对角线AC、BD交于点O,过O点的两直线OE、OF互相垂直,分别交AB、BC于E、F,连接EF,若AE=4,CF=3,求EF 的长.3.如图,在等边△ABC,点O为三个内角平分线的交点,∠EOF=120°,交边BC、AC于E、F,求证:OE=OF;4.(1)【探究发现】如图1,∠EOF的顶点O在正方形ABCD两条对角线的交点处,∠EOF=90°,将∠EOF绕点O 旋转,旋转过程中,∠EOF的两边分别与正方形ABCD的边BC和CD交于点E和点F(点F与点C,D不重合).则CE,CF,BC之间满足的数量关系是.(2)【类比应用】如图2,若将(1)中的“正方形ABCD”改为“∠BCD=120°的菱形ABCD”,其他条件不变,当∠EOF=60°时,上述结论是否仍然成立?若成立,请给出证明;若不成立,请猜想结论并说明理由.(3)【拓展延伸】如图3,∠BOD=120°,OD =,OB=4,OA 平分∠BOD,AB=,且OB>2OA,点C是OB上一点,∠CAD=60°,求OC的长.5.如图,点D是等边△ABC外一点,且DB=DC,∠BDC=120°,将一个三角尺60°的顶点放在点D 上,三角尺的两边DP、DQ分别与射线AB、CA相交于E、F两点.(1)当EF∥BC时,如图①,证明:EF=BE+CF;(2)当三角尺绕点D旋转到如图②的位置时,线段EF、BE、CF之间的上述数量关系是否成立?如果成立,请给予证明;如果不成立,写出EF、BE、CF之间的数量关系,并说明理由;(3)当三角尺绕点D继续旋转到如图③的位置时,(1)中的结论是否发生变化?如果不变化,直接写出结论;如果变化,请直接写出EF、BE、CF之间的数量关系.【分析】(1)根据△ABC是等边三角形知道AB =AC,∠ABC=∠ACB=60°,而DB=DC,∠BDC =120°,这样可以得到△DCF和△BED 是直角三角形,由于EF∥BC,可以证明△AEF是等边三角形,也可以证明△BDE≌△CDF,可以得到DE=DF,由此进一步得到DE=DF∠BDE=∠CDF=30°,这样可以得到BE =DE =DF=CF,而△DEF是等边三角形,所以题目的结论就可以证明出来了;(2)结论仍然成立.如图,在AB的延长线上取点F′,使BF′=CF,连接DF′,根据(1)的结论可以证明△DCF≌△DBF′,根据全等三角形的性质可以得到DF=DF′,∠BDF′=∠CDF,又∠BDC=120°,∠EDF=60°,可以得到:∠EDF′=∠CDF=60°,由此可以证明△EDF′≌△EDF,从而证明题目的结论.(3)结论发生变化.EF=BE﹣CF.【解答】解:如图,点D是等边△ABC外一点,且DB=DC,∠BDC=120°,将一个三角尺60°的顶点放在点D上,角的两边分别为DP、DQ(1)证明:∵△ABC是等边三角形,∴AB=AC,∠ABC=∠ACB=60°.∵DB=DC,∠BDC=120°,∴∠DBC=∠DCB=30°.∴∠DBE=∠DBC+∠ABC=90°,∠DCF=∠DCB+∠ACB=90°,∵EF∥BC,∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°.∴AE=AF.∴BE=AB﹣AE=AC﹣AF=CF.又∵DB=DC,∠DBE=∠DCF,∴△BDE≌△CDF,∴DE=DF∠BDE=∠CDF=30°.∴BE=DE=DF=CF.∵∠EDF=60°,∴△DEF是等边三角形.即DE=DF=EF.∴BE+CF=DE+DF=EF.(2)结论仍然成立.证明:如图,在AB的延长线上取点F′,使BF′=CF,连接DF′.由(1)得,∠DBE=∠DCF=90°则∠DBF′=∠DCF=90°,又∵BD=CD,∴△DCF≌△DBF′(SAS)∴DF=DF′,∠BDF′=∠CDF,又∵∠BDC=120°,∠EDF=60°∴∠EDB+∠CDF=60°∴∠EDB+∠BDF′=∠EDF′=∠CDF=60°,又DE=DE,∴△EDF′≌△EDF(SAS).∴EF=EF′=BE+BF′=BE+CF.(3)结论发生变化.EF=CF﹣BE.。
初中数学几何模型之 对角互补模型
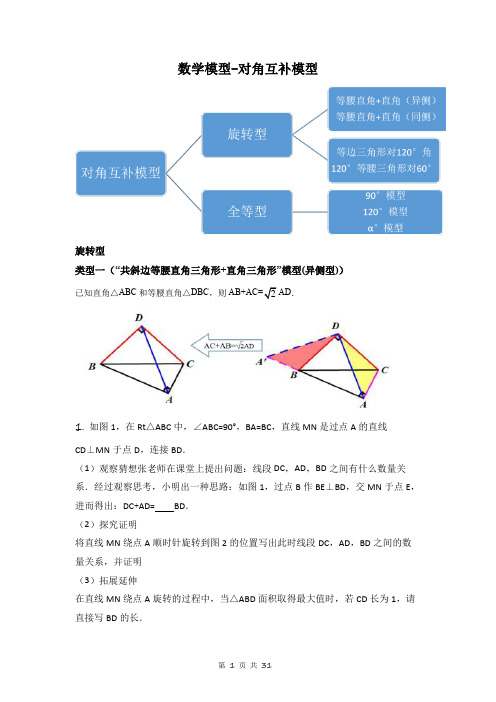
数学模型-对角互补模型旋转型类型一(“共斜边等腰直角三角形+直角三角形”模型(异侧型))已知直角△ABC和等腰直角△DBC,则AD.1. 如图1,在Rt△ABC中,∠ABC=90°,BA=BC,直线MN是过点A的直线CD⊥MN于点D,连接BD.(1)观察猜想张老师在课堂上提出问题:线段DC,AD,BD之间有什么数量关系.经过观察思考,小明出一种思路:如图1,过点B作BE⊥BD,交MN于点E,进而得出:DC+AD=BD.(2)探究证明将直线MN绕点A顺时针旋转到图2的位置写出此时线段DC,AD,BD之间的数量关系,并证明(3)拓展延伸在直线MN绕点A旋转的过程中,当△ABD面积取得最大值时,若CD长为1,请直接写BD的长.【答案】((2(AD ﹣;(3)+1.【解析】【分析】(1)根据全等三角形的性质求出DC(AD(BD 之间的数量关系 (2)过点B 作BE ⊥BD ,交MN 于点E(AD 交BC 于O(证明CDB AEB ∆∆≌,得到CD AE =(EB BD =,根据BED ∆为等腰直角三角形,得到DE =(再根据DE AD AE AD CD =-=-,即可解出答案.(3)根据A(B(C(D 四点共圆,得到当点D 在线段AB 的垂直平分线上且在AB 的右侧时,△ABD 的面积最大.在DA 上截取一点H ,使得CD=DH=1,则易证CH AH ==由BD AD =即可得出答案.【详解】解:(1)如图1中,由题意:BAE BCD ∆∆≌(∴AE=CD(BE=BD(∴CD+AD=AD+AE=DE(∵BDE ∆是等腰直角三角形,∴BD(∴((2(AD DC -=(证明:如图,过点B 作BE ⊥BD ,交MN 于点E(AD 交BC 于O(∵90ABC DBE ∠=∠=︒(∴ABE EBC CBD EBC ∠+∠=∠+∠(∴ABE CBD ∠=∠(∵90BAE AOB ∠+∠=︒(90BCD COD ∠+∠=︒(AOB COD ∠=∠(∴BAE BCD ∠=∠(∴ABE DBC ∠=∠.又∵AB CB =(∴CDB AEB ∆∆≌(∴CD AE =(EB BD =(∴BD ∆为等腰直角三角形,DE =(∵DE AD AE AD CD =-=-(∴AD DC -=((3)如图3中,易知A(B(C(D 四点共圆,当点D 在线段AB 的垂直平分线上且在AB 的右侧时,△ABD 的面积最大.此时DG⊥AB(DB=DA,在DA上截取一点H,使得CD=DH=1,则易证==CH AH∴1==(BD AD【点睛】本题主要考查全等三角形的性质,等腰直角三角形的性质以及图形的应用,正确作辅助线和熟悉图形特性是解题的关键.类型二(“共斜边等腰直角三角形+直角三角形”模型(同侧型))已知直角△ABC和等腰直角△DBC,则AD.2. 已知:△ABC中,CA=CB, ∠ACB=90º,D为△ABC外一点,且满足∠ADB=90º(1)如图所示,求证:DC(2)如图所示,猜想DA.DB.DC之间有何数量关系?并证明你的结论.(3)如图所示,过C作CH⊥BD于H,BD=6,AD=3,则CH= .【答案】(1)详见解析;(2);(3)3 2【解析】【分析】(1)过C点作CQ⊥CD交DB的延长线于Q点,由余角的性质可得∠ACD=∠QCB,∠ADC=∠Q,由“AAS”可证△ACD≌△BCQ,可得CD=CQ,AD=BQ,由等腰直角三角形性质可得DQ CD,即可得结论;(2)过点C作CQ⊥CD交AD于点Q,由“SAS”可证△ACQ≌△BCD,可得AQ=BD,可证CQ=CD,且∠QCD=90°,即可得DA、DB、DC之间关系;(3)过点C作CQ⊥CD交BD于点Q,由“SAS”可证△ACD≌△BCQ,可得AD=BQ,可证△DCQ是等腰直角三角形,由等腰直角三角形的性质可求CH的长.【详解】证明:(1)如图,过C点作CQ⊥CD交DB的延长线于Q点∵∠ACB=90°,CQ⊥CD,∠ADB=90°∴∠ACD+∠DCB=90°,∠DCB+∠QCB=90°,∠ADC+∠CDQ=90°,∠CDQ+∠Q=90°∴∠ACD=∠QCB,∠ADC=∠Q,且AC=BC∴△ACD≌△BCQ(AAS)∴CD=CQ,AD=BQ∴DQ=DB+BQ=DB+AD∵CD⊥CQ,∠DCQ=90°∴DQ∴DB+AD CD(2)DA-DB CD理由如下:如图,过点C作CQ⊥CD交AD于点Q,∵CA=CB,∠ACB=90°,∴∠ABC=∠CAB=45°∵∠ACB=90°,QC⊥CD∴∠ACB=∠ADB=90°,∴点A,点B,点D,点C四点共圆,∴∠ADC=∠ABC=45°∵QC⊥CD∴∠CQD=∠CDQ=45°∴CQ=CD,且∠QCD=90°∴QD CD∵∠ACB=∠DCQ=90°,∴∠ACQ=∠DCB,且AC=BC,CQ=CD∴△ACQ≌△BCD(SAS)∴AQ=BD∴QD=DA-AQ=DA-BD,即:DA-DB(3)如图,过点C作CQ⊥CD交BD于点Q,∵∠ACB=90°,QC⊥CD∴∠ACB=∠ADB=90°,∴点A,点B,点C,点D四点共圆,∴∠CDQ=∠CAB=45°∵QC⊥CD∴∠CQD=∠CDQ=45°∴CQ=CD,且∠QCD=90°∴△DCQ是等腰直角三角形,∵∠ACB=∠DCQ=90°,∴∠ACD=∠QCB,且AC=BC,CQ=CD∴△ACD≌△BCQ(SAS)∴AD=BQ,∴DQ=DB-BQ=DB-AD=3∵△DCQ是等腰直角三角形,DQ=3,CH⊥DB∴CH=DH=HQ=12DQ=32.故答案为32.【点睛】本题是三角形综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质,添加恰当辅助线构造全等三角形是本题的关键.类型三“等边三角形对120°模型”.△ABC是等边三角形,∠BPC=120°,则有PB+PC=PA;类型四“120°等腰三角形对60°模型”△ABC是等腰三角形,且∠BAC=120°,∠BPC=60°,则有;3. 例:截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长就是在长边上截取一条线段与某一短边相等,补短就是通过延长或旋转等方式使两条短边拼合到一起,从而解决问题.(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.解题思路:将△ABD绕点A逆时针旋转60°得到△ACE,可得AE=AD,CE=BD,∠ABD=∠ACE,∠DAE=60°,根据∠BAC+∠BDC=180°,可知∠ABD+∠ACD=180°,则∠ACE+∠ACD=180°,易知△ADE是等边三角形,所以AD=DE,从而解决问题.根据上述解题思路,三条线段DA、DB、DC之间的等量关系是___________;(2)如图2,Rt△ABC中,∠BAC=90°,AB=AC.点D是边BC下方一点,∠BDC=90°,探索三条线段DA、DB、DC之间的等量关系,并证明你的结论.【答案】(1)DA=DB+DC;(2) DA=DB+DC,证明见解析.【解析】【分析】(1)由旋转60°可得AE =AD , CE =BD ,∠ABD =∠ACE ,∠DAE =60°,根据∠BAC +∠BDC =180°,可知∠ABD +∠ACD =180°,则 ∠ACE +∠ACD =180°,易知△ADE 是等边三角形,所以AD =DE ,从而解决问题.(2) 延长DC 到点E,使CE=BD ,连接AE,由已知可得180ABD ACD ︒∠+∠=,根据180ACE ACD ︒∠+∠=,可得ABD ∠=ACE ∠,可证ABD ACE ≅,进而可得AD=AE, BAD CAE ∠=∠,可得90DAE BAC ︒∠=∠=,由勾股定理可得:222DA AE DE +=,进行等量代换可得结论.【详解】(1)结论:DA=DB+DC.理由:∵△ABD 绕点A 逆时针旋转60°得到△ACE ,∴AE=AD , CE=BD ,∠ABD=∠ACE ,∠DAE=60°,∵∠BAC+∠BDC=180°,∴∠ABD+∠ACD=180°,∴∠ACE+∠ACD=180°,∴D,C,E 三点共线,∵AE=AD ,∠DAE=60°,∴△ADE 是等边三角形,∴AD=DE ,∴AD=DC+CE=DB+DC;(2)证明如下:如图所示,延长DC 到点E,使CE=BD ,连接AE,∵90BAC ︒∠=,90BDC ︒∠=,∴180ABD ACD ︒∠+∠=,∵180ACE ACD ︒∠+∠=,∴ABD ∠=ACE ∠,∵AB=AC,CE=BD,∴ABD ACE ≅(SAS),∴AD=AE, BAD CAE ∠=∠,∴90DAE BAC ︒∠=∠=,∴222DA AE DE +=,∴()222DA DB DC =+,DA=DB+DC.【点睛】本题主要考查了截长补短的方法,通过全等三角形得到线段间的等量关系,正确作出辅助线找到全等三角形是解题的关键.4. 如图1,在四边形ABCD 中,AB=AD ,∠B+∠ADC=180°,点E ,F 分别在四边形ABCD 的边BC ,CD 上,∠EAF=12∠BAD ,连接EF ,试猜想EF ,BE ,DF 之间的数量关系.(1)思路梳理将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合,由∠B+∠ADC=180°,得∠FDG=180°,即点F,D,G三点共线,易证△AFG≌△AFE,故EF,BE,DF 之间的数量关系为__;(2)类比引申如图2,在图1的条件下,若点E,F由原来的位置分别变到四边形ABCD的边CB,DC延长线上,∠EAF=12∠BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并给出证明.(3)联想拓展如图3,在△ABC中,∠BAC=90°,AB=AC,点D,E均在边BC上,且∠DAE=45°,若BD=1,EC=2,直接写出DE的长为________________.【答案】(1)EF=BE+DF;(2)EF=DF−BE;证明见解析;(3【解析】【分析】(1)将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合,首先证明F,D,G三点共线,求出∠EAF=∠GAF,然后证明△AFG≌△AFE,根据全等三角形的性质解答;(2)将△ABE绕点A逆时针旋转,使AB与AD重合,得到△ADE',首先证明E',D,F三点共线,求出∠EAF=∠E'AF,然后证明△AFE≌△AFE',根据全等三角形的性质解答;(3)将△ABD绕点A逆时针旋转至△ACD',使AB与AC重合,连接ED',同(1)可证△AED≌AED',求出∠ECD'=90°,再根据勾股定理计算即可.【详解】解:(1)将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合,∵∠B+∠ADC=180°,∴∠FDG=180°,即点F,D,G三点共线,∵∠BAE=∠DAG,∠EAF=12∠BAD,∴∠EAF=∠GAF,在△AFG和△AFE中,AE AGEAF GAF AF AF⎧⎪∠∠⎨⎪⎩===,∴△AFG≌△AFE,∴EF=FG=DG+DF=BE+DF;(2)EF=DF−BE;证明:将△ABE绕点A逆时针旋转,使AB与AD重合,得到△ADE',则△ABE≌ADE',∴∠DAE'=∠BAE,AE'=AE,DE'=BE,∠ADE'=∠ABE,∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,∴∠ADE'=∠ADC,即E',D,F三点共线,∵∠EAF=12∠BAD,∴∠E'AF=∠BAD−(∠BAF+∠DAE')=∠BAD−(∠BAF+∠BAE)=∠BAD−∠EAF=12∠BAD,∴∠EAF=∠E'AF,在△AEF和△AE'F中,AE AEEAF E AF AF AF'⎧⎪∠∠'⎨⎪⎩===,∴△AFE≌△AFE'(SAS),∴FE=FE',又∵FE'=DF−DE',∴EF=DF−BE;(3)将△ABD绕点A逆时针旋转至△ACD',使AB与AC重合,连接ED',同(1)可证△AED≌AED',∴DE=D'E.∵∠ACB=∠B=∠ACD'=45°,∴∠ECD'=90°,在Rt△ECD'中,ED'2222'5D C EC BD,即DE【点睛】本题考查的是旋转变换的性质、全等三角形的判定和性质以及勾股定理等知识,灵活运用利用旋转变换作图、掌握全等三角形的判定定理和性质定理是解题的关键.构造全等型类型五-全等型90°条件:①∠AOB=∠DCE =90°,②OC平分∠AOB结论:①CD=CE;②OC;③S△DCE=S△OCD +S△OCE =12OC2辅助线的做法,可有下面两种方法来证明.当C与AO的延长线相交时,也是相同的方法.结论变:①CD=CE ;②OC ;③S △OCE - S △OCD =12OC 25. 探究:如图1和2,四边形ABCD 中,已知AB AD =,90BAD ∠=︒,点E ,F 分别在BC 、CD 上,45EAF ∠=︒.(1)①如图 1,若B 、ADC ∠都是直角,把ABE △绕点A 逆时针旋转90︒至ADG ,使AB 与AD 重合,则能证得EF BE DF =+,请写出推理过程; ②如图 2,若B 、D ∠都不是直角,则当B 与D ∠满足数量关系_______时,仍有EF BE DF =+;(2)拓展:如图3,在ABC 中,90BAC ∠=︒,AB AC ==D 、E 均在边BC 上,且45DAE ∠=︒.若1BD =,求DE 的长.【答案】(1)①见解析;②180B D ∠+∠=︒,理由见解析;(2)5=3DE 【解析】【分析】(1)①根据旋转的性质得出AE =AG ,∠BAE =∠DAG ,BE =DG ,求出∠EAF =∠GAF =45°,根据SAS 推出△EAF ≌△GAF ,根据全等三角形的性质得出EF =GF ,即可求出答案;②根据旋转的性质得出AE =AG ,∠B =∠ADG ,∠BAE =∠DAG ,求出C 、D 、G 在一条直线上,根据SAS 推出△EAF ≌△GAF ,根据全等三角形的性质得出EF =GF ,即可求出答案;(2)根据等腰直角三角形性质好勾股定理求出∠ABC =∠C =45°,BC =4,根据旋转的性质得出AF =AE ,∠FBA =∠C =45°,∠BAF =∠CAE ,求出∠FAD =∠DAE =45°,证△FAD ≌△EAD ,根据全等得出DF =DE ,设DE =x ,则DF =x ,BF =CE =3−x ,根据勾股定理得出方程,求出x 即可.【详解】(1)①如图1,∵把ABE △绕点A 逆时针旋转90︒至ADG ,使AB 与AD 重合,∴AE AG =,BAE DAG ∠=∠,BE DG =∵90BAD ∠=︒,45EAF ∠=︒,∴45BAE DAF ∠+∠=︒,∴45DAG DAF ∠+∠=︒,即45EAF GAF ∠=∠=︒,在EAF △和GAF 中AF AF EAF GAF AE AG =⎧⎪∠=∠⎨⎪=⎩∴()EAF GAF SAS ≌,∴EF GF =,∵BE DG =,∴EF GF BE DF ==+;②180B D ∠+∠=︒,理由是:把ABE △绕A 点旋转到ADG ,使AB 和AD 重合,则AE AG =,B ADG ∠=∠,BAE DAG ∠=∠,∵180B ADC ︒∠+∠=,∴180ADC ADG ∠+∠=︒,∴C ,D ,G 在一条直线上,和①知求法类似,45EAF GAF ∠=∠=︒,在EAF △和GAF 中AF AF EAF GAF AE AG =⎧⎪∠=∠⎨⎪=⎩∴()EAF GAF SAS △≌△,∴EF GF =,∵BE DG =,∴EF GF BE DF ==+;故答案为:180B D ∠+∠=︒(2)∵ABC中,AB AC ==90BAC ∠=∴45ABC C ∠=∠=︒,由勾股定理得:4BC === ,把AEC 绕A 点旋转到AFB △,使AB 和AC 重合,连接DF .则AF AE =,45FBA C ∠=∠=︒,BAF CAE ∠=∠,∵45DAE ∠=︒,∴904545FAD FAB BAD CAE BAD BAC DAE ∠=∠+∠=∠+∠=∠-∠=︒-︒=︒, ∴45FAD DAE ∠=∠=︒,在FAD △和EAD 中AD AD FAD EAD AF AE =⎧⎪∠=∠⎨⎪=⎩∴FAD EAD △≌△,∴DF DE =,设DE x =,则DF x =,∵1BC =,∴413BF CE x x ==--=-,∵45FBA ∠=︒,45ABC ∠=︒,∴90FBD ∠=︒,由勾股定理得:222DF BF BD =+,222(3)1x x =-+, 解得:5=3x , 即5=3DE . 【点睛】本题考查了旋转的性质,全等三角形的性质和判定,勾股定理的应用,此题是开放性试题,首先在特殊图形中找到规律,然后再推广到一般图形中,对学生的分析问题,解决问题的能力要求比较高.类型六-全等型120°条件:①∠AOB=2∠DCE =120°,②OC 平分∠AOB结论:①CD=CE ;②OD+OE=OC ;③S △DCE =S △OCD +S △OCE2证明提示:①可参考“全等型-90°”证法一;②如图:在OB 上取一点F ,使OF=OC ,证明△OCF 等边三角形.6. 如图,已知60AOB ∠=︒,在AOB ∠的角平分线OM 上有一点C ,将一个120︒角的顶点与点C 重合,它的两条边分别与射线,OA OB 相交于点,D E .(1)如图1,当DCE ∠绕点C 旋转到CD 与OA 垂直时,请猜想+OD OE 与OC 的数量关系,并说明理由;(2)当DCE ∠绕点C 旋转到CD 与OA 不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;(3)如图3,当DCE ∠绕点C 旋转到点D 位于OA 的反向延长线上时,求线段,OD OE 与OC 之间又有怎样的数量关系?请写出你的猜想,不需证明.【答案】(1)OD OE +=,见解析;(2)结论仍然成立,见解析;(3)OE OD -=【解析】【分析】(1)先判断出∠OCE =60°,再利用特殊角的三角函数得出OD ,同OE ,即可得出结论;(2)同(1)的方法得OF +OG ,再判断出△CFD ≌△CGE ,得出DF =EG ,最后等量代换即可得出结论;(3)同(2)的方法即可得出结论.【详解】解:(1)OM 是AOB ∠的角平分线1302AOC BOC AOB ∴∠=∠=∠=︒ ,90,60CD OA ODC OCD ⊥∴∠=︒∴∠=︒60OCE DCE OCD ∴∠=∠-∠=︒在Rt OCD ∆中,cos30OD OC =⋅︒=,同理:OE =OD OE ∴+=(2)(1)中结论仍然成立,理由:过点C 作CF OA ⊥于F ,CG OB ⊥于G90OFC OGC ∴∠=∠=︒60AOB ∠=︒120FCG ∴∠=︒由(1)知,,22OF OC OG ==OF OG ∴+=,CF OA CG OB ⊥⊥,且点C 是AOB ∠的平分线OM 上一点CF CG ∴=120,120DCF FCG ∠=︒∠=︒,DCF ECG CFD CGE ∴∠=∠∴∆≅∆DF EG ∴=,OF OD DF OD EG OG OE EG ∴=+=+=-OF OG OD EG OE EG OD OE ∴+=++-=+OD OE ∴+=(3)结论为:OE OD -=.理由:过点C 作CF ⊥OA 于F ,CG ⊥OB 于G ,∴∠OFC =∠OGC =90°,∵∠AOB =60°,∴∠FCG =120°,同(1)的方法得,OF ,OG ,∴OF +OG ,∵CF ⊥OA ,CG ⊥OB ,且点C 是∠AOB 的平分线OM 上一点,∴CF =CG ,∵∠DCE =120°,∠FCG =120°,∴∠DCF =∠ECG ,∴△CFD ≌△CGE ,∴DF =EG ,∴OF =DF−OD =EG−OD ,OG =OE−EG ,∴OF +OG =EG−OD +OE−EG =OE−OD ,∴OE−OD OC .【点睛】此题属于几何变换综合题,主要考查了角平分线的性质,全等三角形的判定和性质的综合运用,正确作出辅助线,构造全等三角形是解本题的关键. 7. 如图,一伞状图形,已知120AOB ∠=︒,点P 是AOB ∠角平分线上一点,且2OP =,60MPN ∠=︒,PM 与OB 交于点F ,PN 与OA 交于点E .(1)如图一,当PN 与PO 重合时,探索PE ,PF 的数量关系(2)如图二,将MPN ∠在(1)的情形下绕点P 逆时针旋转α度()060α<<︒,继续探索PE ,PF 的数量关系,并求四边形OEPF 的面积.【答案】(1)=PE PF ,证明详见解析;(2)=PE PF 【解析】【分析】(1)根据角平分线定义得到∠POF=60°,推出△PEF 是等边三角形,得到PE=PF ;(2)过点P 作PQ ⊥OA ,PH ⊥OB ,根据角平分线的性质得到PQ=PH ,∠PQO=∠PHO=90°,根据全等三角形的性质得到PE=PF ,S 四边形OEPF =S 四边形OQPH ,求得OQ=1,,根据三角形的面积公式即可得到结论.【详解】解:(1)∵120AOB ∠︒=,OP 平分AOB ∠, ∴60POF ∠︒=,∵60MPN ∠︒=,∴60MPN FOP ∠∠︒== ,∴PEF ∆是等边三角形,∴=PE PF ;(2)过点P 作PQ OA ⊥,PH OB ⊥,∵OP 平分AOB ∠,∴PQ PH =,90PQO PHO ∠∠︒==,∵120AOB ∠︒=, ∴∠QPH =60°,∴QPE FPH EPH ∠+∠+∠,∴QPE EPF ∠∠=,在QPE ∆与HPF ∆中EQP FHP QPE HPF PQ PH ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴QPE HPF AAS ∆∆≌(),∴=PE PF ,OEPF OQPH S S 四边形四边形=,∵PQ OA ⊥,PH OB ⊥,OP 平分AOB ∠,∴30QPO ∠︒=,∴1OQ =,QP=∴112OPQ S ∆⨯⨯=∴四边形OEPF 的面积=2OPQ S ∆【点睛】本题考查了旋转的性质,角平分线的性质,全等三角形的判定和性质,三角形的面积,正确的作出辅助线是解题的关键.8. (1)方法导引:问题:如图1,等边三角形ABC 的边长为6,点O 是ABC ∠和ACB ∠的角平分线交点,120FOG ︒∠=,绕点O 任意旋转FOG ∠,分别交ABC 的两边于D ,E 两点.求四边形ODBE 面积.讨论:①小明:在FOG ∠旋转过程中,当OF 经过点B 时,OG 一定经过点C .②小颖:小明的分析有道理,这样我们就可以利用“ASA ”证出ODB OEC ≌. ③小飞:因为ODB OEC ≌,所以只要算出OBC 的面积就得出了四边形ODBE 的面积.老师:同学们的思路很清晰,也很正确.在分析和解决问题时,我们经常会借用特例作辅助线来解决一般问题:请你按照讨论的思路,直接写出四边形ODBE 的面积:________.(2)应用方法:①特例:如图2,FOG ∠的顶点O 在等边三角形ABC 的边BC 上,2OB =,4OC =,边OG AC ⊥于点E ,OF AB ⊥于点D ,求BOD 的面积.②探究:如图3,已知60FOG ︒∠=,顶点O 在等边三角形ABC 的边BC 上,2OB =,4OC =,记BOD 的面积为x ,COE 的面积为y ,求xy 的值. ③应用:如图4,已知60FOG ︒∠=,顶点O 在等边三角形ABC 的边CB 的延长线上,2OB =,6BC =,记BOD 的面积为a ,COE 的面积为b ,请直接写出a 与b 的关系式.【答案】(1)(2)①BOD 的面积=xy=12;③48ab =. 【解析】 【分析】(1)连接OB 、OC ,利用ASA 证出ODB OEC ≌,从而得出OBC 的面积与四边形ODBE 的面积相等,过点O 作OH BC ⊥于H 点,利用锐角三角函数求出OH 即可求出△OBC 的面积,从而得出结论;(2)①根据等边三角形的性质可得60B ︒∠=,从而求出∠BOD ,然后根据30°所对的直角边是斜边的一半和勾股定理即可求出OD 和BD ,从而求出结论; ②过点O 作OM AB ⊥于M ,ON AC ⊥于N ,根据相似三角形判定定理可得BDO COE ∽,根据相似三角形的性质列出比例式,变形可得8BD EC OB OC ⋅=⋅=,然后根据三角形的面积公式即可求出结论;③过点O 作OM AB ⊥交AB 的延长线于M ,ON AC ⊥于N ,根据相似三角形的判定定理可得BDO COE ∽,根据相似三角形的性质列出比例式,变形可得16BD EC OB OC ⋅=⋅=,分别求出OM 和ON ,再结合三角形的面积公式即可求出结论.【详解】解:(1)连接OB 、OC∵ABC 是等边三角形,∴60ABC ACB ︒∠=∠=∵O 是ABC ∠和ACB ∠的角平分线交点∴30DBO OCG CBO ︒∠=∠=∠=∴OB OC =,120BOC FOG ︒∠=∠=∴DOB COE ∠=∠∴ODB OEC ≌∴OBC 的面积与四边形ODBE 的面积相等过点O 作OH BC ⊥于H 点∵6BC =,∴3BH =∵30CBO ︒∠=,∴tan =•∠=OH BH OBH∴162OBC S =⨯⨯=∴四边形ODBE 的面积为故答案为:(2)①∵ABC 是等边三角形,∴60B ︒∠=∵OF AB ⊥于点D ,∴30BOD ︒∠=∵2OB =,∴112BD OB ==,OD ,∴BOD 的面积1122=⨯⨯= ②过点O 作OM AB ⊥于M ,ON AC ⊥于N .由①得:OM =ON =∵ABC 是等边三角形,∴60B C ︒∠=∠=∵60FOG ︒∠=,∴120BDO DOB EOC DOB ︒∠+∠=∠+∠=∴BDO EOC =∠∠,∴BDO COE ∽ ∴OB BD EC OC=, ∴8BD EC OB OC ⋅=⋅=∴1122⎫⎛⎫=⋅⋅=⎪ ⎪⎭⎝⎭xy ③48ab =过点O 作OM AB ⊥交AB 的延长线于M ,ON AC ⊥于N .∵60BDO DOC ABC ︒∠+∠=∠=,∴60FOG EOC DOC ︒∠=∠+∠=∴BDO EOC =∠∠,∵120DBO ECO ︒∠=∠=∴BDO COE ∽, ∴OB BD EC OC= ∴16BD EC OB OC ⋅=⋅=∵60OBN ABC ︒∠=∠=,2OB =,∴30BOM ∠=︒,∴OM =∵60ACB ∠=︒,8OC =,∴30CON ∠=︒,∴ON =∴1482⎫⎛⎫=⋅⋅=⎪ ⎪⎭⎝⎭ab 【点睛】此题考查的是全等三角形的判定及性质、等边三角形的性质、相似三角形的判定及性质和锐角三角函数,掌握全等三角形的判定及性质、等边三角形的性质、相似三角形的判定及性质和锐角三角函数是解决此题的关键.类型七-全等型α条件:①∠AOB = 2α, ∠DCE = 180- 2α.; ②CD=CE ;结论:①OC 平分∠AOB ;②OD+ OE = 2OC .cosα③S四边形ooc E = S△oc D +S△oc E = OC2sinαcosα当∠DCE的一边交AO的延长线于点D时,上述条件不变,结论有所变化9. 综合实践初步探究:如图,已知∠AOB=60°,在∠AOB的平分线OM上有一点C,将一个120°角的顶点与点C重合,它的两条边分别与直线OA、OB相交于点D、E.(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系为;解决问题:(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?若成立,请给于证明;若不成立,线段OD、OE与OC之间的数量关系为;拓展应用:(4)当∠DCE绕点C旋转到CD与OA垂直时,请猜想四边形CDOE的周长与OC 的数量关系,并说明理由;【答案】(1)OC;(2)仍然成立,理由见解析;(3)不成立,OE-OD=OC ;(4)四边形CDOE 的周长为,理由见解析. 【解析】【分析】(1)先判断出∠OCE=60°,再利用特殊角的三角函数得出,同理OE=2OC ,即可得出结论;(2)同(1)的方法得OC ,再判断出△CFD ≌△CGE ,得出DF=EG ,最后等量代换即可得出结论;(3)同(2)的方法即可得出结论;(4)同(1)可得,CD+CE=OC ,进而可得结论.【详解】:(1)∵OM 是∠AOB 的角平分线,∴∠AOC=∠BOC=12∠AOB=30°, ∵CD ⊥OA ,∴∠ODC=90°,∴∠OCD=60°,∴∠OCE=∠DCE-∠OCD=60°,在Rt △OCD 中,OD=OC •cos30°,同理:OE=2OC ,∴;(2)(1)中结论仍然成立,理由:过点C 作CF ⊥OA 于F ,CG ⊥OB 于G ,∴∠OFC=∠OGC=90°,∵∠AOB=60°,∴∠FCG=120°,同(1)的方法得,OF=2OC ,OG=2OC ,∴,∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,∴CF=CG,∵∠DCE=120°,∠FCG=120°,∴∠DCF=∠ECG,∴△CFD≌△CGE,∴DF=EG,∴OF=OD+DF=OD+EG,OG=OE-EG,∴OF+OG=OD+EG+OE-EG=OD+OE,∴;(3)(1)中结论不成立,结论为:,理由:过点C作CF⊥OA于F,CG⊥OB于G,∴∠OFC=∠OGC=90°,∵∠AOB=60°,∴∠FCG=120°,同(1)的方法得,,,∴,∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,∴CF=CG,∵∠DCE=120°,∠FCG=120°,∴∠DCF=∠ECG,∴△CFD≌△CGE,∴DF=EG,∴OF=DF-OD=EG-OD,OG=OE-EG,∴OF+OG=EG-OD+OE-EG=OE-OD,∴.(4)由(1)可得,CD+CE=OC∴,故四边形CDOE的周长为.【点睛】此题是几何变换综合题,主要考查了角平分线的定义和定理,全等三角形的判定和性质,特殊角的三角函数直角三角形的性质,正确作出辅助线是解本题的关键.第31页共31页。
专题05 对角互补模型(解析版)

专题05 对角互补模型基本模型:例题精讲例1.在△ABC 中,AB =AC ,∠BAC =90°,点D 是BC 的中点,FD ⊥ED .(1)如图1,若点E 在线段AB 上,点F 在线段AC 上,求证 BE =AF ;(2)如图 2,若点E 在线段AB 的延长线上,点F 在线段CA 的延长线上.请问(1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由.【答案】(1)见解析;(2)成立,见解析【解析】(1)证明:连接AD .如图1所示,∵AB AC =,90BAC ∠=︒,点D 是BC 的中点,∴45B C ∠=∠=︒,AD BC ⊥,1452DAF BAD BAC ∠=∠=∠=︒, ∴B DAF ∠=∠,90ADB ∠=︒,∴ABD △为等腰直角三角形,AD BD =,又∵FD ED ⊥,∴90EDF ∠=︒,∴BDE ADF ∠=∠,在BDE 和ADF 中,B DAF BD AD BDE ADF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()BDE ADF ASA ≌.∴BE AF =;(2)解:BE AF =仍然成立.证明:连接AD ,如图2所示.同①得:BDE ADF ∠=∠,AD BD =,45ABD CAD ∠=∠=︒,∴135DBE DAF ∠=∠=︒,在BDE 和ADF 中,BDE ADF BD AD DBE DAF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()BDE ADF ASA ≌,∴BE AF =.例2.已知:如图,在等边△ABC 中,点O 是BC 的中点,∠DOE =120°,∠DOE 绕着点O 旋转,角的两边与AB 相交于点D ,与AC 相交于点E .(1)若OD ,OE 都在BC 的上方,如图1,求证:OD =OE .(2)在图1中,BD ,CE 与BC 的数量关系是 .(3)若点D 在AB 的延长线上,点E 在线段AC 上,如图2,直接写出BD ,CE 与BC 的数量关系是 . 【答案】(1)见解析;(2)()2CE BD BC +=;(3)2()CE BD BC -=【解析】(1)证明:取AB 的中点F ,连接OF .∵△ABC 是等边三角形,∴,60AB BC ABC ACB =∠=∠=︒,∵点O 与点F 分别是BC 与AB 的中点,∴BF BO OC ==,∴△BOF 是等边三角形,∴OF OB OC ==,60OFD OCE BOF ∠=∠=∠=︒,∴120COF DOE ∠=︒=∠,∴DOF EOC ∠=∠,∵在△DOF 和△EOC 中,OFD OCE OF OC DOF EOC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴()DOF EOC ASA ≅,∴OD OE =.(2)解:结论:()2CE BD BC +=.理由:∵DOF EOC ≌,∴DF EC =,∴BD EC BD DF BF +=+=, ∵BOF 是等边三角形,∴OB BF =,∵2BC OB =,∴()2CE BD BC +=.故答案为:()2CE BD BC +=;(3)结论:2()CE BD BC -=.理由如图2中,取AB 的中点F ,连接OF .同(1)中的方法可证BOF 是等边三角形,DOF EOC ≌,∴DF CE =,∴EC BD DF BD BF OB -=-==,∵2BC OB =,∴2()CE BD BC -=例3.在七年级下册“证明”的一章的学习中,我们曾做过如下的实验:画∠AOB=90°,并画∠AOB的平分线OC.把三角尺的直角顶点落在OC的任意一点P上,使三角尺的两条直角边分别与OA、OB相交于点E、F.(1)若PE⊥OA,PF⊥OB(如图①),PE与PF相等吗?请说明理由;(2)把三角尺绕点P旋转(如图②),PE与PF相等吗?请说明理由;(3)探究:画∠AOB=50°,并画∠AOB的平分线OC,在OC上任取一点P,作∠EPF=130°.∠EPF的两边分别与OA、OB相交于E、F两点(如图③),PE与PF相等吗?请说明理由.【答案】(1)相等,见解析;(2)PE=PF,见解析;(3)PE=PF,见解析【解析】(1)解:∵OC平分∠AOB,PE⊥OA,PF⊥OB,∴PE=PF;(2)解:PE=PF,理由如下:当PE⊥OA时,如图①,∵∠AOB=90°,OC平分∠AOB,∴∠POE=∠POF=45°,∵∠PEO=∠EPF=∠EOF=90°,且∠PEO+∠EPF+∠EOF+∠PFO=360°,∴∠PFO=90°,∴∠PEO=∠PFO,∵OP=OP,∴△PEO≌△PFO(AAS),∴PE=PF;当PE与OA不垂直时,如图②,作PM⊥OA于点M,PN⊥OB于点N,∵∠OMP=∠ONP=90°,∠POM=∠PON=45°,OP=OP,∴△POM≌△PON(AAS),∴PM=PN,∵∠OMP=∠ONP=∠MON=90°,且∠OMP+∠ONP+∠MON+∠MPN=360°,∴∠MPN=90°,∵∠EPF=90°,∴∠MPE=∠NPF=90°﹣∠EPN,∵∠PME=∠PNF=90°,∴△PME≌△PNF(ASA),∴PE=PF,综上所述,PE=PF.(3)解:PE=PF,理由如下:如图③,在OF上取一点G,使OG=OE,连接PG,∵OC平分∠AOB,∴∠POG=∠POE,∵OP=OP,∴△POG≌△POE(SAS),∴∠OGP=∠OEP,PG=PE,∴∠PGF+∠OEP=∠PGF+∠OGP=180°,∴∠AOB=50°,∠EPF=130°,且∠AOB+∠EPF+∠PFG+∠OEP=360°,∴∠PFG+∠OEP=180°,∴∠PGF=∠PFG,∴PG=PF,∴PE=PF.课后训练1.如图,△ABC是边长为4的等边三角形,点D是线段BC的中点,∠EDF=120°,把∠EDF绕点D旋转,使∠EDF 的两边分别与线段AB 、AC 交于点E 、F .(1)当DF ⊥AC 时,求证:BE=CF ;(2)在旋转过程中,BE+CF 是否为定值?若是,求出这个定值;若不是,请说明理由【答案】(1)证明见解析;(2)是,2.【详解】(1)∵△ABC 是边长为4的等边三角形,点D 是线段BC 的中点,∴∠B=∠C=60°,BD=CD , ∵DF ⊥AC ,∴∠DFA=90°,∵∠A+∠EDF+∠AFD+∠AED=180°,∴∠AED=90°,∴∠DEB=∠DFC ,且∠B=∠C=60°,BD=DC ,∴△BDE ≌△CDF (AAS )(2)过点D 作DM ⊥AB 于M ,作DN ⊥AC 于N ,则有∠AMD=∠BMD=∠AND=∠CND=90°.∵∠A=60°,∴∠MDN=360°-60°-90°-90°=120°.∵∠EDF=120°,∴∠MDE=∠NDF .在△MBD 和△NCD 中,BMD CND B C BD CD ∠∠⎧⎪∠∠⎨⎪⎩===,∴△MBD ≌△NCD (AAS ),BM=CN ,DM=DN .在△EMD 和△FND 中,EMD FND DM DNMDE NDF ∠∠⎧⎪⎨⎪∠∠⎩===,∴△EMD ≌△FND (ASA )∴EM=FN , ∴BE+CF=BM+EM+CF=BM+FN+CF=BM+CN=2BM=2BD×cos60°=BD=12BC=2.2.如图,点P (3m -1,-2m +4)在第一象限的角平分线OC 上,AP ⊥BP ,点A 在x 轴正半轴上,点B 在y 轴正半轴上.(1)求点P 的坐标.(2)当∠APB 绕点P 旋转时,①OA +OB 的值是否发生变化?若变化,求出其变化范围;若不变,求出这个定值.②请求出OA 2+OB 2的最小值.【答案】(1)P (2,2);(2)①不变,定值为4;②OA 2+OB 2的最小值为8.【解析】(1)解:∵点P (3m -1,-2m +4)在第一象限的角平分线OC 上,∴3m -1=-2m +4,∴m =1,∴P (2,2);(2)①过点P 作PM ⊥y 轴于M ,PN ⊥OA 于N .∵∠PMO =∠PNO =∠MON =90°,∴四边形OMPN 是矩形,∵OP 平分∠MON ,PM ⊥OM ,PN ⊥ON ,∴PM =PN ,∴四边形OMPN 是正方形,∵P (2,2),∴PM =PN =OM =ON =2,∵AP ⊥BP ,∴∠APB =∠MPN =90°,∴∠MPB +∠BPN =∠BPN +∠NP A =90°,∴∠MPB =∠NP A ,在△PMB 和△PNA 中,MPB NPA PM PN PMB PNA ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△PMB ≌△PNA (ASA ),∴BM =AN ,∴OB +OA =OM -BM +ON +AN =2OM =4.②连接AB ,∵∠AOB =90°,∴OA 2+OB 2=AB 2.∵∠BP A =90°,∴AB 2=P A 2+PB 2=2P A 2,∴OA 2+OB 2=2P A 2,当P A 最小时,OA 2+OB 2也最小.根据垂线段最短原理,P A 最小值为2.∴OA 2+OB 2的最小值为8.3.一位同学拿了两块45︒三角尺MNK ∆,ACB ∆做了一个探究活动:将MNK ∆的直角顶点M 放在ACB ∆的斜边AB 的中点处,设4AC BC ==.(1)如图1所示,两三角尺的重叠部分为ACM ∆,则重叠部分的面积为______,周长为______.(2)将如图1所示中的MNK ∆绕顶点M 逆时针旋转45︒,得到如图2所示,此时重叠部分的面积为______,周长为______.(3)如果将MNK ∆绕M 旋转到不同于如图1所示和如图2所示的图形,如图3所示,请你猜想此时重叠部分的面积为______.【答案】(1)4,4+(2)4,8;(3)4;(4)4+【详解】解:()14AC BC ==,90ACB ∠=,AB ∴==M 是AB 的中点,AM ∴=45ACM ∠=,AM MC ∴=,∴4=, ∴周长为:44AM MC AC ++==+4,4+;()2重叠部分是正方形,∴边长为1422⨯=,面积为14444⨯⨯=, 周长为248⨯=.故答案为4,8.()3过点M 分别作AC 、BC 的垂线MH 、ME ,垂足为H 、E , M 是ABC 斜边AB 的中点,4AC BC ==,12MH BC ∴=,12ME AC =,MH ME ∴=, 又90NMK HME ∠∠==,90NMH HMK ∠∠∴+=,90EMG HMK ∠∠+=,HMD EMG ∠∠∴=,在MHD 和MEG 中,HMD GME MH ME DHM MEG ∠=∠⎧⎪=⎨⎪∠=∠⎩,MHD ∴≌()MEG ASA ,∴阴影部分的面积等于正方形CEMH 的面积,正方形CEMH 的面积是1144422ME MH ⋅=⨯⨯⨯=;∴阴影部分的面积是4;故答案为4. ()4如图所示, 过点M 作ME BC ⊥于点E ,MH AC ⊥于点H ,∴四边形MECH 是矩形, MH CE ∴=,45A ∠=, 45AMH ∠∴=, AH MH ∴=,AH CE ∴=,在Rt DHM 和Rt GEM 中,DMH EMG MH MEDHM GEM ∠=∠⎧⎪=⎨⎪∠=∠⎩,Rt DHM ∴≌.Rt GEM GE DH ∴=,AH DH CE GE ∴-=-, CG AD ∴=,1AD =, 1.DH ∴=DM ∴==.∴四边形DMGC 的周长为:CE CD DM ME +++ 2AD CD DM =++4=+.4.如图所示,ABC ∆为等边三角形,边长为4,点O 为BC 边中点,120EOF ∠=︒,其两边分别交AB 和CA 的延长线于E ,F ,求AE AF -的值.【答案】6【详解】过点O 作OD ∥AB 交AC 于点D ,∴∠CDO=∠A=∠ACB=∠ABC=60°,∴∠DOC=60°,∠ADO=∠BOD=120°.∴△CDO 是等边三角形,∴DO=CO ,∴DO=BO=AD .∵△ABC 是等边三角形,∴AB=AC=BC .∠CAB=∠ABC=∠C=60°,∴∠OBE=120°,∴∠ODF=∠OBE .∵∠FOB+∠BOE=∠EOF=120°,∠DOF+∠FOB=∠BOD=120°∴∠FOD=∠EOB .在△DOF 和△BOE 中,ODF OBE DO BO FOD EOB ∠∠⎧⎪⎨⎪∠∠⎩===,∴△DOF ≌△BOE (ASA ).∴FC=EB .OF=OE .∵AE=AB+BE ,∴AE=AB+DF ,∴AE=AB+AD+AF ,∴AE -AF=AB+AD .∵AB+AD=32AB ,∴AE -AF=32AB .∵AB=4,∴AE -AF=6.。
2023年九年级数学中考几何模型-对角互补模型 课件(共17张PPT)

∴∠BENE=∠FEM
∴△BEN∽△FEM
∴
EF BE
EM EN
∵EN‖AB EM‖AD
∴ EN CE EM AB AC AD
∴ EN EM AB AD
∵AB=3,BC=5=AD
∴
EM EN
5 3
EF BE
M N
不积跬步 无以至千里。
课堂检测
1、已知∠AOB=∠ACB=90°,OC平分∠AOB,OC=4,则四边形AOBC的面积是 ___8_____.
(
9 5
)2
3
不积跬步 无以至千里。
(相似型)例4、如图,在矩形ABCD中,AB=3,BC=5,点E在对角线AC上,
连接BE,作EF⊥BE,垂足为点E,交CD于点F,求
EF BE
的值.
证明:在矩形ABCD中,过点E作EN⊥BC,EM⊥DC
∴四边形ENCM是矩形
∴∠MEN=90°
∵EF⊥BE
∴∠BEF=90
D H F
EI
B
图1
不积跬步 无以至千里。
模型探究
如图2,在四边形中FBDE,∠EDF+∠EBF=180°,连接BD,∠DBE=∠CBF,若△BCD为等边三 角形,探究:线段DE、DF、BD之间的数量关系______B_D_=_D_F_+_D_E__;
证明:∵∠EDF+∠EBF=180° ∴∠DFB+∠DEB=180° ∴∠CFB=∠DEB ∵△BCD为等边三角形 ∴BC=BD ∵∠DBE=∠CBF ∴△FBC≌△EBD ∴DE=CF ∴BD=DC=DF+CF=DF+DE
∴AC=4
不积跬步 无以至千里。
(全等型)例2、如图,在平面直角坐标系xOy中,A,B两点分别在x轴,y轴的正半 轴上,且OA=OB,点C在第一象限,OC=3,连接BC,AC,若∠BCA=90°,则BC+AC的 值为___3__2____.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学几何-典型问题中的对角互补模型
一、等边三角形
1.已知:ABC ∆是等边三角形,12120∠+∠=︒,求证:1260∠=∠=︒.
2.已知:ABC ∆是等边三角形,160∠=︒,求证:260∠=︒.
3.已知:12BAC 60∠=∠=∠=︒,求证:ABC ∆是等边三角形.
4.已知:12360∠=∠=∠=︒,求证:ABC ∆是等边三角形.
5.已知:ABC ∆是等腰直角三角形,1290∠+∠=︒,求证:1245∠=∠=︒.
6.已知:ABC ∆是等腰直角三角形,145∠=︒,求证:245∠=︒.
7.已知:1245∠=∠=︒,BAC 90∠=︒,求证:ABC ∆是等腰直角三角形.
8.已知:12345∠=∠=∠=︒,求证:ABC ∆是等腰直角三角形.
9.已知:ABC ∆是等腰直角三角形,12135∠+∠=︒,求证:145∠=︒.
10.已知:ABC ∆是等腰直角三角形,145∠=︒,求证:290∠=︒.
11.已知:ABC ∆是等腰直角三角形,290∠=︒,求证:145∠=︒.
12.已知:145∠=︒,2BAC 90∠=∠=︒,求证:ABC ∆是等腰直角三角形.
13.已知:1345∠=∠=︒,290∠=︒,求证:ABC ∆是等腰直角三角形.。
