最新七年级下册数学思维专项训练题(共10套)
七年级下册数学思维拓展训练(每周一练)

卖出,该同学实际盈利为( )
A.400 元
B.382 元
C.340 元
D.370 元
二、填空题(每小题 4 分,共 24 分)
7.关于 x,y 的二元一次方程组
,求 =_____, =_______.
8. 如果 4x-5y=0,且 x≠0,那么
的值是_____,则 10 人无法安排;若每间住 3 人,则有 10 间无人住,这 批宿舍有_______间.
4
为 20 元的比票价为 10 元的多______张.
1
三、解答题 13.解方程组(每小题 5 分,共 20 分)
①
②
③
④
14. (6 分)已知方程组
与
有相同的解,求 m、n 的值。
2
15. (8 分)小明在拼图时,发现 8 个一样大小的⻓方形, 恰好可以拼成一个大的⻓方形如图(1);小红看⻅了, 说:“我也来试一试.”结果小红拼成了如图(2)那样 的正方形,中间还留下了一个洞,恰好是边⻓为 5mm 的小正方形,则每个小⻓方形的面积是多少?.
16.(8 分)某生产⻋间共有 36 名工人,已知每名工人每小时可以生产螺丝帽 50 个,或者生 产螺丝钉 20 个,已知一个螺丝钉要配两个螺丝帽,则如何安排人员才能使所生产的螺 丝帽与螺丝钉正好配套.
3
17.(10 分)数轴上点 A 对应的数为 a,点 B 对应的数为 b,点 A 在负半轴,且|a|=3, b 是最小的正整数. (Ⅰ )直接写出线段 AB 的⻓; (Ⅱ )若点 C 在数轴上对应的数为 x,且 x 是方程 2x+1=3x﹣4 的根,在数轴上是否存 在点 P 使 PA+PB= BC+AB,若存在,求出点 P 对应的数,若不存在,说明理由. (Ⅲ)如图,若 Q 是 B 点右侧一点,QA 的中点为 M,N 为 QB 的四等分点且靠近于 Q 点,当 Q 在 B 的右侧运动时,有两个结论:① QM+ BN 的值不变,②QM﹣ BN 的值不变,其中只有一个结论正确,请你判断正确的结论,并求出其值.
最近重庆忠县中学数学七年级思维训练试卷(含答案)

最近重庆忠县中学数学七年级思维训练试卷(含答案)第Ⅰ卷 选择题(共30分)一、选择题(本大题共10个小题,每小题3分,共30分.在每个小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑)1、下列结论中正确的是 ( ) A .0既是正数,又是负数 B .O 是最小的正数C .0是最大的负数D .0既不是正数,也不是负数2.在数轴上距离原点2个单位长度的点所表示的数是 ( ) (A) 2 (B)2- (C)2或2- (D)1或1-3.将下列各选项中的平面图形绕轴旋转一周,可得到如图所示的立体图形的是( )A. B. C. D.4.地球的表面积约为510 000 000 km 2,用科学计数法表示为( )km 2A .51×108B .5.1×108C .51×107D .5.1×1075.下列各组中的两项,属于同类项的是……………………………………………( )A .-2x 3与-2x 2B .12a 3b 与43ab 2 C .-125与15 D .0.5x 2y 与0.5x 2z6.把弯曲的道路改直,能够缩短行程,其道理用数学知识解释应是 ……………( )A.垂线段最短B.两点确定一条直线C.线段可以大小比较D.两点之间,线段最短7.超市出售的某种品牌的面粉袋上,标有质量为(25±0.2)kg的字样,从中任意拿出两袋,它们的质量最多相差…………………………………………………………()A. 0.2 kgB. 0.4 kgC. 25.2 kgD. 50.4 kg8.一根绳子弯曲成如图1的形状,用剪刀像图2那样沿虚线a把绳子剪断时,绳子被剪为5段;当用剪刀像图3那样沿虚线b(b∥a)把绳子再剪一次时,绳子就被剪为9段.若用剪刀在虚线a,b之间把绳子再剪(n-2)次(剪开的方向与a平行),这样一共剪n次时绳子的段数是( )A.4n+1 B.4n+2 C.4n+3 D.4n+59、一个数的绝对值是1/9,则这个数可以是()A.1/3B.1/9C.1/9或者-1/9D.-1/910.若x的相反数是3,|y|=5,则x+y的值为()A.-8 B.2 C.8或-2 D.-8或2第Ⅱ卷非选择题(共90分)二、填空题(本大题共5个小题,每小题3分,共15分)11、如果节约16度电记作+16度,那么浪费5度电记作度;12. 如图,∠AOB=90°,以O为顶点的锐角共有个13.已知a^2-b=8,b=8,则a-b的值为____________________.14. 给x取一个合适的有理数使|x+5|+|x+7|的值最小,这个最小值是15、观察下列图形及图形所对应的算式,根据你发现的规律计算1+8+16+24+ (136)三、解答题 (本大题共8个小题,共75分.解答应写出文字说明、证明过程或演算步骤)16. (1) (-28)÷(―6+4)+(―1)×5 (2) -14-[2―(―3)2]+(-1)4(3)、 33+(-32)+7-(-3) (4)、-|-32|÷3×(-)-(-2)317.解方程(每小题4分,共8分)(1) 3(x -4)=12; (2) x -x -12 =2-x +23.18.已知代数式:A=2x 2+3xy +2y -1,B=x 2-xy +x -12; (1)当x -y =-1,xy =1时,求A -2B 的值; (2)若A -2B 的值与x 的取值无关,求y 的值.19.阅读下面的文字,解答问题: 大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用−1来表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵<<,即2<<3,∴的整数部分为2,小数部分为(−2).请解答:(1)的整数部分是__________,小数部分是__________(2)如果的小数部分为a,的整数部分为b,求a+b−的值;20.如图,纸上有五个边长为1的小正方形组成的图形纸(图1),我们可以把它剪开拼成一个正方形(图2).(1)图2中拼成的正方形的的面积是▲;边长是▲;(填实数)(2)请你在图3中画一个面积为5的正方形,要求所画正方形的顶点都在格点上........请用虚线画出.(3)你能把十个小正方形组成的图形纸(图4),剪开并拼成正方形吗?若能,请仿照图2的形式把它重新拼成一个正方形.并求出它的边长.21.某通讯公司推出了移动电话的两种计费方式(详情见下表).月使用费/元主叫限定时间/分主叫超时费/(元/分)被叫方式一58 150 0.25 免费方式二88 350 0.19 免费设一个月内使用移动电话主叫的时间为t分(t为正整数),请根据表中提供的信息回答下列问题:(Ⅰ)用含有t的式子填写下表:(Ⅱ)当t为何值时,两种计费方式的费用相等?(Ⅲ)当330<t<360时,你认为选用哪种计费方式省钱(直接写出结果即可).22.A、B两地相距1755公里,甲、乙两辆汽车分别从A、B两地同时出发,相向而行.已知甲车比乙车平均每小时多行驶9公里,经过5小时,两车共行驶了675公里.〔1)求甲、乙两车平均每小时分别行驶多少公里?(2)若5小时后,甲车每小时比原来多行驶3.5公里,乙车每小时比原来多行5.5公里,按此速度行驶比按原速度行驶,两车可提前几小时相遇?23.(11分)已知O为直线AB上的一点,∠COE是直角,OF平分∠AOE.(1)如图1,若∠COF=34°,则∠BOE=;若∠COF=n°,则∠BOE=;∠BOE与∠COF 的数量关系为.(2)当射线OE绕点O逆时针旋转到如图2的位置时,(1)中∠BOE与∠COF的数量关系是否仍然成立?如成立请写出关系式;如不成立请说明理由.(3)在图3中,若∠COF=65°,在∠BOE的内部是否存在一条射线OD,使得2∠BOD与∠AOF的和等于∠BOE与∠BOD的差的一半?若存在,请求出∠BOD的度数;若不存在,请说明理由.。
七年级新思维数学试卷答案

1. 下列各数中,不是有理数的是()A. -2.5B. √2C. 0.1010010001…D. -1/3答案:B解析:有理数是可以表示为两个整数之比的数,包括整数、分数和小数。
选项B的√2是无理数,不能表示为两个整数之比。
2. 若a、b是实数,且a+b=0,则下列各式中,正确的是()A. a=0B. b=0C. a=-bD. ab=0答案:C解析:由题意知,a+b=0,则a=-b。
3. 下列各式中,正确的是()A. 3^2 = 9B. (-2)^3 = -8C. 2^0 = 1D. (-3)^2 = 9答案:B解析:A选项中的3^2=9是正确的,B选项中的(-2)^3=-8也是正确的,C选项中的2^0=1是正确的,D选项中的(-3)^2=9也是正确的。
但题目要求选择正确的式子,故选B。
4. 若a、b、c是三角形的三边长,则下列各式中,正确的是()A. a+b>cB. a-b>cC. a+b>cD. a-b>c答案:C解析:根据三角形的性质,任意两边之和大于第三边,故选C。
5. 下列各式中,正确的是()A. √9=±3B. √16=4C. √25=5D. √36=6答案:C解析:A选项中的√9=±3是错误的,因为√9=3;B选项中的√16=4是正确的;C 选项中的√25=5是正确的;D选项中的√36=6是正确的。
故选C。
1. 若x^2=9,则x=_________。
答案:±3解析:由平方根的定义可知,若x^2=9,则x=±3。
2. 若a=2,b=-3,则a^2+b^2=_________。
答案:13解析:将a、b的值代入公式,得a^2+b^2=2^2+(-3)^2=4+9=13。
3. 若x=5,则(x+2)^2=_________。
答案:49解析:将x的值代入公式,得(x+2)^2=5+2)^2=49。
4. 若x=3,则|x-2|=_________。
七年级下册数学思维专项训练题(共10套)

七年级下册数学思维专项训练题(共10套)思维训练题(一)班级______________ 姓名_____________ 一、选择题:1.a 为任意自然数,包括a 在内的三个连续的自然数,可以表示为 ( )A .a -2,a -1,aB .a -3,a -2,a -1C .a ,a +1,a +2D .不同于A 、B 、C 的形式二、计算题:(动动脑筋,可能会有简便的解题方法!)1.____________________56875=⨯2.____________2006200420022000...12108642=+-+-+-+-+- 3.__________________8567785667855678=+++4.()()__________888...6428002...888488868888=++++-++++5.______________125.01712517125625.05.0171251753=⨯-⨯+⨯+ 6.______________12346123451234512345=÷7._________________31313131=-+-8._______________99163135115131=++++ 9._____________20042004...200432004220041=++++10._____________90197218561742163015201412136121=++++++++三、应用与创新:1.有一高楼,每上一层需要3分钟,每下一层需要1分30秒。
小贤于下午6时15分开始从最底层不断地向上走,到了最顶层后便立即往下走,中途没有停留,他在7时36分返回最底层。
这座高楼共有多少层?2.回答下列各题:(1)用1、2、3、4、5、6、7、8可组成多少个没有重复数字的五位数?(2)在15个连续自然数中最多有多少个质数?最少有多少个质数?(3)以下是一个数列,第一项是1,第二项是4,以后每一项是前两项相乘的积。
七年级下数学思维训练试卷

一、选择题(每题3分,共30分)1. 下列各数中,有理数是()A. √16B. √-16C. √-1D. √02. 若a、b是方程x^2-5x+6=0的两个根,则a+b的值是()A. 5B. 6C. 4D. 73. 在直角坐标系中,点A(2,3)关于x轴的对称点坐标是()A. (2,-3)B. (-2,3)C. (2,-3)D. (-2,-3)4. 下列各式中,正确的是()A. |x|=-xB. |x|=xC. |x|≥0D. |x|≤05. 下列函数中,是反比例函数的是()A. y=2x+3B. y=x^2C. y=2/xD. y=√x6. 若m、n是方程x^2-3x+2=0的两个根,则m^2+n^2的值是()A. 4B. 6C. 7D. 87. 在△ABC中,∠A=60°,∠B=45°,则∠C的度数是()A. 75°B. 90°C. 105°D. 120°8. 若a、b、c、d为等差数列,且a+c=b+d,则下列选项中一定成立的是()A. a=dB. b=cC. a+c=2bD. a+d=2c9. 下列各数中,无理数是()A. √4B. √9C. √-4D. √-910. 若函数y=kx+b的图象经过点(1,2),则k+b的值是()A. 3B. 1C. 0D. -1二、填空题(每题5分,共20分)11. 若方程x^2-4x+3=0的两个根是m和n,则m+n的值是______。
12. 在△ABC中,∠A=45°,∠B=90°,则∠C的度数是______。
13. 若函数y=2x-3的图象经过点(0,y),则y的值是______。
14. 在等差数列{an}中,若a1=2,公差d=3,则第10项an的值是______。
15. 若等比数列{bn}中,b1=4,公比q=2,则第5项bn的值是______。
三、解答题(每题10分,共30分)16. 解方程:2x^2-5x+3=0。
七年级数学思维训练(共10套)5(2)

七年级数学思维训练(共10套)(第一套)班级______________ 姓名_____________一、选择题:1.a 为任意自然数,包括a 在内的三个连续的自然数,可以表示为 ( )A .a -2,a -1,aB .a -3,a -2,a -1C .a ,a +1,a +2D .不同于A 、B 、C 的形式二、计算题:(动动脑筋,可能会有简便的解题方法!)1.____________________56875=⨯2.____________2006200420022000...12108642=+-+-+-+-+-3.__________________8567785667855678=+++4.()()__________888...6428002...888488868888=++++-++++5.______________125.01712517125625.05.0171251753=⨯-⨯+⨯+ 6.______________12346123451234512345=÷ 7._________________31313131=-+-8._______________99163135115131=++++9._____________20042004...200432004220041=++++10._____________90197218561742163015201412136121=++++++++ 三、应用与创新:1.有一高楼,每上一层需要3分钟,每下一层需要1分30秒。
小贤于下午6时15分开始从最底层不断地向上走,到了最顶层后便立即往下走,中途没有停留,他在7时36分返回最底层。
这座高楼共有多少层?2.回答下列各题:(1)用1、2、3、4、5、6、7、8可组成多少个没有重复数字的五位数?(2)在15个连续自然数中最多有多少个质数?最少有多少个质数?(3)以下是一个数列,第一项是1,第二项是4,以后每一项是前两项相乘的积。
七年级奥数思维训练50题

七年级奥数思维训练50题1. 一个数p 为质数,并且p+10,p+14也是质数,p 是多少?除此之外还有别的数吗?2. 证明:大于12的整数都可以表示成两个合数之和。
3. 请同时取出六个连续的正整数,使它们满足:6个数中任取2个、3个、4个、5个、6个数之和都是合数,并简述理由。
4. 已知x 、y 、z 为整数,且11|(7x +2y −5z)。
求证:11|(3x −7y +12z)。
5. 已知定理:“若三个大于3的质数a 、b 、c 满足关系式2a+5b=c ,则a+b+c 是整数n 的倍数”。
问上述定理中的整数n 的最大可能值是多少?说明你的理由。
6. 已知六位数N 的前三位组成的数与后三位组成的数之和能被111整除。
求证:111|N 。
7. 若a 、b 、c 为整数,且|a −b |19+|c −a |99=1试求|c −a|+|a −b|+|b −cl 的值。
8. 海边有一堆苹果,第一只猴子拿走15,扔掉一个;第二只猴子又拿走剩下的15,扔掉一个;第三只猴子又拿走剩下的15,再扔掉一个。
试用代数式表示所说的意思及剩下的苹果数。
9. 父亲和儿子在100米的跑道上进行赛跑,已知儿子跑5步的时间父亲能跑6步,儿子跑7步的距离与父亲跑4步的距离相等.现在儿子站在100米的中点处,父亲站在100米跑道的起点处同时起跑.问父亲能否在100米的终点处超过儿子?并说明理由。
10. 一个负有理数a 在数轴上的位置为A ,那么在数轴上与A 相距d个单位(d>0)的点中,与原点距离最远的点所对应的数是多少?11.某城镇沿环形路上依次排列有五所小学:A1、A2、A3、A4、A5,它们顺次有电脑15台、7台、11台、3台、14台,为使各校的电脑数相同,允许一些小学向相邻小学调出电脑,问怎样调配才能使调出的电脑总台数最少?并求出电脑的最少总台数。
12.张三、李四和王五三人各有若干两金子,要求互相赠送。
先由张三给李四和王五,所给的金子数等于李四、王五原来各有的,依相同的方式再由李四给张三和王五现有金子数,后由王五给张三和李四现有金子数,互送后每人恰好有64两,问原来三人各有金子多少两?13.培育学校初一7班计划用班会费的66元钱,同时购买平价分别为3元、2元、1元的甲、乙、丙三种笔记本,奖励成绩好的同学,已知购买乙种笔记本的本数比购买甲种笔记本的本数多2本,而购买甲种笔记本的本数不少于10本,且购甲种笔记本的费用不超过总费用的一半,若购买的甲、乙、丙三种笔记本恰好用了66元,问可有几种购买方案,每种方案中购买的甲、乙、丙三种笔记本各多少本?14.有五位小朋友,他们是小明,小红,小华,小青,小琪,他们分别有苹果15个,7个,11个,3个,14个,现要使每位小朋友的苹果数相等,各调几个给邻友:小明给小红,小红给小华,小华给小青,小青给小琪,小琪给小明,若甲给乙一2个,即为乙给甲2个,要使移动的总数最小,应作怎样安排?15.某人从家到商店买东西,三分之一的路程骑自行车,三分之二的路程步行;返回时,三分之一的时间骑自行车,三分之二的时间步行,已知骑车速度为12千米/小时,步行速度为3千米/小时,且去时比返回时所用时间多3小时,那么家到商店的距离是多少千米?16.某人沿着向上移动的自动扶梯从顶朝下走到底用了7分30秒,而他沿着自动扶梯从底朝上走到顶只用了1分钟30秒,那么此人不走,乘着扶梯从底到顶需要用几分钟?又若停电,此人沿扶梯从底走到顶需几分钟(假定此人上、下扶梯的行走速度相同)。
2023 年第四届超常(数学)思维与创新能力测评 初一年级 数学真题
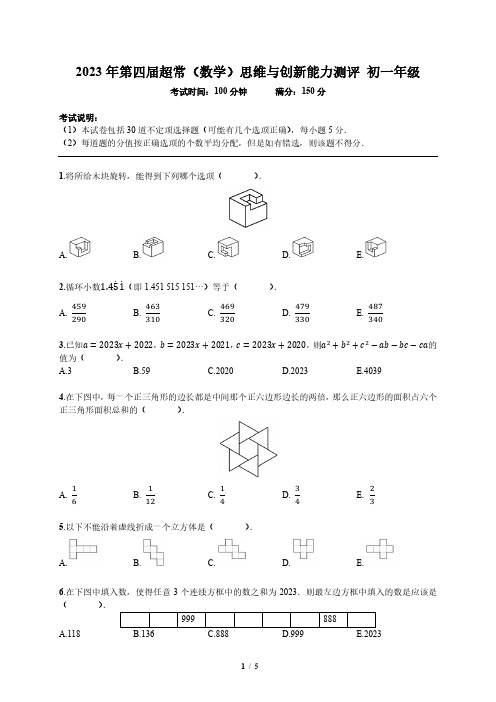
2023年第四届超常(数学)思维与创新能力测评 初一年级考试时间:100分钟满分:150分考试说明:(1)本试卷包括30道不定项选择题(可能有几个选项正确),每小题5分.(2)每道题的分值按正确选项的个数平均分配,但是如有错选,则该题不得分.1.将所给木块旋转,能得到下列哪个选项().A. B. C. D. E.2.循环小数1.451(即1.451 515 151…)等于(). A. 459290B.463310C.469320D. 479330E.4873403.已知a =2023x +2022,b =2023x +2021,c =2023x +2020,则a 2+b 2+c 2−ab −bc −ca 的值为( ).A.3 B.59 C.2020 D.2023 E.40394.在下图中,每一个正三角形的边长都是中间那个正六边形边长的两倍,那么正六边形的面积占六个正三角形面积总和的( ).A.16B.112C.14D.34E.235.以下不能沿着虚线折成一个立方体是().A. B. C. D. E.6.在下图中填入数,使得任意3个连续方框中的数之和为2023.则最左边方框中填入的数是应该是( ).A.1187.已知202009=102000∙409∙2n,则n的值为().A.1991B.2000C.2009D.4018E.50008.如图,某城有一组十分奇怪的限速规定:在离城1km处有一个120km/h的标牌,在离城12km处有一个60km/h的标牌,在离城13km处有一个40km/h的标牌,在离城14km处有一个30km/h的标牌,在离城15km处有一个24km/h的标牌,在离城16km处有一个20km/h的标牌,如果你从120km/h的标牌处出发一直以限定时速行驶,那么需要()才能到达该城.A.30sB.1min13.5sC.1min42sD.2min27sE.3min9.如图所示,三个正方形以顶点相连接在一起,图中已给出若干角的度数,则x的值是().A.41B.42C.43D.44E.4610.一辆自行车的链条在具有48个齿的前链齿轮上运行,通常经过具有18个齿的后轮轴的链齿轮.当后链齿轮每旋转一整圈时,踏板转过的角度是().A.135°B.360°C.960°D.120°E.6712°11.如图,一个立方体的八个角都被切去,形成一些三角形面.将该图形的所有24个角都用对角线连起来,这些对角线中穿过图形内部的共有()条.A.84B.108C.120D.142E.24012.把一个三位数首位前和末位后添写上1,这样得到的五位数比原来的三位数增加14789.则原来三位数的三个数字之和是().A.10B.9C.8D.7E.613. Ⅰ号混合液由柠檬汁、油和醋以1:2:3的比例配成,Ⅱ号混合液由同样三种液体以3:4:5的比例配成,将两种混合液倒在一起后,新的混合液的比例不可能是().A.2:5:8B.4:5:6C.3:5:7D.5:6:7E.7:9:1114.如图所示的网球场中有()个长方形.A.19B.29C.23D.30E.3115.已知|x−1|+|x−2|=1,则x的值().A.只能为1B.只能为2C.可能为任何实数 D.为满足1≤x≤2的一切实数E.以上都不对16.下图是一张城市的道路平面图,除了一条短对角线外,道路全是东西向或南北向的.由于一条路的修补而不可能从点X通过.从P到Q的所有可能走的路线中,有些路线是最短的.则这样的最短路线有()条.A.4B.7C.9D.14E.1617.甲、乙一起工作,甲每工作1天休息2天,乙每工作1天休息3天.已知第一天他们都在工作,最后一天乙肯定在工作.甲、乙同时休息时间比同时工作时间多128天.则他们从第一天到最后一天经过了()天.A.180B.308C.309D.312E.50018.要使关于x的方程ax−1=x+a无解,则a=().A.-1B.0C.1D.2E.以上都不对19.小刚和月月搭乘某航空公司的飞机从A地飞往B地,但因为他们的行李超出了航空公司规定的重量,所以要求他们支付附加费.航空公司收费方法是对超出规定的重量每千克收取相同的费用.小刚付了60元,月月付了100元.他们一共有52kg的行李,如果小刚自己带着两人的全部行李走,他将必须付340元.每人最多可带(不需要付附加费的)行李()kg.A.20B.15C.12D.18E.3020.一个4×4的反幻方是指将数1~16填入4×4方格表内,使得每行、每列、每条对角线上的数之和,经排序后恰好形成十个连续的正整数.如图是一个尚未完成的反幻方,则星号“*”所在方格内应填入().A.1B.2C.15D.16E.以上都不对21.某学校新建5个教室,平均每班减少6人.如果再建5个教室,那么平均每班又减少4人.假设学生总数保持不变,这个学校可能有()名学生.A.560B.600C.650D.720E.80022.在一个2023边形(可以是凹多边形)的内角中,锐角至多有()个.A.2023B.672C.944D.1345E.134923.在一列数1,2,3,…,10000中,有()个数恰好包含两个相邻的数字9.例如:993,1992和9929就是这样的数,而9295或1999则不是.A.270B.271C.280D.123E.26124.从1970年起小红开始收集日历且以后每年都这样做,直到以后每一年至少可用一本已经收集到的日历来代用时为止.则必须收集日历的最后年份是()年.A.1983B.1984C.1997D.2023E.以上都不对25.100个正整数之和为101101,则它们的最大公约数的最大可能值是().A.101B.1100C.1001D.2002E.1001026.如图所示,你有一些白色的1×12×1瓦片.当用这些瓦片以紧贴邻边的方式来覆盖一个3×1的矩形时,共可以设计出4种颜色方案(WWW,BWW,WBW,WWB).那么如果用这些瓦片来覆盖一个10×1的矩形,将可以设计出()种颜色方案.A.47B.89C.155D.286E.30027.已知A,B,C,D,E,F,G,H,I是9个互不相同的非零数字,满足:A除以B余C,D除以E余F,G除以H余I,那么ABC+DEF+GHI的结果是().A.1368B.1458C.1188D.2547E.195328.令s为真分数,即s<t,且为最简分数.若t的值为2到9,s,t为正整数,则符合条件的不同的真t分数有().A.26B.27C.28D.30E.3629.有27个同样大小的小正方体,每个小正方体的六个面上写着一个相同的数,且恰为1~27,用这27个小正方体拼成如图所示的大正方体.请根据如图所示的数据以及下面所给出的条件推断,从六个方向都看不见的小正方体的面上所写的数是().①数9,13和16在同一条直线上.②数22在9和6之间.③17紧挨着5和13,但与9不相邻.④14紧挨着24和27.⑤数20在14的上面.A.22B.20C.17D.9E.530.一个棱长为6的正方体被切割成若干个棱长为整数的小正方体,若这些小正方体的表面积之和是切割前的大正方体的表面积的10倍,则切割成的小正方体中,棱长为1的小正方体的个数可能为3().A.15B.24C.42D.56E.60。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级下册数学思维题(共10套)
思维训练题(一)
班级______________ 姓名_____________
一、选择题:
1.a 为任意自然数,包括a 在内的三个连续的自然数,可以表示为 ( )
A .a -2,a -1,a
B .a -3,a -2,a -1
C .a ,a +1,a +2
D .不同于A 、B 、C 的形式
二、计算题:(动动脑筋,可能会有简便的解题方法!)
1.____________________56875=⨯
2.____________2006200420022000...12108642=+-+-+-+-+-
3.__________________8567785667855678=+++
4.()()__________888...6428002...888488868888=++++-++++
5.______________125.017
12517125625.05.0171251753
=⨯-⨯+⨯+ 6.______________12346
123451234512345=÷ 7._________________31313131=-+-
8._______________99
163135115131=++++
9.
_____________20042004...200432004220041=++++
10._____________90
19721856174216301520141213
6121=++++++++
三、应用与创新:
1.有一高楼,每上一层需要3分钟,每下一层需要1分30秒。
小贤于下午6时15分开始从最底层不断地向上走,到了最顶层后便立即往下走,中途没有停留,他在7时36分返回最底层。
这座高楼共有多少层?
2.回答下列各题:
(1)用1、2、3、4、5、6、7、8可组成多少个没有重复数字的五位数?
(2)在15个连续自然数中最多有多少个质数?最少有多少个质数?
(3)以下是一个数列,第一项是1,第二项是4,以后每一项是前两项相乘的积。
求第2004项被7除的余数。
项数 第1项 第2项 第3项 第4项 第5项 (2004)
数字 1 4 4 16 64 …… ?
思维训练题(二)
班级______________ 姓名_____________
一、填空题:
1.已知4个矿泉水的空瓶可换矿泉水一瓶,现有15个矿泉水空瓶,若不交钱,最多可换_____________瓶矿泉水喝。
2.有A 、B 、C 、三种不同的树苗若干,现要将它们植在如图所示的四个正方形空地中,要求:相邻的两棵不能相同,而对角的两棵可以相同,问共有多少种不同的植法?___________
3.乘火车从A 站出发,沿途出发经过3个车站方可到达B 站,那么在A 、B 两站之间共需要安排_________种不同的车票。
4.若分数m
1的分子加上a ,则它的分母上应加__________才能保证分数的值不变。
二、计算题:
1.()()()b a b a b a 88...22++++++
2.100
...6421...642142121+++++++++++
3.
56511...161111161611⨯++⨯+⨯+⨯
4.30
152412189126631510128966432⨯+⨯+⨯+⨯+⨯⨯+⨯+⨯+⨯+⨯
三、应用与创新:
1.某办事处由A 、B 、C 、D 、E 、F 六人轮流值夜班,规定轮班次序是A →B →C →D →E →F →A →B ……,在2005年的第一个星期里,元月1日恰是星期六,由A 值班,问2005年9月1日是谁值日?
2.1898年6月9日英国强迫清政府签约将香港975.1平方公里土地租借给英国99年,1997年7月1日香港回归祖国,中国人民终于洗刷了百年耻辱,已知1997年7月1日是星期二,那么1898年6月9日是星期几?
(注: 公历纪年,凡年份是4的倍数但不是100的倍数的那年为闰年,年约为400的倍数的那么也为闰年,闰年的二月有29天,平年的二月有28天。
)
3.一次考试有若干考生,顺序编号为1、2、3……,考试那天有一人缺考,剩下考生的编号和为2005,求考生人数以及缺考的学生的编号。
思维训练题(三)
班级_______________ 姓名_______________
一、填空题:
1.若b = a+5,b = c+10,则a、c的关系是________________。
2.如果一个自然数a与另一个自然数b的商恰好是其中一个数,那么b =
______________,或者满足条件____________________________。
3.若|a-1| = 1-a,那么a的取值条件是______________________。
4.若|a+b| = |a|+|b|,那么a、b应满足的条件是____________________。
5.a、b、c在数轴的位置如图所示,
则化简:|a|-|a+b|+|c-b|+|a+c|的结果
是________________。
a b 0 c 6.若|x-2|+|y+1| = 0,则x = ______________,y = ______________。
二、化简:
1.若x <-2,试化简:|x+2|+|x-1|
2.若x <-3,化简:|3+|2-|1+x|||
三、解方程:
1.|2x-1| = 3 2.|2x-5| = |x-1|。
