驻波是两列振幅
驻波
2 A cos 2
节点两侧质点反相
0
即:两节点间质点沿相反方向达到各自的最大值, 又同时沿相反方向通过平衡位置 结论:相邻两节点间的质点同相,节点两侧质点反相。
四、反射波的相位变化
实验1):反射点为固定端
C
C
解释:
C
F'
a a
F
b
质点b要带动a向上运 动b却受一反作用力 F '
C
x
cos 2π t
x1处质点B振动方程:
y x x1 ( 2 A cos 2
x2处质点C振动方程:
x1
) cos 2t ) cos 2t
y x x2 ( 2 A cos 2
各处质点振幅不同:
x2
0 A质 点 2 A
驻波方程 y 2 A cos 2π
1
2
l
1
4
2 2 l 2
33 l 2
32 l 4 53 l 4
讨论
如图二胡弦长 l 0.3 m ,张力 T 9.4N . 密度 3.8 104 kg m . 求弦所发的声音的基频和谐频. 解 :弦两端为固定点,是波节.
ln
千斤
nu 频率 2l
u n n 应满足 l n , 2 2l
两端固定的弦线形成驻波时,波长 n 和弦线长 l
n
n 1,2, 由此频率
决定的各种振动方式称为弦线振动的简正模式.
两端固定的弦 振动的简正模式
一端固定一端自由 的弦振动的简正模式
ln
n
2
n 1,2,
l
1 n l (n ) n 1,2, 2 2
驻波

波腹 x = ±k
λ
2
k = 0,1,2பைடு நூலகம்L 波节 x = ±( k + )
相邻波腹间的距离为: 相邻波腹间的距离为: ∆x = (k +1) 相邻波节间的距离为: ∆x = λ 2 相邻波节间的距离为: 相邻波腹与波节间的距离为: 相邻波腹与波节间的距离为: λ
λ
2
1 λ k = 0,1,2,L 2 2
2πx
λ
)
x
λ
cosωt
x
A( x) = 2Acos 2π
λ
y = A( x ) cosωt
函数不满足 y( t + ∆t , x + u∆t ) = y( t , x )
它不是行波
它表示各点都在作简谐振动, 它表示各点都在作简谐振动,各点振动的频 简谐振动 率相同,是原来波的频率。 率相同,是原来波的频率。但各点振幅随位置的 不同而不同。 不同而不同。 驻波的特点:不是振动的传播, 驻波的特点:不是振动的传播,而媒质中各质点 特点 都作稳定的振动。 都作稳定的振动。
当波从波密媒质垂直入射 当波从波密媒质垂直入射 到波疏媒质界面上反射时 到波疏媒质界面上反射时 无半波损失, ,无半波损失,界面处出 波腹。 现波腹。
无半波损失
2Acos 2π
x
λ
<0
驻波2.exe
节点两侧质点反相
总之:相邻两节点间的质点同相,节点两侧质 总之:相邻两节点间的质点同相, 点反相。 点反相。 纵驻波: 纵驻波:
应用程序
X 节点 节点
3、驻波的能量 Y X
驻波中的能流密度为零,实际上是系统的一 驻波中的能流密度为零, 种稳定的振动状态。 种稳定的振动状态。 驻波振动中无位相传播, 驻波振动中无位相传播,也无能量的传播 一个波段内不断地进行动能与势能的相互转换, 一个波段内不断地进行动能与势能的相互转换, 并不断地分别集中在波腹和波节附近而不向外 传播。 传播。
驻波实验报告实验原理

一、实验原理1. 驻波的形成驻波是两列振幅相等、频率相同、传播方向相反的波叠加形成的特殊波动现象。
当这两列波在空间相遇时,它们的振动方向相反,从而产生相互抵消的现象。
这种相互抵消的现象在空间上形成一系列稳定的波峰和波谷,称为驻波。
2. 驻波的特征(1)波节:驻波中振幅为零的点,称为波节。
波节在空间上固定不动,不会发生振动。
(2)波腹:驻波中振幅最大的点,称为波腹。
波腹在空间上固定不动,不会发生振动。
(3)波节间的距离:相邻波节之间的距离等于半个波长。
(4)波腹间的距离:相邻波腹之间的距离等于半个波长。
3. 驻波的形成条件(1)两列波振幅相等:只有当两列波的振幅相等时,它们在空间相遇才能形成稳定的驻波。
(2)两列波频率相同:只有当两列波的频率相同时,它们在空间相遇才能形成稳定的驻波。
(3)两列波传播方向相反:只有当两列波的传播方向相反时,它们在空间相遇才能形成稳定的驻波。
4. 驻波与波速的关系驻波的形成与波速有关。
当两列波在空间相遇时,它们的传播速度相同。
设波速为v,波长为λ,则频率f与波速v的关系为:v = fλ5. 驻波与弦线的关系在弦线上形成驻波时,弦线的长度应满足以下条件:(1)弦线长度为波长的整数倍:当弦线长度为波长的整数倍时,可以形成稳定的驻波。
(2)弦线两端固定:只有当弦线两端固定时,才能形成稳定的驻波。
6. 驻波实验原理驻波实验旨在验证驻波的形成条件、特征以及与波速、弦线的关系。
实验过程中,通过调节弦线长度、波源频率和张力,观察驻波的形成、变化和消失,从而验证驻波实验原理。
实验步骤如下:(1)搭建实验装置,包括弦线、波源、滑轮等。
(2)调节弦线长度,使其满足形成驻波的条件。
(3)调节波源频率,使其与弦线长度对应的波长匹配。
(4)观察驻波的形成、变化和消失,记录实验数据。
(5)分析实验数据,验证驻波实验原理。
通过驻波实验,我们可以了解驻波的形成条件、特征以及与波速、弦线的关系,为后续的物理学习和研究奠定基础。
驻波与克拉尼图形

在 x=±n λ /2(n=0,1,2,3,…)处,满足 2πkx=±nπ的条件时,各点的振幅为零,就
是波节的位置。
上式为一维驻波的波函数。而话筒的膜片等振动可以看成二维驻波,这些驻波分布在平面
或曲面上。一块四周固定的矩形板的振动是最简单二维驻波,如图 2 所示,它的波函数也可以
表示为一位置函数 Ψ (x,y)与时间函数 f(t)这两部分的乘积。从 x 方向看,膜片的振动可以
但与弦线的情况不同,它们不等于一个基频的整数倍。膜的本征频率与边界条件等许多因素有
关,情况很复杂,本实验不再展开论述。图 3 是克拉尼板显示的一个克拉尼(二维驻波)图形。
图 2 矩形膜
图 3 一种克拉尼图形
实验仪器 图 4 为一台 XD7 型正弦波信号发生器的示意图。该信号发生器能输出频率范围从 20Hz 到
形时所对应的频率,在纸上画出几个典型的克拉尼图形,完成表格内容。 3.写出出现克拉尼图形的频率范围。
观察思考 1.弦线的松紧程度对驻波的波节数及传播速度有何影响? 2.在弹奏弦线乐器时,发出声音的音调与弦线的长度、粗细、松紧程度有什么关系?为什
么? 3.克拉尼图形与所使用的压电陶瓷片数量以及贴在板上位置是否有关? 4.是否可以用食盐代替细砂进行克拉尼图形实验? 5.克拉尼板的厚度及均匀性对克拉尼图形是否有影响?
3.改变信号发生器输出频率,当出现 5 个完整波腹时,测出此时的半波长 λ /2,根据以上
实验得出的波速计算出电压信号的频率ν2,并与信号发生器发出的信号频率ν20 相比较.完成 表格内容。
4.把弦线放长、拉长或缩短,根据驻波半波长、电压信号频率计算出传播速度,并讨论波 的弦线上的传播速度与弦线长度及其松紧程度的关系。
砝码。打开信号发生器,频段旋钮至 1 档,输出衰减旋钮至 8Ω 档,使振源振动。从低到高调 节信号发生器输出频率,当出现驻波时,观察弦线上的驻波的波节数,并观察驻波的波节数增 减。
驻波

四 驻波的能量 位移最大时 波 节 波 腹 A B C
x x
平衡位置时
∂y 2 dWp ∝ ( ) ∂x
∂y 2 dWk ∝ ( ) ∂t
驻波的能量在相邻的波腹和波节间往复变化, 驻波的能量在相邻的波腹和波节间往复变化, 在相邻的波节间发生动能和势能间的转换,动能 在相邻的波节间发生动能和势能间的转换, 主要集中在波腹,势能主要集中在波节, 主要集中在波腹,势能主要集中在波节,但无长 距离的能量传播. 距离的能量传播
觉和底片感光上起主要作用 . 真空中的光速
r E = E 0 cos ω (t − ) u r H = H 0 cos ω (t − ) u
c=
1
ε 0 µ0
14 14
可见光的范围
λ : 400 ~ 760nm ν : 7.5 × 10 ~ 4.3 × 10 Hz
二 相干光 1)普通光源的发光机制 ) 激 发 态 1 2 P
y 2 = A cos 2π (ν t +
x
λ
)
)
x
y = y1 + y 2
= A cos 2π (ν t − x
λ
λ x = 2 A cos 2π cos 2π ν t λ
驻波的振幅 与位置有关
) + A cos 2π (ν t +
x
λ
)
各质点都在作同 频率的简谐运动
讨论
cos 2 π ν t 驻波方程 y = 2 A cos 2 π λ x 1)振幅 2 A cos 2 π 随 x 而异, 与时间无关 而异, 与时间无关. )
λ
cos 2 π x =
1 0
x
2π
x
驻波形成的条件

驻波形成的条件 驻波是指两列振幅相同的相⼲波在同⼀直线上沿相反⽅向传播时互相叠加⽽成的波,对于形成驻波的条件和特点,很多⼈都不太了解。
下⾯由店铺为你详细介绍驻波的相关知识。
形成驻波的条件 ⼀弦线的⼀端与⾳叉⼀臂相连,另⼀端经⽀点O并跨过滑轮后与⼀重物相连。
⾳叉振动后在弦线上产⽣⼀⾃左向右传播的⾏波,传到⽀点O后发⽣反射,弦线中产⽣⼀⾃右向左传播的反射波,当弦长接近1/2波长的整数倍时。
两列波叠加后弦线上各点的位移为(设⾳叉振动规律为u=Acosωt)u(x,t)=2Asin(x)sin(ωt)=A(x)sin(ωt),弦线上每个固定的点均作简谐运动,但不同点的振幅不同,由x值决定。
振幅为零的点称为波节,振幅最⼤处称为波腹。
波节两侧的振动相位相反。
相邻两波节或波腹间的距离都是半个波长。
在⾏波中能量随波的传播⽽不断向前传递,其平均能流密度不为零;但驻波的平均能流密度等于零,能量只能在波节与波腹间来回运⾏。
两列振幅相同的相⼲波在同⼀直线上沿相反⽅向传播时互相叠加⽽成的波,称为驻波。
驻波的特性 ⼊射波(推进波)与反射波相互⼲扰⽽形成的波形不再推进(仅波腹上、下振动,波节不移动)的波浪,称驻波。
驻波多发⽣在海岸陡壁或直⽴式⽔⼯建筑物前⾯。
紧靠陡壁附近的海⽔⾯随时间虽作周期性升降,海⽔呈往复流动,但并不向前传播,⽔⾯基本上是⽔平的,这就是由于受岸壁的限制使⼊射波与反射波相互⼲扰⽽形成的。
波⾯随时间作周期性的升降,每隔偶数个半个波长就有⼀个波⾯升降幅度为最⼤的断⾯,称为波腹;当波⾯升降的幅度为0时的断⾯,称为波节。
相邻两波节间的⽔平距离仍为半个波长,因此驻波的波⾯包含⼀系列的波腹和波节,腹节相间,波腹处的波⾯的⾼低虽有周期性变化,但此断⾯的⽔平位置是固定的,波节的位置也是固定的。
这与进⾏波的波峰、波⾕沿⽔平⽅向移动的现象正好相反,驻波的形状不传播,故名驻波。
当波⾯处于最⾼和最低位置时,质点的⽔平速度为零,波⾯的升降速度也为零;当波⾯处于⽔平位置时,流速的绝对值最⼤,波⾯的升降也最快,这是驻波运动独有的特性。
大学物理实验弦线上的驻波

使 用
砝码质量
2. 电动音叉振动频的率测定
学
11 级
弦线线密度: = 0.4488 103 kg/m 砝码质 量 (g) 张力 F (N) 半波数 目 n
南京地区重力加速度:_________________
2L / n
20
供
仅
3. 驻波波长的测定 弦线长度 / cm 半波数目 (个) (λ/2)/ cm
1
东
南
相位是一个很重要的物理概念,我们将在《大学物理》课程中介绍。可参阅有关教材。
大
学
成
贤 学
院
实验原理
物
理
实 验
级
中
心
波节,弦线与音叉脚相连接处也可以近似地看做波节。 研究指出,相邻两波节之间的距离为波长的一半,即有 2L 所以,只有当弦线的长度 l 为半波长 /2 的整数倍时才能形成稳定的驻波。这也就是说,要 想在弦线上出现稳定驻波的条件是
使 用 学 生 成 贤 学 院 物 理 实
实验内容
1. 定性观察弦线上的驻波现象
(1) 装好仪器, 移动音叉使弦线长约为 120cm。 在弦线一端的砝码托上加 20 克砝码 (连 定的驻波,并使振幅最大。
(2)前后移动音叉,使驻波波形清晰,观察弦线上的驻波的波节数。前后移动音叉, 把弦线放长、拉长或缩短,观察弦线上的驻波形成与弦线长度及其松紧程度的关系,并观察 驻波波节数的增减。
弦线上的振动
驻波是由两列传播方向相反而振幅、频率都相同,且相位差 1 恒定的简谐波波叠加而成 的。驻波有一维驻波、二维驻波等。例如,按某些频率激发弦乐器的弦线振动,弦线就会形 成一维驻波。对于话筒的膜片、锣鼓鼓面,它们形成的驻波分布在平面或曲面上,这是二维 驻波。驻波在声学、光学、无线电工程等方面都有广泛的应用。
5驻波

1
•如果 •如果
2
2u2 1u1 2u2 1u1
界面处出现半波损失;则介
质1称为波疏媒质,介质2称为波密媒质。 界面处不出现半波损失;则介 质1称为波密媒质,介质2称为波疏媒质。
2.相位突变
界面处为波节时,反射波相位突变了,相当半 个波长的波程----半波损失。
11
五、弦线上驻波形成条件
§ 5.6
驻波
1
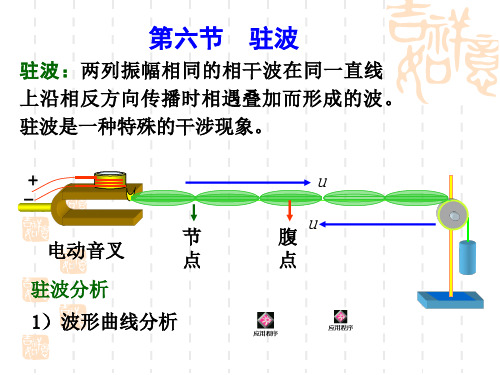
一、驻波
1.驻波的产生 驻波是两列振幅、频率和传播速率都相同的相干 波在同一直线上沿相反方向传播时波的叠加而形成的现 象。(由于其波动看起来处于静止状态,与行波相对称 为驻波。) 当一列波遇到障碍时产生的反射波与入射波叠加 可产生驻波----波形不传播。
2
二 、驻波方程
t x 正行波(入射波) y1 A cos2 T t x 负行波(反射波) y2 A cos2 T
合成波 由三角公式:
y y1 y2
cosα+cosβ=2cos[(α+β)/2]cos[ (α-β)/2]
t x t x y A cos2 A cos2 T T
t 2 A cos 2 cos 2 T
4.波节、波腹位置 ①.波节位置
波腹
x 0
2 A cos 2
2
x
(2k 1)2x (2k 1)
4
( k 0,1,2)
5
/2
波节
②.相邻波节距离
波腹
x (2k 1)
4
x k1 x k [2( k 1) 1] (2k 1) 4 4 2 x cos 2 1 ③.波腹位置
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
19
波节
4
3.波腹 振幅始终最大的位置。 波腹----振幅始终最大的位置 波腹
波节
4.波节、波腹位置 波节、 波节 ①.波节位置 波节位置
波腹 x =0
2 A cos 2π
2π
x
λ
λ
= ±(2k + 1)
π
2
( k = 0,1,2L)
5
x = ±(2k + 1)
λ
4
λ /2
波节
②.相邻波节距离 相邻波节距离
λ
2
④.相邻波腹距离 相邻波腹距离
x k +1 − x k = ( k + 1) − k = 2 2 2
λ
λ
λ
7
λ /2
λ /2
λ /4
波节
波腹
波节与波腹之间的距离为 λ / 4 除波节、波腹外,其它各点0<振幅<2A 5.驻波的波形、能量都不能传播,驻波不是波,是一种特殊的 驻波的波形、 驻波的波形 能量都不能传播,驻波不是波, 振动。 振动。 6.波节两侧的振动相位相反。(任意的一个瞬间,波形与行波 波节两侧的振动相位相反。(任意的一个瞬间, 波节两侧的振动相位相反。(任意的一个瞬间 的波形相同) 的波形相同)
S
vs
因为波源所发出的相邻的两个位 相相同的波面是在不同地点发出 的,这两个地点相隔的距离为 vsT。 式中T 为波源的周期。因此观察 者听到的声音波长被压缩。
vsT
λ'
λ ' = λ − vsT = (u − vs )T =
u − vs
ν
(3)
15
λ ' = λ − vsT = (u − vs )T =
cosα+cosβ=2cos[(α+β)/2]cos[ (α-β)/2]
t x t x y = A cos 2π − + A cos 2π + T λ T λ
t = 2 A cos 2π cos 2π λ T
x
3
驻波方程
u ν1 = ν u + vs
反射面接收到的是以vs向它接近的 波源的频率;反射面不动所以反 射面入射频率等于反射频率。
反射面 声源
A S Vs
观察者
u ν2 = ν u − vs
拍频
2v s u u ∆ν = ν− ν = 2 2 uν u − vs u + vs u − vs
18
改写为: u 2 − vs2 = 2uνvs ∆ν 2uνvs 2 vs + − u2 = 0 ∆ν vs=0.25m/s
§ 2-7.
驻波
1
一、驻波
1.驻波的产生 驻波是两列振幅、 驻波是两列振幅、频率和传播速率都相同的相干 波在同一直线上沿相反方向传播时波的叠加而形成的现 。(由于其波动看起来处于静止状态 由于其波动看起来处于静止状态, 象。(由于其波动看起来处于静止状态,与行波相对称 为驻波。) 为驻波。) 当一列波遇到障碍时产生的反射波与入射波叠加 可产生驻波----波形不传播 波形不传播。 可产生驻波 波形不传播。
vs
λ’由(3)式确定。
u − vR u − vR ν '= = ν λ' u − vs ( 4)
vsT
λ'
16
u − vR u − vR ν '= = ν λ' u − vs
上述公式当vs等于0时,就是(1)式。
u − vR ν '= ν u
u ν '= ν u − vs
上述公式当vR等于0时,可以化为(3)式。
ν’是观察者听到的频率, ν’=u/λ’ (λ’是压缩了的波 长。) u u u − vs ν '= = ν λ'= (3) λ ' u − vs ν 由上面的 计算可以看出vR、 vs的影响是不同的。
Hale Waihona Puke 17例1 :一声源振动的频率为2040赫兹,以速度vs向一反射面接近, 观察者在A处测得拍音的频率3赫兹,如声速为340米/秒,求波 源移动的速度? 解:1.到达观察者处的频率有:直接从 远离它的波源来的声音ν1 和经反射面反 射后的频率ν2,两者形成拍。
由 u = λν λ 代入 l = k 2
当弦长为 l = k
λ
l = λ /2 l=λ
当ν
u ν =k 2l u 为 的整数倍的波才能形成驻波。 的整数倍的波才能形成驻波。 2 l
12
多普勒效应
多普勒效应是由于波源与观测者的相对运动而产生的一种物 理现象。
感受到频率的变化的原因在于相对运动。 1、相对于媒质,波源和观察者都不动的情况。 2、相对于媒质,波源不动,观察者以速度vR向着或远离波 源运动。 3、相对于媒质,观察者不动,波源以速度vs向着或背向观 察者运动。 4、相对于媒质,波源和观察者同时运动 以下分别不同情况加以讨论:
波腹
x = ±(2k + 1)
λ
4
x k +1 − x k = [ 2( k + 1) + 1] − (2k + 1) = 4 4 2 x cos 2π = 1 ③.波腹位置 波腹位置
λ
λ
λ
λ
6
λ /2
λ /2
波节 x 2π = ± kπ
波腹 振幅为2A 振幅为
( k = 0,1,2L)
λ
x = ±k
ν
频率升高
vs = 0
若观察者以速度 vR 离开波源运动, 同理可得观察者接受到的频率:
u
− vR
14
ν '=
u − vR u
ν 频率降低。 频率降低。
当:波源不动,观察者也不动。波长由: λ = uT = ν 3、相对于媒质:观察者不动,波源以速度 vs 向着观察者运动。
u
uT
S
v
vsT
λ
λ '
u − vs
ν
u − vs = λ u
(3)
如果波源是背着观察者运动的,则波长被拉开。拉长的距离比 现在媒质中的波长增加vsT。 3、若观察者与波源同时运动, 可以认为观察者在一个波长被 压缩的声场中运动,利用1式
vR
S
ν '=
u − vR
u − vR ν '= λ'
λ
u − vR = ν u
(1)
10
ρ1
•如果 如果
ρ2
ρ 2u2 > ρ1u1 ρ 2u2 < ρ1u1
界面处出现半波损失; 界面处出现半波损失;则介 出现半波损失
称为波疏媒质, 称为波密媒质。 质1称为波疏媒质,介质 称为波密媒质。 称为波疏媒质 介质2称为波密媒质 •如果 如果 界面处不出现半波损失; 界面处不出现半波损失;则介 不出现半波损失
7.两波节间同步振动。 两波节间同步振动。 两波节间同步振动
8
播放教学片 CD2
驻波
9
四、半波损失
对于弦线上的驻波,反射端被作用力约束, 对于弦线上的驻波,反射端被作用力约束,不能 运动。 运动。从数学的观点看也可以认为反射波在约束 点发生半个波长的位相移动,称为半波损失。 点发生半个波长的位相移动,称为半波损失。 y入 = A cos(ω t + φ ) y反 = A cos(ω t + φ ' ) ∆φ = φ − φ’ π = y = y入 + y反 = 0 λ/2 y反 = A cos(ω t + φ + 2π ) λ 1.半波损失条件 当波从波疏媒质进入波密媒质, 当波从波疏媒质进入波密媒质,并在与波密媒质的交 界处反射时,反射波存在半波损失, 界处反射时,反射波存在半波损失,相位突变π。
t y = 2 A cos 2π cos 2π λ T
x
三、讨论
有关, x 只与位置 x 有关,而与时间 t 1.振幅项 2 A cos 2π 振幅项 无关。最后一项只和时间有关, λ 无关。最后一项只和时间有关, 表明各质点做幅度确定的简谐 振动。 振动。 2.波节 振幅始终为 0 的位置。 波节----振幅始终为 的位置。 波节
13
λ 2、相对于媒质,波源不动,取u的传播方向为正方向。 观察者以速度vR向着波源运动。
1、相对于媒质,波源不动,观察者也不动。
ν=
u
u − vR u − vR ν '= + = = ν uν u λ λ u
因为此时波源的频率就是波的频率 当观察者向着波源运动时
− vR
(1)
λ
S
ν '=
u + vR u
2
二 、驻波方程
t x 正行波(入射波) 正行波(入射波) y1 = A cos2π − T λ t x 负行波(反射波) 负行波(反射波) y2 = A cos2π + T λ
合成波 由三角公式: 由三角公式:
y = y1 + y2
称为波密媒质, 称为波疏媒质。 质1称为波密媒质,介质 称为波疏媒质。 称为波密媒质 介质2称为波疏媒质
2.相位突变
界面处为波节时, 界面处为波节时,反射波相位突变了π,相当半 个波长的波程----半波损失。 个波长的波程 半波损失。 半波损失
11
五、弦线上驻波形成条件
2 才能形成驻波。 才能形成驻波。
