高一数学方程的根与函数的零点测试题
高一数学函数与方程试题

高一数学函数与方程试题1.已知一元二次方程的两个实根为,且,则的取值范围是()A.B.C.D.【答案】A【解析】由程的二次项系数为1>0,故函数图象开口方向朝上又∵方程的两根满足0<x1<1<x2,则,即,即其对应的平面区域如下图阴影示:∵表示阴影区域上一点与原点边线的斜率,由图可知∈故选A.【考点】一元二次方程的根的分布与系数的关系;线性规划.2.函数的图象与轴的交点个数是()A.4B.3C.1D.0【答案】B.【解析】首先将函数化简为,然后根据函数与方程的关系知,要求“函数的图像与轴的交点的个数”就转化为求“方程的实数根的个数”,于是对其进行分类讨论:①当时,令,解得,,此时方程有两个实数根满足题意;②当时,令,解得,,因为,不满足,故舍去,所以此时方程有且仅有一个实数根满足题意. 综上所述,方程的实数根的个数有3个,即函数的图像与轴的交点的个数有3个,故选B.【考点】函数与方程.3.一艘船上午在A处,测得灯塔S在它的北偏东300处,且与它相距海里,之后它继续沿正北方向匀速航行,上午到达B处,此时又测得灯塔S在它的北偏东750,此船的航速是()海里/小时。
A.B.C.D.【答案】D【解析】由题意得在三角形中,,由正弦定理得,即,得,因此航行的速度.【考点】正弦定理在三角形中的应用.4.函数的零点个数为.【答案】【解析】函数的零点,就是方程的根,转化为与的图象交点的横坐标,结合图象知有两个交点,故零点个为2个.【考点】函数的零点,数形结合的数学思想.5.方程的解所在的区间是()A.B.C.D.【答案】C【解析】设,则由指数函数与一次函数的性质可知,函数与的上都是递增函数,所以在上单调递增,故函数最多有一个零点,而,,根据零点存在定理可知,有一个零点,且该零点处在区间内,故选答案C.【考点】函数与方程.6.二次函数中,,则函数的零点个数是()A.0个B.1个C.2个D.无法确定【答案】C【解析】令=0,二次函数的零点就是相应一元二次方程的根。
高一上学期数学人教A版必修第一册第四章《指数函数与对数函数》函数的零点与方程的解(二)同步练测

4.5.1函数的零点与方程的解(二)同步练测考试时间:120分钟满分:150分一、单选题:本大题共8小题,每个小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.A .(]4,16B .[)4,+∞C .(),4-∞-D .[)16,4--二、多选题:本大题共4小题,每个小题5分,共20分.在每小题给出的选项中,只有一项或者多项是符合题目要求的.三、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上.四、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.参考答案:1.B【解析】由题意知,αβ是二次函数236y x x =+-的两个零点,故,αβ是2360x x +-=的两个根,则2360αα+-=,且+3αβ=-,则236αα+=且3βα=--,故22233(3)5αβαααα-=-++=+-=-=,故选:B 2.B【解析】令()ln 24f x x x =+-,显然()ln 24f x x x =+-单调递增,又因为()12420f =-=-<,()2ln 244ln 20f =+-=>,由零点存在性定理可知:()ln 24f x x x =+-的零点所在区间为()12,,所以ln 42x x =-的根所在区间为()12,.故选:B 3.B【解析】函数()23x f x x a =++在区间(0,1)内存在零点,且函数在定义域内单调递增,由零点存在性定理知(0)(1)0f f ⋅<,即()()150a a ++<,解得51a -<<-所以实数a 的取值范围是(5,1)--,故选:B 4.A【解析】要使函数()()g x f x a =-有三个零点,则()f x a =有三个不相等的实根,即()f x 与y a =的图象有三个交点,当1x ≤-时,()113x f x +=-在(],1-∞-上单调递减,[)()0,1f x Î;当10-<≤x 时,()131x f x +=-在(]1,0-上单调递增,(]()0,2f x Î;当0x >时,()ln f x x =在()0,∞+上单调递增,()f x ∈R ;由()f x 与y a =的图象有三个交点,结合函数图象可得()0,1a ∈,故选:A.由图像可知01a b <<<<由()()f a f b =得lg a =联立2y x y x =⎧⎨=-⎩,得由图象可知,直线9.BCf x对应的二次方程根的判别式【解析】函数()可观察出①当1a >时,方程(f ()220()xf a a R --=∈有方程()1f t =-的解为1(0,1)t t =∈,2(,0)t t =∈-∞,即1()f x t =,2()f x t =,在同一坐标系中作出函数()y f x =和1y t =,2y t =的图象,由图可知函数()y f x =和1y t =,2y t =有4个交点,所以函数[()]1y f f x =+有4个零点.当0a ≤时,方程()1f t =-的解为3(0,1)t t =∈,即3()f x t =,在同一坐标系中作出函数()y f x =和3y t =的图象,由图可知函数()y f x =和3y t =有1个交点,所以函数[()]1y f f x =+有1个零点.故选:AD13.1【解析】解法一:令()0f x =,可得方程2ln 30x x +-=,即2ln 3x x =-,故原函数的零点个数即为函数ln y x =与23y x =-图象的交点个数.在同一平面直角坐标系中作出两个函数的大致图象(如图).由图可知,函数23y x =-与ln y x =的图象只有一个交点,故函数()2ln 3f x x x =+-只有一个零点,故答案为:1解法二:∵()21ln11320f =+-=-<,()22ln 223ln 210f =+-=+>,∴()()120f f <,又()2ln 3f x x x =+-的图象在()1,2上是不间断的,∴()f x 在()1,2上必有零点,又()2ln 3f x x x =+-在()0,∞+上是单调递增的,∴函数()f x 的零点有且只有一个,故答案为:114.(]()1,34,+∞ 【解析】由于4y x =-在R 上只有一个零点4,函数243y x x =-+在R 上的两个零点为1和3,若4λ>,此时4y x =-在x λ≥上没有零点,函数243y x x =-+在x λ<上的两个零点为1和3,满足题意,当34λ<≤时,此时4y x =-在x λ≥上有零点4,函数243y x x =-+在x λ<上有零点为1和3,不满足题意,舍去当13λ<≤时,此时4y x =-在x λ≥上有零点4,函数243y x x =-+在x λ<上有零点为1,满足题意,当1λ≤时,此时4y x =-在x λ≥上有零点4,函数243y x x =-+在x λ<上没有零点,不满足题意,舍去,因为函数()12xf x ⎛⎫= ⎪⎝⎭点212,log x x ⎛⎫ ⎪⎝⎭与点⎛⎝由图象可知,-当0a >时,12116a a <<,解得111612a <<;当a 11,⎛⎫⎧⋃。
方程的根与函数的零点(5)

x2 2x 3 0
y x2 2x 3
透数形结合 的思想。为
方程的根 函数值y=0时的x的值 函数图象与x轴交点的横坐标
板书
引入函数零 点的概念打 下基础。
2019/6/26
27
五、教学过程
(三)数形结合,巩固认识
若将上面特殊的一元二次方程推广到一般的一元二
次 方 程 ax2 bx c 0 (a 0) 及 相 应 的 二 次 函 数
一些复杂的方程无法 求解,造成学生的认 知冲突,引发学生的好 奇心和求知欲。此时 开门见山的提出用函 数的思想解决方程根 的问题,点明本节课的 课题。
2019/6/26
25
五、教学过程
(二)启发引导,逐步深入
设计意图
问题2:
以问题激发学生
一元二次方程ax2+bx+c=0(a≠0)
思考,将大问题
分解为几个小问 与二次函数y=ax2+bx+c(a≠0)有什么联系? 题,自然地得到
2019/6/26
3
方程
函数 函 数 的 图 像
x2-2x-3=0 x2-2x+1=0 x2-2x+3=0 y= x2-2x-3 y= x2-2x+1 y= x2-2x+3
y
.
.
2
.1 .
-1 0 1 2 3 x -1
-2 -3
. -4
y
.2
.
1. .
. -1 0 1 2
x
y
.5 4
.
3.
2
.
.
1
-1 0 1 2 3 x
方程的实数根 x1=-1,x2=3
2022版新教材数学人教A版必修第一册基础训练-4.5.1-函数的零点与方程的解-含解析

课时评价作业基础达标练1.(2021安徽合肥高一期末)函数f(x)=lg|x| 的零点是( ) A.(1,0)B.(1,0)和(-1,0) C.1D.1和-1 答案: D2.已知函数f(x)={ln(x −1),x >1,2x−1−1,x ≤1, 则f(x) 的零点个数为( )A.0B.1C.2D.3 答案: C3.(2021广东广州高一期末)函数f(x)=(x 2−1)√x 2−4 的零点个数是( ) A.1B.2C.3D.4 答案: B4.(多选)下列关于方程x 3+x 2−2x −1=0 的说法正确的是( ) A.在(-2,-1)内有根 B.在(-1,0),0)内有根 C.在(1,2)内有根D.在(−∞,+∞) 内没有实数根 答案: A ; B ; C解析:设f(x)=x 3+x 2−2x −1 .分别计算f(−2),f(−1),f(0),f(1),f(2) 的值,再根据函数零点存在定理判断.5.已知0<a <1 ,则函数y =a |x|−|log a x| 的零点个数为( ) A.1B.2C.3D.4 答案: B解析:函数y =a |x|−|log a x|(0<a <1) 的零点的个数即方程a |x|=|log a x|(0<a <1) 的解的个数,也就是函数f(x)=a |x|(0<a <1) 与g(x)=|log a x|(0<a <1) 的图象的交点的个数.画出函数f(x)=a |x|(0<a <1) 与g(x)=|log a x|(0<a <1) 的图象(如图所示),观察得出结论.6.已知函数则函数f(x)={2x −1,x ≤1,log 12x +2,x >1, 则函数f(x) 的零点为 .答案: 0或47.若abc ≠0 且b 2=ac ,则函数f(x)=ax 2+bx +c 的零点个数是 . 答案: 08.已知y =x(x −1)(x +1) 的图象如图所示.令f(x)=x(x −1)⋅(x +1)+0.01 ,则下列关于f(x)=0 的叙述正确的是 (填序号).①有三个实根;②当x >1 时恰有一个实根; ③当0<x <1 时恰有一个实根; ④当−1<x <0 时恰有一个实根; ⑤当x <−1 时恰有一个实根. 答案: ①⑤解析: f(x) 的图象是将函数y =x(x −1)⋅(x +1) 的图象向上平移0.01个单位长度得到的,故f(x) 的图象与x 轴有三个交点,它们分别在区间(−∞,−1),(0,12) 和(12,1) 内,故只有①⑤正确.9.判断下列函数的零点个数: (1)f(x)=x 3−3x 2−2x +6 ; (2)f(x)=2x +lg(x +1)−2 .答案: (1)f(x)=x 3−3x 2−2x +6=x 2(x −3)−2(x −3)=(x 2−2)(x −3) ,令f(x)=0 ,则x =±√2 或x =3 ,所以函数有三个零点.(2)令ℎ(x)=2−2x ,g(x)=lg(x +1) ,在同一平面直角坐标系中作出ℎ(x)=2−2x 和g(x)=lg(x +1) 的图象.由图可知,g(x)=lg(x +1) 的图象和ℎ(x)=2−2x 的图象有且只有一个交点,即f(x)=2x +lg(x +1)−2 有且只有一个零点.10.关于x 的方程mx 2+2(m +3)x +2m +14=0 有两个实数根,且一个大于4,一个小于4,求m 的取值范围.答案: 令f(x)=mx 2+2(m +3)x +2m +14 ,依题意得{m >0,f(4)<0 或{m <0,f(4)>0,即{m >0,26m +38<0 或{m <0,26m +38>0, 解得−1913<m <0 ,所以m 的取值范围是(−1913,0) .素养提升练11.(2020山西忻州一中高一期中)已知函数f(x)={log 2(1−x),x ≤0,−x 2+4x,x >0, 则函数g(x)=f[f(x)]−1 的零点个数为( ) A.4B.7C.8D.9 答案: B解析:令g(x)=0,f(x)=t ,则f(t)=1 , 当t ≤0 时,log 2(1−t)=1 ,解得t =−1 ; 当t >0 时,−t 2+4t =1 ,解得t =2±√3 . 故f(x)=−1 或f(x)=2+√3 或f(x)=2−√3 . 当x ≤0 时,令log 2(1−x)=−1 ,解得x =12 ,舍去; 令log 2(1−x)=2+√3 ,解得x =1−22+√3 ; 令log 2(1−x)=2−√3 ,解得x =1−22−√3 .当x >0 时,令−x 2+4x =−1 ,解得x =2+√5 ,x =2−√5 (舍去); 令−x 2+4x =2+√3 ,整理得x 2−4x +2+√3=0 , 解得x =2+√6−√22或x =2−√6−√22;令−x 2+4x =2−√3 ,整理得x 2−4x +2−√3=0 ,解得x =2+√2+√62或x =2−√2+√62.综上所述,函数零点有1−22+√3,1−22−√3,2+√5,2±√6−√22,2±√2+√62,共7个.故选B.12.已知函数f(x)={−x 2+1,x ≤0,|x −2|,x >0, 若关于x 的方程[f(x)]2−af(x)=0 有且只有3个不同的实数根,则实数a 的取值范围是 . 答案: (−∞,0)∪[2,+∞) 解析: 由题意可知,f(x)={−x 2+1,x ≤0,|x −2|,x >0={−x 2+1,x ≤0,−(x −2),0<x <2x −2,x ≥2.,函数f(x) 的大致图象如图:∵ 关于x 的方程[f(x)]2−af(x)=0 有且只有3个不同的实数根, ∴f(x)⋅(f(x)−a)=0 有且只有3个不同的实数根, 即f(x)=0 与f(x)=a 一共有3个不同的实数根,∵ 当f(x)=0 时,有x =−1 与x =2 两个实数根,∴f(x)=a 有且只有1个实数根, ∴a <0 或a ≥2 .∴ 实数a 的取值范围是(−∞,0)∪[2,+∞) .13.已知二次函数f(x) 满足f(0)=3,f(x +1)=f(x)+2x . (1)求函数f(x) 的解析式;(2)令g(x)=f(|x|)+m(m ∈R) ,若函数g(x) 有4个零点,求实数m 的取值范围. 答案: (1)设f(x)=ax 2+bx +c(a ≠0) ,∵f(0)=3,∴c =3,∴f(x)=ax 2+bx +3 ,∴f(x +1)=a(x +1)2+b(x +1)+3=ax 2+(2a +b)x +a +b +3 , f(x)+2x =ax 2+(b +2)x +3 , ∵f(x +1)=f(x)+2x ,∴{2a +b =b +2,a +b +3=3, 解得a =1,b =−1 , ∴f(x)=x 2−x +3 .(2)由(1)得g(x)=x 2−|x|+3+m ,在平面直角坐标系中画出函数g(x) 的图象,如图所示,由于函数g(x) 有4个零点,故函数g(x) 的图象与x 轴有4个交点. 由图象得{3+m >0,114+m <0, 解得−3<m <−114 ,即实数m 的取值范围是(−3,−114) .创新拓展练14.(多选)对于函数f(x) 和g(x) ,设α∈{x|f(x)=0},β∈{x|g(x)=0} ,若存在α,β 使得|α−β|≤1 ,则称f(x) 与g(x) 互为“零点相邻函数”.若函数f(x)=e x−1+x −2 与g(x)=x 2−ax −a +3 互为“零点相邻函数”,则实数a 的取值可以是( )A.2B.73C.3D.4答案:A; B; C解析:易知函数f(x)=e x−1+x−2是R上的增函数,且f(1)=0,则α=1,结合“零点相邻函数”的定义可得|1−β|≤1,则0≤β≤2,故函数g(x)=x2−ax−a+3在区间[0,2]上存在零点,即方程x2−ax−a+3=0在区间[0,2]上存在实数根,整理可得a=x 2+3x+1=x2+2x+1−2x−2+4x+1=(x+1)+4x+1−2,令ℎ(x)=(x+1)+4x+1−2,根据对勾函数的性质知函数ℎ(x)在区间[0,1)上单调递减,在[1,2]上单调递增,又ℎ(0)=3,ℎ(2)=73,ℎ(1)=2,则函数ℎ(x)的值域为[2,3].故实数a的取值范围是[2,3],故选ABC.。
高一数学二次函数根的分布专题归类精练
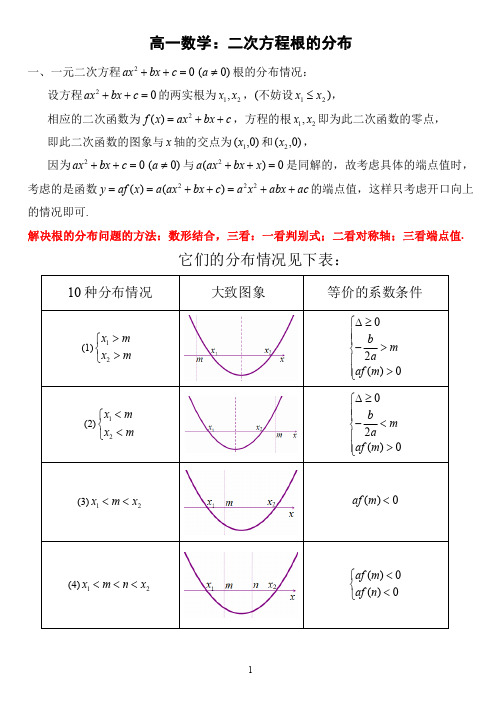
高一数学:二次方程根的分布一、一元二次方程02=++c bx ax )0(≠a 根的分布情况:设方程02=++c bx ax 的两实根为12,x x ,(不妨设21x x ≤),相应的二次函数为c bx ax x f ++=2)(,方程的根12,x x 即为此二次函数的零点, 即此二次函数的图象与x 轴的交点为)0,(1x 和)0,(2x ,因为02=++c bx ax )0(≠a 与0)(2=++x bx ax a 是同解的,故考虑具体的端点值时,考虑的是函数ac abx x a c bx ax a x af y ++=++==222)()(的端点值,这样只考虑开口向上的情况即可.解决根的分布问题的方法:数形结合,三看:一看判别式;二看对称轴;三看端点值.它们的分布情况见下表:如上图,只是可以过两端点,注注2:对于端点值是否可取,最好单独讨论;注3:以上11种情况都有相应的等价形式,对于具体题中的条件,往往是几种情况合在一起的,这时需要分类讨论,此时莫忘注1,注2 .特别注意下列两种情况:一. 函数)(x f 在()n m ,内仅有一个零点,可分:(1)方程0)(=x f 有且只有一根(两根重合时),且这个根在区间()n m ,内,即0∆=, 此时由0∆=可以求出参数的值,然后再将参数的值带入方程,求出相应的根, 检验根是否在给定的区间内,如若不在,舍去相应的参数的值.(2)若()0f m =,可以确定的求出相应的系数(或得到一个关系),从而可以求出另外一根, 若这另外的一根在区间()n m ,内,则满足条件;若不在,则这种情况不成立.(3)若()0f n =时,同理.(4)以上三种都讨论完了,只剩下一种情况,即只要0)()(<n f m f 即可.例1:已知624)(2++-=m mx x x f 在区间()3,0-内有且仅有一个零点,求m 的取值范围.解:①当0∆=时,即()2164260m m -+=,得出1m =-或32m =, 当1m =-时,根()23,0x =-∈-,即1m =-满足题意; 当32m =时,根()33,0x =∉-,故32m =不满足题意; ②当0151462129)3(=+=+++=-m m m f ,解得:1415-=m , 由韦达定理的两根之积为72767156232=+-=+=⨯-m x , 即)0,3(792-∈-=x ,满足条件,故1415-=m 合适; ③当062)0(=+=m f ,解得:3-=m ,由韦达定理的两根之和为12402-==+m x , 即)0,3(122-∉-=x ,不满足条件,故3-=m (舍);④当0)0()3(<⋅-f f 时,即0)62)(1514(<++m m ,得出14153-<<-m ,必满足条件. 综上所述所求m 的取值范围是:14153-≤<-m ,或1m =-. 注:你能发现这个题的巧解吗?二. 函数)(x f 在],[n m 内仅有一个零点,可同上分析.即先讨论0=∆(即方程两根重合)时的情况,验证相应的根是否合适;再看取到端点值时的情况,此时已知一根,由韦达定理易得另一根,验证是否满足条件;最后0)()(<n f m f 即可! 熟练之后,此次序可以灵活变通,只是请注意分类要不重不漏!例2:已知624)(2++-=m mx x x f 在区间]0,3[-内有且仅有一个零点,求m 的取值范围. 解:①当0∆=时,即()2164260m m -+=,得出1m =-或32m =, 当1m =-时,根]0,3[2-∈-=x ,即1m =-满足题意; 当32m =时,根]0,3[3-∉=x ,故32m =不满足题意; ②当0151462129)3(=+=+++=-m m m f ,解得:1415-=m , 由韦达定理的两根之积为72767156232=+-=+=⨯-m x , 即)0,3(792-∈-=x ,不满足条件,故1415-=m (舍);③当062)0(=+=m f ,解得:3-=m ,由韦达定理的两根之和为12402-==+m x , 即)0,3(122-∉-=x ,满足条件,故3-=m 合适;④当0)0()3(<⋅-f f 时,即0)62)(1514(<++m m ,得出14153-<<-m ,必满足条件. 综上所述所求m 的取值范围是:14153-<≤-m ,或1m =-. 注:你能发现这个题的巧解吗?注:讨论端点时,如果遇到下列情况,前参看下列题的处理办法!例3:已知方程02)2(2=++-x m mx 在区间()1,3上有一根,求m 的取值范围. 解:当0=m 时,易知方程仅有一个根为1,不满足条件当0≠m 时,令2)2()(2++-=x m mx x f ,因为()10f =, 所以()()()22212mx m x x mx -++=--,故另一根为2m, 由213m <<,得223m <<即为所求. 例4:已知方程02)2(2=++-x m mx 在区间]3,1[上有一根,求m 的取值范围. 解:当0=m 时,易知方程仅有一个根为1,满足条件;当0≠m 时,令)2)(1(2)2()(2--=++-=mx x x m mx x f ,必有一根为1 故另一根2m ,当12=m,即2=m 时合适; 否则必须满足:12<m 或32>m ,解得:0<m ,或320<<m ,或2>m综上所述,所求m 的取值范围是32<m 或2≥m .注:你能发现这两个题的巧解吗?以后再赘述吧,先抱歉了!二.根的分布经典题归类讲解例1、①m 取何实数值时,方程0)1(22=++-m x m x 有两个不等正实根.②m 取何实数值时,方程013422=-++m mx x 有两个负数根.③m 取何实数值时,关于x 的方程05)2(2=-+-+m x m x 的两个实根都大于2. 解:①令=)(x f m x m x ++-)1(22,其图像开口向上,对称轴为41+=m x , 判别式为168)1(22+-=-+=∆m m m m原条件⎪⎪⎩⎪⎪⎨⎧>=>+>+-=∆⇔0)0(0410162m f m m m 解得:2230-<<m 或223+>m ,即为所求.②令=)(x f 13422-++m mx x ,其图像开口向上,对称轴为m x -=, 判别式为)1)(21(16)2123(16)13(81622--=+-=--=∆m m m m m m . 原条件⎪⎪⎩⎪⎪⎨⎧>-=<-≥--=∆⇔013)0(00)1)(21(16m f m m m 解得:2131≤<m 或1≥m ,即为所求.③令=)(x f m x m x -+-+5)2(2,其图像开口向上,对称轴为21m x -=, 判别式为)4)(4(16)5(4)2(22-+=-=---=∆m m m m m .原条件⎪⎪⎩⎪⎪⎨⎧>+=-+-+=>-≥-+=∆⇔055424)2(2210)4)(4(m m m f m m m 解得:45-≤<-m ,即为所求.例2、①已知二次方程012)12(2=-+-+m mx x m 有一正根和一负根,求实数m 的取值范围.②已知二次函数33)42()2(2+++-+=m x m x m y 与x 轴有两个交点,一个在1=x 的左侧,一个在1=x 的右侧,求实数m 的取值范围.③m 取何实数值时,关于x 的方程05)2(2=-+-+m x m x 的一个实根大于2,另一个实根小于2.解:①令=)(x f 12)12(2-+-+m mx x m ,其图像开口方向不明,原条件0)1)(12()0()12(<-+=+⇔m f m ,解得:21->m . 即为所求. 注:利用两个之积012121<+-=m x x ,也可以快速得出!②令=)(x f 33)42()2(2+++-+m x m x m ,其图像开口方向不明,原条件0)12)(2()33422)(2()1()2(<++=++--++=+⇔m m m m m m f m , 解得:212-<<-m . 即为所求. 注:利用0)1)(1(21<--x x ,即021212422331)(2121<++=+++-++=++-m m m m m m x x x x 也可得.③令=)(x f m x m x -+-+5)2(2,其图像开口向上,原条件055424)2(<+=-+-+=⇔m m m f 解得:5-<m ,即为所求.注:利用0)2)(2(21<--x x ,即054)2(254)(22121<+=+---=++-m m m x x x x 也可得. 例3.①已知关于x 的方程:022=+-a ax x 有两个实根βα,,且满足2,10><<βα,求实数a 的取值范围.②已知关于x 的方程:062)1(22=-++--m m mx x m 有两个实根βα,,且满足βα<<<10, 求实数m 的取值范围.③已知关于x 的方程:0532=+-a x x 有两个实根βα,,且满足)3,1(),0,2(∈-∈βα,求实数a 的取值范围.解:①令=)(x f a ax x +-22,其图像开口向上,画图可得:原条件⎪⎩⎪⎨⎧<-=<-=>=⇔034)2(01)1(0)0(a f a f a f 解得:34>a ,即为所求.②令=)(x f 62)1(22-++--m m mx x m ,其图像开口方向不明,画图可得:原条件⎩⎨⎧<->-⇔0)1()1(0)0()1(f m f m ,即⎪⎩⎪⎨⎧<-++--->-+-⇔0)621)(1(0)6)(1(22m m m m m m m m即⎩⎨⎧<+-->+--⇔0)7)(7)(1(0)3)(2)(1(m m m m m m 解得:73-<<-m 或72<<m ,即为所求.③令=)(x f a x x +-532,其图像开口向上,画图可得:原条件⎪⎪⎩⎪⎪⎨⎧>+=+-=<-=+-=<=>+=++=-⇔0121527)3(022)1(0)0(0221012)2(a a f a a f a f a a f 解得:012<<-a ,即为所求.例4、①已知方程03222=+++m mx x 的两个不等实根都在区间)2,0(内,求实数m 的取值范围.②已知方程03222=+++m mx x 的两个不等实根都在区间]2,0[之外,求实数m 的取值范围. 解:令322)(2+++=m mx x x f ,其图像开口向上,对称轴为m x -=,由判别式0)3)(1(4)32(4)32(4422>-+=--=+-=∆m m m m m m ,得:1-<m 或3>m①的条件⎪⎪⎩⎪⎪⎨⎧>+=>+=<-<>∆⇔076)2(032)0(200m f m f m ,即⎪⎪⎪⎩⎪⎪⎪⎨⎧->-><<->-<⇔67230231m m m m m 或解得:167-<<-m 即为所求.②的条件可分为:两根都小于0,或两根都大于2,或一根小于0,一根大于2,三种情况故⎪⎩⎪⎨⎧>+=<->∆⇔032)0(00m f m 或⎪⎩⎪⎨⎧>+=>->∆076)2(20m f m 或⎩⎨⎧<+=<+=076)2(032)0(m f m f解得:3>m ,或无解,或23-<m ,故所求m 的取值范围是:23-<m 或3>m . 例5:已知集合}0107|{2≤+-=x x x A ,}05)2(|{2≤-+--=m x m x x B ,且A B ⊆, 求实数m 的取值范围.解:首先}52|{≤≤=x x A ;当∅=B 时,即不等式05)2(2≤-+--m x m x 无解,即0)5(4)2(2<---=∆m m 即:0162<-m ,解得:44<<-m ; -----(1)当∅≠B 时,即不等式05)2(2≤-+--m x m x 有解,其形式必为21x x x ≤≤; 其中21,x x 为方程05)2(2=-+--m x m x 的两个根,(不妨设21x x ≤) 按条件,只要5221≤≤≤x x 即可满足A B ⊆;按照根的分布的理论,此时只要满足:⎪⎪⎪⎩⎪⎪⎪⎨⎧≥-+--=≥-+--=≤-≤≥-=∆05)2(525)5(05)2(24)2(52220162m m f m m f m m即⎪⎪⎩⎪⎪⎨⎧-≥-≥-≤≤-≥-≤55284,4m m m m m 或,解得:45-≤≤-m ,-----(2)由(1)(2)可得:所求的m 的取值范围是45≤≤-m .三.自己练习巩固提升1.设有一元二次方程02)1(22=++-+m x m x .试问:(1)m 为何值时,有一正根、一负根.(2)m 为何值时,有一根大于1、另一根小于1. (3)m 为何值时,有两正根. (4)m 为何值时,有两负根.(5)m 为何值时,仅有一根在[1,4]内.2. 关于x 的方程012=-++a ax x 有异号的两个实根,求a 的取值范围.3.如果方程032)3(22=-+++a x a x 的两个实根中一根大于3,另一根小于3,求实数a 的取值范围. 4.若方程07)1(82=-+++m x m x 有两个负根,求实数a 的取值范围. 5. 关于x 的方程0422=-+-a ax x 有两个正根,求a 的取值范围.6.设关于x 的方程0)(44222=+++-n m x n m x 有一个实根大于-1,另一个实根小于-1,则n m ,必须满足什么关系.7. 设关于x 的方程023222=---k x kx 有两个实根都在]0,2[-之间,求k 的取值范围.8.关于x 的方程02)13(72=--+-m x m x 的两个实根21,x x 满足2021<<<x x ,求m 的范围. 9.①已知方程065)9(222=+-+-+a a x a x 的一根小于0,另一根大于2,求实数a 的取值范围.②已知方程065)9(222=+-+-+a a x a x 的存在小于2的根,求实数a 的取值范围.。
高一数学必修一函数零点试题及解析

高一数学必修一函数零点试题及解析一、选择题(每小题5分,共30分)1.函数f (x )=lg x -1x的零点所在的区间是( )A .(3,4)B .(2,3)C .(1,2)D .(0,1) 答案:B解析:∵函数f (x )=lg x -1x,∴f (2)=lg2-12=lg2-lg1012<0,f (3)=lg3-13=lg3-lg1013>0,∴f (2)f (3)<0由零点的存在性定理可知:零点所在的区间为(2,3),故选B. 2.如图是函数f (x )=x 2+ax +b 的部分图象,则函数g (x )=ln x +2x +a 的零点所在区间是( )A.⎝ ⎛⎭⎪⎫14,12 B .(1,2) C.⎝ ⎛⎭⎪⎫12,1 D .(2,3) 答案:C解析:解:由函数f (x )=x 2+ax +b 的部分图象得0<b <1,f (1)=0,从而-2<a <-1,而g (x )=ln x +2x +a 在定义域内单调递增,产品用时30 min,组装第A件产品用时15 min,那么c和A的值分别是________.答案:60,16解析:因为组装第A 件产品用时15 min ,所以cA=15 ①;所以必有4<A ,且c4=c2=30 ②,联立①②解得c =60,A =16. 8.设函数y =x3与y =⎝ ⎛⎭⎪⎫12x -2的图象的交点为(x 0,y 0),若x 0所在的区间是(n ,n +1)(n ∈Z ),则n =________.答案:1解析:画出函数y =x3和y =⎝ ⎛⎭⎪⎫12x -2的图象,如图所示.由函数图象,知1<x 0<2,所以n =1.9.若关于x 的方程|x |x -2=kx 有三个不等实数根,则实数k 的取值范围是________.答案:⎝⎛⎭⎪⎫0,12解析:由题意可知k ≠0, ∵|x |x -2=kx ,∴kx 2-2kx =|x |. 当x ≥0时,kx 2-2kx =x , 解得x =0或x =2k +1k,∴2k +1k >0,∴k >0或k <-12;当x <0时,kx 2-2kx =-x ,解:设函数f (x )=2x +x -4, ∵f (1)=-1<0,f (2)=2>0,f (x )在区间(1,2)上单调递增,∴f (x )在区间(1,2)内有唯一的零点,则方程2x +x -4=0在区间(1,2)内有唯一一个实数解. 取区间(1,2)作为起始区间,用二分法逐次计算如下:区间 中点的值 中点的函数值 区间长度 (1,2) 1.5 0.33 1 (1,1.5) 1.25 -0.37 0.5 (1.25,1.5)1.375-0.0310.25由上表可知,区间(1.25,1.5)的长度为0.25<0.3. ∴方程的实数解为1.375.能力提升12.(5分)若容器A 有m 升水,将水慢慢注入容器B ,t 分钟后A 中剩余水量y 符合指数函数y =m e -at (e 为自然对数的底).假设经过5分钟时,容器A 和容器B 水量相等,且又过n 分钟容器A 中水只有m8,则n 的值为( ) A .7 B .8 C .9 D .10 答案:D解析:⎩⎪⎨⎪⎧m ·e -5a =12m ,m ·e-a5+n=m8,温馨提示:最好仔细阅读后才下载使用,万分感谢!。
4.5.1函数的零点与方程的解同步练习-2021-2022学年高一上学期数学人教A版(2019)必修
C.2 D.3
8.f(x)= 的零点个数为()
A.3 B.2
C.1 D.0
9.已知函数f(x)=mx2+2x-1有且仅有一个正实数的零点,则实数m的取值范围是________.
关键能力综合练
一、选择题
1.下列函数没有零点的是()
A.f(x)=0B.f(x)=2
C.f(x)=x2-1 D.f(x)=x-
x
-3
-2
-1
0
1
2
3
4
f(x)
m
-4
-6
-6
-4
n
6
不求a,b,c的值,判断方程ax2+bx+c=0的两根所在的区间是()
A.(-3,-1),(2,4) B.(-3,-1),(-1,1)
C.(-1,1),(1,2)D.(-∞,-3),(4,+∞)
知识点三
判断函数零点的个数
7.函数f(x)=x3-x的零点个数是()
4.函数f(x)=lnx- 的零点所在的大致区间是()
A.(1,2) B.(2,3)
C.(3,4) D.(e,+∞)
5.函数f(x)=2x- -a的一个零点在区间(1,2)内,则实数a的取值范围是()
A.(1,3) B.(1,2)
C.(0,3) D.(0,2)
6.二次函数f(x)=ax2+bx+c的部分对应值如下表:
2.(易错题)若函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,则下列说法正确的是()
A.若f(a)·f(b)>0,则不存在实数c∈(a,b)使得f(c)=0
B.若f(a)·f(b)<0,则只存在一个实数c∈(a,b)使得f(c)=0
4.5 函数的应用(二)(精练)-2022版高中数学新同步精讲精炼(必修第一册)(教师版含解析)
4.5 函数的应用(二)【题组一 零点的求解】1.若函数()2f x x ax b =-+的两个零点是2和3,则函数()21g x bx ax =--的零点是A .1-和16 B .1和16- C .12和13 D .12-【答案】B 【解析】函数()2f x x ax b=-+的两个零点是2和3, 由函数的零点与方程根的关系知方程2=x ax b -+的两根为2和3.结合根与系数的关系得2323a b +=⎧⎨⨯=⎩,即56a b =⎧⎨=⎩, ∴()2651g x x x =--,∴g (x )的零点为1和16-,故选B.2.(2020·北京高一期中)已知函数21ln ()xf x x-=,那么方程f (x )=0的解是( ) A .1=x eB .x =1C .x =eD .x =1或x =e【答案】C【解析】依题意()21ln 0xf x x-==,所以1ln 0,ln 1,x x x e -===.故选:C 3.(2020年广东湛江)若函数()2f x x ax b =-+的两个零点是2和3,则函数()21g x bx ax =--的零点是A .1-和16 B .1和16- C .12和13 D .12-【答案】B 【解析】函数()2f x x ax b=-+的两个零点是2和3, 由函数的零点与方程根的关系知方程2=x ax b -+的两根为2和3.结合根与系数的关系得2323a b +=⎧⎨⨯=⎩,即56a b =⎧⎨=⎩, ∴()2651g x x x =--,∴g (x )的零点为1和16-,故选B.【题组二 零点区间的判断】1.(2020·浙江高一课时练习)在下列区间中,函数()43xf x e x =+-的零点所在的区间为( )A .1,04⎛⎫-⎪⎝⎭B .10,4⎛⎫ ⎪⎝⎭C .11,42⎛⎫⎪⎝⎭D .13,24⎛⎫⎪⎝⎭【答案】C【解析】因为函数()43xf x e x =+-在R 上连续单调递增,且114411221143204411431022f e e f e e ⎧⎛⎫=+⨯-=-<⎪ ⎪⎪⎝⎭⎨⎛⎫⎪=+⨯-=-> ⎪⎪⎝⎭⎩,所以函数的零点在区间11,42⎛⎫⎪⎝⎭内,故选C. 2.(2020·浙江高一课时练习)设函数3y x =与212x y -⎛⎫= ⎪⎝⎭的图象的交点为00,x y ,则0x 所在的区间是( )A .0,1B .1,2C .()2,3D .()3,4【答案】B【解析】因为根据题意可知,当x=1时,则23102x x -⎛⎫< ⎪⎝⎭-,而当x=2时,则23102x x -⎛⎫-> ⎪⎝⎭,故选B.3.(2020天津高一期中)在下列个区间中,存在着函数3()239f x x x =--的零点的区间是( ) A .(1,0)- B .(0,1)C .(1,2)D .(2,3)【答案】C 【解析】由()()1239100,2166910f f =--=-=--=.由零点存在定理知函数()3239f x x x =--在()1,2上必有零点。
高中数学 第三章 函数的应用 3.1.1 方程的根与函数的零点习题 新人教A版必修1-新人教A版高一
第三章 函数的应用 3.1.1 方程的根与函数的零点习题 新人教A 版必修1一、选择题1.下列图象表示的函数中没有零点的是导学号 22840944( )[答案] A[解析] 没有零点就是函数图象与x 轴没有交点,故选A. 2.函数f (x )=2x 2-3x +1的零点是导学号 22840945( ) A .-12,-1 B.12,1C.12,-1 D .-12,1[答案] B[解析] 方程2x 2-3x +1=0的两根分别为x 1=1,x 2=12,所以函数f (x )=2x 2-3x +1的零点是12,1.3.方程log 3x +x =3的解所在的区间为导学号 22840946( ) A .(0,2) B .(1,2) C .(2,3) D .(3,4) [答案] C[解析] 令f (x )=log 3x +x -3,则f (2)=log 32+2-3=log 323<0,f (3)=log 33+3-3=1>0,所以方程log 3x +x =3的解所在的区间为(2,3),故选C.4.函数f (x )=ln x -1x -1的零点的个数是导学号 22840947( ) A .0B .1C .2D .3[答案] C[解析] 如答图所示,易知y =ln x 与y =1x -1的图象有两个交点.5.已知曲线y =(110)x与y =x 的交点的横坐标是x 0,则x 0的取值X 围是导学号 22840948( )A .(0,12)B .(12,2)C .(12,1)D .(1,2)[答案] A[解析] 设f (x )=(110)x-x ,则f (0)=1>0,f (12)=(110)12 -12=0.1-0.25<0, f (1)=110-1<0,f (2)=(110)2-2<0,显然只有f (0)·f (12)<0,选A.6.下列函数中,在[1,2]上有零点的是导学号 22840949( ) A .f (x )=3x 2-4x +5 B .f (x )=x 3-5x -5 C .f (x )=ln x -3x +6 D .f (x )=e x+3x -6[答案] D[解析] A :3x 2-4x +5=0的判别式Δ<0,∴此方程无实数根,∴f (x )=3x 2-4x +5在[1,2]上无零点. B :由f (x )=x 3-5x -5=0得x 3=5x +5.在同一坐标系中画出y =x 3,x ∈[1,2]与y =5x +5,x ∈[1,2]的图象,如图1,两个图象没有交点.∴f (x )=0在[1,2]上无零点.C :由f (x )=0得ln x =3x -6,在同一坐标系中画出y =ln x 与y =3x -6的图象,如图2所示,由图象知两个函数图象在[1,2]内没有交点,因而方程f (x )=0在[1,2]内没有零点.D :∵f (1)=e +3×1-6=e -3<0,f (2)=e 2>0, ∴f (1)·f (2)<0. ∴f (x )在[1,2]内有零点. 二、填空题7.函数f (x )为偶函数,其图象与x 轴有四个交点,则该函数的所有零点之和为________.导学号 22840950[答案] 0[解析]∵y =f (x )为偶数,∴f (-x )=f (x ),∴四个根之和为0.8.函数f (x )=⎩⎪⎨⎪⎧2x 2-x -1,x ≤0,3x-4,x >0的零点的个数为________.导学号 22840951[答案] 2[解析] 当x ≤0时,令2x 2-x -1=0,解得x =-12(x =1舍去);当x >0时,令3x-4=0,解得x =log 34,所以函数f (x )=⎩⎪⎨⎪⎧2x 2-x -1,x ≤0,3x-4,x >0有2个零点.三、解答题9.判断下列函数是否存在零点,如果存在,请求出.导学号 22840952 (1)f (x )=-8x 2+7x +1; (2)f (x )=x 2+x +2;(3)f (x )=x 2+4x -12x -2;(4)f (x )=3x +1-7;(5)f (x )=log 5(2x -3).[解析] (1)因为f (x )=-8x 2+7x +1=-(8x +1)(x -1),令f (x )=0,解得x =-18或x =1,所以函数的零点为-18和1.(2)令x 2+x +2=0,因为Δ=12-4×1×2=-7<0,所以方程无实数根,所以f (x )=x 2+x +2不存在零点.(3)因为f (x )=x 2+4x -12x -2=x +6x -2x -2,令x +6x -2x -2=0,解得x =-6,所以函数的零点为-6.(4)令3x +1-7=0,解得x =log 373,所以函数的零点为log 373.(5)令log 5(2x -3)=0,解得x =2,所以函数的零点为2.10.已知二次函数y =(m +2)x 2-(2m +4)x +(3m +3)有两个零点,一个大于1,一个小于1,某某数m 的取值X 围.导学号 22840953[解析] 设f (x )=(m +2)x 2-(2m +4)x +(3m +3),如图,有两种情况.第一种情况,⎩⎪⎨⎪⎧m +2>0,f 1<0,解得-2<m <-12.第二种情况,⎩⎪⎨⎪⎧m +2<0,f1>0,此不等式组无解.综上,m 的取值X 围是-2<m <-12.一、选择题1.函数f(x)=ax2+bx+c,若f(1)>0,f(2)<0,则f(x)在(1,2)上零点的个数为导学号 22840954( )A.至多有一个B.有一个或两个C.有且仅有一个D.一个也没有[答案] C[解析]若a=0,则f(x)=bx+c是一次函数,由f(1)·f(2)<0得零点只有一个;若a≠0,则f(x)=ax2+bx+c为二次函数,如有两个零点,则必有f(1)·f(2)>0,与已知矛盾.2.已知函数f(x)的图象是连续不断的,有如下的x,f(x)对应值表:那么函数f(x)在区间[1,6]上的零点至少有导学号 22840955( )A.2个B.3个C.4个D.5个[答案] B3.已知f(x)是定义域为R的奇函数,且在(0,+∞)内的零点有1003个,则f(x)的零点的个数为导学号 22840956( )A.1003 B.1004C.2006 D.2007[答案] D[解析]由于奇函数图象关于原点对称且它在(0,+∞)内的零点有1003个,所以它在(-∞,0)内的零点也有1003个,又f(x)的定义域为R,所以f(0)=0.即0也是它的零点,故f(x)的零点共有2007个.4.若a<b<c,则函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)·(x-a)的两个零点分别位于区间导学号 22840957( )A.(b,c)和(c,+∞)内B.(-∞,a)和(a,b)内C.(a,b)和(b,c)内D.(-∞,a)和(c,+∞)内[答案] C[解析] 由于a <b <c ,所以f (a )=(a -b )(a -c )>0,f (b )=(b -a )(b -c )<0,f (c )=(c -b )(c -a )>0,根据零点的存在性定理可知,函数的两个零点分别位于区间(a ,b )和(b ,c )内,故选C.二、填空题5.m 的取值X 围为________时,方程x 2-(m +13)x +m 2+m =0的一根大于1,一根小于1.导学号 22840958[答案]-23<m <2 3[解析] 用数形结合的方法解题.设f (x )=x 2-(m +13)x +m 2+m ,则它的开口向上,由图象可得,方程x 2-(m +13)x +m 2+m =0的一根大于1,一根小于1的充要条件为f (1)=1-(m +13)+m 2+m =m 2-12<0.解得-23<m <2 3.6.对于实数a 和b ,定义运算“*”:a *b =⎩⎪⎨⎪⎧a ,a -b ≤1,b ,a -b >1,设函数f (x )=(x 2-2)*(x-1),x ∈R ,若方程f (x )=c 恰有两个不同的解,则实数c 的取值X 围是________.导学号 22840959[答案] (-2,-1]∪(1,2][解析] 由题意知f (x )=⎩⎪⎨⎪⎧x 2-2-1≤x ≤2,x -1x <-1或x >2.画出f (x )的图象,数形结合可得实数c 的取值X 围是(-2,-1]∪(1,2].三、解答题7.已知函数f (x )=log a (1-x )+log a (x +3)(0<a <1).导学号 22840960 (1)求函数f (x )的定义域; (2)求函数f (x )的零点.[解析] (1)要使函数有意义,则有⎩⎪⎨⎪⎧1-x >0,x +3>0,解得-3<x <1,所以函数的定义域为(-3,1).(2)函数可化为f (x )=log a [(1-x )(x +3)]=log a (-x 2-2x +3), 由f (x )=0,得-x 2-2x +3=1,即x 2+2x -2=0,x =-1± 3.∵-1±3∈(-3,1),∴f(x)的零点是-1± 3.8.已知函数f(x)=x2-2x-3,x∈[-1,4].导学号 22840961(1)画出函数y=f(x)的图象,并写出其值域;(2)当m为何值时,函数g(x)=f(x)+m在[-1,4]上有两个零点?[解析](1)依题意:f(x)=(x-1)2-4,x∈[-1,4],其图象如图所示.(2)∵函数g(x)=f(x)+m在[-1,4]上有两个零点,∴方程f(x)=-m在x∈[-1,4]上有两个相异的实数根,即函数y=f(x)与y=-m的图象有两个交点.由(1)所作图象可知,-4<-m≤0,∴0≤m<4.∴当0≤m<4时,函数y=f(x)与y=-m的图象有两个交点,故当0≤m<4时,函数g(x)=f(x)+m在[-1,4]上有两个零点.。
高一数学函数与方程试题答案及解析
高一数学函数与方程试题答案及解析1.设f(x)=3x+3x-8,用二分法求方程3x+3x-8=0在x∈(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,f(1.25)<0,则方程的根落在区间()A.(1,1.25)B.(1.25,1.5)C.(1.5,2)D.不能确定【答案】B【解析】由已知f(1)<0,f(1.5)>0,f(1.25)<0,∴f(1.25)f(1.5)<0,因此方程的根落在区间(1.25,1.5)内,故选B2.定义在R上的奇函数f(x) ()A.未必有零点B.零点的个数为偶数C.至少有一个零点D.以上都不对【答案】C【解析】∵函数f(x)是定义在R上的奇函数,∴f(0)=0,∴f(x)至少有一个零点,且f(x)零点的个数为奇数.3.函数f(x)=ax2+2ax+c(a≠0)的一个零点为1,则它的另一个零点为________.【答案】-3【解析】设方程f(x)=0的另一根为x,由根与系数的关系,得1+x=-=-2,故x=-3,即另一个零点为-3.4.若函数f(x)=3ax-2a+1在区间[-1,1]上存在一个零点,则a的取值范围是________.【答案】a≥或a≤-1【解析】因为函数f(x)=3ax-2a+1在区间[-1,1]上存在一个零点,所以有f(-1)·f(1)≤0,即(-5a+1)·(a+1)≤0,(5a-1)(a+1)≥0,所以或解得a≥或a≤-1.5.若方程x2-2ax+a=0在(0,1)恰有一个解,求a的取值范围.【答案】a<0或a>1【解析】解:设f(x)=x2-2ax+a.由题意知:f(0)·f(1)<0,即a(1-a)<0,根据两数之积小于0,那么必然一正一负.故分为两种情况.∴a<0或a>1.6.已知函数在R是奇函数,且当时,,则时,的解析式为_______________【答案】【解析】设则于是又函数在R是奇函数,所以所以当时,7.已知二次函数的最小值为3,且.求函数的解析式;(2)若偶函数(其中),那么,在区间上是否存在零点?请说明理由.【答案】(1)(2)存在零点【解析】(1)待定系数法,己知函数类型为二次函数,又知f(-1)=f(3),所以对称轴是x=1,且函数最小值f(1)=3,所设函数,且,代入f(-1)=11,可解a。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.1.1方程的根与函数的零点
练习二
一、选择题
1.函数2()41f x x x =--+的零点为( )
A 、12-+
B 、12--
C 、12
-± D 、不存在
2.函数32()32f x x x x =-+的零点个数为( )
A 、0
B 、1
C 、2
D 、3
3.三次方程3
2
210x x x +--=在下列那些连续整数之间有根( )
1)-2与-1之间 2)-1与0之间 3)0与1之间 4)1与2之间 5)2与3之间
A 、1)2)3)
B 、1)2)4)
C 、1)2)5)
D 、2)3)4)
4.若函数f(x)唯一的一个零点在区间(0,16),(0,8),(0,4),(0,2)内,那么下列命题中正确的是( )
A 、函数f(x)在区间(0,1)内有零点
B 、函数f(x)在区间(0,1)或(1,2)内有零点
C 、函数f(x)在区间(2,16)内有零点
D 、函数f(x)在区间(1,16)内无零点
5、方程5
10x x --=的一个正零点的存在区间可能是( )
A 、[0,1]
B 、[1,2]
C 、[2,3]
D 、[3,4] 6、已知[][]3
(),,,()()0,(),f x x x x m n f m f n f x m n =--∈⋅<且则在内 ( )
A 、至少有一实数根
B 、至少有一实根
C 、无实根
D 、有唯一实数根
二、填空题
7.方程42
420x x --=在区间[-1,3内至少有_____________个实数解。
8、已知y=x(x-1)(x+1)。
令f(x)=x(x-1)(x+1)+0.01则对于f(x)=0的叙述正确的序号是
___________。
1)有三个实根 2)x>1时恰有一实根 3)当0<x<1时恰有一实根 4)当-1<x<0时恰有一实根 5)当x<-1时恰有一实根。
9、已知关于x 的方程3x 2
+(m-5)x +7=0的一个根大于4,而另一个根小于4,求实数m 的
取值范围_____________。
三、解答题
10、求函数()1322+-=x x x f 零点的个数。
11、判断方程2
60x x --=的解的存在。
12、求证:方程2
5710x x --=的根一个在区间(-1,0)上,另一个在区间(1,2)上。
13、试找出一个长度为1的区间,在这个区间上函数1
()32
x f x x -=+至少有一个零点。
14、已知关于x 的方程x 2+2mx +2m +3=0的两个不等实根都在区间(0,2)内,求实数m 的取值范围.
15、国家购买某种农产品的价格为120元/担,其中征税标准为100元征8元(叫做税率为
8个百分点,即8%),计划可收购m万担。
为了减轻农民负担,决定税率降低x个百分点,预计收购量可增加2x个百分点。
f(万元)与x的函数关系式;
(1)写出税收()x
(2)要使此项税收在税率调节后达到计划的78%,试求此时的x的值。
答案: 一、选择题
1、 C ;
2、D ;
3、B ;
4、C ;
5、B ;
6、D 二、填空题
7、2
8、1)5)
9、35m <-
10
)05.1<,()01>-f ,即(-f 数在区间()1,5.1--内有零点。
同量,它在区间(0,0.5)内也有零点。
另外,0,所以1也是它的零点。
由于函数()x f 在定义域()5.1,-∞-和(1,∞+)内是增函数,所以它共有3个零点。
11、解:考察函数f(x)=2
60x x --=知图像为抛物线,容易看出
f(0)=-6<0,f(4)=6>0,f(-4)=14>0
由于函数f(x)的图像是连续曲线,因此,点B (0,-6)与点C (4,6)之间的那部分曲线必然穿过x 轴,即在区间(0,4)内必有一个点1x ,使f(1x )=0;同样在区间
(-4,0)内也有一个点2x 使f(2x )=0。
所以方程2
60x x --=有两个实数解。
12、证明:设
2()571
f x x x =--,则
f(-1)f(0)=11(1)110,(1)(2(3)5150f ⨯-=-<=-⨯=-<。
而二次函数2()571f x x x =--是连续的。
所以f(x)在(-1,0)和(1,2)上分别有零点。
即方程2
5710x x --=的根一个在(-1,0)上,另一个在(1,2)上。
13、解:1()32x f x x -=
+的定义域为22(,)(,)33-∞--+∞ 。
取区间13
[,]。
则易证:
11112()02722f -==-<+,3131
2()021322f -==>+
间13[,]22内函数f(x)至少有一个零点。
区间13
[,]22
14、解:令2()223f x x mx m =+++有图像特征可知方程f (x )=0的两根都在(0,2)
内需满足的条件是
解得35
14
-
<<-。
15、解:(1)由题设,调节税率后税率为()x -8%,预计可收购%)21(x m +万担,总金额
为120%)21(x m +万元,所以 ())%8%)(21(120x x m x f -+=。
即()()
()8040042125
32
≤<-+-
=x x x m x f 。
(2)计划税收为120%8⋅m 万元,由题设,有 ()%78%8120⋅⋅=m x f ,
即)80(088422
≤<=-+x x x ,解得2=x 。
试用函数的图象指出方程)80(088422
≤<=-+x x x 的根,即函数
())80(088422≤<=-+=x x x x g 的零点所在的大致区间。
