弹力有无及其方向的判断方法
弹力有无的判断

方法一:撤去法 撤去施力物体, 看受力物体是否 能保持原状态, 若能则说明不存 在弹力,若不能 保持原状态则说 明存在弹力。
N1
A O
N2
B
G
方法二:假设存在法 假设接触处存在弹力, 作出受力分析图,结 合物体的运动状态, 根据平衡条件或牛顿 运动定律来判断物体 间是否存在弹力。
物体受到三个力时,不可能静止,说明N2不存在, 也就是说OA对小球没有弹力。
弹力方向有无的判断
产生弹力的两个条件: 1、两物体间要直接接触 2、物体要发生弹性形变(挤压)
形变明显 肯定存在弹力
例一:小球与OA、OB都接触,且处于静止状态。小球与 各接触面之间是否都存在弹力?
A
O
B
1、若撤去接触面OA,小球不动,说 明OA对小球没有弹力
2、若撤去接触面OB,小球向下运动, 说明OB对小球有弹力
例二:静止的车厢顶部用细线竖直悬挂一小球, 小球下方与一光滑的斜面接触,小球的受力如何?
假设斜面对小球有弹力,则小球无法静止, 说明小球只受到重力和绳子的拉力。
拓展:若小球随着车厢一起向右匀加速运动,小球的受力又如何?
解析:小球向右匀加速,根据牛
v
顿第二定律可知小球的合外力向
a
右,因此斜面对小球有弹力的作
用,受力分析如图所示
练习:如图所示的情景中,两个物体a、b(a、b均 处 于静止状态,接触面光滑)间一定有弹力的
弹力有无及其方向的判定
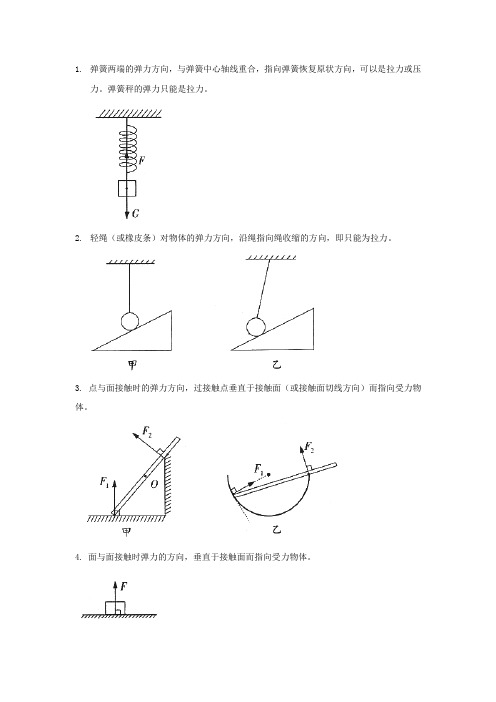
1.弹簧两端的弹力方向,与弹簧中心轴线重合,指向弹簧恢复原状方向,可以是拉力或压
力。
弹簧秤的弹力只能是拉力。
2.轻绳(或橡皮条)对物体的弹力方向,沿绳指向绳收缩的方向,即只能为拉力。
3. 点与面接触时的弹力方向,过接触点垂直于接触面(或接触面切线方向)而指向受力物体。
4. 面与面接触时弹力的方向,垂直于接触面而指向受力物体。
5. 球与面接触时弹力的方向,在接触点与球心的连线上而指向受力物体。
6. 球与球相接触时弹力的方向,垂直过接触点的分切面,通过两球球心而指向受力物体。
7. 轻杆可受拉力也可受压力作用,可沿杆也可不沿杆。
弹力的方向应视题意而定,常利用平衡条件或动力学规律来判断。
微专题8 弹力有无、方向及大小的分析方法

1.弹力有无的判断可用条件法、假设法、状态法等判断;接触面上的弹力总是垂直于“公共切面”.2.“死结”(绳子中有结点)两边的绳子拉力可以不相等.“活结”(绳子无结点且与绳子接触的滑轮、滑环等无摩擦)两边绳子是同一根绳子,拉力一定相等.(绳子是轻绳)3.有铰链的杆,弹力一定沿杆方向;没有铰链的杆,弹力可沿任意方向.4.弹力的大小一般根据平衡条件求解.1.如图1所示,小车内一根竖直方向的轻质弹簧和一条与竖直方向成α角的轻质细绳共同拴接一小球,当小车和小球相对静止,一起在水平面上运动时,下列说法正确的是()图1A.细绳一定对小球有拉力的作用B.轻弹簧一定对小球有弹力的作用C.细绳不一定对小球有拉力的作用,但是轻弹簧一定对小球有弹力D .细绳不一定对小球有拉力的作用,轻弹簧也不一定对小球有弹力2.如图2所示,两个轻环a 和b 套在位于竖直面内的一段固定圆弧上;一细线穿过两轻环,其两端各系一质量为m 的小球.在a 和b 之间的细线上悬挂一小物块.平衡时,a 、b 间的距离恰好等于圆弧的半径.不计所有摩擦.小物块的质量M 为( )图2A.m 2B.32m C .m D .2m 3.(2020·河南郑州外国语学校月考)A 、B 是天花板上的两点,一根长为l 的细绳穿过带有光滑孔的小球,两端分别系在A 、B 点,如图3甲所示;现将长度也为l 的均匀铁链悬挂于A 、B 点,如图乙所示.小球和铁链的质量相等,均处于平衡状态,A 点对轻绳和铁链的拉力分别是T 1和T 2,球的重心和铁链重心到天花板的距离分别是h 1和h 2,则( )图3A .T 1<T 2,h 1<h 2B .T 1>T 2,h 1<h 2C.T1>T2,h1>h2D.T1=T2,h1>h24.如图4,两个弹簧的质量不计,劲度系数分别为k1、k2,它们一端固定在质量为m的物体上,另一端分别固定在Q、P上,当物体平衡时上面的弹簧处于原长状态.若把固定的物体换为质量为2m的物体(弹簧的长度不变,且弹簧均在弹性限度内),当物体再次平衡时,物体比第一次平衡时的位置下降了x,重力加速度为g,则x为()图4A.mgk1+k2B.k1k2 mg(k1+k2)C.2mgk1+k2D.k1k22mg(k1+k2)5.(2019·河南洛阳市联考)城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.如图5是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是()图5A.钢索对O点的拉力变大B.硬杆对O点的弹力变小C.钢索和硬杆对O点的作用力的合力变大D.钢索和硬杆对O点的作用力的合力变小6.三个质量均为1 kg的相同木块a、b、c和两个劲度系数均为500 N/m的相同轻弹簧p、q 用轻绳连接如图6所示,其中a放在光滑水平桌面上.开始时p弹簧处于原长,木块均静止.现用水平力缓慢地向左拉p弹簧的左端,直到c木块刚好离开水平地面为止,g取10 m/s2.则该过程()图6A.q弹簧上端移动的距离为2 cm,p弹簧的左端向左移动的距离是4 cmB.q弹簧上端移动的距离为4 cm,p弹簧的左端向左移动的距离是2 cmC.q弹簧上端移动的距离为4 cm,p弹簧的左端向左移动的距离是8 cmD.q弹簧上端移动的距离为2 cm,p弹簧的左端向左移动的距离是6 cm7.(2019·贵州贵阳市模拟)如图7所示,OA、OB为竖直平面的两根固定光滑杆,OA竖直、OB与OA之间的夹角为45°,两杆上套有可以自由移动的轻质环E和F,通过不可伸长的轻绳在结点D点悬挂质量为m的物体.当物体静止时,环E与杆OA间的作用力大小为F1,环F与杆OB之间的作用力大小为F2,重力加速度为g,则()图7A.F1=mg,F2=mg B.F1=mg,F2=2mgC.F1=2mg,F2=mg D.F1=2mg,F2=2mg答案精析1.D[若小球与小车一起匀速运动,则细绳对小球无拉力;若小球与小车有向右的加速度a =g tan α,则轻弹簧对小球无弹力,故D正确.]2.C[如图所示,圆弧的圆心为O,悬挂小物块的点为c,由于ab=R,则△aOb为等边三角形,同一条细线上的拉力相等,T=mg,合力沿Oc方向,则Oc为角平分线,由几何关系知,∠acb=120°,物块处于平衡状态,故细线的拉力的合力与物块的重力大小相等,则每条细线上的拉力T=G′=Mg,所以小物块的质量为M=m,故C正确.]3.C[由于是轻绳,绳子的质量不计,则题图甲中的重力全部集中在球上,重心在球的球心,而题图乙中铁链的质量是均匀的,故其重心一定在最低点的上方,故h1>h2;对球和铁链受力分析,图甲中,A、B点对球的拉力沿着绳子的方向;图乙中,A、B点对铁链的拉力沿着该处铁链的切线方向,故题图乙中A、B两点对铁链拉力的夹角比较小,由力的合成知识知,T2较小,故C正确.]4.A [当物体的质量为m 时,设下面的弹簧的压缩量为x 1,则有mg =k 1x 1;当物体的质量为2m 时,有2mg =k 1(x 1+x )+k 2x ,联立可得x =mg k 1+k 2,A 正确.] 5.A [对O 点受力分析,共受三个力作用:钢索的拉力F A ,硬杆的弹力F B ,细线的拉力F C (设重物的质量为m ,则有F C =mg ).由硬杆始终水平可知,O 点始终静止,即处于平衡状态,根据“物体受三个共点力而处于平衡状态时,其中任意两个力的合力与第三个力等大反向”可知:钢索和硬杆对O 点的作用力的合力大小始终与细线的拉力大小相等,即保持不变,C 、D 错误;沿水平和竖直方向建立直角坐标系,设钢索与水平方向夹角为θ,则有F A cos θ=F B ,F A sin θ=F C ,且有F C =mg ,联立可得F A =mg sin θ ,F B =mg tan θ.由数学知识可知:当A 点缓慢向下移动时,θ变小,则F A 和F B 均变大,B 错误,A 正确.]6.C [开始时p 弹簧处于原长,可知q 弹簧处于压缩状态,压缩量为Δx q =mg k =10500m =2 cm ;c 木块刚好离开水平地面时,弹簧q 伸长Δx q ′=mg k=2 cm ,则q 弹簧上端移动的距离为4 cm ;p 弹簧伸长Δx p =2mg k =20500m =4 cm ,则p 弹簧的左端向左移动的距离是8 cm ,选项C 正确,A 、B 、D 错误.]7.B [套在固定光滑杆的轻质环对其作用力的方向只能是垂直于光滑杆.由此可知,当物体静止时,DE 轻绳水平,DF 轻绳与竖直方向的夹角为45°,由平行四边形定则可知,DE 轻绳中的的拉力等于mg ,DF 轻绳中的拉力等于2mg ,所以环E 与杆OA 之间的作用力大小为mg,环F与杆OB之间的作用力大小为2mg,选项B正确.]。
专题一 受力分析

专题一 受力分析一、三种力1. 重力,是由于地球对物体的吸引而使物体受到的力,只要物体在地球上,物体就会受到重力。
重力的方向:竖直向下。
2. 弹力的产生条件是接触且发生弹性形变。
判断弹力有无的方法:假设法和运动状态分析法。
弹力的方向与施力物体形变的方向相反,与施力物体恢复形变的方向相同。
弹力的方向的判断:面面接触垂直于面,点面接触垂直于面,点线接触垂直于线。
3. 摩擦力的产生条件为:(1)两物体相互接触,且接触面粗糙;(2)接触面间有挤压;(3)有相对运动或相对运动趋势。
摩擦力的方向为与接触面相切,与相对运动方向或相对运动趋势方向相反。
判断摩擦力有无和方向的方法:假设法、运动状态分析法、牛顿第三定律分析法。
如果研究的物体处在更为复杂的环境中,如周围有某种液(气)体、电场或者磁场,那么还要分析物体是否受到浮力、阻力、电场力或磁场力等的作用。
【例题1】如图所示,画出物体A 所受的弹力a 图中物体A 静止在斜面上b 图中杆A 静止在光滑的半圆形的碗中c 图中A 球光滑 O 为圆心, O '为重心。
【解析】图a 中接触处为面面接触,由于物体受重力作用,会对斜面斜向下挤压,斜面要恢复形变,应垂直斜面斜向上凸起,对物体有垂直斜面且指向物体斜向上的弹力。
图b 中B 处为点与曲面接触,发生的形变为沿半径方向向外凹,要恢复形变就得沿半径向上凸起,C 处为点与平面接触, C 处碗的形变的方向为斜向下压,要恢复形变就得沿垂直杆的方向向上,所以B 处杆受的弹力为垂直过接触点的切面沿半径指向圆心,C 处杆受的弹力为垂直杆向上。
图c 中接触处为点与曲面接触,发生的形变均为沿半径分别向下凹,要恢复形变就得沿半径方向向上凸起,所以在M 、N 两接触处对A 球的弹力为垂直过接触点的切面沿半径方向向上,作用线均过圆心O ,而不过球的重心O '。
【例题2】如图所示,判断下列几种情况下物体A 与接触面间有、无摩擦力。
图a 中物体A 静止;图b 中物体A 沿竖直面下滑,接触面粗糙;图c 中物体A 沿光滑斜面下滑;图d 中物体A 静止。
弹力有无的判断

弹力有无的判断
我们知道物体间产生弹力必须满足两个条件:一是两物体间要直接接触;二是物体要发生弹性形变(挤压)。
所以如果物体发生的是明显形变,我们可以直接根据条件就能判断出来,但是在形变不明显的情况下,我们又该如何判断呢?下面我来介绍三种方法:
一、撤去法
撤去施力物体,看受力物体是否能保持原状态,若能则说明不存在弹力,若不能保持原状态则说明存在弹力。
例一:小球与OA、OB都接触,且处于静止状态。
小球与各接触面之间是否都存在弹力?
若撤去接触面OA,小球不动,说明OA对小球没有弹力
若撤去接触面OB,小球向下运动,说明OB对小球有弹力二、假设存在法
假设接触处存在弹力,作出受力分析图,结合物体的运动状态,根据平衡条件或牛顿运动定律来判断物体间是否存在弹力。
上题中假设OA、OB对小球都有弹力,受力分析如图所示
很明显如果物体受到三个力时,不可能静止,说明N2不存在,也就是说OA对小球没有弹力。
例二:静止的车厢顶部用细线竖直悬挂一小球,小球下方与一光滑的斜面接触,小球的受力如何?
解析:假设斜面对小球有弹力,则小球无法静止,说明小球只受到重力和绳子的拉力。
拓展:若小球随着车厢一起向右匀加速运动,小球的受力又如何?
解析:小球向右匀加速,根据牛顿第二定律可知小球的合外力向右,因此斜面对小球有弹力的作用,受力分析如下图所示。
判断弹力有无及方向的方法

判断弹力有无及方向的方法作者:彭海燕来源:《职业·中旬》2012年第09期发生弹性形变的物体,由于要恢复原状,就对与它接触的物体产生力的作用,这个力就叫做弹力。
从弹力的定义中可知产生弹力的条件有二:一是两个物体直接接触;二是发生弹性形变。
任何物体都能发生形变,不能发生形变的物体是不存在的,不过有些形变比较明显,可以直接看出;但有些形变是微小的,我们肉眼不易观察,这时判断弹力的有无成了一个难点。
针对此问题,一般我们采取“假设法”。
一、假设一假设与研究对象接触的物体不存在,看物体在该位置的运动状态是否发生变化,若发生变化,则说明弹力存在;若没变化,说明弹力不存在。
例1:如图1所示,静止在光滑水平面上的均匀球体A紧贴着挡板B,这时圆球是否受到挡板的弹力作用?圆球与挡板B均匀接触,但是,挡板B是否有形变,用肉眼是无法观察出来的,因此,挡板B是否对球有弹力作用,就成了一个难点。
如果我们假设挡板B不存在,球在竖直方向的重力G和水平面对它的支持力的作用下,仍处于静止状态,所以,挡板B对球无弹力作用。
二、假设二假设与研究对象接触的物体施加了弹力(或者没施加弹力)。
根据力的作用效果分析物体的运动状态,再与实际状态相比,是否有矛盾。
若出现矛盾,则假设不正确,若两者一致,则假设正确。
例2:如图2所示,用绳子悬挂一质量为m的球,使绳子保持在竖直方向上,并使球与光滑斜面接触,小球是否受到斜面的弹力作用?如果斜面对球有弹力作用,则这个弹力的方向一定是垂直于斜面向上,使球不能处于平衡状态。
所以斜面没有弹力作用。
在前面的例1中,如果我们假设挡板B对球有弹力存在,则此时圆球在水平方向所受合力不为零,必定加速运动,与所给静止状态相互矛盾。
说明圆球与挡板B虽接触,但并不挤压,所以,挡板B对球无弹力作用。
根据弹力的定义可知,弹力的方向与弹性形变的方向相反,看起来比较容易判断,但具体应用起来,却很难。
常见支持物的弹力方向如下。
初中物理中关于弹力的判断方法

一、弹力产生的条件:弹力的产生须同时具有两个条件:1.直接接触;2.有弹性形变。
直接接触是产生弹力的前提条件,若无接触,也就无弹力可言。
发生弹性形变是产生弹力的必要条件,相互接触的物体之间并不一定能产生弹力。
例如将两个直径均为d的小球1和2,放入一个内径为2d的容器中,此时球1与球2虽然接触,但它们之间无挤压,没有发生形变,也不会产生相互作用的弹力。
二、弹力有无的判断。
对于形变较为明显的情况(如弹簧),可以根据其形变的情况对弹力有无做出直接判断;对那些形变极其微小的情况,由于形变很小,难于直接观察到,此时要判断有无弹力,通常需要采用“假设法”。
用假设法判断弹力有无的基本思路为:先假设研究对象相接触的物体没有接触,然后分析研究对象的运动状态是否发生变化,若其运动状态不变,则可断定原接触处不存在弹力;若其运动状态发生变化,则原接触处一定存在弹力。
例题 1 一个铜球放于茶杯中,铜球与杯底部和左侧壁接触,处于静止状态,若铜球与杯子的内壁都是光滑的,则侧壁对铜球有无弹力作用?解析:弹力产生的条件是:“接触且有形变”,铜球和茶杯左侧壁相接触,但是否已发生了形变,不易观察,故只能采用“假设法”。
即假设茶杯左侧壁与铜球没有接触,此时铜球受重力G与水平杯底对它的支持力作用,在这两个力的作用下,铜球仍能处于静止状态,故铜球与茶杯的左侧壁虽然相互接触,但并没有挤压发生形变,所以茶杯的左侧壁对铜球设有弹力作用。
“假设法”判断弹力有无的另一种思路为:假设所有的接触面对研究对象均存在弹力的作用,再作出假设状态下研究对象的受力分析图,判断出物体的受力情况是否与其原来题设的运动状态相矛盾。
若不发生矛盾,则假设正确;若发生矛盾,则假设不正确。
现用此思路再分析一下上述例题:假设铜球除受重力G和水平杯底支持力N外,还受到杯的左侧壁的弹力F,作出其受力分析图,由图可以看出弹力F的水平分力将使铜球产生水平向右的加速运动。
这一结果与原题设条件(铜球静止)是相矛盾的,故假设不正确,所以,球与杯左侧壁虽接触,但并不存在弹力。
弹簧弹力方向的判断

弹簧弹力方向的判断弹簧是一种常用的机械元件,它具有易于制造、可靠耐用、体积小、体重轻等优点。
由于它的特殊性,它也是机械设备中最常见的元件之一,用于安装电子设备和其他机械设备。
它的功能是提供均匀的、可预测的机械力,使系统更加稳定。
根据弹簧的功能,它的机械特性尤为重要,其中最重要的是弹簧弹力方向的判断。
弹力方向是指在机械系统中,弹簧的力在哪个方向,其力的正负性和大小。
在某个方向中,弹力的值可以从一种标准的材料中预测出来,而弹力的方向是由弹簧的结构及外部加载决定的。
弹簧弹力方向的判断主要有两种方法:一是依靠实验,模拟现实中的条件来确定其弹力方向;二是借助计算机进行数值模拟,使用数学公式来预测弹力方向。
第一种实验方法是利用测力仪实验。
首先,将将弹簧放入测力仪内,然后加载模拟实际情况下的外部力,比如加速度、重力等,以确定弹簧的真实力曲线。
测力仪在反复检测弹簧力的时候,可以得到弹簧的弹力方向的准确结果,并可以检测出弹力的最大值和最小值。
另一种判断弹力方向的方法是利用计算机来进行数学模拟。
通常,利用有限元法加以模拟,可以更加精确的得到弹簧的弹力方向。
根据外部加载的大小和方向,可以提出弹簧的数学模型,通过计算机来求解该模型,计算出弹簧的弹力方向。
无论利用何种方式来判断弹簧的弹力方向,都应该考虑到其他相关因素,比如材料的刚度,材料的温度变化等等,以确保最终的判断结果是准确的。
综上所述,弹簧的弹力方向是一个重要的机械特性。
准确判断其弹力方向有助于了解机械系统中弹簧的机械行为,对制作和改造机械设备有着重要的意义。
两种判断弹力方向的方法各有优势,综合运用可以更好地掌握弹簧的特性,实现精确控制和精细调节。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
球与面接触 沿接触点与球心连线指向受力物体
球与球接触 垂澶闷:主封封电晾的公切面指向受力物体
与弹簧中轴线重合,指向弹簧恢复的 弹簧的弹力
方向
轻绳的弹力 沿绳背离受力物体
可沿杆也可不沿杆,弹力的方向常利 杆的弹力
用平衡条件或动力学规律来判断
也 点评 通常 情况 下 弹力 的方 向都
按方法③判断,只是杆的弹力方向需要根据 方法②判断.
B.
图1
啄 解 析 A图 中 , 小 心 去 掉 斜 面 , 球 仍 静止,说明斜面与啪之间无相互作用因而
无弹 力.可以 看出,两 物体接触 但不一定 有
弹力.B图则不然,若去掉斜面小球则无法保 持在 原来的位 置静止, 这说明斜 面对小球 有 相互作用 的弹力.
1匿参
_! {},2.假设法
对于形 变不明显 的情况, 也可假设 与研 究对 象接触的 物体间有 弹力,判 断研究对 象 的运动状 态是否改变. 若运动状态改 变了, 则此处应该存在弹力,若运动状态不变,则此 处不存在弹力.
弹力一般有以下一些方法.
付
胃1.消除法
分析一 个物体对 研究对象 是否有弹 力作
用,就将该物体从想像中去掉,看研究对象能
否保持原状态,若能则说明此处弹力不存在,
若不能说明弹力存在.
状 例 1如 图 1
劢 白 所示,判断图形中静止
小球与接触斜面间是 否存在弹力 ,A中的细
线竖直,曰中的细线倾 斜.
A.
瞻 例 2如 图 2所
示,放在光滑水平面C上
的小球A是否受斜面B对
C
它的弹力作用 ?
^.
G
猎解析可假设曰
图2
对A有弹力R的作用,则小融受三个力G、
一、咒的作用,此时,球在水平方向所受的合
力不为零,必向右运动,蝴不能静止于此
处,故A不受R的作用.即B对A没有弹力作
用.也可假设将曰移去,看A是否会运动.A的
是以地球或地面上静止的物体为参考系的. 而我们学生恰恰把“相对运动”同“运动和静 止”的概念混淆一起,不能判断出滑动摩擦力 的方向.实际上,我们只要搞清楚一个问题:
“与相对运 动方向相反”是相对于 谁? 是地球
还是相对于研究对象接触的物体.
如图1所示,在匀速n—r
运转的传送带上无初速( ) 一” ( )
况,从而建立起力与运动的关系,将会在高中
阶段物理学习中迈出坚实的一步.
3 烘 例 画出图3中小球或杆受到的
弹力.除( 2) 图中的地面外,其他各接触面均 光滑 .
Q△ 盛豳
( 1)
( 2)
( 3)
( 4)
圈3
%解析根 不同接触面上弹力的特
点,作图如下:
斡F, F2磁F1童囱
( 1)
( 2)
( 3)
( 4)
图4
快 例 4如 图 5所
示,一根弹性 杆的一端固
定一个重力是2 N的小球,
引探导航·难点突破
谗加奄无及其力向的翔断方法
受力分 析是研究 物体运动 的基础, 在受 力分析时很容易出现添力、漏力的情况,从而 造成 错解.弹 力是一种 重要的作 用力,能 正 确的判断物体之间是否有弹力以及恰当地 分析出弹力的方向是高中物理学习过程中 重要的环节.
曩:一、弹力有无的判断
弹力是 指发生弹 性形变的 物体对与 之接 触的 物体产生 的作用. 弹力产生 的条件: 一 是两 物体必须 直接接触 ,二是物 体间必须 相 互挤压( 发生弹性形变) .接触是弹力产生的 前提,挤压是判断弹力有无的关键,接触的物 体间 是否有弹 性形变是 判断弹力 有无的重 要 依据 .然而除 了弹簧、 橡皮条等 发生的弹 性 形变 较为明显 外,绝大 部分的形 变都不能 直 接观 察到,因 而在弹力 有无的判 断上具有 一 定的 难度.判 断相互接 触的物体 间是否存 在
求解,求出假设的弹力风为正,则说明此处弹 §
力 向和假设 向相同,若FN为负,则说明此 §
处弹力 向和假设 向相反.
§
引探导航·难点突破
q 、叠蛾龟 ≯o t二二噬_b 何 分 析 滑 动 摩 擦 力
大小和方向
王春胜
曩’一、从概念出发。理解“运动、静止
与相对 运动" 之间 关系 通常情况下,我们所说的“运动与静止”
释放一 个物体,物体 将向
岫而
右运动.我们一般所说的777777777777777茄芳
向右运 动是以地面 为参
图1
考系的;但由于物体无初速释放在传送带上,
③几种常见模型中弹力方向的确定
弹力模型
弹力方向
面与面接触 垂直于接触面指向受力物体
ቤተ መጻሕፍቲ ባይዱ
过接触点垂直于接触面( 或接触面的 点与面接触
切面) 指向受力物体
运动状态不变,说明弹力R不存在.
,一l
曩:二、弹力方向的判断方法
①根据物体形变的方向判断
j 13j ’一一
物体所受弹力因施力物体形变产生的, :
由于物体要恢复原状,弹力的方向与形变的 三
方向相反,所以总是指向受力物体.
1
②根据物体受力情况和运动状态判断 }
物体的受力必须和物体的运动状态相符 :
合,通过对物体进行受力分析( 假设弹力的大 £ 小和方向) ,依据物体所处的运动状态列方程 盆
小球处 于静止状态时 ,弹
性杆对小球的弹力(
)
A.大小 为2N,方向 平行于斜面 向上
B.大小为1 N,方向平行于斜面向上 C.大小为2 N,方向垂直于斜面向上
D.大小为2 N。方向竖直向上 .心
髫解析弹性杆对小球的弹力与小球
受到的重力等大反向,大小为2 N,方向竖直 向上.选D.
每种性质的力都有较为显著的特点,把 握好力的特性,分析物体受力情况和运动情
