在三相电路电压电流关系
三相电路负载的三角形连接及相线电压电流关系精品资料
三相电路负载的三角形连接及相线电压电
流关系
精品资料
仅供学习与交流，如有侵权请联系网站删除谢谢2
三相电路负载的三角形连接及相/线电压电流关系
负载作三角形（△）连接的三相电路，如上图所示。
一般用于三相负载对称的情况下，如绕组为三角形接法的电动机，三角形接法的三相电路和变压器原边或副边绕组的三角形连接。
在三角形连接的三相电路中，负载的相电压UΦ等于线路上的线电压U L。
•
在三角形连接的负载对称时，三相负载中的相电流IΦ和线路中线电流I L的相量图如下右图所示。
从图中可以看出：线电流I L和相电流IΦ之间的大小关系。
同理：I v=√3 I vw、Iw=√3 I wv
即：I L=√3 IΦ
因此，在三角形连接对称负载的三相电路中，线电流（I L）等于相电流（IΦ）的√3倍（根号3≈1.73）。
线电压（U L）就等于相电压（UΦ）。
三相交流电路电压,电流的测量实验报告
三相交流电路电压,电流的测量实验报告三相交流电路电压、电流的测量实验报告一、实验目的1、熟悉三相交流电路的连接方式。
2、掌握三相交流电路中电压和电流的测量方法。
3、理解三相交流电路中电压和电流的关系。
二、实验原理三相交流电源由三个频率相同、幅值相等、相位互差 120°的正弦交流电压源组成。
在三相四线制供电系统中，有三根相线（火线）和一根中性线（零线）。
相线与相线之间的电压称为线电压，相线与中性线之间的电压称为相电压。
在星形连接（Y 形连接）中，线电压是相电压的√3 倍，且线电压超前相应的相电压 30°。
在三角形连接（△形连接）中，线电压等于相电压。
电流的测量可以使用电流表，通过将电流表串联在电路中进行测量。
三、实验设备1、三相交流电源2、交流电压表3、交流电流表4、若干导线5、三相负载（电阻、电感、电容等）四、实验步骤1、按星形连接方式连接三相负载将三相负载的三个端点分别连接到三相交流电源的三根相线上，负载的公共点连接到中性线上。
用交流电压表测量三相电源的相电压和线电压，记录测量值。
用交流电流表测量各相的电流，记录测量值。
2、按三角形连接方式连接三相负载将三相负载依次首尾相连，形成一个闭合的三角形，然后将三角形的三个顶点分别连接到三相交流电源的三根相线上。
用交流电压表测量三相电源的线电压，记录测量值。
用交流电流表测量各相的电流，记录测量值。
3、改变负载的性质（电阻、电感、电容），重复上述步骤，观察电压和电流的变化。
五、实验数据记录与处理1、星形连接｜测量项目｜测量值｜｜｜｜｜相电压 UAN ｜＿____ V ｜｜相电压 UBN ｜＿____ V ｜｜相电压 UCN ｜＿____ V ｜｜线电压 UAB ｜＿____ V ｜｜线电压 UBC ｜＿____ V ｜｜线电压 UCA ｜＿____ V ｜｜相电流 IA ｜＿____ A ｜｜相电流 IB ｜＿____ A ｜｜相电流 IC ｜＿____ A ｜2、三角形连接｜测量项目｜测量值｜｜｜｜｜线电压 UAB ｜＿____ V ｜｜线电压 UBC ｜＿____ V ｜｜线电压 UCA ｜＿____ V ｜｜相电流 IA ｜＿____ A ｜｜相电流 IB ｜＿____ A ｜｜相电流 IC ｜＿____ A ｜3、数据分析比较星形连接和三角形连接时的线电压和相电压关系，验证理论推导。
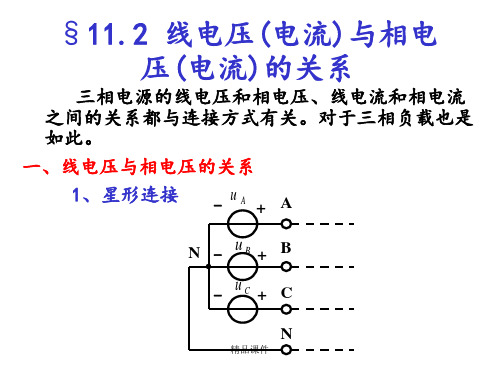
线电压(电流)与相电压(电流)的关系
N
对于对称星形电源，依次设其线电压为
•
U AB
•
•
U BC U CA
相电压为
•
U
A
•
U
B
•
UC
•
U AB
•
U
A
-
•
U
B
•••
(或UANUBNUCN)
•
U BC
•
UB
-
•
U
C
•
U CA
•
UC
-
•
U
A
精品课件
电压相量图
C
•
•
U CN
U CA
•
•
U BC
N U AN
A
•
U BN •
B
U AB
线电压与对称相电压之间的关系可以用图示电
电路应连接为 Y-△
精品课件
•
IA
•
•
•
•
I A 'B ' - I C ' A ' (12)IA'B' 3IA'B' /30
•
IB
•
IC
•
•
•
I B 'C ' - I A 'B ' (12)IB'C'
•
3IB'C' /30
•
•
•
•
I C ' A ' - I B 'C ' (12)IC'A' 3IC'A' /30
精品课件
二、线电流和相电流的关系
在三相电路电压电流关系
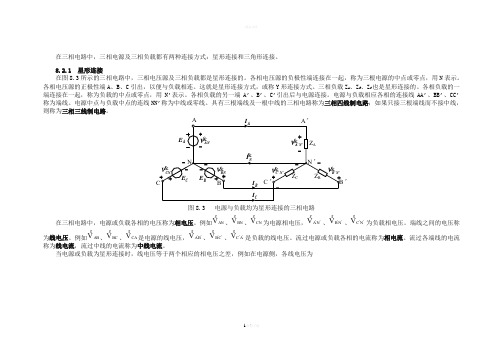
在三相电路中，三相电源及三相负载都有两种连接方式：星形连接和三角形连接。
8.2.1 星形连接在图8.3所示的三相电路中，三相电压源及三相负载都是星形连接的。
各相电压源的负极性端连接在一起，称为三根电源的中点或零点，用N 表示。
各相电压源的正极性端A 、B 、C 引出，以便与负载相连。
这就是星形连接方式，或称Y 形连接方式。
三相负载Z A 、Z B 、Z C 也是星形连接的。
各相负载的一端连接在一起，称为负载的中点或零点，用N ’表示。
各相负载的另一端A ’、B ’、C ’引出后与电源连接。
电源与负载相应各相的连接线AA ’、BB ’、CC ’称为端线。
电源中点与负载中点的连线NN ’称为中线或零线。
具有三根端线及一根中线的三相电路称为三相四线制电路；如果只接三根端线而不接中线，则称为三相三线制电路。
N-+-B I CI AE BE CE B---++-+’C ’AN V BN V图8.3 电源与负载均为星形连接的三相电路在三相电路中，电源或负载各相的电压称为相电压。
例如AN V g 、BN V g 、CN V g为电源相电压，''A N V g、''B N V g、''C N V g为负载相电压。
端线之间的电压称为线电压。
例如AB V g 、BC V g 、CA V g 是电源的线电压，''A B V g 、''B C V g 、''C A V g是负载的线电压。
流过电源或负载各相的电流称为相电流。
流过各端线的电流称为线电流，流过中线的电流称为中线电流。
当电源或负载为星形连接时，线电压等于两个相应的相电压之差，例如在电源侧，各线电压为AB AN BN BC BN CN CA CN AN V V V V V V V V Vgggg g g g g g(8.5)如果相电压是三项对称的，即2BN AN V a V gg ，2CN BN V a V gg ，2AN CN V a V gg则式(8.5)成为222303030AB AN AN AN BC BN BN BN CA CN CN CN V V a V V V V a V V V V a V Vggggo g g g g og g g go(8.6)线电压与相电压的相量图如图8.4a 或图8.4b 所示。
三相电路实验报告
三相电路实验报告摘要：本实验通过搭建三相电路并进行实验测量，验证了三相电路中电流和电压之间的关系。
实验结果表明，在三相电路中，电流之间的相位差为120度，电压之间的相位差也为120度。
此外，实验中还研究了三相电路的平衡性和不平衡性，并观察了电压和电流的波形。
引言：三相电路是现代电力系统中常见的电路配置。
三相电路中，电流和电压之间的关系是实验研究的重点，也是电力系统工程师需要掌握的基本知识。
本实验旨在通过实验测量，验证三相电路中电流和电压之间的关系，并进一步研究三相电路的平衡性和不平衡性。
实验步骤：1. 搭建三相电路，包括三个电阻、三个电感和三个电容。
2. 使用电压表和电流表分别测量三相电路中电压和电流的数值。
3. 记录实验测量数据，并绘制电流和电压的波形图。
4. 根据测量数据，计算电流和电压之间的相位差。
5. 分析实验结果，验证三相电路中电流和电压之间的关系。
实验结果与讨论：通过实验测量，我们得到了三相电路中电压和电流的测量数据。
根据这些数据，我们计算得到了电流和电压之间的相位差为120度，验证了三相电路中电流和电压之间的关系。
此外，我们还观察到了电流和电压的波形图。
在三相电路中，电流和电压的波形呈现出120度的相位差，这与我们的理论预期一致。
我们还研究了三相电路的平衡性和不平衡性。
当三相电路中的电阻、电感和电容值相等时，电路是平衡的。
在平衡电路中，三相电流和电压相等，电流之间的相位差为120度，电压之间的相位差也为120度。
而当电路不平衡时，电流和电压的相位差将会发生变化。
结论：本实验通过实验测量验证了三相电路中电流和电压之间的关系。
实验结果表明，在三相电路中，电流之间的相位差为120度，电压之间的相位差也为120度。
此外，实验中还研究了三相电路的平衡性和不平衡性，并观察了电压和电流的波形。
通过这个实验，我们对三相电路有了更深入的理解，这对我们理解电力系统中的电路配置和电力传输具有重要意义。
三相电讲解
三相电讲解三相电是一种常见的交流电供电系统。
它由三根电压相位相差120度的导线组成，分别称为A相、B相和C相。
这三相电压是在同一频率下交替变化的，通常为50Hz或60Hz。
在三相电系统中，有三个主要的电气参数需要考虑：电压、电流和功率。
这些参数的关系可以通过欧姆定律、功率定律和电流平衡原理来描述。
对于三相电系统，电压可以分为线电压和相电压。
线电压是指在两个相线之间的电压，通常用U表示。
相电压是指每根导线与中性线之间的电压，通常用V表示。
在理想情况下，线电压等于相电压的根号3倍。
电流是电荷在电路中的流动，分为线电流和相电流。
线电流是指通过导线的总电流，通常用I表示。
相电流是通过每个相线的电流，通常用Ia、Ib和Ic表示。
在理想情况下，三相电系统中的相电流相等。
功率是电的能量转换的速度，可以分为有功功率和无功功率。
有功功率是实际做功的功率，通常用P表示。
无功功率是在电路中储存和释放的能量，通常用Q表示。
在理想情况下，三相电系统中有功功率等于线电压、相电压和相电流的乘积。
三相电系统的特点之一是其高效率和功率密度。
由于线电压等于相电压的根号3倍，所以在相同功率条件下，三相电系统可以比单相电系统更有效地传输电力。
此外，三相电系统还具有相电压平衡和相电流平衡的特点。
相电压平衡是指三相电压相差120度，相电流平衡是指三相电流相等。
这些特点可以使三相电系统更加稳定和可靠。
总的来说，三相电系统是一种常见而重要的电力供应系统，广泛应用于各种工业和商业领域。
对于理解和应用三相电系统，了解电压、电流和功率的关系以及其特点是至关重要的。
三相电机功率计算公式
三相电机功率计算公式P = √3 * U * I * cos(θ)其中，P代表三相电机的功率，√3是3的平方根，U代表电机的相电压，I代表电机的相电流，cos(θ)代表功率因数。
1.功率公式：P = U * I * cos(θ)根据功率公式，功率等于电压乘以电流再乘以功率因数。
2.对称三相电路的电压和电流关系：假设三相电路的电压和电流的关系如下：Ua = U * cos(ωt + α)Ub = U * cos(ωt + α - 120°)Uc = U * cos(ωt + α - 240°)Ia = I * cos(ωt + β)Ib = I * cos(ωt + β - 120°)Ic = I * cos(ωt + β - 240°)其中，Ua、Ub、Uc分别代表三相电压的幅值，Ia、Ib、Ic分别代表三相电流的幅值，ω代表角频率，t代表时间，α代表电压相角，β代表电流相角。
3.三相电机功率计算公式推导：根据对称三相电路的电压和电流关系，我们可以得出各个相的功率表达式：Pa = Ua * Ia * cos(ωt + α) = U * cos(ωt + α) * I *cos(ωt + β) * cos(ωt + α)Pb = Ub * Ib * cos(ωt + α - 120°) = U * cos(ωt + α - 120°) * I * cos(ωt + β - 120°) * cos(ωt + α - 120°) Pc = Uc * Ic * cos(ωt + α - 240°) = U * cos(ωt + α - 240°) * I * cos(ωt + β - 240°) * cos(ωt + α - 240°)在三相电路中，电压和电流的相角相差120°，因此三个相的功率之和为0，即Pa+Pb+Pc=0。
三相用电电流计算公式
三相用电电流计算公式
在三相电路中，为了计算电流的大小以及选择适当的电线和保护设备，有一些公式可以使用。
以下是三相用电电流计算公式：
1. 直流电流转换为三相相电流：
在三相电路中，直流电流可以转换为相电流（I_phase）的公式如下：
I_phase = I_dc / (√3 * V_line)，其中I_dc是直流电流的值，V_line是线电压的值。
这个公式适用于将直流电流转换为每相的相电流的场景。
2. 三相电流之间的关系：
在三相电路中，相电流和线电流之间有一定的关系。
相电流（I_phase）和线电流（I_line）之间的关系可以通过以下公式计算：
I_line = √3 * I_phase。
换句话说，相电流的值乘以√3就是线电流的值。
3. 三相功率的计算：
三相功率（P_phase）可以通过以下公式计算：
P_phase = √3 * V_line * I_phase * power factor。
其中V_line是线电压的值，I_phase是相电流的值，功率因数（power factor）是电路的功率因数。
以上是三相用电电流计算公式的简要描述。
使用这些公式，可以更好地理解和计算三相电路中的电流，以便正确选择线路和保护设备，并确保系统的稳定和安全运行。
三相电路相电压和相电流的相位差
三相电路相电压和相电流的相位差
在一个三相交流电路中，相电压和相电流之间的相位差取决于电路的类型和连接方式。
在正常的三相交流电路中，相电压和相电流的相位差通常是120度。
具体来说，在三相交流电路中，有三个相电压分别被标记为Ua、Ub 和Uc，以及三个相电流分别标记为Ia、Ib和Ic。
相电压和相电流的波形通常是正弦波。
在正常情况下，Ua、Ub和Uc之间的相位差是120度，即每个相电压相对于其他两个相电压相差120度。
同样，Ia、Ib和Ic之间的相位差也是120度，即每个相电流相对于其他两个相电流相差120度。
这种相位差的存在是由于三相电源之间的电气角度差，它们的波形形状和频率相同，但是在时间上存在一定的延迟。
这种120度的相位差是三相电路正常运行的基本特征，它在电力传输、工业生产和其他领域都有广泛的应用。
正是这种相位差，使得三相交流电路能够高效地传输和分配电能。
三相电路线电压电流和相电压电流的关系
I C U BC
C
Y接三相电源
电压关系：
设 U•AU0o U C1120
U•BU120o U A1120
U •CU 12o 0U B1120
UC •
•
•
U AB U A U B
• 120•
•
1U2B0C °U B
UC
•
U
A
°U• C
中性点 +
•
•
UA
– X
Y
Z
•
C UC
•
UB
•
B IB
•
IC
•
•
U A B U CA
N
B
•
U BC
Y – UB
•
Z – UC
+
+
B C
C
N
线电流：
•
IA
，
•
IB
，
•
IC
线电压：U • A
B ， U • BC
，
•
U
CA
相电压：U • A ，
•
U
B
，
•
UC
8
2）三角形()联接
•
IA
ZA
A
+
A
– +
–
第十二章 三相电路
§12-1 三相电路 §12-2 线电压（电流）和相电压
（电流）的关系 §12-3 对称三相电路的计算 §12-4 不对称三相电路的概念 §12-5 三相电路的功率
1
§12-1 三相电路
三相电路由三相电源、三相负载和三相输电线路 三部分组成。
三相电路的优点
三相交流电路电压、电流的测量
五、数据处理表1验证对称三相电路的√3关系：电压：表1-1总结三相四线制供电系统中中线的作用。
由表1，当为三相四线制供电系统时，对于平衡负载电流一般较小，若达到真正的平衡则中线电流应为0。
对于不平衡负载，中线电流一般比较大，可能大于线电流、相电流。
因此，对于平衡负载可不需要中线；对于不平衡负载，一定需要中线，若无中线，则会导致有的相电流过低而无法正常工作，有的相过高而损坏用电器。
因此，三相四线制供电中中线的作用是流过三相负载的不平衡电流，来保持中性点的零点位。
表2电流：表2-2由表2-2知，电流关系符合的还好，只是第一组数据由于不平衡负载的原因而出现了较大的偏差。
不对称三角形连接的负载，能否正常工作？实验能否证明这一点？对于只一点是可以肯定的，它能正常工作，因为我看到了对应的灯都亮了。
我们可以计算通过各灯泡的电流，计算表明，通过每一个灯泡的电流大概为70mA ，阻抗模大概为3082Ω。
这足够使那些灯泡亮了，于是，实验说明了这一点。
不对称负载三角形连接的相量图如下。
验证实验数据的正确性。
所用的阻抗是灯泡，其相当于电阻。
故未改变相位，于是各相电流相差120°。
I AB =69.08∠0°mA , I BC =145.7∠120°mA , I CA =212.9∠−120°mA 则I AB′=I BC +I CA =195.7∠196.8° I 0=I AB +I AB ′=268.27∠192.5°U AB =219.5∠0°V , U BC =221.4∠120°V , U CA =215∠−120°VI 0I AB′I CAI BCI AB。
三相电路 线电压电流和相电压电流的关系
A'
•
IB
B'
•
IC
C'
•
I AB
ZAB
线电压： ZCA
•
I 相电压： C A
•
ZBC
I B C
线电流： 相电流：
三角形联接
当ZABZBCZCA 时称， 为对称三相负载
U A'B' ,U B'C' ,U C'A'
U A'B' ,U B'C' ,U C'A'
IA, IB , IC
I ， I ， I • A B
三相电源通常由三相同步发电机产生三相绕组在空间互差120当转子以均匀角速度转动时在三相绕组中产生感应电压形成三个频率相同振幅相等初相位依次相差120的正弦电压源称为对称三相电源
三相电路 线电压电流和相电压 电流的关系
§12-1 三相电路 三相电路由三相电源、三相负载和三相输电线路三部分组成。
三相电路的优点
1）
Il 3I p
2）线电流滞后相电流30°。
3）若相电流对称，则线电流也对称。
21
下次课内容： • 12.3 对称三相电路的计算 • 12.4 不对称三相电路的概念
• 12.5 三相电路的功率
22
谢谢！
20
IA IA B IC A IABIAB1 12 0 IB IBC IA B IBC IBC1120 IC IC A IBC ICA ICA1120
IC A
120°
IB C
120°
IAB
120°
IA IB IC
3IAB 30 3IBC 30 3ICA 30
三相电路的电压和电流
B
y
C
z
N N
图5.10.1负载星形连接电路
在三相电路中，如图5.10.1所示，当负载为星形 连接时，相电流等于线电流。在三相四线制时，中 线电流等于三个相电流的相量和。即：
IN IA IB IC
当电源和负载对称时，中线电流为零，当负载
不对称时，中线电流不等于零。线电压与相电压的
关系为：
不为零。
3. 三相电源的相序测定
C
A
x
B
y
z C
图 5.10.2相序器电路
三相电源的相序测定可根据中点位移的原理， 用实验方法来测定。测定相序的实验电路如图5.10.2 所示，采用三线制不对称星形连接，假定任意一一 相为A（U）相，其余两相为负载大小同的白炽灯， 选择适当电容器C的值，使两相的白炽灯的亮度有 明显的差别。根据理论分析，灯较亮的一相相位超 前于灯较暗的一相，而滞后于接电容的一相。因 此，灯较亮的一相为B（V）相,灯较暗的一相为C（ W）相。
2. 三相四线制，负载为星形连接。 按图5.10.1接线，测量线电压、相电压、中心点
位移电压、线电流、相电流、中线电流。注意：没
有特殊说明的负载均为两只串联的40W白炽灯（以
下类同）。
表5.10.1 三相四线制星形连接 电压单位：V 电流单位：A
三相负载情况 UAB UBC UCA UA UB UC UNN' IA
实验目的
1. 加深理解三相电路中线电压与相电压、线电流 与相电流之间的关系。
2. 掌握三相电路的正确连接方法及测量方法。 3. 研究三相不对称负载为星形时，中心点的位移
和其所起的作用。
实验原理
1. 三相电路 三相电路是由三相电源供电的电路。三相电源能
三相电路、线电压(电流)与相电压(电流)的关系
A
•
UA
Y UA
-
•
UC
–
B
N
•
UB
•
UB
B
Z– •
C
UC
C
N
X、 Y、 Z 接在一起的点称为Y形联结对称三 相电源的中性点，用N表示。
返回 上页 下页
（2）三角形联结(形联结)
Z
A
AZ
+ •
•
UC
•
UA
–
UA
– +
–
CY – • UB
+
X
B
•
U
C
X
+
•
UB
C
Y
B C
注意
三角形联结的对称三相电源没有中性点。
X
YZ
X、Y、Z 三端称为末端。
②波形图
u uA uB uC
O
t
返回 上页 下页
③相量表示
•
UA U
0
•
UB U
120
•
UC U
120
④对称三相电源的特点
U C
120°
•
120°
UA
120°
U B
UA UB
uA uB uC 0
•
•
•
UA UB UC 0
返回 上页 下页
⑤对称三相电源的相序
L
P
(3) 线电压相位领先对应相电压30o。
所谓的“对应”：对应相电压用线电压的 第一个下标字母标出。
•
•
UAB U AN
•
•
UBC U BN
•
•
UCA U CN
三相电压电流的关系
三相电压电流的关系可以用基尔霍夫定律来描述，它是一个基本的电路定律，用于描述电路中各支路之间的电流和电压关系。
对于三相交流电路，基尔霍夫定律可以表述为：
1. 在任一时刻，流入任一节点的电流之和等于流出该节点的电流之和。
2. 在任一时刻，沿任一闭合回路的电压降之和等于该闭合回路中各段电压升之和。
根据基尔霍夫定律，可以得到三相电压电流之间的关系：
1. 三相电流之和为零。
2. 三相电压之和为零。
3. 三相功率之和为零。
这些关系可以用于三相交流电路的分析和计算，例如，计算三相电路的功率、电压和电流等参数。
三相电路线电压,相电压,线电流和相电流的关系
三相电路线电压,相电压,线电流和相电流的关系1. 引言1.1 概述三相电路是电力系统中常见的一种电路形式，它由三个互相位移120度的正弦交流电压或电流组成。
在实际应用中，我们经常会涉及到三相电路中的线电压、相电压、线电流和相电流这些参数。
理解和掌握这些参数之间的关系对于正确分析和设计电力系统至关重要。
1.2 文章结构本文将围绕三相电路中的线电压、相电压、线电流和相电流这几个概念展开讨论。
首先介绍三相电路的基本概念，包括其简介、线电压和相电压的定义以及二者之间的关系。
接着我们将介绍线电流和相电流的定义以及其与线/相电压之间的关联性分析。
最后，我们将引入四参数模型，并详细介绍计算线/相量之间关系的具体方法。
1.3 目的本文旨在帮助读者深入了解并掌握三相电路中线/相量之间关系的基础知识。
通过对线/相量概念及其关联性进行详细解析，读者可以更好地理解和利用这些参数进行电力系统的分析和设计。
同时，本文还旨在引入四参数模型，为读者提供更为准确和灵活的线/相量计算方法。
2. 三相电路线电压和相电压的概念2.1 三相电路简介在电力系统中，三相电路是最常见的一种形式。
它由三个相位不同的交流电源组成，每个交流电源间隔120度。
这种配置能够提供比单相电路更高效和稳定的功率传输。
2.2 线电压和相电压定义在三相系统中，有两种类型的电压：线电压和相电压。
线电压（或称为外部观测到的总体电压）是指任意两个相邻支路之间的差值。
也就是说，在一个三相系统中，我们可以通过测量任意两个相邻支路之间的差值来得到线电压。
而相电压是指各个支路与共联点（星型连接中的中性点或者三角形连接中的接地点）之间的差值。
换句话说，它是通过测量各个支路与共联点之间的差值来获得。
2.3 线电压和相电压之间的关系在理想情况下，线电压和相电压之间具有简单且直接的关系。
对于Δ型连接，即三角形连接方式，线电压等于根号3乘以相电压。
而对于Y型连接，即星型连接方式，线电压等于相电压。
三相电路电压,电流的测量,实验报告
三相电路电压,电流的测量,实验报告三相交流电路电压、电流的分析与测量(含数据处理)三相交流电路电压、电流的分析与测量一、实验目的1(掌握三相负载作星形联接、三角形联接的方法，验证这两种接法时线、相电压及线、相电流之间的关系。
二、原理说明1接)，当三相对称负载作Y线电流Il 等于相电流Ip，即Ulp Il,IpI0,0，所以可以 ,必须采用三相四线制接法，即Y0倘若中线断开，会导致三相负载电压的不对称，致使负载轻的那一相的相电压过高，使负载遭受损坏;负载重的一相相电压又过低，使负载不能正常工作。
尤其是对于三相照明负载，无条件地一律采用Y0 接法。
3(当不对称负载作?接时，Il，但只要电源的线电压Ul 对称，加在三相负载上的电压仍是对称的，对各相负载工作没有影响。
三、实验设备及器件调压器的输出，使输出的三相线电压为220V，按表6-3-3-1数据表格所列各项要求分别测量三相负载的线电压、相电压、线电流(相电流)、中线电流、电源与负载中点的电压，记录之。
并观察各相灯组亮暗的变化程度，特别要注意观察中线的作用。
图6-3-3-1 路2按图6-3-3-2调节调压器，使其输出线电压为6-3-3-2数据表格要求进行测试图6-3-3-2 三相负载三角形联接的实验线路五、实验报告1(三相负载根据什么条件作星形或三角形连接,答:一般电机功率大于11kw就采(来自: 写论文网:三相电路电压,电流的测量,实验报告)用星,三角启动，否则采用三角形直接启动，一般不采用星形接法。
2(试分析三相星形联接不对称负载在无中线情况下，当某相负载开路或短路时会出现什么情况,如果接上中线，情况又如何,6( 实验是否能证明这一点,Vl响7 并求出线电表6-3-3-1三相负载星形联接实验数据表篇二:三相电路实验报告实验一一、实验名称三相电路不同连接方法的测量二、实验目的:1. 理解三相电路中线电压与相电压、线电流与相电流之间的关系。
2. 掌握三相电路的正确连接方法与测量方法。
三相电路的电压和电流
三相电路的电压和电流
三相电路是指至少存在三个独立的相位的直流或交流电路。
用极坐标定义三个相电路
的电压时，它们分别抵消了各自的有效值并且是相位相差120度的情况。
三相电路对建筑
物供电是非常重要的，用于支持大部分的照明设备，可以将数据传输到不同的地方。
此外，三相电路的电压和电流也被广泛用于一些工业应用，例如电梯，HO灯，洗衣机等。
三相电路的电压和电流有三种不同的类型：单相电压，交流和直流。
在单相电压中，
每个相位的电压是相同的，而且不相互作用。
在交流电路中，每个相位的电压都会交替出现，而且相位之间相差120度。
最后，在直流电路中，每个相位的电压都是恒定的。
三相电路的电压大小取决于其负载的情况，通常来说，它们的电压范围为200V~600V
之间。
而且每个相位的电压相位相差120度，三相电流对系统来说也是非常重要的，因此
三相电流的有效值必须要通过测量来得到准确的值，才能确保电压的稳定性。
三相电路中的电压电流关系
负载对称
负载不对称
三、实验任务与方法
1、测试三相电源的相序
三、实验任务与方法
2、按照表5-1要求测量各种情况下三相电路中的电压和电流。 表 5-1
UA´B´ UB´C´ UC´A´ UA´N´ UB´N´ UC´N´ UN´N IA IB IC IN´N
负 载 对 称
有中线
无中线
A相 开 路
有中线
制三相电路的特点。 2. 回答思考题1。
亮B A 暗C
图1 图2
UBN´> UCN´ 据此，对相序未明确的三相电源，可采取在其中任意一 相接一电容，并将该相设定为A相，在其它两相分别接 入规格相同的白炽灯，如图2所示。开启电源后，灯比 较亮的一相就是B相。
二、实验原理 3、Y-Y电路特点 ⑴电路结构
三相四线制 (Y0-Y0)
. UC .+ UA A N ZN ZC C ZA
无中线
C相 短 路
无中线
扩展内容
Y-△对称三相电路的电压、电流关系。 （测量线电流以及负载端的相电压、相电流，自拟数据表格）
+ +
UA UB UC
-
A
B
C
IA
Z
IB I BC
Z
I AB
Z
N
+
-
IC
测试原理图
I CA
须经指导老师同意后方可合上电源！
精品课件！
精品课件！
四、实验报告要求
1. 由实验结果说明三相三线制三相电路和三相四线
A
N
+
C
-
-.
UB + B
ZB B
三相三线制 (Y-Y)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
在三相电路中，三相电源及三相负载都有两种连接方式：星形连接和三角形连接。
8.2.1 星形连接
在图8.3所示的三相电路中，三相电压源及三相负载都是星形连接的。
各相电压源的负极性端连接在一起，称为三根电源的中点或零点，用N 表示。
各相电压源的正极性端A 、B 、C 引出，以便与负载相连。
这就是星形连接方式，或称Y 形连接方式。
三相负载Z A 、Z B 、Z C 也是星形连接的。
各相负载的一端连接在一起，称为负载的中点或零点，用N ’表示。
各相负载的另一端A ’、B ’、C ’引出后与电源连接。
电源与负载相应各相的连接线AA ’、BB ’、CC ’称为端线。
电源中点与负载中点的连线NN ’称为中线或零线。
具有三根端线及一根中线的三相电路称为三相四线制电路；如果只接三根端线而不接中线，则称为三相三线制电路。
N -+-A
I B I C
I A
E B
E C
E B
-
--+
+
-+’
C ’
AN V BN V 'C
图8.3 电源与负载均为星形连接的三相电路
在三相电路中，电源或负载各相的电压称为相电压。
例如AN V 、BN V 、CN V 为电源相电压，''A N V 、''B N V 、''C N V 为负载相电压。
端线之间的电压称为线电压。
例如AB V 、BC V 、CA V 是电源的线电压，''A B V 、''B C V 、''C A V 是负载的线电压。
流过电源或负载各相的电流称为相电流。
流过各端线的电流称为线电流，流过中线的电流称为中线电流。
当电源或负载为星形连接时，线电压等于两个相应的相电压之差，例如在电源侧，各线电压为
AB AN BN BC BN CN CA CN AN V V V V V V V V V ⎫
=-⎪
⎪
=-⎬
⎪
=-⎪
⎭ (8.5)
如果相电压是三项对称的，即2
BN AN V a V =，2
CN BN V a V =，2
AN CN V a V =则式(8.5)成为
222
330330330AB AN AN AN BC BN BN BN CA CN CN CN V
V a V V V V a V V
V V a V V ⎫
=-=∠⎪
⎪
=-=∠⎬
⎪
=-=∠⎪
⎭ (8.6)
线电压与相电压的相量图如图8.4a 或图8.4b 所示。
由于在复平面上相量可以平移，所以这两种表示方法是一致的。
由式(8.6)及相量图可见，如果相电倍，也就是
lm pm
V = (8.7)
式中V lm 和V pm 分别表示线电压及相电压的振幅。
在相位关系上，AB V 、BC V 、CA V 的相位分别超前于AN V 、BN V 、CN V 相位30︒。
以上分析对于星形连接的负载也是适用的，因此不再另行讨论。
对于星形连接的电源或负载，线电流等于相应的相电流，例如电流A I 、B I 、C I 既是相电流又是线电流。
BN
V CN
V BC
V AB V CA
V AN
AB
V CA
V AN
V CN V AN V -BN
V -CN
V -BN
V
(a) (b)
图8.4 星形连接三相电源线电压和相电压的相量图
8.2.2 三角形连接
在图8.5所示的三相电路中，对称三相电压源是依次相连的，相位超前的电压源的负极性端与相位滞后的电压源的正极性端相连，也就是Z 与A 、X 与B 、Y 与C 分别连接。
三相电压源形成回路，然后从三个连接点引出端线，这就是三角形连接方式，也可称为△连接方式。
+
+
’
B
'A I B I C
I A
E B
E C
E Y
X
图8.5 电源及负载均为三角形连接的三相电路
此电路中三相负载也是三角形连接的。
因为三角形连接方式没有中点，电源与负载之间只有三根端线相连接，不可能有中线，所以是三相三线制电路。
当采用三角形连接方式时，线电流等于两个相应的相电流之差。
例如在负载侧，线电流
''''''''''''A A B C A B B C A B C C A B C I I I I I I I I I ⎫
=-⎪
⎪
=-⎬
⎪
=-⎪
⎭ (8.8)
如果相电流是三相对称的，即''''C A A B I a I =，''''A B B C I a I =，''''B C C A I a I =，则
''''''''''''(1)330(1)330(1)330A A B A B B B C B C C C A C
A I a I I I a I I
I a I I ⎫
=-=∠-⎪
⎪
=-=∠-⎬
⎪
=-=∠-⎪
⎭ (8.9)
线电流与相电流的相量图如图8.6a 或图8.6b 所示。
此时线电流也是三相对称的。
线电流的振幅I lm 是I pm
lm pm
I (8.10)
线电流A I 、B I 、C I 的相位分别滞后于相电流AB I 、BC I 、CA I 的相位30︒。
对于三角形连接的电源，线电流与相电流的关系与上述分析结果类似，读者可自行分析。
C
I ''
A B I ''
B C I ''
C A I B I A
I ''
C A I -''
A B I -''
B C I -A
I B
I I ''
C A I ''
A B I ''
B C I
(a) (b)
图8.6 三角形连接负载的线电流和相电流的相量图
对于采用三角形连接方式的三相电源或三相负载，线电压等于相应的相电压。
例如在电 源侧，线电压AB V 、BC V 、CA V 也是电压源的相电压。
应该指出，如果将对称三相电压源按三角形方式连接时，必须按图8.5所示的正确方法连接。
这样，由三相电压源组成的回路中，电动势之和
0A B C E E E ++=。
在不接负载时回路中的电流等于零，即电源内部不会有环行电流。
如果连接方式不正确，例如误将A E 反接（见图8.7a ）,则回路中
电动势之和
2A B C A E E E E -++=-
相应的相量图如图8.7b 所示。
由于电源内部的阻抗（图中未标出）是很小的，所以在电动势作用下，电源内部将产生很大的环行电流，会使电源（例如发电机）损坏，这是必须避免的。
上面讨论了电源与负载均作星形连接(简称星形-星形连接)及电源与负载均作三角形连接(简称三角形-三角形连接)的两种三相电路。
还可以有电源作星形连接、负载作三角形连接(简称星形-三角形连接)的三相电路及电源作三角形连接、负载作星形连接(简称三角形-星形连接)的三相电路。
这两种电路是三相三线制的。
星形连接的线电压与相电压之间的关系及线电流与相电流之间的关系可以分别进行分析。
上面分析所得的结论仍适用。
+
+
+
C
E B
E A
E B
E C
E A B C
E E E -++A
E -
(a) (b) 图8.7 接法有误的三角形连接三相电源。