电磁场的边界条件与电磁波的辐射和传播
电磁场-电磁波的衍射和散射

边缘绕射射线场 射线入射在物体的边缘时会发生边缘绕射。 一条入射线将激励起无穷多条绕射线,绕射线都位于一个圆锥面上,称为凯勒圆 锥。
凯勒圆锥
绕射线
关于凯勒圆锥的概述 圆锥面顶点在绕射点
绕射点 入射线
圆锥轴为绕射点所在边缘或边缘的切线
电磁场-电磁波的衍射和散射
1 电磁波的衍射
1.1 衍射问题
电磁波在传播过程中遇到障碍物或者透过小孔时,其传播方向会发生改变,这种 现象称为电磁波的衍射。
口面天线和缝隙天线的辐射属于衍射问题。 光学中分析光的衍射利用惠更斯原理。电磁波衍射的研究则利用基尔霍夫公式- 惠更斯原理的数学公式。
1.2 基尔霍夫公式
其中,en为垂直于表面S指向体积内的单位矢量。 用格林函数表示单位正点源产生的标量场,且无限大自由空间中有
G r , r e jkR
4 R
式中R为源点到场点的距离,且格林函数G满足波动方程:
2Gr,r k2Gr,r r r
将格林公式中的用格林函数G替换,并将积分变为对源点坐标积分,同时考虑格林
en dS
如果屏右边的观察点很远,即考虑远场衍射(夫琅和费衍射),上式可以简化为以
下形式:
r e jkr
4 r
e jk
S0
r
en
r
jk
en
r dS
理想导体屏上的小孔衍射
设理导体屏上有一个小孔,一个平行极化的平面波以θ1为入射角入射,如图。假 设平面波为
r 0e jk1 r , 其中0为原点处的 值。
几何绕射理论概念 几何绕射理论(OTD)由凯勒于1951年在几何光学的基础上提出,其基本概念为:
电磁场与电磁波第六章

1 H R 0 H R 0 1 cos 1 2 cos 2 1 H I 0 H I 0 1 cos 1 2 cos 2
(6-1-23)
T//
2 H T0 1 H I 0
2 2 cos 1 1 cos 1 2 cos 2
(6-1-1)
其中
k1 1 1 , k 2 2 2
入射波、反射波、折射波的电场矢量分别为
E I E I 0e j kI r , E R E R0e j kR r , ET ET 0 e j kT r
(6-1-2)
介质 1 中的总电场是入射波与反射波的叠加,即 E1= EI+ ER; 介质 2 中的仅为折射波,E2= ET 。 下面,根据电磁场的边界条件,由入射波的 kI和 EI0、HI0 来确定反射波和折射波的 kR、kT 以及 ER0、HR0、ET0、HT0。
第六章 平面电磁波的反射与折射
6.1.1 反射、折射定律
首先来确定反射波和折射波的波矢量方向。 由交界面 z = 0 处两侧的切向分量连续的边界条件和式
(6-1-2),可得
j (k Ix x k Ix y ) j ( k Rx x k Ry y ) j ( k Tx x k Ty y )
只考虑 E 和 H 的切向分量边界条件即可。
6.1 电磁波的反射、折射规律
设介质 1 和介质 2 的交界面
为无穷大平面,界面法向沿 z 方 向,平面电磁波以入射角I 由介 质 1 射向介质 2,如图所示。
第六章 平面电磁波的反射与折射
入射波、反射波、折射波的波矢量分别为
k I ekI k1 , k R ekR k1 , kT ekT k 2
电磁场与电磁波矢量分析

03
电磁场与电磁波的矢量 分析
麦克斯韦方程组
描述电磁场的基本规律,包括电场和 磁场的变化关系。
揭示了电磁场之间的相互依存和制约 关系,是电磁波传播和辐射的基础。
由四个基本方程组成,包括高斯定律、 高斯磁定律、法拉第定律和安培定律。
波动方程与亥姆霍兹方程
01
波动方程描述了电磁波在空间中传播的规律,是麦克斯韦方程 的简化形式。
电磁场与电磁波的特性
01
02
03
波动性
电磁波以波动的形式传播, 具有振幅、频率和相位等 波动特性。
横波
电磁波的电场和磁场振动 方向与波的传播方向垂直, 是一种横波。
传播速度
电磁波在真空中的传播速 度为光速,在其他介质中 的传播速度受介质影响。
电磁场与电磁波的应用
通信
探测
加热
科学研究
无线电波、微波等电磁 波广泛应用于通信领域, 实现信息的传输和接收。
总结词
磁偶极子是由两个电流环组成的系统,其产生的电磁波磁场 分量占主导地位,具有与电偶极子不同的辐射特性。
详细描述
磁偶极子由两个平行的环形电流组成,当其受到激发时,将 产生电磁波向外传播。磁偶极子的辐射场在远场近似下遵循 朗道辐射模式,其磁场分量占主导地位,且具有与电偶极子 不同的方向性和强度分布。
不均匀介质中的传播
折射与反射
当电磁波遇到不同介质的分界面时,会发生折射和反射现象。折 射和反射的角度、强度等特性与介质的性质有关。
散射与吸收
在不均匀介质中,电磁波的传播路径会发生散射,能量会因为介质 的吸收而逐渐减小。
多层介质传播
当电磁波在多层介质中传播时,需要考虑到不同介质分界面上的折 射、反射、散射和吸收等复杂现象。
电磁波的传播

E E
1 i 20 1 i 20
1/ 2 1/ 2
▪ 反射系数-沿法线方向的反射能流与入射能流之比:
R
@ E E
2
1 20 1 20
1/2 2
1/2 2
1 1 2
1
20 1
良导体是良反射体
小结
➢导体内的自由电荷分布:良导体内部没有自由电荷分布, 电荷只能分布于导体表面上
➢导体内的电磁波:(复电容率) 描述导体与绝缘介质的 两组方程形式相同 E 导体
E v H
0 0
导体中电磁场方程形式与绝缘介质完全一样
导体可以视为具有复介电常数的介质 10
导体复电容率物理意义
v
vv v
H i E E i E
传导电流 位移电流
位移电流与电场有90相位差,不消耗功率.传导电 流与电场同相,耗散功率密度12Re(J*E).
i
体表面上电磁波的反射和折射问题.
▪ 只讨论垂直入射情形,电磁场边界条件:
E E E H H H
Bv
evk
v E
v H
i
e4
nv
v E
H H
0 0
0 1/2 E 0 1/2 E
H
0 1/2 ei /4E
真空或绝缘介质中
良导体中
良导体也是良反射体
E E E
E
E
20 1/2 1 i E
电磁场强度之间的关系
▪ 考虑外界电磁波垂直入射导体
v H
1
vv kE
1
v
iv
v E
良导体:Hv
i
e4
evn
v E
▪ 磁能密度与电场密度之比:
边界条件——精选推荐

一.边界条件(Boundry Conditions)1.理想电边界(Perfect-E)理想电边界即理想电导体边界.电荷可在其中自由移动.边界内电场为0,边界上可存在面电荷,面电流,从而使外界电场分量垂直与边界,磁场方向平行与边界. 在HFSS design中任何与背景相邻接的部分会被默认为Perfect-E边界(outer)对于矩形波导,若将波导终端端面设置为Perfect-E, 由于波导内电场平行于端面,在边界处被置0,即入射波与反射波在端面处摸值相等,相位相反,叠加为0,由于电压V是对电场强度的积分,因为边界处电场强度为0,则端面处电压为0,相当于终端短路(阻抗值Z=0,在阻抗圆图上表示短路点),VSWR趋于无穷大.(反射系数为1)H模截止频率为以下是对这一过程的仿真,其中矩形波导a=1.5mm, b=1mm,10λ=4.52267mm.取波导长度为100Ghz 取f=120Ghz 满足单模传输。
gλ,将端面设置为Perfect-E 进行测试。
18.09068mm=4*g图1-1 矩形波导主模传输终端设为Perfect-E时电场分布从图1-1可见在端面处电场切向方向为0,电场垂直于端面图1-2矩形波导主模传输终端设为Perfect-E时输入端Smith Chart可见负载端阻抗接近于开路。
L=1/4*g2.理想磁边界(Perfect-H)理想磁边界即理想磁导体,用电磁场理论中的磁荷模型进行分析即磁荷可以在理想磁导体自由移动,理想磁导体中磁场为0,边界上可聚集面磁荷,面磁流,从而使磁场方向垂直于边界。
电场方向与边界相切。
对应于矩形波导终端Perfect-H边界使得磁场垂直于边界,置切向磁场为0,由于电流Z趋向于是切向磁场的积分,故边界使电流为0,而切向电场存在,负载处电压不为0。
故L无穷,VSWR趋向于无穷,相当于终端开路。
以下是对这一过程仿真。
波导参数与上例中完全相同。
端面边界设置为Perfect-H.从图2-1中可看出端面处磁场垂直于端面,切向磁场分量为0。
电磁场与电磁波--电磁场的边界条件
cos(15
108
t)
20
cos(15108
t)]
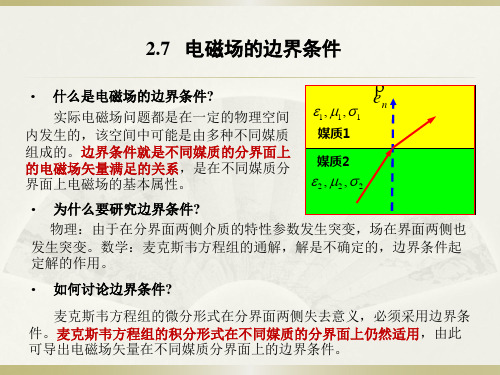
erx80cos(15108t) V/m
r E2
(0,
t
r ex
80
cos(15
108t)r exAcos(15
108
t)
)
V/m
V/m
z=0
r ez 媒质2
r ex
媒质1
2.7 电磁场的边界条件
利用两种电介质分界面上电场强度的切向分量连续的边界条件
电介质与自由空间 的分界面
rr r
r
rrr
ez {ex E1x ey E1y ez E1z [ex 2 y ey 5x ez (3 z)]} z0
r
r
ey (E1x 2 y) ex (E1y 5x) 0
则得
E1x 2 y, E1y 5x
r E2
r ex
2y
r ey 5z
r ez
r D
的法向分量连续
r B 的法向分量连续
r E 的切向分量连续
r H
的切向分量连续
1=0
ern
媒质1
媒质2
2
r D
、Br
的法向分量连续
2.7 电磁场的边界条件
2. 理想导体表面上的边界条件
D
• 理想导体:电导率为无限大的导电媒质 • 特征:电磁场不可能进入理想导体内 • 理想导体表面上的边界条件
r
r
l
rr H1 H2
r et
dl
r D
r
lim
h0
J dS
S
S
t
dS
媒质1
r r en Δl
电磁场理论知识点总结

电磁场理论知识点总结1.麦克斯韦方程组:麦克斯韦方程组是电磁场理论的核心方程,它由四个方程组成,分别是高斯定律、法拉第电磁感应定律、安培环路定律和法拉第电磁感应定律的积分形式。
这些方程描述了电场和磁场随空间和时间的变化规律。
2.电场和磁场的相互作用:根据麦克斯韦方程组,电场和磁场相互作用,通过电场的变化会产生磁场,而通过磁场的变化会产生电场。
这种相互作用是电磁波传播的基础。
3.电磁波的传播:根据麦克斯韦方程组的解,电磁波以光速在真空中传播,它是由电场和磁场相互耦合而成的波动现象。
电磁波的传播速度不同于物质中的电磁波传播速度,它是真空中的最大可能速度。
4.电磁感应现象:根据法拉第电磁感应定律,当一个导体中的磁场发生变化时,会在导体中产生感应电流。
这个现象被广泛应用于发电机、变压器等电磁设备中。
5.静电场和静磁场:当电荷和电流都不随时间变化时,产生的电场和磁场称为静电场和静磁场。
在静电场中,电场符合高斯定律;在静磁场中,磁场符合安培环路定律。
静电场和静磁场的研究对于理解电磁场的基本性质和应用具有重要意义。
6.电磁辐射和辐射场:根据麦克斯韦方程组的解,加速的电荷会辐射出电磁波。
这种辐射就是电磁辐射,它是电磁波传播的一种形式。
辐射场是指由电磁辐射产生的电场和磁场。
7.电磁波的频率和波长:电磁波的频率和波长是描述电磁波特性的两个重要参数。
频率指的是电磁波单位时间内振动的次数,单位是赫兹;波长指的是电磁波的一个完整振动周期所对应的空间距离,单位是米。
8.电磁场的能量和动量:根据电磁场的能量密度和动量密度的定义,可以推导出电磁场的能量和动量公式。
电磁场携带能量和动量,可以与物质相互作用,这是实现无线通信、光学传输等现代科技的基础。
9.电磁场的边界条件:电磁场在介质边界上的反射和折射现象可以通过电磁场的边界条件来描述。
边界条件包括麦克斯韦方程组的边界条件和介质的边界条件,它们确定了电磁场在边界上的行为和传播规律。
第3章媒质的电磁性质和边界条件

且
r ≈ 1
如金,银和铜等属于抗磁质. (2)顺磁质:磁化率为正,相对磁导率略大于1,即 = 1+ χ > 1 且 r ≈ 1 r m 如镁,锂和钨等属于顺磁质. (3)铁磁质:其磁化率非常大,其相对磁导率远大于1,即
r >> 1
如铁,镍和钴等属于铁磁质.
在铁磁性材料中,有许多小天然磁化区,称为磁畴.
电磁场与电磁波
第3章 媒质的电磁性质和边界条件 章
电介质的物态方程 5. 电介质的物态方程 电介质极化后,场域中除了自由电荷之外,又多了束缚电荷, 根据高斯定律: (ε 0 E ) = ρV + ρ P = ρV + ( P ) 可得: (ε 0 E + P ) = ρV 定义一个新矢量: D = ε 0 E + P
电磁场与电磁波
第3章 媒质的电磁性质和边界条件 章
四,媒质中的麦克斯韦方程组
积分形式 微分形式
D ) dS t
∫ ∫
l
H dl = ∫ ( J C +
S
l
E dl = ∫
S
B dS S t
D × H = JC + t B ×E = t
D = ρV
B = 0
∫
D dS = ∫ ρV dV
电磁场与电磁波
第3章 媒质的电磁性质和边界条件 章
3. 磁化强度 磁化强度的定义:单位体积内,所有磁矩的矢量和.
(A/m) V 磁介质被磁化后,磁介质中出现束缚电流. 束缚电流面密度: J mS = M × an′
V → 0
∑m M = lim
i
束缚电流体密度: J m = ′ × M 介质磁化后束缚电流在空间产生的矢量磁位:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电磁场的边界条件与电磁波的辐射和传播
[摘要]:本文结合相关示意图简要总结了电磁场的边界条件,在参考大量相关文献的基础上,由边界条件出发分析了交变电磁场传播的原理,联系实际解释了电磁场的辐射和传播。
关键字:电磁场;电磁波;边界条件;辐射;传播。
一、电磁场的边界条件
电磁场在两种不同媒质分界面上,从一侧过渡到另一侧时,场矢量E、D、B、H一般都有一个跃变。
电磁场的边界条件就是指场矢量的这种跃变所遵从的条件,也就是两侧切向分量之间以及法向分量之间的关系。
电磁场的边界条件可以由麦克斯韦方程组的积分形式推出,它实际上是积分形式的极限结果。
这些边界条件是:
n·(D1-D2)=ρs; (1)
n×(E1-E2)=0; (2)
n·(B1-B2)=0; (3)
n×(H1-H2)=J)s。
(4)
式中n为两媒质分界面法线方向的单位矢量,场矢量E、D、B、H的下标1或2分别表示在媒质1或2内紧靠分界面的场矢量,ρ为分界面上的自由电荷面密度,J为分界面上的传导电流面密度。
式(1)表示在分界面两侧电位移矢量D的法向分量的差等于分界面上的自由电荷面密度。
当分界面上无自由电荷时,两侧电位移矢量的法向分量相等,即其法向分量是连续的。
式(2)表示在分界面两侧电场强度E的切向分量是连续的。
式(3)表示在分界面两侧磁通密度B的法向分量是连续的。
式(4)表示在分界面两侧磁场强度H的切向分量的差等于分界面上的表面传导电流面密度。
当分界面上无表面传导电流时,两侧磁场强度的切向分量相等,即其切向分量是连续的。
当媒质2为理想导体时,E2、D2、B2、H2等于零,式(1)表示D1的法向分量等于自由电荷面密度;式(2)表示E1无切向分量.式(3)表示B1的法向分量为零;式(4)表示H1的切向分量等于表面传导电流面密度,并且与电流方向正交。
二、电磁波的辐射和传播
电磁波的产生与发射是通过天线来实现的。
由振荡电路产生的强大交变讯号通过互感耦合到天线上,天线就有交变电流产生,如下图所示。
此交变电流在天线周围激发交变磁场,交变磁场又激发交变的涡旋电场,交变的涡旋电场又反过来激发交变的涡旋磁场.如此相互激发产生电磁波并将其传播开去。
我们以天线上的交变电流变化一个周期为例,来说明电磁波的产生与传播过程。
如上图所示,当(a)图中天线上有向上的电流时,它激发的磁场环绕天线。
磁感应线从右边进入纸面,从左边穿出纸面。
对于具有相同大小磁感强度的空间各点,在天线两端的场点到天线轴线距离比天线中部的场点到天线轴线的距离要小些,以此为原则定性地画出了磁感应线的箭头“·”和箭尾“x”;当电流增加时,磁场也随之增大,由麦克斯韦涡旋电场的假说,此变化的磁场就激发涡旋电场,天线右边的电场线逆时针,左边的电场线顺时针,图(b)。
当电流达到极大值而后减小时,如前一时刻产生的闭合电场线已经传开。
由于电磁场的传播需要时间,这就使得当天线近处空间的磁场开始减小时,远处空间的磁场还在增加,它产生的电场的电场线的绕行方向仍与前一时刻靠近天线的电场线绕行方向相同。
比较图(b)与图(c)就清楚地看到了这一点,此时近处电场的电场线由于磁场减小使得在天线右边是顺是针,左边是逆时针,如图(c)所示。
当电流变小到反向时天线周围的磁场也跟着反向。
先前右边进,左边出的磁场已传向远方,不过由于近处磁场相对于右边进,左边出的方向来说仍是减小,故涡旋电场的电场线的方向不变,只是向外扩张,如图(d)所示。
只有当电流向下增大到极大值而反向减小时,电场的电场线的方向才反转过来,此时图(d)的电场线已向远处传播开去,如图(e)所示。
当电流反向减小到零而正向增大时,电流变化完成一个周期,电磁场的传播如图(f)所
示。
这便又开始了从图(b)到(f)的过程,如此周而复始地将电磁波产生与传播开去。
如果将电磁波传播的空间图象的一个波长与波源处B变化一个周期对应起来,就得出图3。
取天线中电流为零的时刻为一个周期的开始,此时波源处的B为零一个周期终了之后,该周期开始时波源激发的B传得最远,对应电磁波传播一个周期的图象应是电磁波的波前,即图(4)中圆形虚线。
通过以上电磁波的产生与传播过程的分析可以清楚地看到:
(1)天线上交变电流激发交变磁场,交变磁场又激发交变电场,很明显交变电磁场是与天线中交变电流具有相同周期的周期函数。
(2)从图4中的A,C,D三点处的电场E,磁场B来看,A处因两边电场线的绕行方向相反,使得它的电场线同向,E向下最大,此时B也恰好向里最大;在C点处,因两边电场线的绕行方向相同,使得它的电场线方向相反,E为零,B也恰好为零;D点处因两边的电场线绕行方向相反,它的电场线同向,E向上最大,此处B也恰好向外最大,这就说明,电磁波中电场E,磁场B的变化是同步的。
( 3)从图3或图4中,我们还可以清楚地看到磁场H与电场E是相互垂直的,并且垂直于电磁波的传播方向,说明电磁波是横波.同时从图4A处的电场E(方向向下,沿y 轴负向),磁场H(方向向内,沿z轴负向),与传播方向即波速:(方向向右,沿x轴)的关系看,E,H,:不仅相互垂直,而且互成右手螺旋,从D点也可以看出这点,这就说明:
v的方向是EXH的方向。
( 4)对于一给定天线发射的电磁波,在某一给定的传播方向上,电场磁场的振动方向各自总是一定的,如图3所示,磁场振动方向总是垂直于纸面,电场振动方向总是平行于纸面,也就是说电磁波具有偏振性。
参考文献:
[1]何文质.关于电磁场边界条件的另一种合适推求[J].河北机电学院学报,1991年第8卷第1期:80~86.
[2]黄明哲.电磁波的传播与辐射[J].高等函授学报(自然科学版),1996年第4期:37~39.
[3]杜晓燕,杨明珊,张秀钢.关于电磁场边界条件教学的几点思考[J].电气电子教学学报,2011年第33卷第4期:112~117.
[4]张洪欣.电导率有限媒质分界面电磁场的边界条件[J].吉首大学学报(自然科学版),2007年第28卷第2期:48~50.。
