角加速度及转动惯量计算公式
刚体角动量公式

刚体角动量公式角推力理论:M=ia=I*(DW/DT)=D(IW)/DT=DL/DT,M为扭矩,I为惯性时间,a为角加速度。
DW/DT是导数,W是加速度,t是时间。
=IW是角动量,表明对于绕固定轴旋转的刚体,其角运动的变化速度等于作用在刚体上的外部对。
这是角力矩的理论。
角动量守恒定律的右边:从刚体角运动理论的公式中可以看出,刚体角运动的变化是由外部刚体对的作用引起的。
对于对角动量守恒,这个表达式的物理意义是,当物体的外力矩M等于零时,物体的角动量J=常数。
换句话说,物体的旋转也有惯性。
只要外副等于零且惯性矩保持不变,物体的旋转速度和方向就保持不变。
物体的旋转效果在外力或内力作用下不会发生变化,直到外力作用下,物体的旋转效果才会发生变化角动量守恒实际上成对相等。
例如,八颗行星离太阳越远,行星线速度越慢;事实上,力臂越长,地球上的力就越小。
另一个例子是把绳子系在石头上。
同样的力,绳子越长,石头越慢;相反,石头越快。
这是强度和角动量守恒定律。
另一个例子是普通自行车的后轮。
当最小值出现时,很难停止,因为车轮每个点两侧的力矩相等,并且由相互限制产生的角动量保持不变,而其他摩擦力和阻力非常小,因此很难停止。
因此,一些车轮对它们进行配重,以找到平衡,从而使力偶相等,并保持角动量。
也就是说,行星角动量守恒,也就是说,太阳自转产生的能量守恒,也就是说,这对行星与太阳自转的能量一致,或者说达到平衡,从而使行星永远围绕太阳自转在物理学中,角动量是一个物理量,与物体在原点的运动和动量有关。
角动量用经典力学表示,例如运动到原点与动量的叉积。
角推力是一个矢量。
角动量在不受外界影响时保持不变。
角运动和角是量子力学中结合的一对物理尺寸。
角动量中L = mvl 怎么来的首先需要了解,角动量(angularmomentum)在物理学中是和物体到原点的位移和动量相关的物理量。
它表征质点矢径扫过面积速度的大小,或刚体定轴转动的剧烈程度。
常用物体的转动惯量与扭矩的计算
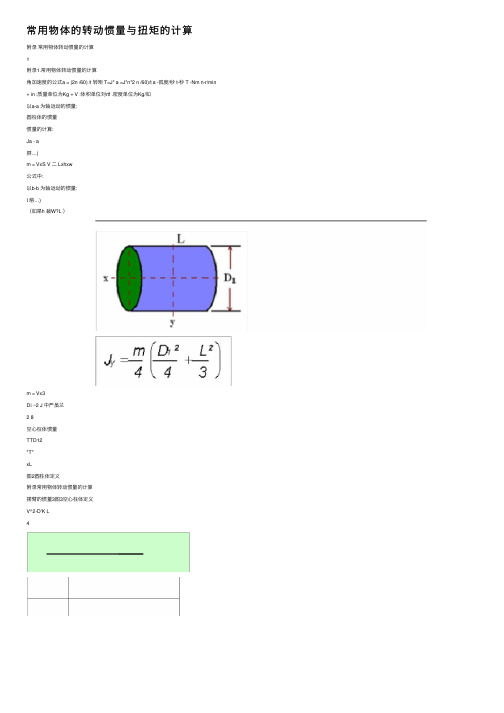
常⽤物体的转动惯量与扭矩的计算
附录常⽤物体转动惯量的计算
1
附录1.常⽤物体转动惯量的计算
⾓加速度的公式a = (2n /60) /t 转矩 T=J* a =J*n*2 n /60)/t a -弧度/秒 t-秒 T -Nm n-r/min + in :质量单位为Kg + V :体积单位対rtf .密度单位为Kg/如
以a-a 为轴运动的惯量:
圆柱体的惯量
惯量的计算:
Ja - a
摂…)
m = VxS V ⼆ Lxhxw
公式中:
以b-b 为轴运动的惯量:
I 熔…)
(如杲h 裁W?L )
m = Vx3
Di ~2 J 中严虽兰
2 8
空⼼柱体惯量
TTD12
"T"
xL
图2圆柱体定义
附录常⽤物体转动惯量的计算
摆臂的惯量3图3空⼼柱体定义
V^2-D'K L
4
图4-1摆臂1结构定义
J = m.R3
曲柄连杆的惯量
附录常⽤物体转动惯量的计算
带减速机结构的惯量5图5曲柄连杆结构定义J = m R2 + mi ri2
齿形带传动的惯量
J N :电或量 J L :负载惯量
J LOH :负载惯量折茸到电机侧前慣
量
M L :负载转矩
J R :减速机折算到输⼊的15量 R :减速⽐
H K :喩速机效率
R=
6JW = X Bf = ff X 0)L
&L 3L
■根爵能量守恒定律:
图6带减速机结构定义Jx 丁⼆ J M + J R Z ,■总惆
齿形带传动的惯量。
转动惯量与角加速度的关系

转动惯量与角加速度的关系转动惯量和角加速度是描述物体旋转运动特性的两个重要物理量。
转动惯量是物体对于旋转轴的惯性特性,与物体的质量分布和旋转轴的位置有关。
角加速度则描述了物体在旋转过程中角速度的变化率。
本文将探讨转动惯量与角加速度之间的关系,并说明它们在物理学中的应用。
一、转动惯量的定义转动惯量是物体对于旋转轴的分布的一种量度,用 I 表示。
在刚体整体旋转时,转动惯量与物体的质量分布密切相关。
对于具有质量为m 的质点,其转动惯量可以用其到旋转轴的距离 r 平方乘以质量来表示,即 I = mr^2。
对于质点系,其转动惯量是各个质点转动惯量之和。
二、角加速度的定义角加速度是物体在单位时间内角速度的变化量,用α 表示。
角加速度与转动惯量之间存在着紧密的关系。
物体的角加速度为单位时间内角速度的变化量,可以由牛顿第二定律推导得出,即α = τ/I,其中τ 表示物体所受到的转矩。
三、转动惯量与角加速度的关系由上面的公式可以看出,转动惯量与角加速度成反比。
具体而言,当转动惯量增大时,物体的角加速度减小;反之,当转动惯量减小时,物体的角加速度增大。
这是因为转动惯量越大,对于给定大小的转矩,物体的角加速度就越小;相反,当转动惯量较小时,给定大小的转矩将导致较大的角加速度。
四、转动惯量与角加速度的应用转动惯量与角加速度的关系在实际应用中具有广泛的意义。
以下是几个例子:1. 滚动体的加速度计算:当一个物体滚动时,其转动惯量与角加速度的关系可以用来计算物体的加速度。
通过测量物体的转动惯量和应用力矩的大小,我们可以得到该物体的角加速度,从而计算出物体的加速度。
2. 刚体的角速度变化:当一个刚体绕固定轴进行旋转时,转动惯量与角加速度的关系可以帮助我们分析刚体的角速度变化。
通过改变刚体的转动惯量,或者改变施加在刚体上的力矩,我们可以控制刚体的角加速度,从而实现对角速度的控制。
3. 转动惯量的测量:在实验室研究中,我们经常需要测量物体的转动惯量。
转动惯量 角加速度

转动惯量角加速度转动惯量和角加速度是物理学中两个重要的概念。
它们与旋转运动有关,揭示了物体在旋转过程中所表现出的惯性和加速度特性。
本文将详细介绍转动惯量和角加速度的基本概念、计算方法以及其在实际应用中的意义。
一、转动惯量的概念转动惯量,也称为转动惯性矩,是描述物体抵抗转动的惰性的物理量。
它表示了物体绕轴线旋转时所表现出的抵抗力度,类似于物体质量在直线运动中表现出的惯性作用。
转动惯量的大小取决于物体的质量分布以及轴线与物体几何形状的关系。
对于质点,其转动惯量的计算公式为I = mr^2,其中m为质点的质量,r为质点到旋转轴的距离。
对于刚体,由于其形状复杂,转动惯量的计算需要使用积分或几何分析方法,常见的刚体转动惯量公式有如下几种:1. 球体:I = (2/5)mR^2,其中m为球体的质量,R为球体的半径。
2. 圆柱体:I = (1/2)mR^2,其中m为圆柱体的质量,R为圆柱体的半径。
3. 长方体:I = (1/12)m(a^2 + b^2),其中m为长方体的质量,a 和b分别为长方体的长和宽。
需要注意的是,转动惯量是一个正定的物理量,它的单位为kg·m^2。
二、角加速度的概念角加速度是角速度随时间的变化率,表示物体在旋转过程中角速度的加速度。
与线性加速度类似,角加速度描述了物体旋转速度的变化情况,其符号和大小与角速度的变化方向和速率有关。
角加速度的计算公式为α = Δω/Δt,其中α表示角加速度,Δω表示角速度的变化量,Δt表示时间的变化量。
在匀加速旋转中,角加速度可以通过物体转过的角度和所需时间的关系来计算,即α =Δθ/Δt,其中α表示角加速度,Δθ表示物体转过的角度,Δt表示所需时间。
三、转动惯量与角加速度之间的关系转动惯量和角加速度之间存在一种基本的关系:牛顿第二定律在旋转运动中的推广形式,即τ = Iα,其中τ表示力矩,I表示转动惯量,α表示角加速度。
根据这个公式,我们可以看出,当给定力矩τ和转动惯量I时,可以求解出相应的角加速度α。
如何计算物体的旋转惯量和角加速度?

如何计算物体的旋转惯量和角加速度?
要计算物体的旋转惯量和角加速度,首先需要了解一些基本概念。
物体的质量分布和转动轴的位置决定了物体的转动惯量,它表示物体转动时需要施加的力矩的大小。
而角加速度则是描述物体转动速度变化的物理量,它等于物体角速度的变化量与时间的变化量的比值。
计算旋转惯量的一般公式是:I =∫r²dm,其中r是质量微元dm 到转动轴的距离,积分范围是整个物体的质量分布。
通过这个公式,我们可以计算出物体相对于任意轴的转动惯量。
而计算角加速度的公式则比较简单,它等于力矩除以转动惯量,即α=M/I。
力矩M等于施加的力与力臂的乘积,它使物体产生旋转运动。
通过测量力矩和转动惯量,就可以计算出角加速度。
在实际应用中,计算物体的旋转惯量和角加速度需要注意以下几点:首先,选择合适的转动轴,它可以是物体的重心或者特定的几何轴线;其次,精确测量物体的质量分布和力臂长度;最后,注意单位的统一,保证计算结果的准确性。
通过以上步骤,我们可以计算出物体的旋转惯量和角加速度,为进一步研究物体的动力学特性和运动规律提供基础。
这些计算方法不仅适用于机械系统,也适用于各种物理和工程领域,具有广泛的应用价值。
常用物体的转动惯量-与扭矩的计算

常用物体的转动惯量-与扭矩的计算附录1.常用物体转动惯量的计算图i 矩形结构定义以a-a 为轴运动的惯量:以b-b 为轴运动的惯量:圆柱体的惯量惯量的计算:矩形体的计算 b角加速度的公式a = (2n /60 ) /t 转矩T=J* a =J*n*2 n /60 ) /ta -弧度/秒 t-秒 T - Nm n-r/minm 3为为为位位位 单单单 量积度 质体密m VJa - a公式中:m = VxSV = Lxhxw12(4L 2 + w 2)图2圆柱体定义m = Vx6V=^L4Dir =—2 J宙严二叱匹2 8m(D^_1 W空心柱体惯量m = Vx34m /(P O 2+D 2')+L 2>~4 \4 +_1 >Jx =m x (Do 2+DF)Do图3空心柱体定义少”)图4-1摆臂1结构定义图4-2摆臂2结构定义J = m.R2J = m R? + rm n2图5曲柄连杆结构定义J M:电机惯量J L :负載惯量J L<SM :负载惯量折算到电机侧的惯量M L:负载;转矩J R :减速机折算到输入的愤量R :减速比r]R:减速机效率R= — = - 8M = 3W=R X3L9L 3L■总惯量:J IV!4* J R +J I r 阳■根据能量守恒定律;■折算到电机側的力矩:— = —图6带减速机结构定义J M :电机惯量 J L :负载惯量 Mi :负载力矩 Jp M :电机侧带轮惯量 D PM :电机侧带轮直径 N TM :电机側带轮齿数J PL :负载侧带轮惯量 □PL :负载带轮直径N TL :负载带轮齿数图7齿形带传动结构■总惯量:J TQ T= J 藝+ J 刖+ J 牡T M 斗J B -皿+ Z T 射■折算劃电机惯量:訂t 鑿心檢鷺翻,W 加囂。
zq■折算到电机扭矩:尿…IVk g = wDn r) R /)时7>q :减速机效率me :皮带质量J 叫叭皿6ljwljmlJ P L J Dp —6M = /?x Q L CO JW = R XCJ J L D PLJ M :电机惯量J L :负载」惯量M L :负载扭矩J GM :电机側齿轮惯量N IM :电机侧齿轮齿数J GL :负载齿轮惯量N R:负载齿轮齿数n:减速机效率R =——0/M = R^Q L COM= /?x torN TM■总惯量:■折算到电机惯量:■折算到电机力矩; .. .. ... ... .. .. ... ... .. .. ... ... ..N刑M LS^=M L--- = ----/) Rrj图8齿轮组传动结构J M :电机惯量Jc :连接轴惯量ITlL :负载质量XL:负载位置VL:负载速度ITIT :滑台质量FP:做功力Fg :重力Ffr:摩擦力Js :丝杠惯量p :丝杠螺距(mm/rev)a:丝杠角度n:丝杠效率P:摩擦系数g:重力加速度图9丝杠传动结构■总惯量:i/ror™ J M + Jc + Js + J L何“ (片+斤+耳)P折算到电机的惯量:折算到电机的力矩GJ M -——W MC PI =TTD I =N/Pip G M _X LC PIV L3怖=------cpiJu :电机惯量mL:负载质量XL:负载位置V L :负载速度mo :传送带质量FP:作用力Fg :重力Frr :摩擦力jpx :辗轴惯量Dx :辗轴直径N TPI :主辐齿数p :传送带导程(mm/tooth)Cpi :主银周长a :倾角n:传送带效率P:摩擦系数g:引力系数图10传送带结构liliii瓦2出D:总惯量折算到电机的惯量曲 *(Fp + Fg + F 柠)D心x — /} 2E = \mL + mB)xgxsina H = (me + mjx g x “ x cosa图11齿轮齿条结构定义■总惯量:J TOT —+ J G 4- J L■折算到电机的惯量:C G = TTD G = N repsG M =—C GV L3M =——J 帕:电机惯量 rriL:负载质量X L :负载位置 V L :负载速度F P :作用力 耳:重力 Ffr :摩擦力J G :齿轮惯量 D G :齿轮宜径N TG :齿轮齿数pc :齿轮导程(mm/tooth) C G :齿轮周长a :轴运动角度 q :齿轮传动效率 p:摩擦系数齿轮,齿条传动惯量的计算M T■折算到电机的力矩:1,确认您的负载额定扭矩要小于减速机额定输出扭矩,2,伺服电机额定扭矩*减速比要大于负载额定扭矩。
转动力矩与角加速度

转动力矩与角加速度在物理学中,转动力矩和角加速度是涉及刚体旋转的两个重要概念。
转动力矩描述了一个力对刚体旋转的产生影响,而角加速度则代表了刚体旋转的变化速率。
本文将探讨转动力矩和角加速度的定义、计算公式以及它们之间的关系。
一、转动力矩的定义和计算转动力矩,也称为转矩或扭矩,是指力对刚体旋转产生的影响。
它与力的大小、作用点与旋转轴的距离以及力的方向有关。
根据力矩的定义,转动力矩可以表示为:τ = F × r × sinθ其中,τ表示转动力矩,F是作用在刚体上的力的大小,r是力作用点到旋转轴的距离,θ是力的方向与力臂之间的夹角。
转动力矩的单位是牛顿·米(N·m)。
当力的方向与力臂垂直时,力矩达到最大值;当力的方向与力臂平行时,力矩为零。
例如,一个力为20牛顿的力作用在一个距离旋转轴2米的刚体上,与力臂夹角为30度。
那么该力对旋转的转动力矩可以通过公式计算:τ = 20 × 2 × sin30° = 20 × 2 × 0.5 = 20 N·m二、角加速度的定义和计算角加速度代表了刚体旋转过程中的变化速率。
它与刚体所受的力矩和刚体的转动惯量有关。
角加速度的定义可以表示为:α = τ / I其中,α表示角加速度,τ表示转动力矩,I表示刚体的转动惯量。
转动惯量是描述刚体对于旋转的惯性大小的物理量,它与刚体的质量分布和几何形状有关。
不同几何形状和质量分布的刚体具有不同的转动惯量。
角加速度的单位是弧度/秒²。
它的正负号代表了刚体旋转的方向,根据右手法则,顺时针旋转的角加速度为负值,逆时针旋转的角加速度为正值。
例如,一个质量为2千克的刚体,受到了转动力矩为30 N·m的作用。
已知该刚体的转动惯量为4 kg·m²。
可以通过公式计算角加速度:α = 30 N·m / 4 kg·m² = 7.5 rad/s²三、转动力矩与角加速度的关系转动力矩与角加速度之间存在着直接的关系。
常用物体转动惯量-与扭矩计算
1 / 12附录1.常用物体转动惯量的计算角加速度的公式a = (2n /60) /t 转矩 T=J* a =J*n*2 n /60) /t a -弧度/秒 t-秒 T -Nm n-r/min图i 矩形结构定义以a-a 为轴运动的惯量:m = VxS V =Lxhxw公式中:以b-b 为轴运动的惯量:圆柱体的惯量惯量的计算:/ WI■bm 3 为为为位位位 单单单 量积度 质体密12(4L 2+w 2) 矩形体的计算Ja - a图2圆柱体定义m = Vx§TTD12V = ------ XL4Dir =—2mx[>(Dt2空心柱体惯量摆臂的惯量3 / 12m = Vx34m /(P O 2+D 2')+ L 2>~4 \ 4 +_1 >图3空心柱体定义Jx =m x (Do 2+DF) 8曲柄连杆的惯量图4-1摆臂1结构定义图4-2摆臂2结构定义J = m.R2带减速机结构的惯量5 / 12J = m R? + rm n2图5曲柄连杆结构定义齿形带传动的惯量J M :电机惯量J L :负載惯量J L <SM :负载惯量折算到电机侧的惯量 M L :负载;转矩J R :减速机折算到输入的愤量R :减速比r]R :减速机效率R= — =- 8M = 3W = R X 3L9L 3L图6带减速机结构定义■总惯量:J IV ! 4* J R + J Ir 阳■根据能量守恒定律;■折算到电机側的力矩:— = —J 叫叭皿6ljwljmlJ M :电机惯量 齿轮组减速结构的惯量7 / 12J L :负载惯量Mi :负载力矩Jp M :电机侧带轮惯量 D PM :电机侧带轮直径 N TM :电机側带轮齿数J PL :负载侧带轮惯量 □PL :负载带轮直径N TL :负载带轮齿数图7齿形带传动结构■总惯量:J TQ T=J 藝+ J 刖+J 牡T M 斗J B -皿+Z T射■折算劃电机惯量:訂t 鑿心檢鷺翻,W 加囂。
