加速度与位移
位移速度加速度概念梳理
位移速度加速度概念梳理在物理学中，位移、速度和加速度是三个非常重要的概念，它们帮助我们描述物体的运动状态和运动过程。
让我们一起来深入理解一下这三个概念。
首先，位移是描述物体位置变化的物理量。
想象一下，有一个物体从 A 点移动到了 B 点，那么从 A 点指向 B 点的有向线段就是物体的位移。
位移不仅有大小，还有方向，是一个矢量。
比如说，一个人从家走到学校，走的路径可能弯弯曲曲，但位移就是家到学校的直线距离，并且方向是从家指向学校。
与位移容易混淆的是路程。
路程是物体运动轨迹的长度，只有大小没有方向，是一个标量。
举个例子，一个人绕着操场跑了一圈，他跑过的轨迹长度就是路程，但位移是零，因为他最终回到了起点，位置没有发生变化。
接下来，我们谈谈速度。
速度是用来描述物体运动快慢和方向的物理量。
它等于位移与发生这个位移所用时间的比值。
如果一个物体在一段时间内的位移是Δx，所用时间是Δt，那么速度 v 就等于Δx/Δt 。
速度同样是矢量，既有大小又有方向。
日常生活中，我们常常说的“速度”，很多时候其实指的是速率。
速率是物体运动的路程与所用时间的比值，只有大小没有方向，是标量。
比如，汽车仪表盘上显示的速度通常是速率。
再来说说平均速度和瞬时速度。
平均速度是在一段时间内的位移与时间的比值，反映的是物体在这段时间内运动的平均快慢程度。
而瞬时速度是物体在某一时刻或某一位置的速度。
当时间间隔非常非常小的时候，平均速度就趋近于瞬时速度。
举个例子，一辆汽车在一小时内行驶了 60 公里，那么这一小时内的平均速度就是 60 公里每小时。
但如果我们想要知道汽车在某个瞬间的速度，比如通过测速摄像头时的速度，那就是瞬时速度。
最后，我们来了解一下加速度。
加速度是描述物体速度变化快慢的物理量。
它等于速度的变化量与发生这一变化所用时间的比值。
如果物体的速度在Δt 时间内从 v1 变化到 v2 ，那么加速度 a 就等于（v2v1)／Δt 。
加速度也是矢量，它的方向与速度变化量的方向相同。
加速度与位移关系式
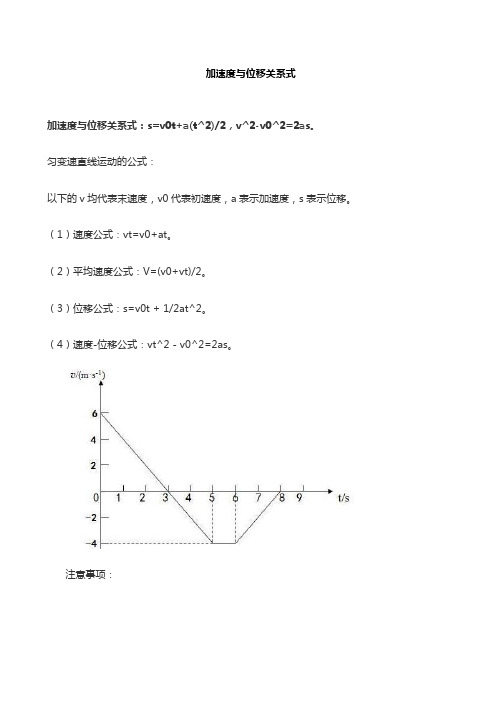
加速度与位移关系式
加速度与位移关系式：s=v0t+a(t^2)/2，v^2-v0^2=2as。
匀变速直线运动的公式：
以下的v均代表末速度，v0代表初速度，a表示加速度，s表示位移。
（1）速度公式：vt=v0+at。
（2）平均速度公式：V=(v0+vt)/2。
（3）位移公式：s=v0t + 1/2at^2。
（4）速度-位移公式：vt^2 - v0^2=2as。
注意事项：
1、当物体的加速度保持大小和方向不变时，物体就做匀变速运动。
如自由落体运动、平抛运动等。
当物体的加速度方向与初速度方向在同一直线上时，物体就做匀变速直线运动。
如竖直上抛运动。
2、加速度可由速度的变化和时间来计算，但决定加速度的因素是物体所受合力F和物体的质量M。
3、加速度与速度无必然联系，加速度很大时，速度可以很小；速度很大时，加速度也可以很小。
例如：炮弹在发射的瞬间，速度为0，加速度非常大；以高速直线匀速行驶的赛车，速度很大，但是由于是匀速行驶，速度的变化量是零，因此它的加速度为零。
4、加速度为零时，物体静止或做匀速直线运动（相对于同一参考系）。
任何复杂的运动都可以看作是无数的匀速直线运动和匀加速运动的合成。
速度加速度和位移的关系
速度加速度和位移的关系在物理学中，速度、加速度和位移是描述物体运动状态和变化的关键概念。
它们之间存在着紧密的关系，这种关系对于理解物体在空间中的运动轨迹和运动特性非常重要。
本文将探讨速度、加速度和位移之间的关系，并深入介绍它们在物理学中的应用。
一、速度、加速度和位移的定义在开始讨论它们之间的关系之前，我们先来看一下它们的定义。
1. 速度（velocity）：速度是物体在单位时间内所移动的距离。
它是一个矢量量，既有大小也有方向。
速度的单位通常是米每秒（m/s）。
2. 加速度（acceleration）：加速度是物体在单位时间内速度的变化率。
它也是一个矢量量，既有大小也有方向。
加速度的单位通常是米每平方秒（m/s²）。
3. 位移（displacement）：位移是指物体从一个位置到另一个位置所经过的路径长度的变化量。
它是一个矢量量，有大小和方向。
位移的单位通常也是米（m）。
二、速度加速度和位移之间的关系速度、加速度和位移之间的关系可以通过微积分的概念来理解。
根据微积分的定义，速度是位移对时间的导数，加速度是速度对时间的导数。
换言之，速度和加速度可以分别表示为位移和时间的一阶导数和二阶导数。
1. 速度和位移的关系根据速度的定义，速度等于位移除以时间。
数学表达式为：速度 = 位移 / 时间即v = ∆x / ∆t这个公式告诉我们，速度可以通过位移和时间来计算。
例如，一个物体从位置A移动到位置B，所经过的位移为∆x，所花费的时间为∆t，那么它的速度就等于∆x除以∆t。
2. 加速度和速度的关系根据加速度的定义，加速度等于速度除以时间。
数学表达式为：加速度 = 速度 / 时间即a = v / ∆t同样，这个公式告诉我们，加速度可以通过速度和时间来计算。
例如，一个物体在某一瞬间的速度为v，经过的时间为∆t，那么它的加速度就等于v除以∆t。
三、速度、加速度和位移的应用速度、加速度和位移是物理学中的重要概念，它们在许多实际应用中都有广泛的应用。
加速度公式与位移公式
加速度公式与位移公式匀加速直线运动中，加速度是恒定不变的，速度与时间成正比，即： vt = vo + at这是匀加速运动的定义式，现推导匀加速直线运动的位移公式。
位移是速度的叠加，设单位时间内的瞬时速度为vt，则单位时间内的位移ds为vtdt，由vt = vo + a速度v,速度变化量v,加速度a的区别和联系. 如何认知物体运动的快慢和运动速度变化的快慢?物体运动的快慢是指物体位置变化的快慢，用速度来描述，速度越大就说明物体运动得越快；物体由静止到运动或由运动到静止，其速度都发生变化。
有的物体速度变化的快，如子弹发射，有的物体速度变化得慢，如列车启动，加速度就表示速度变化的快慢。
. 如何认知速度的变化量和速度的变化率（加速度）①速度的变化量是指速度改变了多少，它等于物体的末速度和初速度的矢量差，即，它是一矢量，表示速度变化的大小和方向。
②加速度（速度的变化率）就是指速度的变化量与出现这一变化所用时间的比值，在数值上等同于单位时间内速度的变化量。
加速度叙述的就是速度变化的快慢，其大小由速度变化量和出现这一变化所用的时间共同同意。
加速度的方向与速度变化量方向相同。
③加速度与速度的大小及速度变化的大小无必然联系。
加速度大表示速度变化快，并不表示速度大，也不表示速度变化大。
比如，小汽车启动时加速度非常大，速度却不大，当小汽车高速行驶时，速度非常大，加速度却不大，甚至为零。
④加速度是矢量，它的方向与速度的变化△ 方向相同，与速度的方向无必然联系，a 可以与速度方向相同，也可以相反，还可以成一夹角。
.如何认定物体搞加速运动还是搞减速运动？根据加速度和速度两方向间的关系。
只要加速度方向和速度方向相同,就是加速；反之就是减速。
这与加速度变化和加速度的正、负无关。
可以总结如下：匀加速运动中：a 越大，v减少得越慢a 和v 同向加速运动a越大，v 减少得越慢匀减速运动中：a减小，v增大得慢a和v反向减速运动a增大，v增大得加速度越来越小，速度却可以越来越大，只能说速度增加得越来越慢。
位移速度与加速度的关系
位移速度与加速度的关系在物理学中，位移速度和加速度是描述物体运动的重要概念。
位移速度指的是物体在单位时间内所产生的位移，而加速度表示单位时间内速度变化的大小。
位移速度与加速度之间存在着一定的关系，这在动力学中被广泛应用和研究。
一、位移速度的定义和计算方法位移速度是指物体在单位时间内所产生的位移量。
其计算方法可以通过求解物体在运动过程中的位移和时间的比值来得到，常表示为v。
例如，当一个物体从A点移动到B点时，其所产生的位移量为s，所用的时间为t，则位移速度v的计算公式为v=s/t。
二、加速度的定义和计算方法加速度是指单位时间内速度发生的变化量。
其计算方法可以通过求解物体在运动过程中速度的变化量与时间的比值来得到，常表示为a。
例如，当一个物体由静止开始加速运动时，其速度从开始时的0增加到某一数值v，所用的时间为t，则加速度a的计算公式为a=v/t。
三、位移速度与加速度的关系根据物理学中的运动学公式，位移速度、初始速度、加速度和时间之间存在着如下关系：v = u + at其中，v表示末速度，u表示初始速度，a表示加速度，t表示时间。
由上述公式可以看出，位移速度的大小与初始速度、加速度和时间紧密相关。
当初始速度为0时，位移速度与加速度的关系可以简化为：v = at这意味着位移速度与加速度成正比，随着加速度的增大，位移速度也会相应增加。
当加速度为正值时，位移速度将随着时间的增加而逐渐增大；当加速度为负值时，位移速度将随着时间的增加而逐渐减小。
四、利用位移速度与加速度的关系解决实际问题在实际应用中，我们可以利用位移速度与加速度的关系来解决一些与运动有关的问题。
例如，我们可以根据已知的加速度和时间，计算出物体在运动过程中所产生的位移速度；或者根据已知的位移速度和时间，计算出物体所受的加速度大小。
在交通工程中，位移速度和加速度的关系也得到了广泛的应用。
通过研究车辆的位移速度和加速度变化规律，可以优化交通信号控制系统，提高交通效率，减少交通拥堵。
加速度位移时间的关系
加速度位移时间的关系加速度、位移和时间是物理学中非常重要的概念。
它们之间的关系可以通过牛顿第二定律以及基本运动学公式来描述。
首先，加速度是一个描述物体运动变化率的物理量，它定义为单位时间内速度的变化量。
在一维运动中，加速度可以根据物体的速度变化情况来表示。
如果一个物体在某个时间段内的速度发生变化，那么它的加速度就可以通过以下公式来计算：加速度(a) = (Vf - Vi) / t其中，Vf是时间段结束时物体的速度，Vi是时间段开始时物体的速度，t是时间段的持续时间。
位移是一个描述物体位置变化的物理量，它定义为物体从一个位置到另一个位置之间的距离。
在一维运动中，位移可以通过以下公式计算：位移(d) = (Vf + Vi) / 2 * t其中，Vf和Vi分别是时间段结束时和开始时的速度，t是时间段的持续时间。
时间是物体运动的一个重要参量，它可以通过测量运动开始和结束的时间来确定。
从上述公式可以看出，加速度、位移和时间之间存在一种关系：位移等于速度的平均值乘以时间。
由于加速度定义为速度的变化率，所以可以将速度的平均值写为Vi + (Vf - Vi) / 2，从而得到位移公式。
此外，我们还可以从牛顿第二定律的角度来看待加速度、位移和时间的关系。
牛顿第二定律表明，物体的加速度等于作用在物体上的力与物体的质量的比值。
根据牛顿第二定律，我们可以推导出以下公式：加速度(a) = F / m其中，F是作用在物体上的力，m是物体的质量。
由此可见，在已知物体的质量和受力情况的前提下，我们可以计算出物体的加速度。
然后，根据位移公式，我们可以根据已知的加速度和时间来计算位移。
总结起来，加速度、位移和时间之间存在着紧密的关系。
通过运用牛顿第二定律、基本运动学公式以及已知的力、质量、速度和时间等信息，我们可以推导出加速度、位移和时间之间的关系式，从而更好地理解和描述物体的运动特性。
运动的描述位移速度与加速度
运动的描述位移速度与加速度运动的描述：位移、速度与加速度运动是物体在空间中变换位置的过程，我们可以通过位移、速度和加速度等概念来描述运动。
一、位移位移是指物体从初始位置到最终位置之间的位置变化量。
它是矢量量值，包括方向和大小。
通常用符号Δs表示。
位移可以用直线、曲线等方式表示，具体取决于物体运动的轨迹。
在直线运动中，位移的大小等于物体最终位置与初始位置之间的距离，即Δs = s终 - s初。
如果物体回到了起始位置，位移等于零，即Δs = 0。
在曲线运动中，位移的计算稍微复杂一些。
我们可以将轨迹分成无穷小的小段，然后对每个小段的位移进行累加，得到整个曲线运动的位移。
二、速度速度是指物体单位时间内位移的变化率，描述了物体运动的快慢和方向。
速度是矢量量值，包括大小和方向。
速度的大小通常用符号v表示。
平均速度是指物体在某段时间内的位移与时间的比值。
平均速度的计算公式为v平均= Δs / Δt，其中Δs是位移，Δt是时间。
瞬时速度是指物体某一瞬间的速度，即极限速度。
瞬时速度可以通过求取极限来计算，也可以通过计算物体位移的微小变化量除以时间的微小变化量来近似计算。
在直线运动中，速度的方向与位移的方向一致。
在曲线运动中，速度的方向则沿着运动轨迹的切线方向。
三、加速度加速度是指单位时间内速度的变化率，描述了物体运动的加速或减速情况。
加速度也是矢量量值，包括大小和方向。
加速度的大小通常用符号a表示。
平均加速度是指物体在某段时间内速度的变化量与时间的比值。
平均加速度的计算公式为a平均= Δv / Δt，其中Δv是速度的变化量，Δt 是时间。
瞬时加速度是指物体某一瞬间的加速度，即极限加速度。
瞬时加速度的计算方法与瞬时速度类似，可以通过求取极限或近似计算。
加速度的方向的变化可能与速度的方向一致，也可能与速度的方向相反。
例如，在向右运动的物体突然向左减速，加速度的方向将指向左侧。
四、位移、速度和加速度之间的关系位移、速度和加速度之间存在着密切的联系。
位移、速度、加速度
1-1-2
２、速度 Velocity 瞬时速度、简称速度： v = lim t→0 r/ t = dr/dt 速度方向为所在点轨迹的切线方向，并 指向质点前进的一方 在直角坐标系中 v = dx/dt i + dy/dt j + dz/dt k 速度分量 vx = dx/dt , vy = dy/dt , vz = dz/dt 速度的大小： | v | = ( vx2 + vy2 + vz2 )1/2
1-1-2
v(t) P Q ρ no dθ
v(t+dt)
O vdθ v(t) v(t+dt) dv dv
1-1-2
dv = dv to + vd no 所以 vdt =ρd 故 d /dt = v /ρ 将上式两边除以dt可得质点在P点的加速度 a = dv/dt = dv/dt to + vd /dt no = dv/dt to + v2/ρ no dv/dt 为沿切向分量，故称为质点的切 向加速度 at ，其值等于速率的变化率，它 表示速度变化的快慢。
例1-2 有一质点沿x轴作直线运动为 x(t) = 4.5t2 - 2t3 (SI)，试求: (1)第2秒内的平均速度 v， (2)第2秒末的速度 v， (3)第2秒内经过的路程s 及平均速率 v， (4)第2秒末的加速度 a 。 解:(1) vx = x/ t = [ x(2)- x(1)]/( 2 - 1 ) = (4.5×22－2×23 )－(4.5－2) = - 0.5 m /s v = - 0.5 i m /s
1-1-2
1-1-2
vx = 9t - 6t2 (4) 加速度 ax = dvx/dt = 9 - 12t |t=2 = 9 - 12×2 = - 15 ( m/s2 ) 因为加速度与速度方向相同， 所以质点在２秒末作加速运动。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
加速度与位移
1．速度和时间的关系
（1）速度公式
由加速度的定义公式a ＝t
v v o t -，可得匀变速直线运动的速度公式为：t v ＝0v +at t v 为末速度，0v 为初速度，a 为加速度．
当a 与0v 3m ／
s ，乙物体在4s 内的平均速度为3m ／s
（2）位移公式
22
1)(212at t v t at v v t v v t v s o o o t o +=++=+== s 为t 时间内的位移．
当a ＝0时，公式为s ＝0v t 当0v ＝0时，公式为s ＝
221at 当a ＜0时，公式为s ＝0v t －22
1at （此时a 只能取绝对值）．
可见：s ＝0v t+2
1a 2t 是匀变速直线运动位移公式的一般表示形式，只要知道运动物体 的初速度0v 和加速度a ，就可以计算出任一段时间内的位移，从而确定任意时刻物体所在的位置．
一、选择题：
1．一物体做匀变速直线运动，下列说法中正确的是（ ）
A ．物体的末速度与时间成正比
B ．物体的位移必与时间的平方成正比
C ．物体速度在一段时间内的变化量与这段时间成正比
D ．匀加速运动，位移和速度随时间增加；匀减速运动，位移和速度随时间减小
2．物体做直线运动时，有关物体加速度，速度的方向及它们的正负值说法正确的是( )
A ．在匀加速直线运动中，物体的加速度的方向与速度方向必定相同
B ．在匀减速直线运动中，物体的速度必定为负值
C ．在直线线运动中，物体的速度变大时，其加速度也可能为负值
D ．只有在确定初速度方向为正方向的条件下，匀加速直线运动中的加速度才为正值
3．物体以2m/s 2的加速度作匀加速直线运动，那么在运动过程中的任意1S 内，物体的( )
A ．末速度是初速度的2倍
B ．末速度比初速度大2m/s
C ．初速度比前一秒的末速度大2m/s
D ．末速度比前一秒的初速度大2m/s
4．原来作匀加速直线运动的物体，若其加速度逐渐减小到零，则物体的运动速度将( )
A ．逐渐减小
B ．保持不变
C ．逐渐增大
D ．先增大后减小
5．汽车以20 m/s 的速度做匀速直线运动，刹车后的加速度大小为5 m/s 2，那么开始刹车6 s 汽车的速度大
小为（ ）
A. 20 m/s
B. 0 m/s
C. —10 m/s
D. 5 m/s
6．关于自由落体运动，下面说法正确的是（ ）
A ．它是竖直向下，v 0=0，a=g 的匀加速直线运动
B ．在开始连续的三个1s 内通过的位移之比是1∶3∶5
C ．在开始连续的三个1s 末的速度大小之比是1∶2∶3
D ．从开始运动起依次下落4.9cm 、9.8cm 、14.7cm ，所经历的时间之比为1∶2∶3
7．甲、乙两车某时刻由同一地点沿同一方向开始做直线运动，若以该时刻作为计时起点，得到两车的x t 图象
如图所示，则下列说法正确的是（ ）
A ．1t 时刻乙车从后面追上甲车
B ．1t 时刻两车相距最远
C ．1t 时刻两车的速度刚好相等
D ．0到1t 时间内，乙车的平均速度小于甲车的平均速度 第7题图
8．在同一地点，甲、乙两个物体沿同一方向作直线运动的速度一时间图象如下图所示，则( )
A．两物体相遇的时间是2S和6S
B．乙物体先在前运动2S，随后作向后运动
C．两个物体相距最远的时刻是4S末，
D．4S后甲在乙前面
9.物体甲的x-t图象和物体乙的v-t图象分别如下图所示
，则这两个物体的运动情况是（）
A．甲在整个t=6s时间内有来回运动，它通过的总位移为零
B．甲在整个t=6s时间内运动方向一直不变，它通过的总位
移大小为4 m
C．乙在整个t=6s时间内有来回运动，它通过的总位移为零
D．乙在整个t=6s时间内运动方向一直不变，它通过的总位移大小为4 m
10.一辆车由甲地出发，沿平直公路开到乙地刚好停止，
其速度图象如图所示，那么0—t和t—3t两段时间
内，下列说法正确的是（）
A加速度大小之比为2: 1
B位移大小之比为1: 2
C平均速度大小之比为1: 2
Ｄ平均速度大小之比为１:１
二、实验题：
11．在“探究小车速度随时间变化的规律”的实验中，打点计时器使用的交流电的频率为50 Hz，记录小车运动的纸带如图所示，在纸带上选择0、1、2、3、4、5的6个计数点，相邻两计数点之间还有四个点未画出，纸带旁并排放着带有最小分度为毫米的刻度尺，零点跟“0”计数点对齐，由图可以读出三个计数点1、3、5跟0点
的距离填入下列表格中.
距离d1d2d3
测量值／cm
计算小车通过计数点“2”的瞬时速度为v2 =______ m/s.
小车的加速度是a =______ m/s2.
三、计算题：
12．汽车在平直的公路上以30m/s的速度匀速行驶，开始刹车以后又以5m/s的加速度做匀减速直线运动，求：
（1）从开始刹车到停下来，汽车又前进了多少米？
（2）从开始刹车计时，第8S末汽车的瞬时速度多大？
13．一物体做匀加速直线运动，初速度为0.5 m/s，第7 s内的位移比第5 s内的位移多4 m，求：
（1）物体的加速度
（2）物体在5 s内的位移
14、火车正以速率v1向前行驶, 司机突然发现正前方同一轨道上距离为s处有另一火车, 正以较小的速率 v2沿同方向做匀速运动, 于是司机立刻使火车做匀减速运动, 要使两列火车不相撞, 加速度a的大小至少应是多少?
15．屋檐上每隔相同的时间间隔滴下一滴水，当第5滴正欲滴下时，第1滴已刚好到达地面，而第3滴与第2滴分别
位于高为1 m的窗户的上、下沿，如图所示，问：
（1）此屋檐离地面多高？
（2）滴水的时间间隔是多少？（g取10 m/s2）
16．一辆卡车初速度v0为10m/s，超车过程的加速度a为2m/s2，求：
（1）卡车在3s末的速度v （2）卡车在6s．．内．的位移x6
（3）卡车在第．6s．．内．的位移xⅥ
17．已知一汽车在平直公路上以速度v0匀速行驶，
（1）司机突然发现在前方x=90m的地方有路障，开始紧急刹车，已知刹车的加速度是a1=-5m/s2，汽车刚好
在路障前面停下，求汽车原来的速度v0是多少？
（2）若汽车的刹车加速度是a2=-3m/s2，初速度不变，为使汽车不撞上路障，司机必须提早多少米发现路障？
18．一火车以2 m/s的初速度，0.5 m/s2的加速度做匀加速直线运动，求：
（1）火车在第3 s末的速度是多少？
（2）在前4 s的平均速度是多少？
（3）在第5 s内的位移是多少？
（4）在第2个4 s内的位移是多少？
19．一辆巡逻车最快能在10 s内由静止加速到最大速度50 m/s，并能保持这个速度匀速行驶，问该巡逻车在平直的高速公路上由静止追上前方2000 m处正以35 m/s的速度匀速行驶的汽车，至少需要多少时间？
20.一辆轿车违章超车，以108 km/h的速度驶入左侧逆行道时，猛然发现正前方80 m处一辆卡车正以72 km/h的速度迎面驶来，两车司机同时刹车，刹车加速度大小都是10 m/s2，两司机的反应时间(即司机发现险情到实施刹车所经历的时间)都是Δt.试问Δt是何数值，才能保证两车不相撞?。