结构的刚度柔度系数
结构动力学基础

m l/ 5
m l/ 5
m l/ 5
m l/ 5
0
1
2
3
4
5
l/5
0
l/5
1y = 1 1 φ1(x) 2
l/5
3
l/5
4
l/5
5
0
2 θ1 = 1 1 φ (x) 2
3
4
5
如图10-9a中,梁分为5个单元,取结点位移参数(挠度y 和转角θ)作为 广义坐标。在图10-9a中取中间四个结点的八个位移参数 y1、θ1,y2、θ2,y3、 θ3,y4、θ4 作广义坐标。
T
sin t
(10 3)
(10 4)
0 -y y T
t
y cos t
v v
y A
0
t
v
sin t
T t
0
A sin t
-A
3、结构的自振周期
由式
A
y (t ) A sin(t ) 及图,可见位移方程是一个周期函数。 2 y T 周 期: T
⑶ 是结构动力特性的重要数量标志。
泛美大厦,60层 钢结构,南北方向 的基本固有周期为 2.90秒,
大坝,400英尺高的混凝土重力坝的基 本固有周期由强迫振动试验测得在蓄水 为310英尺和345英尺十分别为0.288秒 和0.306秒,
金门大桥,金门大桥桥墩跨距1280.2米全桥总 长2737.4米的悬索桥,其横向振动的基本基本固 有周期为18.20秒,竖向振动的基本基本固有周期 为10.90秒,纵向振动的基本基本固有周期为3.81 秒,扭转振动的基本基本固有周期为4.43秒
柔度系数和柔度的关系

柔度系数和柔度的关系全文共四篇示例,供读者参考第一篇示例:柔度系数是材料的一个重要物理性质,它描述了材料的柔软程度。
柔度系数是一个无量纲的值,通常用来比较不同材料之间的柔软程度。
对于某些材料而言,柔度系数是一个非常重要的参数,它直接影响着该材料的使用效果和性能。
柔度系数与材料的柔度直接相关。
柔度是指材料在外力作用下产生的变形程度,通常用来描述材料的柔软程度。
一般来说,柔度系数越大,表示材料越柔软,它可以更容易地被外力变形。
相反,柔度系数越小,表示材料越硬,它不容易被外力变形。
柔度系数与柔度之间存在着密切的关系。
在实际应用中,柔度系数是一个非常重要的物理性质。
在纺织、皮革、橡胶等行业中,柔度系数是评估材料品质的一个重要指标。
在纺织行业中,对于一些衣物材料,柔度系数直接影响着着其舒适度和耐用性。
在皮革行业中,对于皮革材料来说,柔度系数则影响着其触感和弹性。
在橡胶行业中,柔度系数会直接影响到橡胶制品的柔软程度和耐磨性。
不同材料的柔度系数也会受到其结构、成分、制备工艺等多种因素的影响。
在纺织行业中,由于不同纤维的结构和形态不同,它们的柔度系数也会存在一定的差异。
在橡胶行业中,橡胶硬度和弹性也会影响其柔度系数。
要想准确地评估某种材料的柔度,需要综合考虑多种因素。
柔度系数还可以与其他物理性质相互关联。
柔度系数与弹性模量之间存在着一定的关系。
弹性模量描述了材料受到外力作用后的变形程度,它与柔度系数之间存在着一种互补关系。
一个材料的柔度系数越大,其弹性模量往往就越小,反之亦然。
通过研究柔度系数和其他物理性质之间的关系,可以更深入地了解材料的性质和特点。
柔度系数与材料的柔度之间存在着密切的关系。
它是评估材料柔软程度的一个重要参数,在各种行业中都具有重要的应用价值。
通过研究柔度系数和其他相关物理性质之间的关系,可以更深入地了解材料的性质和特点,为材料的设计和应用提供重要的参考依据。
希望本文内容对您有所帮助。
第二篇示例:柔度系数和柔度的关系是材料学中一个重要的概念,它关乎着材料的柔软程度和变形能力。
结构动力学的刚度系数柔度系数汇总.
三、自由振动微分方程的解
y(t ) Asin( t )
四、结构的自振周期和频率
k 1 m m
T
2
五、例题
m
l /2 1 EI l /2
[例1] 计算图示结构的频率和周期。 (柔度法) 解:
1 m
l 48EI
ml 3 T 2 48EI
3
48 EI ml 3
1
k22 k2
k12 k2
k2
EI∞
k11 k1 k2
1
k1
k1 、k2 —— 楼层刚度(本楼层单位侧移所需的侧向力) k11 、k12 、k21 、k22 —— 位移法的刚度系数 kij
kij
—— 第j 个结点位移发生单位位移(其它结点位移均锁固)时, 在第i 个结点位移处产生的反力。
h EI EI
3EI 3EI 6EI k k左柱 k右柱 3 3 3 h h h
总侧移刚度:
h2
h1
i1
i2
k k左柱 k右柱
3 i1 3 i2 2 2 h1 h2
∞ h
总侧移刚度:
i1
i2
12 i1 12 i2 k k左柱 k右柱 2 2 h h
(刚度并联,两者叠加)
k
k11 k
EI
1
l
3EI l3
k11 m
3 EI
l3
k m
[例7]计算图示刚架的频率和周期。
1
m EI1= I I h
k
解: (刚度法)
由柱刚度并联 得:
12 EI 24 EI k 2 3 3 h h
k 24 EI m mh3
结构动力学之多自由度体系的振动问题
2.760 3.342 1
0.163
0.924
2.76
柔度法
利用刚度法的方程间接导出柔度法方程:
由刚度法振幅方程:
令λ=1/ω2 得频率方程:
( [K]-ω2 [M] ){Y}={0}
前乘[K]-1=[δ]后得: ( [I ]-ω2 [δ] [M] ){Y}={0} ( [δ] [M] - λ [I ] ){Y}={0} ┃ [δ] [M] - λ [I ] ┃=0
刚度法
2)如果初始条件是任意的,则任其自然 后, 系统所发生的振动就不是按主振型的简谐自由 振动,而是复杂的周期振动,这时可以用各阶 主振动的线性组合来描述它,也就是说其通解 表为各个特解之和,即
y j sin( j t v j )
j 1 n
所以系统的任意振动可以表示为各个主振动 的叠加。
Yij为正时表示质1 1.293 5Y11 6.70Y21 3 0 量mi的运动方向与单 3Y 1.707 0
21
Y
(1)
0.163 0.569 1
0.569
5Y13 5.027Y23 3 0 (1) Y 3Y21 10.027 0 3.342 1.227
1 1 4 0 , m m 2 9
展开得: 解之:
3 15 2 42 30 0
ξ1=11.601,ξ2=2.246,ξ3=1.151
1 m
三个频率为:
1 0.2936
1 1 3 0.9319 m m 3)求主振型: (令Y3i=1)将λ1代入振型方程: ([δ] [M ]-λ1[I]){Y}=0的前两式:
结构力学问答题总结

概念题1.1结构动力计算与静力计算的主要区别是什么?答:主要区别表现在:(1) 在动力分析中要计入惯性力,静力分析中无惯性力;(2) 在动力分析中,结构的内力、位移等是时间的函数,静力分析中则是不随时间变化的量;(3) 动力分析方法常与荷载类型有关,而静力分析方法一般与荷载类型无关。
1.2什么是动力自由度,确定体系动力自由度的目的是什么?答:确定体系在振动过程中任一时刻体系全部质量位置或变形形态所需要的独立参数的个数,称为体系的动力自由度 (质点处的基本位移未知量)。
确定动力自由度的目的是:(1) 根据自由度的数目确定所需建立的方程个数(运动方程数=自由度数),自由度不同所用的分析方法也不同;(2) 因为结构的动力响应(动力内力和动位移) 与结构的动力特性有密切关系,而动力特性又与质量的可能位置有关。
1.3结构动力自由度与体系几何分析中的自由度有何区别?答:二者的区别是:几何组成分析中的自由度是确定刚体系位置所需独立参数的数目,分析的目的是要确定体系能否发生刚体运动。
结构动力分析自由度是确定结构上各质量位置所需的独立参数数目,分析的目的是要确定结构振动形状。
1.4结构的动力特性一般指什么?答:结构的动力特性是指:频率(周期)、振型和阻尼。
动力特性是结构固有的,这是因为它们是由体系的基本参数(质量、刚度) 所确定的、表征结构动力响应特性的量。
动力特性不同,在振动中的响应特点亦不同。
1.5什么是阻尼、阻尼力,产生阻尼的原因一般有哪些?什么是等效粘滞阻尼?答:振动过程的能量耗散称为阻尼。
产生阻尼的原因主要有:材料的内摩擦、构件间接触面的摩擦、介质的阻力等等。
当然,也包括结构中安装的各种阻尼器、耗能器。
阻尼力是根据所假设的阻尼理论作用于质量上用于代替能量耗散的一种假想力。
粘滞阻尼理论假定阻尼力与质量的速度成比例。
粘滞阻尼理论的优点是便于求解,但其缺点是与往往实际不符,为扬长避短,按能量等效原则将实际的阻尼耗能换算成粘滞阻尼理论的相关参数,这种阻尼假设称为等效粘滞阻尼。
结构力学问答题总结

概念题1.1 结构动力计算与静力计算的主要区别是什么?答:主要区别表现在:(1) 在动力分析中要计入惯性力,静力分析中无惯性力;(2) 在动力分析中,结构的内力、位移等是时间的函数,静力分析中则是不随时间变化的量;(3) 动力分析方法常与荷载类型有关,而静力分析方法普通与荷载类型无关。
1.2 什么是动力自由度,确定体系动力自由度的目的是什么?答:确定体系在振动过程中任一时刻体系全部质量位置或者变形形态所需要的独立参数的个数,称为体系的动力自由度 (质点处的基本位移未知量)。
确定动力自由度的目的是:(1) 根据自由度的数目确定所需建立的方程个数(运动方程数= 自由度数),自由度不同所用的分析方法也不同;(2) 因为结构的动力响应(动力内力和动位移)与结构的动力特性有密切关系,而动力特性又与质量的可能位置有关。
1.3 结构动力自由度与体系几何分析中的自由度有何区别?答:二者的区别是:几何组成份析中的自由度是确定刚体系位置所需独立参数的数目,分析的目的是要确定体系能否发生刚体运动。
结构动力分析自由度是确定结构上各质量位置所需的独立参数数目,分析的目的是要确定结构振动形状。
1.4 结构的动力特性普通指什么?答:结构的动力特性是指:频率(周期)、振型和阻尼。
动力特性是结构固有的,这是因为它们是由体系的基本参数(质量、刚度)所确定的、表征结构动力响应特性的量。
动力特性不同,在振动中的响应特点亦不同。
1.5 什么是阻尼、阻尼力,产生阻尼的原因普通有哪些?什么是等效粘滞阻尼?答:振动过程的能量耗散称为阻尼。
产生阻尼的原因主要有:材料的内磨擦、构件间接触面的磨擦、介质的阻力等等。
固然,也包括结构中安装的各种阻尼器、耗能器。
阻尼力是根据所假设的阻尼理论作用于质量上用于代替能量耗散的一种假想力。
粘滞阻尼理论假定阻尼力与质量的速度成比例。
粘滞阻尼理论的优点是便于求解,但其缺点是与往往实际不符,为扬长避短,按能量等效原则将实际的阻尼耗能换算成粘滞阻尼理论的相关参数,这种阻尼假设称为等效粘滞阻尼。
结构力学问答题总结

概念题1.1 结构动力计算与静力计算的主要区别是什么?答:主要区别表现在:(1) 在动力分析中要计入惯性力,静力分析中无惯性力;(2) 在动力分析中,结构的内力、位移等是时间的函数,静力分析中则是不随时间变化的量;(3) 动力分析方法常与荷载类型有关,而静力分析方法一般与荷载类型无关。
1.2 什么是动力自由度,确定体系动力自由度的目的是什么?答:确定体系在振动过程中任一时刻体系全部质量位置或变形形态所需要的独立参数的个数,称为体系的动力自由度(质点处的基本位移未知量)。
确定动力自由度的目的是:(1) 根据自由度的数目确定所需建立的方程个数(运动方程数=自由度数),自由度不同所用的分析方法也不同;(2) 因为结构的动力响应(动力内力和动位移)与结构的动力特性有密切关系,而动力特性又与质量的可能位置有关。
1.3 结构动力自由度与体系几何分析中的自由度有何区别?答:二者的区别是:几何组成分析中的自由度是确定刚体系位置所需独立参数的数目,分析的目的是要确定体系能否发生刚体运动。
结构动力分析自由度是确定结构上各质量位置所需的独立参数数目,分析的目的是要确定结构振动形状。
1.4 结构的动力特性一般指什么?答:结构的动力特性是指:频率(周期)、振型和阻尼。
动力特性是结构固有的,这是因为它们是由体系的基本参数(质量、刚度)所确定的、表征结构动力响应特性的量。
动力特性不同,在振动中的响应特点亦不同。
1.5 什么是阻尼、阻尼力,产生阻尼的原因一般有哪些?什么是等效粘滞阻尼?答:振动过程的能量耗散称为阻尼。
产生阻尼的原因主要有:材料的内摩擦、构件间接触面的摩擦、介质的阻力等等。
当然,也包括结构中安装的各种阻尼器、耗能器。
阻尼力是根据所假设的阻尼理论作用于质量上用于代替能量耗散的一种假想力。
粘滞阻尼理论假定阻尼力与质量的速度成比例。
粘滞阻尼理论的优点是便于求解,但其缺点是与往往实际不符,为扬长避短,按能量等效原则将实际的阻尼耗能换算成粘滞阻尼理论的相关参数,这种阻尼假设称为等效粘滞阻尼。
两个自由度体系的自由振动.
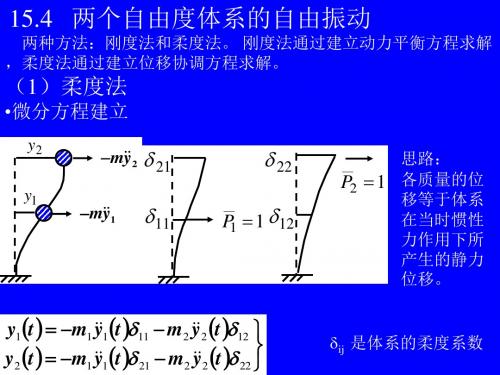
1 1,2 m1 22 m 2 11
Y1 12 m2 1 Y2 11m1 2
22 m2
1
21m1
2
1
1
1
1
Y1 12 m2 (1) 1 Y2 11m1 2
(1)
1
2
2
Y1 12 m2 (2) 1 Y2 11m1 2
2 (1) (2) 2 2
(1)
(2) (2)
m21 Y2 Y2
Y Y
0 称第一正交关系 0 第一主振型惯性力在第二 0 主振型上所做的虚功为零
2 (1) 2
(2)刚度法
•微分方程建立
思路:取质量m1和m2为 隔离体,建立动力平衡方 程。0 m2 y
1 t 11 m2 2 t 12 y1 t m1 y y y2 t m1 y1 t 21 m2 y2 t 22
ij 是体系的柔度系数
设 y1 t Y1sin t y1 t Y1 常数 y t Y 2 y2 t Y2sin t 2 惯性力 惯性力幅值 1 t m1Y1 2sin t m1 2Y1 m1 y 2 2 t m2Y2 sin t m 2 2Y2 m2 y
15.4 两个自由度体系的自由振动
两种方法:刚度法和柔度法。 刚度法通过建立动力平衡方程求解 ,柔度法通过建立位移协调方程求解。
(1)柔度法
•微分方程建立
y2
y1
2 m y 1 m y
21
22
11
P 1 1 12
思路: P2 1 各质量的位 移等于体系 在当时惯性 力作用下所 产生的静力 位移。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k1
、k2 — 楼层刚度
12i2 k2 2 h2
总刚度:
k
P 1 1 1
k1 k2
12i1 k1 2 h1
串联一般公式:
1 1 1 k k1 k2
n 1 1 kn j 1 k j
▲ 楼层刚度与位移法刚度系数的关系
EI∞
k21 k2
6EI k 3 l
1
ky
1 m( y) 2
由∑MA=0 得: y l m( ) my l ky l 0 2 2 化简得: 5my 4ky 0 4k 24 EI 5m 5ml 3
my
(惯性力和弹力)
[例10] 建立图示结构的振动方程,并计算自振频率、周期。
▲ 结构的刚、柔度系数 复习
1. 刚、柔度概念
δ 1
补充内容
柔度 —— 单位力引起的位移。 (力偶) (转角)
1 k
刚度 —— 单位位移所需施加的力。 (转角) (力偶)
两者的互逆关系:
K δ
k 1
1
单自由度时:
● 熟记几种简单情况的刚、柔度
δ 1
悬臂梁自由端: l3 3EI
据此可得:ω1 ׃ω2 ׃ω3= 1 ׃1.512 ׃2
结构约束越强,则刚度越大, 其自振动频率也越大。
[例4] 图示桁架,E=206GPa , A=0.002m2 , mg=40KN , 计算自振频率。( g取10m/s2 )
1
(柔度法) 解:
3
m 4 4
( Fn )i2 li 243 EA 18EA i 1
y
化简得:
A
m
33my 16ky 0
16k 33m
2 2m( y) 5
(惯性力和弹力)
my
[例9]建立图示结构的振动方程,并计算自振频率。
A
m
E1I1=∞
m
EA=∞
A
m
E1I1=∞ k
m
(等效图)
EI l /2 l /2
l
1 y 2
(位移几何关系) A
y
(刚度法) 解:
(2l )3 l3 48EI 6 EI
5
1 87.35 S 1 m
[例5]求图示结构的自振圆频率。
A
h
m
I→∞ EI C
解:先求δ
B
l
1 lh 2h lh 2 EI 2 3 3EI
1
h h
1 3EI 2 m11 mlh
[例6]求图示结构的自振频率。 解:先求k11
k11 m
3EI k11 k 3 l
并联一般公式:
k kj
j 1
n
(2)串联
Δ P h2 k2 Δ1 Δ2
1 1 P 1 P k1
楼面刚度 为无穷大 视同刚臂
1 2 P 2 P k2
h1
k1
1 1 1 1 1 2 P P P k1 k2 k1 k2
(刚度并联,两者叠加)
k
k11 k
EI
1
l
3EI l3
k11 m
3 EI
l3
k m
[例7]计算图示刚架的频率和周期。
1
m EI1= I I h
k
解: (刚度法)
由柱刚度并联 得:
12 EI 24 EI k 2 3 3 h h
k 24 EI m mh3
mh3 T 2 2 EI
1 1 1 1 k k1 k2 k3
3)计算顶端侧移
1 1 1 P P k1 k2 k3 2 2 h3 P h12 h2 24 i1 i2 i3
▲单自由度体系的自由振动要点回顾
一、自由振动 二、振动微分方程的建立
k
3EI l3
i
1 k
两端固支梁侧移刚度: 12 EI 12i k 3 2 l l
i
1
一固一铰支梁的侧移刚度:(同悬臂梁) 1 3EI 3i k 3 2 l l k 简支梁中点柔度、刚度:
l3 48EI 48EI k 3 l
δ
2. 柱的并联、串联刚度 (1)并联 总侧移刚度:
m
EI
k
k
EI
EA=∞ EI l
Δ=1
l
EI l
6i/l
12i/l2
2
48EI k 4 12i / l 3 刚度并联: 解: l 48EI y0 振动方程 my ky 0 即 my 3 l
k 48EI m ml 3
ml 3 T 2 48EI
结 束
(第二版)作业: 10 — 4、5
h EI EI
3EI 3EI 6EI k k左柱 k右柱 3 3 3 h h h
总侧移刚度:
h2
h1
i1
i2
k k左柱 k右柱
3 i1 3 i2 2 2 h1 h2
∞ h
总侧移刚度:
i1
i2
12 i1 12 i2 k k左柱 k右柱 2 2 h h
由图示可知:
k11=k1+k2
k12=k21=-k2
k22=k2
3. 应用举例
P
求图示三层刚架的顶端侧移。
解: 1)计算各楼层(侧移)刚度
i3 i2 i1
i3 i2 i1
12i1 k1 2 2 h1
12i2 k2 2 2 h2
12i3 k3 2 2 h3
(柱并联)
2)计算楼顶点(侧移)柔度
第十三章 结构的动力计算
§13-1 动力计算的特点和动力自由度 §13-2 单自由度体系的自由振动 ▲ 结构的刚、柔度系数复习 §13-3 单自由度体系的强迫振动 §13-4 阻尼对振动的影响 §13-5 两个自由度体系的自由振动 §13-7 两个自由度体系在简谐荷载下的 强迫振动 §13-11 近似法求自振频率
y(t ) Asin( t )
四、结构的自振周期和频率
k 1 m m
T
2
五、例题
m
l /2 1 EI l /2
[例1] 计算图示结构的频率和周期。 (柔度法) 解:
1 m
l3 48 EI
ml 3 T 2 48EI
48 EI ml 3
1
[例2] 计算图示结构的水平和竖向振动频率。
2
[例8]建立图示结构的振动方程,并计算自振频率。
A l /2
2m
EI=∞
m k
l /4
解: (刚度法) 由∑MA=0 得:
l /2
4 y (位移几何关系) 5 4 k ( y) 5 2m
k
2 y 5
2 l 5l 4 2m( y) my k ( y) l 0 5 2 4 5
l/2
l/2
1 ,先求δ 解: m
l3 1 48 EI
l/
2
3l /32 7l5 2 P=1 768 EI
l3 3 192 EI
48 EI 1 ml 3
3 l 768 EI 192 EI 1 l 3 l l 5 l 7 l 2 2 2 (2 3 )3 7 EI 6 2ml 16 2 32 768EI ml 3
(1)ky 0
y 2 y 0
研究作用于被隔离的质量上的力,建立 平衡方程,需要用到刚度系数。 研究结构上质点的位移,建立位移协调方程, 需要用到柔度系数。
超静定结构,查表(形常数)
取决于结构的
刚度系数 柔度系数
谁较容易求得。
静定结构,图乘法求δ
三、自由振动微分方程的解
m
H
1
解:
V
E,I E,A
1 H m H
l3 其中 H 3EI
A,E,I
l
1 V mV
l 其中 v EA
[例3] 图示三根单跨梁,EI为常数,在梁中点有集中质量m , 不考虑梁的质量,试比较三者的自振频率。 m m m
l/2 l/2
3 l/ 16
l/2
l/2
P=1
1
k22 k2
k12 k2
k2
EI∞
k11 k1 k2
1
k1
k1 、k2 —— 楼层刚度(本楼层单位侧移所需的侧向力) k11 、k12 、k21 、k22 —— 位移法的刚度系数 kij
kij
—— 第j 个结点位移发生单位位移(其它结点位移均锁固)时, 在第i 个结点位移处产生的反力。
