浅析几种系综熵的统一表述
信息熵与热力学熵

信息熵与热力学熵信息熵与热力学熵December 2nd, 2011化学及热力学中所指的熵,是一种测量在动力学方面不能做功的能量总数。
熵亦被用于计算一个系统中的失序现象,用来衡量一个系统混乱程度的度量。
热力学熵熵是什么呢?宏观上--体系的熵等于可逆过程吸收或耗散的热量除以它的绝对温度,也就是一种测量在动力学方面不能做功的能量总数。
微观上--熵是大量微观粒子的位置和速度的分布概率的函数,是描述系统中大量微观粒子的无序性的宏观参数。
举例来讲果我们能看到橡皮筋的分子结构,我们会发现它的结构在拉紧和放松的状态时是不一样的。
放松的时候它的分子结构像一团乱麻交织在一起。
而在把橡皮筋拉长的时候,那些如同链状的分子就会沿着拉伸的方向比较整齐地排列起来。
于是我们可以看到两种状态:一种是自然,或者自发的状态。
在这种状态下结构呈混乱或无序状。
而另一种是在外界的拉力下规则地排列起来的状态。
这种无序的状态还可以从分子的扩散中观察到。
用一个密封的箱子,中间放一个隔板。
在隔板的左边空间注入烟。
我们把隔板去掉,左边的烟就会自然(自发)地向右边扩散,最后均匀地占满整个箱体。
这种状态称为无序。
在物理学里我们可以用熵的概念来描述某一种状态自发变化的方向。
比如把有规则排列的状态称为低熵而混乱的状态对应于高熵而熵则是无序性的定量量度。
热力学第二定律的结论是:一个孤立系统的熵永不减少。
换句话说,物质世界的状态总是自发地转变成无序;从低熵变到高熵。
比如,当外力去除之后,整齐排列的分子就会自然地向紊乱的状态转变;而箱子左边的烟一定会自发地向右边扩散。
这就是著名的熵增定律,熵增原理表示自然界会越来越无序。
信息熵那么信息熵是什么呢?一个 X 值域为x1,...,xn的随机变量的熵值 H 定义为:其中,E 代表了期望函数,而 I(X) 是 X 的信息量(又称为信息本体)。
I(X) 本身是个随机变量。
如果p 代表了X 的机率质量函数(probability mass function),则熵的公式可以表示为:信息熵可以认为是系统中所含有的平均信息量大小,也可以认为是描述一个系统需要的最小存储空间长度,即最少用多少个存储空间就可以描述这个系统。
正则系综——精选推荐
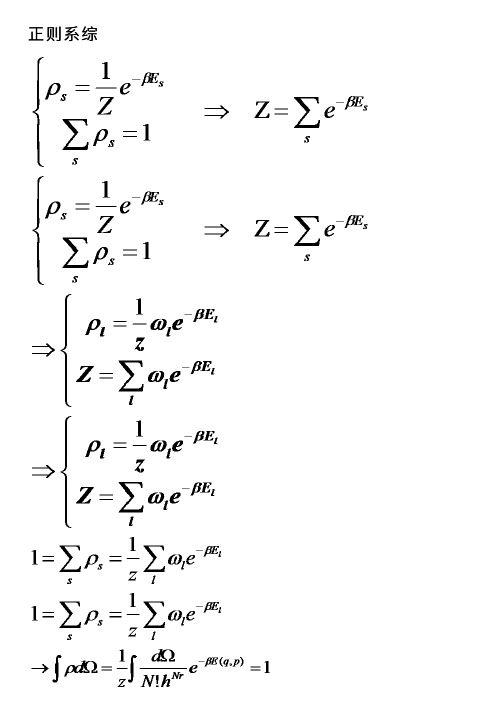
正则系综
1)任意物理量的平均值:物理量A 在⼀切可能的
系统微观状态上的统计平均值2)定义能量涨落:为在⼀切可能
系统微观状态上的统计平均值3)能量相对涨落1、内能(由系综理论:内能U
是在给定N 、V 、T 的
条件下,系统的能量E 在⼀切可能的系统微观状态上
的平均值。
)2、⼴义⼒(系统状态确定在S
时,受⼒为)3、压强
4、熵(已知热⼒学中熵的表达式(闭系))下⾯由统计⼒学中的内能和⼴义⼒的表达式来构造类似的全微分公式。
5、⾃由能
正则系综理论是通过特性函数⾃由能F (N,V,T )来求其他热⼒学函数的能量的涨落适⽤对象:具有确定粒⼦数N,体积V 和温度T
的系统。
分析:具有确定的N,V,T 值的系统可设想为与⼤热源接触⽽达到平衡的系统。
配分函数
1.正则分布的量⼦表达式
2.正则分布的经典表达式正则分布热⼒学函数⼦项⽬
正则系综。
大学物理专题熵

大学物理专题熵在热力学中,熵是一个非常重要的概念。
它被定义为系统无序程度的度量,对于一个封闭系统,熵增加意味着系统从有序向无序演化。
本篇文章将探讨熵在大学物理中的应用。
熵是系统无序程度的度量,它可以通过计算系统所有可能微观状态的概率来定义。
在统计物理学中,熵被定义为:S=k*lnW,其中k是玻尔兹曼常数,W是系统所有可能微观状态的数量。
熵的物理意义在于它表示了系统内部能量的分布。
在一个封闭系统中,当熵增加时,系统内部的能量分布更加均匀,意味着系统的每个部分都具有相同的能量。
因此,当系统达到最大熵时,系统的每个部分都具有相同的温度和压力。
热力学第二定律指出,在一个封闭系统中,熵总是增加的。
这意味着,系统总是朝着能量分布更加均匀的方向演化。
这个定律是热力学的基础之一,它说明了自然界的趋势是朝着更加无序的方向发展。
热力学:在热力学中,熵是一个非常重要的概念。
它被用来描述系统的状态,并且是决定系统是否能够进行热力学的关键因素之一。
统计物理学:在统计物理学中,熵被用来描述系统的微观状态。
它可以帮助我们理解系统的行为和性质。
宇宙学:在宇宙学中,熵被用来描述宇宙的演化。
由于宇宙的演化是朝着更加无序的方向发展,因此熵是描述宇宙演化的一个重要工具。
在大学物理中,熵是一个非常重要的概念。
它被用来描述系统的无序程度和能量的分布。
通过理解熵的概念和应用,我们可以更好地理解自然界的规律和现象。
熵,这个看似简单却意义深远的物理量,无论在科学还是日常生活中都扮演着重要的角色。
然而,许多人可能对其定义和物理意义并不十分了解。
本文将探讨熵的定义和熵的物理意义,以及它在我们生活和工作中的应用。
让我们来看看熵的定义。
在热力学中,熵被定义为系统的混乱度或无序度的度量。
这是一个抽象的概念,但在物理学中,我们通常用它来描述系统中的能量分布或转化。
换句话说,熵描述了系统中的能量是如何被分散或集中,以及这种分散或集中的程度。
从数学角度来看,熵通常被表示为S,其公式为S = k * lnW,其中k为玻尔兹曼常数,W为系统可能的状态数。
熵的定义

热力学第二定律和熵专业:能源与动力工程班级:能源14-3班姓名:王鑫学号:1462162330熵的表述在经典热力学中,可用增量定义为式中T为物质的热力学温度;dQ为熵增过程中加入物质的热量,下标“可逆”表示加热过程所引起的变化过程是可逆的。
若过程是不可逆的,则dS>(dQ/T)不可逆。
单位质量物质的熵称为比熵,记为S。
熵最初是根据热力学第二定律引出的一个反映自发过程不可逆性的物质状态参量。
热力学第二定律是根据大量观察结果总结出来的规律,有下述表述方式:①热量总是从高温物体传到低温物体,不可能作相反的传递而不引起其他的变化;②功可以全部转化为热,但任何热机不能全部地,连续不断地把所接受的热量转变为功(即无法制造第二类永动机);③在孤立系统中,实际发生过程,总使整个系统的熵值增大,此即熵增原理。
摩擦使一部分机械能不可逆地转变为热,使熵增加。
热量dQ由高温(T1)物体传至低温(T2)物体,高温物体的熵减少dS1=dQ/T1,低温物体的熵增加dS2=dQ/T2,把两个物体合起来当成一个系统来看,熵的变化是dS=dS2-dS1>0,即熵是增加的。
熵的相关定义1.比熵:在工程热力学中,单位质量工质的熵,称为比熵。
表达式为δq=Tds,s称为比熵,单位为J/ (kg·K) 或kJ/ (kg·K)。
2.熵流:系统与外界发生热交换,由热量流进流出引起的熵变。
熵流可正可负,视热流方向而定。
3.熵产:纯粹由不可逆因素引起的熵的增加。
熵产永远为正,其大小由过程不可逆性的大小决定,熵产为零时该过程为可逆过程。
熵产是不可逆程度的度量。
熵增原理孤立系统的熵永不自动减少,熵在可逆过程中不变,在不可逆过程中增加。
熵增加原理是热力学第二定律的又一种表述,它比开尔文、克劳修斯表述更为概括地指出了不可逆过程的进行方向;同时,更深刻地指出了热力学第二定律是大量分子无规则运动所具有的统计规律,因此只适用于大量分子构成的系统,不适用于单个分子或少量分子构成的系统实质:熵增原理指出:凡事是孤立系统总熵减小的过程都是不可能发生的,理想可逆的情况也只能实现总熵不变,实际过程都不可逆,所以实际热力过程总是朝着使孤立系统总熵增大的方向进行,dS>0。
关于熵的介绍

熵是一个描述系统无序程度的物理量,它是热力学、信息论和统计物理等领域的重要概念。
熵的概念最早由德国物理学家克劳修斯在1850年提出,源于希腊语,意为“弄清”或“查明”。
熵在物理学中主要用于度量热力学系统的无序程度,而在信息论中,熵是对不确定性的度量。
在热力学中,熵是物质无序度(混乱度)的量度。
在隔离体系(孤立系统)中,自发反应总是朝着熵增加的方向进行。
熵变等于热量微源除以T的积分,其中T为温度。
熵变可以用来判断热力过程是否为可逆过程。
对于可逆过程,熵变为0;对于不可逆过程,熵变大于0。
在化学反应中,反应物和产物都处于标准状态下时,反应过程的熵变称为该反应的标准熵变。
在信息论中,熵是模糊变量不确定性的一种度量。
模糊集用来描述元素无法明确界定是否属于给定集合的集合类,模糊变量则是取值于这种具有不确定性的模糊集的变量。
熵在信息论中的应用主要体现在处理模糊信息,例如在决策树分类中,熵用于度量数据有序还是无序。
熵的概念在物理学、信息论等领域具有重要意义,它有助于我们理解和描述系统的无序程度和不确定性。
静熵和总熵

静熵和总熵
【实用版】
目录
1.静熵和总熵的定义
2.静熵和总熵的关系
3.静熵和总熵的应用
正文
静熵和总熵是热力学中两个重要的概念。
静熵指的是一个系统在静态状态下的熵,也就是系统在没有任何外部干扰下的混乱程度。
总熵则指的是一个系统在任意状态下的熵,包括系统在静态和动态状态下的熵。
静熵和总熵的关系可以用热力学第一定律来描述。
根据热力学第一定律,系统的总熵等于其静熵加上系统所吸收的热量和对外做的功。
这个公式表明了系统的总熵是由其静熵和外部输入的热量和功共同决定的。
静熵和总熵在热力学中有广泛的应用。
例如,在研究热机效率时,我们通常会使用静熵和总熵。
热机效率定义为系统输出的功与系统吸收的热量之比。
通过比较系统的静熵和总熵,我们可以了解热机效率的高低,从而评估热机的性能。
此外,静熵和总熵也可以用于研究热力学循环,如卡诺循环。
卡诺循环是一种理想的热力学循环,它由两个等温过程和两个绝热过程组成。
通过研究卡诺循环的静熵和总熵,我们可以了解热力学循环的效率,并为提高热力学循环的效率提供理论依据。
总之,静熵和总熵是热力学中两个重要的概念,它们描述了系统的混乱程度和热力学过程。
第1页共1页。
两种熵的统一

5 4
第l 2期
N 1 O.2
宜 宾 学 院学 报
Ju a o ii U ie i or l f bn nvrt n Y sy
两种熵 的统 一
柳福提
( 宾 学 院 物 理 与电 子 工 程 系 , 宜 四川 宜 宾 64 O ) 4 O 7
=
收 稿 日期 :0 7— 5—1 20 0 5
作者简介 : 柳福提 (9 8 ) 男, 师, 17 一 , 讲 硕士 , 主要从 事大学物理教学研 究。
维普资讯
20 0 7年 l 2月
柳福提 : 两种墒 的统一
55
无穷小准静 态过程 中, 当外参量有 的改变时 , 外界对系统所 做
行。 对于无限小的过程 , 熵的变化可写为:
d 警 S =
根据克劳修斯所引入的熵, 对于孤立系统( = )任何变 哥 0, 化不可能导致熵的总值减少, S≥0如果变化过程是可逆的, 即d , 则d S=0如果变化过程是不可逆的, d , 则 S>0总之, 。 熵是有增 无减, 即我们称之为熵增加原理。
一 = 一
,
熵是一个极其重要的物理量, 但由于抽象隐晦, 难以理解。 现行大学物理关于熵的定义有两种, 一是在热力学部分介绍克 劳修斯引入的宏观态函数; 另一是玻耳兹曼从微观的角度用统 计的方法得到的微观熵。大多数教材对这两种熵之间的关系讨 论较少, 不利于对熵的认识。本文先分析两种熵的定义, 然后讨 论两者之间的统一关系。 1 克劳修斯熵
文 章 编 号 :6 1 35(07 l 0 5 O 17 —56 2 0 ) 2— 04一 2
统的混乱度就愈大, 即熵是系统混乱度的量度。 不可逆的热力学 变化过程是一个趋向于几率增加的态的变化, 而终态是相应于 最大几率的宏观态, 玻耳兹曼关系式揭示了熵的本质: 熵代表系 统的混乱程度。 下面以经典理想气体为例对玻耳兹曼关系式略 作推导。 假设系统为一封闭系统, 与外界有能量交换但无物质交换, o , l 系统具有确定的粒 热力学第二定律有克劳修斯表述与开尔文表述, 虽然讲的 粒子分布遵循玻耳兹曼分布即 :ce z 分别是热传递和热转变为功两种不可逆过程的方 向和限度, 但 子数Ⅳ温 体 分 必 满 、度 、积 布 须 足Ⅳ=∑o E=∑ , , 他们实际上蕴涵着指出其它一切不可逆过程的共 同规律: 在一 入 分函 数z=∑c -l o  ̄ ̄ l t则U=∑ = ∑ e ee , e 切与热有联系的现象中, 然地实现的过程都是不可逆的。为方 引 配 自 便地判断可逆或不可逆性, 进一步揭示不可逆的本质, 根据热力 学系统所进行的不可逆过程的初态与终态之间有重大差异性, 正是这种差异性决定了过程的方向, 应能找到与不可逆性相关 的态函数。15 年, 84 克劳修斯引进了这一函数称为熵 , S表 用 边积分有: 刁 。
热力学中的熵概念与应用

热力学中的熵概念与应用熵是热力学中一种重要的物理量,它是描述系统无序程度的指标。
在热力学中,熵的概念与应用非常广泛,涉及到热力学定律、热机效率以及自然界中的各种现象等。
熵最初是由德国物理学家鲁道夫·克劳修斯于19世纪提出的。
他认为,在自然界中,所有系统都趋向于无序状态,即系统的熵不断增加。
简单来说,熵可以看作是表征系统混乱程度的一个量。
熵的定义可以通过热力学中的一些基本公式来说明。
根据热力学第二定律,熵的增加总是正的,即系统的熵变大于等于零。
这意味着,在任何热力学过程中,系统的熵总是增加的,而不会减少。
熵的概念在应用中起到了重要的作用。
一个典型的例子是热机效率的计算。
根据热力学第二定律,热机效率只能小于等于某个最大值,这个最大值可以由热机工作温度的比值来确定。
具体来说,热机效率等于1减去冷热源温度的比值。
熵也可以用来解释自然界中一些普遍现象。
比如,自然界中的混合过程总是趋向于增加熵。
当两种物质混合在一起时,原本有序的分子排列就变得无序了,熵增加了。
这也是为什么我们会看到,如果不进行任何干预,咖啡和牛奶会自然混合在一起,而不是分开。
此外,熵的概念还可以用来解释一些生态学中的现象。
例如,生物体的能量流通通常会受到熵增加的限制。
能量通过食物链从一个物种传递到另一个物种,但是每一级能量都会有部分耗散为热能,再也无法利用。
这就意味着,能量的转换效率越高,整个生态系统的熵就越低。
总的来说,熵是热力学中一种重要的物理量,它可以用来描述系统的无序程度。
熵的概念和应用非常广泛,涉及到热力学定律、热机效率以及自然界中的各种现象等。
了解和应用熵的概念,可以帮助我们更好地理解和解释自然界中的各种现象,同时也有助于工程和科学领域的进展。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录摘要 (1)Abstrast (1)1 绪论 (1)2 熵的定义式和熵的可加性 (2)3 各系综体系的熵 (3)3.1 微正则系综的熵 (3)3.2 正则系综的熵 (3)3.3 巨正则系综的熵 (5)3.4 等温等压系综的熵 (6)4 简述信息熵的应用 (8)5 结束语 (8)参考文献 (9)浅析几种系综熵的统一表述摘要:熵是热力学和统计物理中特有的宏观量,它蕴涵着丰富的物理含义,广泛地应用于物质结构、凝聚态物理、低温物理、化学动力学、生命科学和宇宙学以及诸如经济、社会和信息技术等领域。
本文根据微正则系统、正则系统、巨正则系统、等温等压系综的概率分布函数推导出各个系综的熵,并且推导出这几种系综的熵可用熵的定义式表示。
关键词:系综;熵;概率分布函数Analysis of Several Ensemble Entropy Unified DescriptionAbstrast:Entropy is the thermodynamics and statistical physics in the unique macro, it contains a wealth of physical meaning, is widely used in the structure of matter, condensed matter physics, low-temperature physics, chemical kinetics, life science and cosmology, such as economy, society and the information technology field.Based on microcanonical system, regular system, grand canonical system, the isothermal-isobaric ensemble probability distribution function is derived for each ensemble entropy, and deduces the several ensembles of entropy entropy can be used to define type representation.Key words:ensemble;entropy;probability distribution function1 绪论熵是一个极其重要的物理量,克劳修斯于1865年首先引入它,用来定量阐明热力学第二定律。
后来,玻耳兹曼于1872年推导了玻耳兹曼方程式和H定理;于1877年推出了玻耳兹曼关系式,赋予了熵的统计解释,大大丰富了它的物理内涵并明确了它的应用范围。
到1929年,西拉德又发现了熵与信息的关系,揭示了熵的新含义,进一步扩大了熵的应用面。
目前,不仅在自然科学与工程技术的许多领域,甚至在社会科学和人文科学中,熵也有广泛的应用。
本文就由微正则系综、正则系综、巨正则系综和等温等压系综的概率分布函数分别推导出各个系综的熵,并都可用∑-=S SkSρ㏑Sρ来表示。
2熵的定义式和熵的可加性在大多数热学[1]文献中都用熵的玻耳兹曼公式kS=㏑Ω解释其物理意义:孤立系统由非平衡态向平衡态过渡是由熵较小的宏观态向熵较大的宏观态过渡,即由微观态数少的宏观分布向包含微观状态最多的最可几分布过渡。
热力学平衡态是无序程度最大的状态,熵是系统内部微观粒子运动无序程度大小的量度。
以S ρ(S=1,2……)表示为系统处在微观状态S 的概率,S ρ满足归一化条件,即1=∑SS ρ,于是系统的熵定义为[2-4]∑-=SS k S ρ㏑S ρ (1)它作为平衡态熵k S =㏑Ω的推广,也适用于非平衡态,还作为信息熵的定义。
态函数熵是广延量,它的基本属性是可加性。
设系统由两个子系统A 、B 组成,S ρ、A S ρ、BS ρ分别表示处在微观状态S 时的系统,A 子系统,B 子系统的解释,且子系统A 、B 服从统计独立性质,则有S ρ=A S ρ⋅BS ρ 即 ㏑S ρ=㏑A S ρ+㏑B S ρ又A S ρ、B S ρ满足归一化条件:1=∑A A S S ρ,1=∑BB S S ρ 则S ρ也满足归一化条件:1=∑B A S S S ρ则 ∑-=BA S S S k S ρ㏑S ρ()A B A B A B S S S S S S k ρρρρ=-⋅∑㏑ ()A B A B A B S S S S S S k ρρρρ=-∑㏑+㏑ =A A B B B A A B B A S S S S S S S S S S k ρρρρρρ⎛⎫⎛⎫⎛⎫⎛⎫- ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭∑∑∑∑㏑㏑A B S S =+ (2) 以上说明(1)式定义的熵函数满足可加性的要求。
3 各系综体系的熵系综[5]是在一定的宏观条件下,大量性质和结构完全相同的,处于各种运动状态的,各自独立的系综的集合。
系综是统计理论的一种表达方式,是假想的概念,它并不是真实的客观实体,真实的实体是组成系综的一个个系统,这些系统具有完全相同的力学性质。
吉布斯把整个系统作为统计的个体,提出研究大量系统构成的系综在相宇中的分布,克服了气体动理论的困难,建立了统计物理。
在平衡态统计理论中,对于能量和粒子数固定的孤立系统,采用微正则系综;对于可以和大热源交换能量但粒子数固定的系统,采用正则系综;对于可以和大热源交换能量和粒子的系统,采用巨正则系综。
等温等压系综是正则系综的推广,对应于具有恒定温度和压强的体系。
下面就根据学过的理论知识[6,7]推导出熵在这四种系综中的统一表达式。
3.1 微正则系综的熵微正则系综研究的是孤立系统,是由许多具有相同能量,粒子数,体积的体系的集合。
在微正则系综中,概率分布函数为1S ρ==Ω常数,且1=∑S S ρ,并满足等概率原理的基本假设,可推导出微正则系综的熵k S =㏑Ω (3) 且该熵的表达式(3)只适用于微正则系综则 1S S S S S SS S k k k k ρρρρρ=Ω==-=-∑∑㏑㏑㏑㏑ (4) 说明微正则系综的熵可用熵的定义式(1)表示。
3.2 正则系综的熵通常,正则系综内每个体系的粒子数和体积都是相同的。
但每个体系都可以和系综内其他体系交换能量。
同时系综里所有体系的能量之和,以及所有系综的总个数是固定的。
在这些条件下,当系综内所有体系被分配到不同的微观态上,我们发现:每个状态上的体系个数正比于E e β-。
其中1B k Tβ=,B k 是玻耳兹曼常数,T 是绝对温度。
正则系综的配分函数Z 是: S E SZ e β-=∑由于满足归一化条件:1=∑S S ρ则在正则系综中,概率分布函数为:1S E S e Zβρ-= 内能是在给定粒子数N 、体积V 、温度T 的条件下,系统的能量在一切可能的微观状态上的平均值。
因此11S S E E S S SU E E e e Z Z βββ--⎛⎫∂===- ⎪∂⎝⎭∑∑Z β∂=-∂㏑ 由热力学和统计物理知识可得熵的表达式:S k Z Z ββ⎛⎫∂=- ⎪∂⎝⎭㏑㏑ (5) 且该熵的表达式(5)只适用于正则系综。
由统计物理得:S S S U E E ρ==∑,1=∑SS ρ则 S k Z Z ββ⎛⎫∂=- ⎪∂⎝⎭㏑㏑ ()k U Z β=+㏑S S S k E Z βρ⎛⎫=+ ⎪⎝⎭∑㏑()S S S S S k E Z ρβρ⎡⎤=-⋅--⋅⎢⎥⎣⎦∑∑㏑()S S S k E Z ρβ⎡⎤=-⋅--⎢⎥⎣⎦∑㏑ 1SE S S k e Z βρ-⎡⎤⎛⎫=-⋅⋅ ⎪⎢⎥⎝⎭⎣⎦∑㏑ S S Sk ρρ=-∑㏑ (6)说明正则系综的熵能用熵的定义式(1)来表示。
3.3 巨正则系综的熵在巨正则系综中,每个系综内的体系不仅可以和其他体系交换能量,也可以交换粒子,但系综内各体系的能量总和以及粒子数总和都是固定的。
当然系综内的体系总数也是固定不变的,而且各体系的体积是保持在一个固定值上。
巨正则系综对应于具有确定温度T 、确定体积V 和确定化学势μ的体系。
在巨正则系综中,巨配分函数为:s N E Nse αβ--Ξ=∑由于满足归一化条件:1=∑S S ρ则概率分布函数[8]为:1s N E Ns e αβρ--=Ξ由于在系统的各个可能的微观状态中,其粒子数和能量值不是确定的,系统的平均粒子数N 是粒子数N 对给定V 、T 、μ条件下一切可能的微观状态上的平均值:1s N E NsN Ne αβ--=Ξ∑ 1s N E Nse αβα--∂⎛⎫=- ⎪Ξ∂⎝⎭∑1α∂⎛⎫=-Ξ ⎪Ξ∂⎝⎭α∂=-Ξ∂㏑ 内能U 是能量E 的统计平均值:1s N E sNsU E E e αβ--==Ξ∑ 1S N E Nse αββ--⎛⎫∂=- ⎪Ξ∂⎝⎭∑1β⎛⎫∂=-Ξ ⎪Ξ∂⎝⎭β∂=-Ξ∂㏑由热力学和统计物理知识可得熵的表达式:S k αβαβ⎛⎫∂∂=Ξ-Ξ-Ξ ⎪∂∂⎝⎭㏑㏑㏑(7) 且该熵的表达式(7)只适用于巨正则系综。
由统计物理得:s Ns Ns U E E ρ==∑,Ns Ns N N ρ=∑,1Ns Nsρ=∑则 S k αβαβ⎛⎫∂∂=Ξ-Ξ-Ξ ⎪∂∂⎝⎭㏑㏑㏑()k N U αβ=Ξ++㏑Ns s Ns Ns Ns Ns Ns k N E αρβρρ⎛⎫=----Ξ⎪⎝⎭∑∑∑㏑()Ns s Nsk N E ραβ=----Ξ∑㏑1s N E Ns Nsk e αβρ--⎛⎫=-⋅ ⎪Ξ⎝⎭∑㏑ Ns Ns Nsk ρρ=-∑㏑ (8)这说明巨正则系综的熵可用熵的表达式(1)来表示。
3.4 等温等压系综的熵等温等压系综是正则系综的推广,是统计系综的一种。
这个系综对应于具有恒定温度和压强的体系。
每个系综内的体系可以和其他体系进行能量和体积交换。
但系综内各体系的能量总和以及体积总和是固定的,而且各体系有相同的粒子数。
在等温等压系综中,其配分函数为:V E V eγγγβ--∆=∑由于满足归一化条件:1V V γγρ=∑则概率分布函数为[9]:1V E V e γγγβρ--=∆由热力学和统计物理知识可知内能、体积和熵分别为,NU E γβ⎛⎫∂∆==- ⎪∂⎝⎭㏑ ,NV βγ⎛⎫∂∆=- ⎪∂⎝⎭㏑ ,,N N S k γββγβγ⎡⎤⎛⎫⎛⎫∂∆∂∆=∆--⎢⎥ ⎪ ⎪∂∂⎝⎭⎝⎭⎢⎥⎣⎦㏑㏑㏑ (9) 且该熵的表达式(9)只适用于等温等压系综。
由统计物理得:V V U E E γγγρ==∑ V V V V γγρ=∑ 1V V γγρ=∑则 ,,N N S k γββγβγ⎡⎤⎛⎫⎛⎫∂∆∂∆=∆--⎢⎥ ⎪ ⎪∂∂⎝⎭⎝⎭⎢⎥⎣⎦㏑㏑㏑ ()k U V βγ=∆++㏑ V V V V V V k V E γγγγγγγγρβρρ⎛⎫=----∆* ⎪ ⎪⎝⎭∑∑∑㏑ ()V V k V E γγγργβ=----∆∑㏑ 1N E V V k e γγγγβρ--⎛⎫=-⋅ ⎪∆⎝⎭∑㏑ V V V k γγγρρ=-∑㏑ (10) 这说明等温等压系综的熵可用熵的定义式(1)来表示。
