物理分析课程设计---一维扩散方程求解
一维对流扩散方程的格子Boltzmann模型研究

一维对流扩散方程的格子Boltzmann模型研究雷娟霞;李春光【摘要】给出了一维对流扩散方程(e)u/(e)t+α(e)u/(e)x=β(e)2u/(e)x2的一种三速格子Botzmann模型(D1Q3模型).采用Chapman-Enskog多尺度展开技术,导出了该模型的平衡态分布函数.理论分析和数值算例均表明,该模型方法具有计算量小、精度较高等特点.【期刊名称】《宁夏工程技术》【年(卷),期】2018(017)003【总页数】4页(P218-221)【关键词】格子Boltzmann方法;对流扩散方程;Chapman-Enskog展开;平衡态分布函数;数值模拟【作者】雷娟霞;李春光【作者单位】北方民族大学数学与信息科学学院,宁夏银川 750021;北方民族大学数值计算与工程应用研究所,宁夏银川 750021【正文语种】中文【中图分类】O242.1对流扩散方程在数学物理领域扮演着非常重要的角色。
近年来,关于这类方程的一些数值模拟方法逐渐发展起来,包括有限差分法[1—2]、有限元法[3]、有限体积法[4]等。
然而,由于对流扩散方程求解的复杂性,传统的数值模拟方法很难对其进行有效模拟。
格子 Boltzmann 方法(Lattice Boltzmann method,简称LBM)不同于传统的数值方法,它是介于宏观和微观的介观方法。
LBM在求解非线性偏微分方程,特别是在流体力学的研究中取得了很大成果,这是由于LBM具有物理背景清晰、边界容易处理、编程实现简单等优点。
LBM提供了联系宏观和微观的可能性和现实性,除了在一般的流体力学问题中得到了成功的验证之外,在湍流[5—6]、多相流[7]、粒子悬浮流[8]等相关领域也具有广阔的应用前景。
本文利用LBM构造了一个D1Q3模型,该模型具有3个速度方向,平衡态分布函数的最小量也展开到三阶。
本文给出了详细的理论推导,同时用数值算例验证了模型的有效性。
1 模型及方法1.1 一维对流扩散方程考虑如下一维对流扩散方程:式中:α,β为常数为对流项为扩散项。
偏微(08)一阶扩散方程

1 常系数扩散方程 常系数扩散方程
u t
a
2u x 2
,
x
R,
t>
0, (1.1)
a为正常数, 如果给定初始条件
u x,0 g x, x R, (1.2)
(1.1、1.2)就构成了初值问题。
1.1 向前差分格式、向后差分格式
u t
a
2u x 2
,
x
ujn
un-1 j
-a
un j+1
2ujn h2
un j-1
=0 (1.5)
un+1 j
ujn
-a
un j+1
2ujn h2
un j-1
=0 (1.3)
把(1.3)式改写为
隐式
无条件稳定 显式 条件稳定
ujn
un-1 j
-a
un-1 j+1
2ujn-1 h2
un-1 j-1
=0 (1.3) '
2ujn+1
un+1 j-1
un j+1
2ujn
un j-1
=0 (1.8)
一般称为Crank-Nicolson格式
1 时,格式(1.6)为向后差分格式
0 时,格式(1.6)为向前差分格式
1.2 加权隐式格式
0 1 u 2u
t a x2
un j
un-1 j
-a
un j+1
1
1
G ,k的特征方程为
1
1
0
2
2 1
cos
kh
1 1
0 (1.11)
1.3 三层显示格式 引理1.1 实系数二次方程 2 b c 0 的根按其模小于或等于1的充分必要条件是
第五章对流扩散问题(一维稳态对流扩散问题)
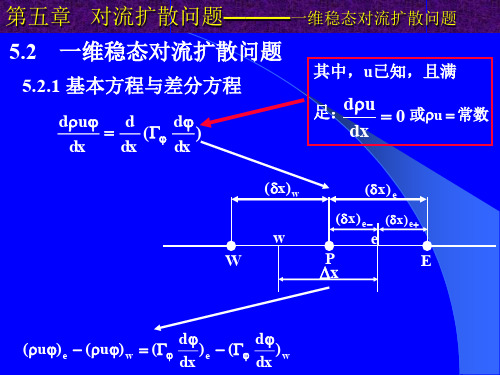
第五章 对流扩散问题———一维稳态对流扩散问题
a P P a E E a W W
中心节点系数
相邻节点系数
aP aE , a W aP aE a W (Fe Fw )
考虑到连续方程
Fe-Fw=0
满足相邻系 数之和准则
a P aE a W
扩散项和以前的处理方法一样,即有:
(u) e e (u) w w e ( E P ) ( x ) e w ( P E ) ( x ) w
而控制容积界面上的变量值取其相应上风侧网格 节点上的值。即:
第五章 对流扩散问题———一维稳态对流扩散问题
第五章 对流扩散问题———一维稳态对流扩散问题 5.2 一维稳态对流扩散问题
5.2.1 基本方程与差分方程
du d d ( ) dx dx dx
(x)w
其中,u已知,且满
d u 足: 0 或u 常数 dx
( x ) e
( x ) e ( x ) e
w W
e P x
a P P a E E a W W
aE 1 4 1 2 4 aW 1 3 2 a P 1 3 4 4 2
2P E 3W
De Dw 1 Fe Fw 4
E 200, W 100
E 100 W 200
2 P 0.25E 1.75 W
De D w 1 Fe Fw 1.5
E 200, W 100
E 100 W 200
P 187.5
P 112.5
某问题 结果合理
第五章 对流扩散问题———一维稳态对流扩散问题
一维扩散方程 自相似解

一维扩散方程自相似解一维扩散方程是描述物质在空间中扩散传播的方程。
它在许多物理和工程领域中都有广泛的应用,例如热传导、扩散过程中的物质浓度变化等。
一维扩散方程的自相似解是指在特定的条件下,方程的解在空间和时间上具有相似性。
先来看一维扩散方程的一般形式:∂u/∂t = D ∂²u/∂x²其中,u(x,t)表示扩散物质在时刻t、位置x处的浓度或温度;D 是扩散系数,反映了传导介质的特性。
对于自相似解,我们希望找到一种特殊的解形式,使得在空间和时间上,解在不同位置和不同时刻具有相似的形态。
为了得到自相似解,我们将引入相似变换。
假设我们有一个自变量变换:x' = x/√(Dt),t' = t/√(Dt),其中D是扩散系数。
通过这个变换,我们可以将原方程变为:∂u/∂t' = ∂²u/∂x'²接下来,我们将应用这个相似变换,来找到一维扩散方程的自相似解。
首先,我们将把扩散方程作为自变量进行变换:u(x,t) = U(x',t')将自变量变换带入一维扩散方程:∂U/∂t' = ∂²U/∂x'²接下来,我们对新的变量x'和t'进行求导,以确定新的依赖关系:∂u/∂x = ∂U/∂x' * ∂x'/∂x + ∂U/∂t' * ∂t'/∂x∂u/∂t = ∂U/∂x' * ∂x'/∂t + ∂U/∂t' * ∂t'/∂t在相似变换中,∂x'/∂x = 1/√(Dt),∂t'/∂x = 0,∂x'/∂t = 0,∂t'/∂t = 1/√(Dt),将这些值带入方程,可得:∂u/∂x = (1/√(Dt)) * ∂U/∂x'∂u/∂t = (1/√(Dt)) * ∂U/∂t'将这些结果代入一维扩散方程,有:(1/√(Dt)) * ∂U/∂t' = (1/√(Dt)) * ∂²U/∂x'²可以发现,新的方程中√(Dt)这一项在两边都能够相互抵消。
一维传热

一维传热扩散方程和求解3.185 2003秋季一维传热扩散方程的k,ρ,(传热系数,密度,比热)对溶质的扩散方程是常数:cp或者在圆柱型坐标:球型坐标1:最重要的不同是在非稳态中使用了热扩散系数pc kρα=,但在傅立叶第一定律中使用了热传导系数k 来计算热通量:基于以上原因,把D 用k 和α来代替,并使p c ρ等于1,就可以得到溶质扩散方程。
1许多书上都简化了圆柱和球形方程,分别被r 和r 除,并使含有r 的项分离出来,就得到2圆柱型p c q r T r r T t Tρα&+∂∂+∂∂=∂∂)122(球型p c q r T r r T t T ρα&+∂∂+∂∂=∂∂)222(一维热传导答案1. 稳态(a)无热量产生i 笛卡尔方程:答案:T=Ax+B通过平板的传导通量大小和通过流体边界层的热传导(和一级化学反应或者通过流体边界层的质量传递相似):(是流体温度,和扩散中的流体浓度相似;是流体反方向的温度) fl T 1T 无量纲形式:其中khLh =π(a.k.a毕渥数) ⅱ圆柱型方程答案T=A㏑r+B结合在通过流体边界层的热量传热和在,之间的通过柱体的传导的通量大小1R 1R 2Rⅲ球坐标方程答案T=A/r+B(b)产生恒定的热量¡笛卡尔方程答案ⅱ圆柱坐标方程答案ⅲ球坐标方程答案(c)(只有扩散)一级均向反应消耗反应物,所以G=-Kc ⅰ笛卡尔方程答案ⅱ包含贝塞尔函数的圆柱和球坐标答案,但方程式如下:2建立在笛卡尔坐标上没有热量产生,具有恒定的k,p c ρ的非稳态答案其中pc k ρα=(a )相同的起始条件T=,恒定的边界条件x=0,∞T S T T =半无限厚介质;或者无限厚介质的起始条件是阶越函数。
答案是试差函数或者它的补集半无限厚介质标准注释:这种理论也可以用于“组合扩散”,就是两个不同温度(浓度)的物体在x=0连接在一起,并彼此扩散;边界条件是两个物体边界条件的中间值。
物理分析课程设计---一维扩散方程求解

课程设计报告课程名称:核反应堆物理分析题目:一维扩散方程求解院系:核科学与工程学院班级:学号:姓名:指导教师:成绩:教师签名:日期:2011 年6月日目录摘要 (1)课程设计的目的与要求 (1)设计正文 (1)课程设计总结或结论 (3)参考文献 (4)摘要和关键词摘要这个设计用微分方程的差分数值求解方法,运用MATLAB编程计算出一维扩散方程中子通量密度的离散解。
关键词:一维扩散方程一.课程设计的目的与要求学习使用微分方程的数值解法(差分方法)来近似求解一维扩散方程,掌握差分方法的核心思想,熟练使用matlab数据处理,origin绘图软件。
通过给定的微分方程及边界条件,计算平板型,圆柱形,球形反应堆中子通量密度分布。
二.设计正文通过查找有关资料,根据二阶线性微分方程○1转换为差分方程的一般公式其中○2h为给定步长,我们把原方程化简为○3对比方程○1和○3得出○4把○4代入○2等式右端向量差分方程其实就是一个线性方程组,此线性方程组的系数矩阵为:则有这是一个三对角阵,故可用追赶法解式○3。
下面通过matlab程序来计算变换后的差分方程的解。
所编程序如下:clear;N=input('请输入参数:');alpha=input('请输入alpha值:');if alpha==0rmax=input('请输入平板的厚度:');f0=input('请输入平板中心的中子通量密度:');elseif alpha==1rmax=input('请输入堆芯半径:');f0=input('请输入圆柱中心的中子通量密度:');elseif alpha==2rmax=input('请输入堆芯半径:');f0=input('请输入球形中心的中子通量密度:');endh=rmax/N;D=0.8*10^(-2)for i=1:1:N-1a(1,i)=2*D*(i-1/2)^alpha*h^(alpha-1);c(1,i)=2*D*(i+1/2)^alpha*h^(alpha-1);b(1,i)=a(1,i)+c(1,i)+2*h*8.5*10^(-28)*(i*h)^2;g(1,i)=2*i^2*h^3*10^14*cos(pi*i*h/2);endnewa=a(:,2:N-1);newc=c(:,1:N-2);Hb=diag(b);Hc=diag(newc,1);Ha=diag(newa,-1);H=-Ha+Hb-Hc;G=g;G(1,1)=g(1,1)+a(1,1)*f0;p(1,1)=b(1,1);for k=1:1:N-2q(1,k)=c(1,k)/p(1,k);p(1,k+1)=b(1,k+1)-a(1,k+1)*q(1,k);endfor k=1:1:N-2y(1,1)=G(1,1)/p(1,1);y(1,k+1)=(G(1,k+1)-a(1,k+1)*y(1,k))/p(1,k+1);endfor k=N-2:-1:1u(1,N)=y(1,N-1);u(1,k+1)=y(1,k)-q(1,k)*u(1,k+2);endu(1,1)=f0;u(1,N+1)=0;X=0:h:rmax;P=polyfit(X,u,5)U=polyval(P,X);plot(X,U)三.课程设计总结或结论本次课程设计加深了我对中子扩散理论的认识,充分的将理论和实践结合起来。
一维热扩散问题的c++描述

标题:一维热扩散问题的C++描述一维热扩散问题在物理学和工程领域中具有重要的应用。
它描述了热量在一维空间中的传导和扩散过程,是热传导方程的一个经典问题。
在本文中,我们将使用C++编程语言来描述一维热扩散问题,并计算其数值解。
本文将从问题的数学描述开始,然后逐步介绍如何用C++来模拟热传导过程,并给出完整的代码和计算结果。
问题描述:1. 数学模型假设我们有一个长度为L的均匀材料棒,初始时刻材料棒的温度分布为u(x,0)。
根据热传导方程,材料棒上任意一点x处的温度u(x,t)满足如下偏微分方程:∂u/∂t = α ∂²u/∂x²其中α是材料的热扩散系数。
我们假设材料棒的两端保持在恒定的温度,即u(0,t)=u0,u(L,t)=uL。
这就构成了一维热扩散问题的数学模型。
2. 离散化方法为了求解这个偏微分方程,我们需要对空间和时间进行离散化。
我们将材料棒均匀地划分成N个小段,长度为Δx,时间上也划分成M个小段,长度为Δt。
对于任意的i和j,我们用u(i,j)来表示材料棒上第i 个小段的温度在第j个时间点的值。
C++代码实现:1. 初始化参数我们需要初始化材料棒的参数,包括长度L、离散化的段数N、时间步长Δt等。
```cppdouble L = 1.0; // 材料棒长度int N = 100; // 离散化的段数double dx = L / N; // 空间步长double dt = 0.001; // 时间步长double alpha = 0.1; // 热扩散系数```2. 初始化温度分布接下来,我们需要初始化材料棒的温度分布,即u(x,0)。
我们可以假设初始时刻的温度分布为一个正弦波或者矩形波等。
```cppdouble u0 = 0.0; // 棒的左端温度double uL = 1.0; // 棒的右端温度std::vector<double> u(N+1,0.0); // 温度数组for(int i=0; i<=N; i++){u[i] = 0.5*sin(2*3.1415*i/N); // 正弦波初始温度分布}```3. 迭代求解我们使用显式差分格式来迭代求解热传导方程。
第五章对流扩散问题(一维稳态对流扩散问题)

第五章 对流扩散问题———一维稳态对流扩散问题
对控制方程在P点的控制容积积分后,得到如下方程
(u ) e (u ) w ( d d ) e ( )e dx dx
第五章 对流扩散问题———一维稳态对流扩散问题
所以,当 F 2D,即意味着两节点对其间变量分布 的影响特性是受扩散控制的,当 F 2D时,即意味 着两节点对其间变量分布的影响特性是受对流控 制的。对于前者,两节点之间的变量分布偏离线 性分布,但尚不显著,而对于后者两节点之间的 变量分布则严重偏离线性分布。
P<<-1
P=-1
P=0
P=1 P>>1
0
0 L/2 L
第五章 对流扩散问题———一维稳态对流扩散问题
说明
由图很容易看出,只有在贝克列数为零的极限条 件下,即对纯扩散问题或导热问题,变量在任意 两点之间的变化才是线性的。即在没有流动的情 况下,我们假定变量在任意两个节点之间的线性 分布才是可以接受的。 当贝克列数不为零时,即存在对流过程时,变量 在任意两点之间的变化是偏离线性的。贝克列数 的绝对值越大,这种偏离越严重。所以我们在用 控制容积法推导差分方程时,假定任意两个节点 之间变量呈线性变化显然是有问题的。
e P e E
如果 Fe 0 如果 Fe
0
同样
w W
w P
如果 Fw 0
如果 Fw 0
为了能写出差分方程,我们定义一个新的算子,如下:
A, B AMAX( A, B)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程设计报告
课程名称:核反应堆物理分析题目:一维扩散方程求解院系:核科学与工程学院班级:
学号:
姓名:
指导教师:
成绩:
教师签名:
日期:2011 年6月日
目录
摘要 (1)
课程设计的目的与要求 (1)
设计正文 (1)
课程设计总结或结论 (3)
参考文献 (4)
摘要和关键词
摘要
这个设计用微分方程的差分数值求解方法,运用MATLAB编程计算出一维扩散方程中子通量密度的离散解。
关键词:一维扩散方程
一.课程设计的目的与要求
学习使用微分方程的数值解法(差分方法)来近似求解一维扩散方程,掌握差分方法的核心思想,熟练使用matlab数据处理,origin绘图软件。
通过给定的微分方程及边界条件,计算平板型,圆柱形,球形反应堆中子通量密度分布。
二.设计正文
通过查找有关资料,根据二阶线性微分方程
○1
转换为差分方程的一般公式
其中
○2
h为给定步长,
我们把原方程化简为○3
对比方程○1和○3得出
○4
把○4代入○2
等式右端向量
差分方程其实就是一个线性方程组,此线性方程组的系数矩阵为:则有
这是一个三对角阵,故可用追赶法解式○3。
下面通过matlab程序来计算变换后的差分方程的解。
所编程序如下:
clear;
N=input('请输入参数:');
alpha=input('请输入alpha值:');
if alpha==0
rmax=input('请输入平板的厚度:');
f0=input('请输入平板中心的中子通量密度:');
elseif alpha==1
rmax=input('请输入堆芯半径:');
f0=input('请输入圆柱中心的中子通量密度:');
elseif alpha==2
rmax=input('请输入堆芯半径:');
f0=input('请输入球形中心的中子通量密度:');
end
h=rmax/N;
D=0.8*10^(-2)
for i=1:1:N-1
a(1,i)=2*D*(i-1/2)^alpha*h^(alpha-1);
c(1,i)=2*D*(i+1/2)^alpha*h^(alpha-1);
b(1,i)=a(1,i)+c(1,i)+2*h*8.5*10^(-28)*(i*h)^2;
g(1,i)=2*i^2*h^3*10^14*cos(pi*i*h/2);
end
newa=a(:,2:N-1);
newc=c(:,1:N-2);
Hb=diag(b);
Hc=diag(newc,1);
Ha=diag(newa,-1);
H=-Ha+Hb-Hc;
G=g;
G(1,1)=g(1,1)+a(1,1)*f0;
p(1,1)=b(1,1);
for k=1:1:N-2
q(1,k)=c(1,k)/p(1,k);
p(1,k+1)=b(1,k+1)-a(1,k+1)*q(1,k);
end
for k=1:1:N-2
y(1,1)=G(1,1)/p(1,1);
y(1,k+1)=(G(1,k+1)-a(1,k+1)*y(1,k))/p(1,k+1);
end
for k=N-2:-1:1
u(1,N)=y(1,N-1);
u(1,k+1)=y(1,k)-q(1,k)*u(1,k+2);
end
u(1,1)=f0;
u(1,N+1)=0;
X=0:h:rmax;
P=polyfit(X,u,5)
U=polyval(P,X);
plot(X,U)
三.课程设计总结或结论
本次课程设计加深了我对中子扩散理论的认识,充分的将理论和实践结合起来。
基本了解源迭代,中子通量密度迭代的方法,充分认识到有限差分法在扩散临界计算中的重要性。
四.参考文献
微分方程数值方法(第二版)胡建伟汤怀民编MATLAB程序设计与应用(第二版)刘卫国主编
核反应堆物理分析谢仲生等编
附录(设计流程图、程序、表格、数据等)
真实的离散数据
5次多项式拟合所得图形
在求解区间[a,b]按N等分划分微分方程在网点
用差商代替倒数,
省略高阶无穷项
用追赶法求解对
三角阵
用matlab做拟合
曲线。
