水文随机分析径流量预测
河流径流量预测与相互关系分析

问题要求利用附件中的已知数据,根据各水文站的日平均水位、降水量数据预测未来3天的径流量。为了合理利用数据简化处,本文首先选择12月的日水位和降水量数据作为参考数列,建立灰色预测模型,预测出该年12月份的日平均水位和降水量值;然后将预测结果与实际值作比较,计算得预测值与实际值的相对误差,在误差范围允许的情况下,再利用灰色预测法得到未来3天的日平均水位和降水量值。最后,我们将所预测得的日平均水位和降水量数据代入所建立的数学模型,由Matlab软件计算得到未来3天的径流量值。
2.3对问题三的分析
此题要求在此流域设置二个大型水库,用于平衡调节各地区径流量及抗旱蓄水,请问如何设置此水库位置,并分析原因。地区是否缺水或者水量是否过多,主要的判断条件就是供水量和用水量之间的大小关系,如果供水量小于用水量将会发生缺水的情况,反之,则会有水涝的可能。本文在这一基础上,对不同地区不同月份的用水、供水量进行讨论,从而分析出各个地区旱涝情况,再根据这个情况,结合河道上下游之间的相互影响,选择水库的建设位置。
针对问题一,首先根据平均水位和降水量与径流量的趋势图判定相互之间的关系,再根据这种关系确定回归方程的函数形式并进行回归分析,建立回归方程,确定平均水位和降水量与径流量的数量关系。然后运用灰色预测法分别对各水文站的平均水位和降水量进行定量的预测,最后结合所建立的回归模型以及平均水位与降水量的灰色预测值对未来三天的河流径流量进行预,预测结果见表1。
2.2对问题二的分析
此题要求分析各个控制断面间径流量相互制约关系,由河流水文站网络概化图可知,每一个水文站的径流量与其上游水文站的径流量以及周围用水消耗量等因素有关,且各水文站之间相互影响、相互制约。为了简化问题,我们可以从众多的控制断面中选取一些位于排污区(口)下游和流经特殊要求地区(如饮用水源地、风景游览区等)的河段上等较为关键的控制断面作为研究对象,然后分别考虑这些控制断面间径流量的相互制约关系。
汤旺河流域主要测站年径流量随机性与趋势性分析
21 00年 第 l 期 ( 3 第 8卷)
黑 龙 江 水 利 科 技 H in jn c n eadT cnlg f t osrac e og agSi c n ehooyo e C nevn y l i e Wa r
No . .1 201 0
( oa N . 8 T dl o3 )
此检验也 称 一检 验 , 以连 续观 测 值超 过某 特 定值 的个数 r 是 ( 记为 P 的 一种榆验 。例如 , ) 某水文要素系列 X , 2… , , X , 假定 它是连续增加 的( 升趋势 ) 那么 , , 先以 , 比较特定 为
参 考文 献 :
[ ] 金光炎 . 1 随机水资源技术 [ . M] 北京 : 出版社 , 8 . 农业 1 7 9 [ ] 金光炎 . 2 水文统计原理与方法[ . M] 北京: 中国工业出版社 , 6. 14 9
[ 收稿 日期]0 9—1 6 20 2—1 [ 作者简 介] 肖鹏云( 92一) 男, 16 , 黑龙 江勃利人 , 工程师 ; 李敬 东( 9 3一) 女 , 16 , 黑龙 江依 兰人 , 师 ; 技 田长涛(9 9一) 男, 16 , 黑 龙江伊春人 , 工程师 。
----— —
4 .— 4 - - - —
5 的显 著 性 水 平 下 不 能 拒 绝 。至 于 五 营 、 明 没 有 通 过 趋 % 晨 势检验 的测站 , 由 P是否接近 ( 可 n一1 )×0 2或 0两种极 端 . / 情况来做进一步检验 判断 。五营 站 n= 9 P=( 4, n一1 )× n 2=17 , 3中实际 P=35 / 16 表 8 。晨明站 n 3 P=( 一1 =5 , n )× n2:17 , 3中实际 P= 2 。 两站 的实际 P 既不接近 ( / 38表 51 , n I n 2 也不 接近 0这两种 极端 情况 。说 明其 上升或 下 )× / , 降趋势不十分明显 , 仍可将其划归于无明显趋势之列。 表 2 资料随实际工作 中, 了进 一步 分析 、 测某 一水 文要 素的 为 预 变化规律 , 经常会 建 立 一些 水 文数 据分 析 、 拟数 学 模 型。 模 在根据随机水文学原 理和 分析技术 对水文 要素 系列 数据建 立分析模型时 , 了了解资料系列有无 明显的 系统 性影 响和 为 趋势性的存在 , 要对数据系列进行必要 的随机性 和趋势性 检 验, 然后才能建立数据分析模型 。本文 以汤旺河 流域控制 面 积较大的 5个主要测站 为例来 分析各 站年 径流 量数 据 的随 机性和趋势性特征 , 各站资料系列 情况见表 1 。 表 1 选 用测 站一览表
水文随机分析第一二章110914

2018/10/24
水文水资源学院
17 17
当n=2时, F ( x1 , x2 ; t1 , t 2 ) F ( x1 k , x2 k ; t1 k , t 2 k ), t2 t1 ,
2008年,王文圣,丁晶, 随机水文学,”十一五”规划教材,水利出版社 2009年,丛树铮,水科学中的概率统计方法,科学出版社 2011年 黄振平,陈元芳,水文统计学,中国水利水电出版社
2018/10/24 水文水资源学院 6
(五)考核方法
笔试(开卷,30%),主要涉及课堂教学内容,有一定难度, 平时加上撰写小论文(40%),面试(30%,?)。
Qm 序列或时间序列,如年最大 等,如 t为连续的则仍称随机过程。
在给定t情况下, 就是一个随机变量,其取值可以是离散的,
也可以是连续的。(水文上一般是连续型的,年径流量 、年最 (t )
高水位等;也有离散的,如年降水天数,1,2,…,365)Qm
2018/10/24
水文水资源学院
11
随机过程的分类
南京气温值还随空间位置不同而变化。换句话说,参变量不
一定总是时间,可以是其他。这些随机变量即为随机函数。 特别是:我们常称以时间t为参变量的随机函数为随机过程。 当然如果涉及水文现象的随机过程则称为水文随机过程,一 般用 表示。
( t )
2018/10/24 水文水资源学院 10
t可以是连续的,也可以是离散的。如t为离散的则简称随机
2018/10/24 水文水资源学院 2
随机方法在水文学的应用
随机方法在水文学中的应用一、概述水文现象随时间变化的过程称为水文过程或水文序列,水文现象是一种自然现象,具有确定性变化规律和随机性变化规律。
这些确定性和随机性的变化规律通过水文过程可以较为清晰的展示出来。
水文过程中的确定性变化规律突出表现在过程中有年、日的变化。
如日、旬、月径流过程,明显存在以年为周期的变化;逐时气温和蒸发量过程存在一日为周期的变化。
这是由于影响水文过程的确定性因素——气候因素存在以年为周期的变化和某些气象因素存在以日为周期的变化之故。
水文过程在表现出确定性变化规律的同时,更多的表现出随机性变化特征。
如每一年的的月平均流量过程不相同,形状和数量相差较大;水文过程内前后期要素之间好似变化无序,时大时小,但它们之间存在相依关系,2月平均流量与1月平均流量相依,后一年与前一年径流量相依。
随机性变化特征是水文过程形成与演变中众多影响因素所致。
这些影响的无限复杂性和多样性,致使水文过程不断发生着各种各样情形,表现出随机变化特征。
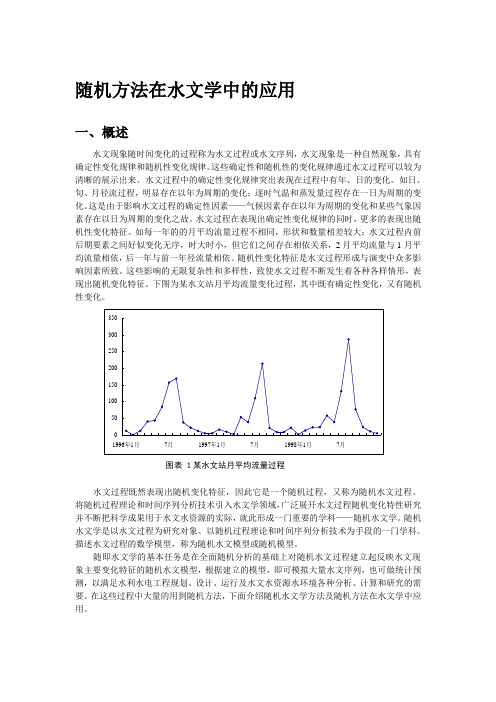
下图为某水文站月平均流量变化过程,其中既有确定性变化,又有随机性变化。
350300250200150100501996年1月7月1997年1月7月1998年1月7月图表1某水文站月平均流量过程水文过程既然表现出随机变化特征,因此它是一个随机过程,又称为随机水文过程。
将随机过程理论和时间序列分析技术引入水文学领域,广泛展开水文过程随机变化特性研究并不断把科学成果用于水文水资源的实际,就此形成一门重要的学科——随机水文学。
随机水文学是以水文过程为研究对象、以随机过程理论和时间序列分析技术为手段的一门学科。
描述水文过程的数学模型,称为随机水文模型或随机模型。
随即水文学的基本任务是在全面随机分析的基础上对随机水文过程建立起反映水文现象主要变化特征的随机水文模型,根据建立的模型,即可模拟大量水文序列,也可做统计预测,以满足水利水电工程规划、设计、运行及水文水资源水环境各种分析、计算和研究的需要。
径流量估算综合论述PPT课件( 22页)

第二阶段 大发展阶段
随着计算机技术的进步和流域产汇 流理论的初步建立七八十年代流域 水文模型取得重大突破,一些比较 著名的模型如美国Stanford模型、 日本的水箱模型、欧洲的SHE模型以 及我国的新安江模型都形成于这一 时期。
那我们怎样估算径流量?
比如,已知某一地区的自然地理要素的性 质,以及观测到的一些资料,有的时候面 对缺乏观测资料的地区,我们怎样来计算 河流的径流量呢?这个问题人类已经探索了 几千年了,但近代之前我们得到的径流量 知识都是定性的。近代科学兴起后,人们 开始对径流量形成的某一环节进行定量计 算。直到上世纪五十年代,水文工作者才 运用系统的观点提出流域水文模型概念, 这之后,流域水文模型就成了计算径流量 的一个有力工具。
河 流 蓄 水
流域 出流
欢迎大家批评指正! 谢谢大家!
•
5、世上最美好的事是:我已经长大,父母还未老;我有能力报答,父母仍然健康。
•
6、没什么可怕的,大家都一样,在试探中不断前行。
•
7、时间就像一张网,你撒在哪里,你的收获就在哪里。纽扣第一颗就扣错了,可你扣到最后一颗才发现。有些事一开始就是错的,可只有到最后才不得不承认。
二、什么是水文模型呢?
水文模型就是用数学语言或物理 模型对现实水文系统进行刻划或 比拟,并在一定的条件下对水文变 量的变化进行模拟和预报。建立 水文模型的目的就是能够对一个 水文系统的未来变化进行预报。 流域水文模型很显然就是基于某 一河流流域而建立的水文模型。
流域水文模型简史
第一阶段 起步阶段 始于20世纪50年代,在这之前水
云
水文测绘技术中的水流模拟和预测方法

水文测绘技术中的水流模拟和预测方法水文测绘是一项关键的技术,旨在研究和测量水域的水文参数,以便更好地了解水文系统的动态。
在水文测绘中,水流模拟和预测是其中一项重要的任务。
本文将介绍水文测绘技术中的水流模拟和预测方法,以及其在科学研究和实际应用中的重要性和挑战。
一、水流模拟方法1. 物理模型物理模型是水流模拟中最常用的方法之一。
它基于物理原理和方程式,通过实验室试验或现场测量来模拟和预测水流的行为。
物理模型可以使用小尺度的实验设备或基于真实地理环境的大型试验平台。
例如,为了模拟河流的水流行为,可以使用一条小型的河流模型,通过在模型中注入水流,并观察水流的速度、流量和方式等指标,来预测实际河流的水流行为。
物理模型能够提供客观准确的实验数据,但也面临着试验成本高昂、实验周期长等问题。
2. 数学模型数学模型是水流模拟的另一种常用方法。
它利用数学工具,将水流系统的物理过程抽象为数学方程组,并通过求解方程组来模拟和预测水流的行为。
常见的水流数学模型包括水流动力学模型、水文模型和水质模型等。
水流动力学模型主要研究水流的运动规律,通过求解牛顿第二定律等方程,预测水流速度和流量等参数。
水文模型用于预测降雨径流过程,通过模拟降雨入渗和径流形成的过程,提供洪水预警和水资源管理的决策支持。
水质模型则用于模拟水体中污染物的扩散和传输过程,帮助评估水体水质状况和污染控制措施的效果。
数学模型在水流模拟中具有灵活性和高效性的优势,但也需要准确的参数输入和较长的计算时间,对模型建立和精确性要求较高。
二、水流预测方法水文测绘技术中的水流预测是基于历史数据、观测数据和模型推演等手段,对未来特定时间段的水流进行预测和估计。
1. 统计模型统计模型是常见的水流预测方法之一。
它通过对历史数据中的水文特征进行统计分析和建模,建立数学方程,从而预测未来水流。
常用的统计方法包括回归分析、时间序列分析和灰色系统分析等。
例如,在预测下一年的降雨径流过程时,可以通过回归分析找到降雨量和径流量之间的关系,进而预测未来的径流量。
基于SARIMA模型的月径流量预测

基于SARIMA模型的月径流量预测作者:贺依韬马腾来源:《科技资讯》2020年第06期摘; 要:径流量预测是水文学研究的重要方向之一,开展径流预测,对于区域水资源的综合开发利用、合理配置、高效管理具有重要的指导作用。
径流序列可以视为典型的时间序列,SARIMA模型是一种常用的时间序列模型,能够间接考虑其他相关随机变量的变化,建模高效、便捷。
该文在某水文站30年历史月径流量分析的基础上,建立SARIMA模型对该水文站未来18个月的径流量进行预测,预测结果的确定性系数为0.8594,预测精度较高,对于该区域的水文工作的开展具有重要的现实意义。
关键词:径流预测; 时间序列; SARIMA模型; 模型评价中图分类号:TV214 ; ;文献标识码:A 文章编号:1672-3791(2020)02(c)-0042-03数据驱动模型不以水文过程作为模型建立的基础,而是着重于数据关系的分析,建模方便高效,预测精度高。
常见的数据驱动模型有多元回归分析、时间序列分析、神经网络等。
其中多元回归分析预报因子选择困难,对预测精度影响较大,神经网络需要数据量大,预测结果不稳定。
时间序列模型通过少量数据就可做出精确的短期预测,因而被广泛应用,其中SARIMA 模型是一种考虑到序列周期变化的时间序列建模方法。
某一观测或统计数值按其发生的时间先后顺序形成的数列称为时间序列[1]。
水文观测值按期观测时间形成的数列是一种典型的时间序列[2]。
该文在水文时间序列分析的基础上建立SARIMA模型对某水文站历史月径流量进行拟合,选择最优模型对未来一段时间的月径流量进行预测,以期为该地区水文工作提供参考。
1; 研究方法对于平稳时间序列[4],一般可对其建立自回归滑动平均ARMA(p,q)模型,它是自回归AR(p)模型和移动平均MA(q)模型的组合,其模型的基本形式如式(1)。
yt=c+1yt-1+2yt-2+...+pyt-p+et+θ1et-1+θ2et-2+…+θqet-p; ; (1)式(1)中,yt为时间序列第t时刻的观察值;yt-1,yt-2,…,yt-p为时序yt的滞后序列;et,et-1,et-2,…,et-q为模型在第t期,第t-1期,…,第t-q期的误差;1,2,…,p,θ1,θ2,…,θq为待估计参数;c为常数项。
径流随机模拟

径流随机模拟由于实际水文资料往往比较短,难于满足实际水文程作随机模拟。
这种随机模拟的目的之一在于充分利用是用来延长资料长度。
当所建模型及参数准确时,这种年月径流随机模拟方法,对于多站及更深入的随机模拟一、随机过程基本知识(一)随机过程和时间序列的定义在实际问题中,常涉及试验过程随某个参变量的变的流量、水位是随时间变化的随机变量,气温是随时间这种随机变量为随机函数,并称以时间为参数的随机函数为随机过程,记为}),({T t t ∈ξ,T 是t 变化的范围。
随机过程在一次试验或观测中所得结果,称为随机过程的一个实现。
若时间参变量T 是连续时刻的集合,则称这种随创机过程为连续参数随机过程,如水位过程、流量过程等。
若时间参变量T 是程为离散时刻的集合,则称这种随机过离散参数随机过程,也称为随机序列或时间序列。
如年、月径流程,年最大流量过程都是时间序列,也称水文时间序列。
(二)随机过程的数字特征随机过程)(t ξ在任一固定时刻的状态是随机变量,因此可按与前述随机变量同样的方法定义随机过程的数学期望和方差。
定义如下数学期望 )]([)(t E t ξμ= (8—11) 方差 })]()({[)(22t t E t μξσ-= (8—12)为了规划随机变量两个不同时刻状态间关系的密切程度,可定义随机变量的自相关函数为})()()]()()][()([{),(21221121t t t t t t E t t R σσμξμξ--= (8-13)(三)随权过程基本分类l 。
按统计性质的稳定性分类按随机过程的统计性质是否随时间而变化,可分成平稳和非平稳过程。
若随机过程统计数字特征不随时间的平移而变化,则称为平稳过程,否则为非平稳过程。
2.按不同时刻状态间的关系分类可分成独立过程和马尔柯夫过程。
若过程各状态相互独立,则称为独立随机过程。
在非独立随机过程中,最重要的一类是马尔柯夫过程,其特点是n t 时刻状态只与1-n t 时刻有关,而与1-n t 以前各时刻无关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
随机水文学 (交通大学 河海学院)
1. 研究背景
径流量
径流是指到达地面的 大气降水扣除蒸发、土壤 入渗、植物截留及洼地滞 蓄等水量后经地表、地下 汇入河流、湖泊或海洋的 水流总称。根据水源的特 性,可分为降雨径流、融 雪径流和冰川径流。根据
水流组成,可分为地表径
水文站原始年降水量数据
Hale Waihona Puke 1967-2009年4月份径流量
14000 12000 10000 8000 6000 4000 2000 0 1965 1970 1975 1980 1985 1990 系列1
1967-2009年5月份径流量
12000 10000 8000 6000 系列1 4000 2000 0 1965 1970 1975 1980 1985 1990
1
采用均值标准差法划分为五 个状态用1,2,3,4,5表示
表格链接
可以分别得到2010年4月和各 年4到5月的一步转移矩阵
2
总结
马尔可夫链是一种很重要的离散随机过程,简单说来就 是用来求出一个事件的后续发展可能,当已知“现在”时刻 过程的状态,那么过程“将来”的情况与“过去”的情况是 无关的。或者说,这种随机过程的将来只通过“现在”与 “过去”发生联系,如果一旦知道“现在”,那么“将来” 就和“过去”无关了。通过研究马尔可夫链,可观察后面的 发展状况,利用初始分布和一步转移概率就可以完全确定马 尔可夫链的统计规律。
流(表面径流)、壤中径 流和地下径流。
就 某 一 地 区 讲, 降 水 量 大, 径 流 量 就 大, 水 资 料 量 也 大。
2.马尔柯夫链对径流量的预测
一、马尔柯夫
马尔柯夫过程因其无后效性、遍历性和时齐性,在 科学研究、天气预测、农业预测、市场预测等方面 应用非常广泛。
二、马尔柯夫过程
马尔可夫过程是指具有以下特性的过程:过程X(t)(或系统) 在时刻t0所处的状态为已知的条件下,过程在时刻t>t0所处状 态的条件分布与过程在时刻t0之前所处的状态无关,只与时 刻t0所处的状态有关,这种特性称为马尔可夫性或无后效性。 则称X(t)为马尔可夫过程。
马尔柯夫链使用要求
马尔可夫链是满足下面两个假设的一种随机过程:
1、t+l时刻系统状态的概率分布只与t时刻的状态 有关,与t时刻以前的状态无关;
2、从t时刻到t+l时刻的状态转移与t的值无关。
2.1
以马尔柯夫链计算过程分析
思路
每年四、五月总径流量 计算2010年4月径流的概率分布(式1) 计算4月到5月的转移概率矩阵(式2) 两式相乘,得2010年5月径流量概率分布情况
