线性代数第2版课件-标准正交基和正交矩阵
合集下载
线性代数正交规范化ppt课件

x1x2x30. 它的基础解系为
1 0
1 0 ,2 1 .
1 1
把基础解系正交化,即合所求.亦即取
a21, a32[[11,,12]]1.
其 [1 ,中 2 ] 1 ,[1 ,1 ]2 ,于是得
1 a2 0 , 1
0 1 1 1 1 a311201221.
四、正交矩阵与正交变换
rr
其中
e ieiT[, i]
6 求规范正交基的方法
设1,2,,r是向量空V的 间一个,要 基求V
的一个规范正,就交是基要找一组两的 两单 正交
位 向 量 e1,e2,,er ,使e1,e2,,er与1,2,,r等
价,这样一个问 ,称题 为把 1,2,,r这个基
范正 . 交化 若 a 1,a2, ,ar为向 V 的 量一 空 , 个 间基
则有 [1 ,3 ] [2 ,3 ] 0
即
[[ 2 1,, 3 3]] x x1 1 2 xx 22xx 3300
解之得 x 1 x 3,x 2 0 .
若令 x31,则有 3
x1 x2
1 0
x3 1
由上可知1,2,3构成三维空间的一设n维向量 e1,e2,,er是向量空 V(V间
1 1 4
例3
设a1
2,a2
3,a31,试
用
施密
1
1
0
特正交化过程量 把规 这范 组正 .向交化
解
取 b1a1;
1 1
b2
a2 [a2,b21]b1
b1
3 1
4 6
2 1
5 3
1 1 1
;
b3a3[a3,b21]b1[a3,b22]b2
b1
1 0
1 0 ,2 1 .
1 1
把基础解系正交化,即合所求.亦即取
a21, a32[[11,,12]]1.
其 [1 ,中 2 ] 1 ,[1 ,1 ]2 ,于是得
1 a2 0 , 1
0 1 1 1 1 a311201221.
四、正交矩阵与正交变换
rr
其中
e ieiT[, i]
6 求规范正交基的方法
设1,2,,r是向量空V的 间一个,要 基求V
的一个规范正,就交是基要找一组两的 两单 正交
位 向 量 e1,e2,,er ,使e1,e2,,er与1,2,,r等
价,这样一个问 ,称题 为把 1,2,,r这个基
范正 . 交化 若 a 1,a2, ,ar为向 V 的 量一 空 , 个 间基
则有 [1 ,3 ] [2 ,3 ] 0
即
[[ 2 1,, 3 3]] x x1 1 2 xx 22xx 3300
解之得 x 1 x 3,x 2 0 .
若令 x31,则有 3
x1 x2
1 0
x3 1
由上可知1,2,3构成三维空间的一设n维向量 e1,e2,,er是向量空 V(V间
1 1 4
例3
设a1
2,a2
3,a31,试
用
施密
1
1
0
特正交化过程量 把规 这范 组正 .向交化
解
取 b1a1;
1 1
b2
a2 [a2,b21]b1
b1
3 1
4 6
2 1
5 3
1 1 1
;
b3a3[a3,b21]b1[a3,b22]b2
b1
线性代数(第二版)第六节Rn 的标准正交基

… , bn)T 为 Rn 中的两个向量,则 b1
T(a1,a2, ,an)b bn 2a1b1a2b2anbni n1aibi
称为向量 与 的内积. 显然, T R .
例如,设 = (1, 1, 1, 1)T , = (1, -2, 0, -1)T , = (3, 0, -1, -2)T , 则
如果一个正交向量组中的每一个向量都是单位
向量,则称该向量组为正交单位向量组.
由正交的定义可知,Rn 中的零向量与任意向量
都正交; 又由内积的性质
内积的性质
(1) T = T ; (2) (k )T = kT ; (3) ( + )T = T + T ; (4) T 0 , 且 T = 0 = 0 .
即 在 标 准 基 下 的 坐 标 为 (d1 , d2 , … , dn) , 恰 为 的各个分量.
设 在基 1 , 2 , … , n 下 的坐标 为 (x1 , x2 , … , xn)
则有 x11 + x22 + … + xnn =
二、向量的内积
1. 内积的定义 定义 2.18 设 = (a1 , a2 , … , an)T , = (b1 , b2
则对于任意 Rn, 可以表为 1 , 2 , … , n 的线
性组合,且表示法唯一, 即存在 a1 , a2 , … , an R , 使
= a11 + a22 + … + ann
则称组合系数 a1 , a2 , … , an 为 在基1 , 2 , … , n
下的坐标,记作 ( a1 , a2 , … , an ) .
第六节 Rn 的标准正交基
向量空间的基 向量的内积 向量的长度 标准正交基 正交矩阵
T(a1,a2, ,an)b bn 2a1b1a2b2anbni n1aibi
称为向量 与 的内积. 显然, T R .
例如,设 = (1, 1, 1, 1)T , = (1, -2, 0, -1)T , = (3, 0, -1, -2)T , 则
如果一个正交向量组中的每一个向量都是单位
向量,则称该向量组为正交单位向量组.
由正交的定义可知,Rn 中的零向量与任意向量
都正交; 又由内积的性质
内积的性质
(1) T = T ; (2) (k )T = kT ; (3) ( + )T = T + T ; (4) T 0 , 且 T = 0 = 0 .
即 在 标 准 基 下 的 坐 标 为 (d1 , d2 , … , dn) , 恰 为 的各个分量.
设 在基 1 , 2 , … , n 下 的坐标 为 (x1 , x2 , … , xn)
则有 x11 + x22 + … + xnn =
二、向量的内积
1. 内积的定义 定义 2.18 设 = (a1 , a2 , … , an)T , = (b1 , b2
则对于任意 Rn, 可以表为 1 , 2 , … , n 的线
性组合,且表示法唯一, 即存在 a1 , a2 , … , an R , 使
= a11 + a22 + … + ann
则称组合系数 a1 , a2 , … , an 为 在基1 , 2 , … , n
下的坐标,记作 ( a1 , a2 , … , an ) .
第六节 Rn 的标准正交基
向量空间的基 向量的内积 向量的长度 标准正交基 正交矩阵
第四章2正交矩阵

1 1 n n
设 1 (a11 ,, a1n ),,n (an1 ,, ann ) 是一个标准正交基,组成行列式 a11 a12 a1n a21 a22 a2 n Q . an1 an 2 ann
5
a11 a21 T QQ a n1
( 2 , 1 ) 1 1 , 2 2 1 . 1 , 2 ( 1 , 1 )
1 1 , 1 , 2
可用 1 , 2线性表示.而 可用 1 , 2 线性表示. 2 o. 否则, 2
16
可用 1 1 , 线性表示,此与 1 , 2 线性无关矛盾.
§2 正交矩阵
R n 的标准正交基和正交矩阵 一、
二、两组标准正交基之间的过渡矩阵 三、正交矩阵及其性质 四、施密特标准正交基的求法
1
R n 的标准正交基和正交矩阵 一、
平面上通常选择坐标轴上的单位向量(1,0)和 (0,1)组成的所谓标架对于平面上的所有向量 进行分解.为了研究几何问题有时需要旋转这 个标架得到新的标架 1 ,2 ,这两个向量仍然正 交,并且长度为1.这样的向量组称为标准正交 基. 定义 R n 中的n个向量 1 ,, n 的向量组, 如果两两正交,并且每个向量的长度为1,则称 为一个标准正交基.
1 1/ 2 1 1 2 2 2 (0,1,1) (1,0,1) ( ,1, ) ( , , ). 2 3/2 2 2 3 3 3
再标准化,
19
6 1 1 2, 2 2 , 2 2 3 T 3 3 3 . 3 1 1 1 1 ( ,0, ), 1 2 2
a12 a1n a11 a21 an1 a22 a2 n a12 a22 an 2 an 2 ann a1n a2 n ann 1 0 0 0 1 0 1 T E .Q Q . 0 0 1
设 1 (a11 ,, a1n ),,n (an1 ,, ann ) 是一个标准正交基,组成行列式 a11 a12 a1n a21 a22 a2 n Q . an1 an 2 ann
5
a11 a21 T QQ a n1
( 2 , 1 ) 1 1 , 2 2 1 . 1 , 2 ( 1 , 1 )
1 1 , 1 , 2
可用 1 , 2线性表示.而 可用 1 , 2 线性表示. 2 o. 否则, 2
16
可用 1 1 , 线性表示,此与 1 , 2 线性无关矛盾.
§2 正交矩阵
R n 的标准正交基和正交矩阵 一、
二、两组标准正交基之间的过渡矩阵 三、正交矩阵及其性质 四、施密特标准正交基的求法
1
R n 的标准正交基和正交矩阵 一、
平面上通常选择坐标轴上的单位向量(1,0)和 (0,1)组成的所谓标架对于平面上的所有向量 进行分解.为了研究几何问题有时需要旋转这 个标架得到新的标架 1 ,2 ,这两个向量仍然正 交,并且长度为1.这样的向量组称为标准正交 基. 定义 R n 中的n个向量 1 ,, n 的向量组, 如果两两正交,并且每个向量的长度为1,则称 为一个标准正交基.
1 1/ 2 1 1 2 2 2 (0,1,1) (1,0,1) ( ,1, ) ( , , ). 2 3/2 2 2 3 3 3
再标准化,
19
6 1 1 2, 2 2 , 2 2 3 T 3 3 3 . 3 1 1 1 1 ( ,0, ), 1 2 2
a12 a1n a11 a21 an1 a22 a2 n a12 a22 an 2 an 2 ann a1n a2 n ann 1 0 0 0 1 0 1 T E .Q Q . 0 0 1
标准正交基.ppt

第一页,编辑于星期二:四点 十分。
第二页,编辑于星期二:四点 十分。
第三页,编辑于星期二:四点。
第五页,编辑于星期二:四点 十分。
第六页,编辑于星期二:四点 十分。
第七页,编辑于星期二:四点 十分。
第八页,编辑于星期二:四点 十分。
第九页,编辑于星期二:四点 十分。
第十页,编辑于星期二:四点 十分。
第十一页,编辑于星期二:四点 十分。
第十二页,编辑于星期二:四点 十分。
第十三页,编辑于星期二:四点 十分。
第十四页,编辑于星期二:四点 十分。
第十五页,编辑于星期二:四点 十分。
第十六页,编辑于星期二:四点 十分。
第二页,编辑于星期二:四点 十分。
第三页,编辑于星期二:四点。
第五页,编辑于星期二:四点 十分。
第六页,编辑于星期二:四点 十分。
第七页,编辑于星期二:四点 十分。
第八页,编辑于星期二:四点 十分。
第九页,编辑于星期二:四点 十分。
第十页,编辑于星期二:四点 十分。
第十一页,编辑于星期二:四点 十分。
第十二页,编辑于星期二:四点 十分。
第十三页,编辑于星期二:四点 十分。
第十四页,编辑于星期二:四点 十分。
第十五页,编辑于星期二:四点 十分。
第十六页,编辑于星期二:四点 十分。
线性代数课件-正交矩阵

,b2,b3
且b 1
,b2,b3与a1
,
a2,a3等价.
令 3 3 k11 k22 , 为使
1, 3 2, 3 0 , 则 可推出
k1
3 , 1,
1 1
,
k2
3 , 2 ,
2 2
,
于是
3
3
3 , 1,
1 1
1
3 , 2 ,
2 2
2
,
1, 2 , 3 是与1, 2 , 3 等价的正交向量组 .
1 正交的概念 当 ( x, y) 0 时 , 称向量 x 与 y 正交. (orthogonal)
由定义知,若 x ,则 x 与任何向量都正交.
2 正交向量组的概念 若一非零向量组中的向量两两正交,则称该向
量组为正交向量组.
3 正交向量组的性质
定理1 若 n 维向量 α1,α2 , ,αr 是一组两两正交的 非零向量 , 则 α1,α2 , ,αr 线性无关.
1 1
a2 0 , 1
a3
1 1
2
0 1
2
2 . 1
四、正交矩阵与正交变换
1. 定义 若实矩阵 A 满足 AAT=ATA=I ,则称 A 为正交矩阵 .
2. 性质 1 A1 AT,
2 A 1 ,
3 AT , A1, AB也是正交方阵
4 A 为正交矩阵 A的行列向量组
证明 设有 1,2 , ,r 使 11 22 r 0
以a1T 左乘上式两端,得 11T1 0 由 1 0 1T1 1 2 0,
同理可得2 r 0. 故1,2 , ,r线性无关.
如:a1 1,0,0,a2 0,1,0,a3 0,0,1
b1 1,0,0,b2 1,1,0,b3 1,1,1
线性代数——正交矩阵PPT课件

是 R3 的一组基,
1
0
1
将其化为标准正交基. 解答见书上187页例4。
第9页/共11页
例5 设 1 , 2 , 3 , 4 是 R4 的一组标准正交基, 1 1 2 , 2 2 1 3 2
求 L(1 ,2 ) 的一组标准正交基.
作业: P162 14, 16, 17, 18(2), 19~24, 25(1), 26, 27, 28
2°特点: 设 1 ,2 , ,n 是 Rn 的一组标准正交基,
设 (12 n ), 则
Байду номын сангаас
T
1T 2T
1 2
nT
n
1T1 2T1
1T2 2T2
第1页/n共T111页 nT2
1Tn 2Tn
E
nTn
二、两组标准正交基间的过渡矩阵
设 1 ,2 , ,n 与 1 ,2 , ,n 是 Rn 的两组标准
k
则 1, 2 , , s 是与1 ,2 ,
的向量组.
i 2, 3, , s
, s等价且两两正交
第8页/共11页
2.在一组基的基础上,求标准正交基的步骤: 1°用施密特正交化方法, 将其化为正交向量组; 2°将正交向量组中每个向量单位化(也称标准化).
1 1 0
例4
已知1
0
,
2
1
,
3
1
故
QTQ E.
第2页/共11页
三、正交矩阵及其性质 定义2 实数域 R 上的 n 阶矩阵 Q 满足 QTQ E, 则
称 Q 为正交矩阵. 性质 (1) n阶矩阵Q 为正交矩阵 Q1 QT ;
进而, 给出等价定义: 如果 QQT E, 则Q 为正交矩阵.
2.6 标准正交基
则称a1 , a2 , … , an 为 向量 在基 1 , 2 ,, n 下的坐标, 记作 ( a1 , a2 , … , an ) .
二、向量的内积
1.Def .
给定Rn中向量
a1 a2 an
n i1
b1 b2 , bn
i j 0
T
1 0 0 1 2 0 0
0 0 , n 1
是两两正交的.
( i j ; i , j 1, 2 , ..., s )
则称向量组1, 2,…,s 为正交向量组. 正交向量组1,2,…,s 中无零向量.
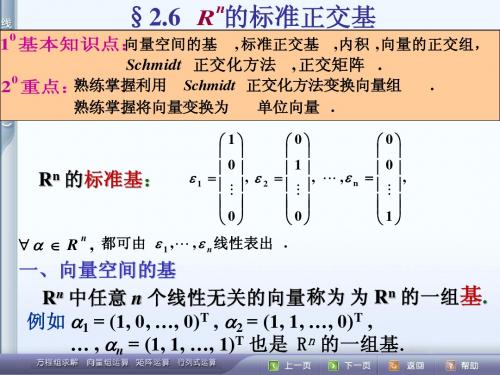
§2.6 R 的标准正交基
n
0
向量空间的基 , 标准正交基 , 内积 , 向量的正交组, 1 基本知识点: Schmidt 正交化方法 , 正交矩阵 . 0 熟练掌握利用 Schmidt 正交化方法变换向量组 . 2 重点:
熟练掌握将向量变换为 单位向量 .
1 0 0 0 1 0 , , , n , 1 2 0 0 1
a1 a2 an
n R ,
都可由 1 , , n 线性表出 .
a1 0 0
0 0 0 a2 a 1 1 a 2 2 a n n an 0
QTQ=
sin
co s sin
1 cos 0
0 1
线性代数2.6标准正交基

1
T
四、正交向量组 =0,则称 则称α α , β ∈ R n 如果 αTβ=0,则称α与β正交 定义2.20 定义2.20 设 α与β正交
αT β = 0
一般地, 一般地, 在 n 维空间Rn 中 ε 1 = ( 1 0 0 ... 0 )T 维空间R
ε 2 = ( 0 1 0 ... 0 )T
⋮
ε 3 = ( 0 0 1 ... 0)T
ε iT ε j= 0 ε i ε j i ≠ j 时, , 两两正交. 中的单位 单位向量组 Rn 中的单位向量组 ε1,ε2,…,εn 两两正交.
ε 1 , ε 2 ,..., ε n 称为Rn 中的 正交单位向量组. 称为R 正交单位向量组 单位向量组.
§2.6 Rn 的标准正交基 一、基,向量在基下的坐标 定义2.16 任意n 定义2.16 在Rn 中,任意n个线性无关的向量 α1 ,α 2 ,...,α n 称为Rn 的一组基. 称为R 的一组基 ε 1 = ( 1, 0, ..., 0 )T , ε 1 , ε 2 ,..., ε n 为Rn 的一组基. 如 的一组基. T ε 2 = ( 0, 1, ..., 0 ) , 称为Rn 的标准基, 自然基. 称为R 标准基, 自然基. 或
a1 a 2 ∈ Rn ∀α = ⋮ an
α和α的内积为 的内积为
α α = ( a1 a2
T
α Tα ≥ 0 α Tα = 0
a1 a n 2 2 2 ... an ) 2 = a1 + a2 +... + an = ∑ ai2 ⋮ i =1 ≥0 an
2 1 2 2 2 n
ka1 ka kα = 2 ⋮ kan
T
四、正交向量组 =0,则称 则称α α , β ∈ R n 如果 αTβ=0,则称α与β正交 定义2.20 定义2.20 设 α与β正交
αT β = 0
一般地, 一般地, 在 n 维空间Rn 中 ε 1 = ( 1 0 0 ... 0 )T 维空间R
ε 2 = ( 0 1 0 ... 0 )T
⋮
ε 3 = ( 0 0 1 ... 0)T
ε iT ε j= 0 ε i ε j i ≠ j 时, , 两两正交. 中的单位 单位向量组 Rn 中的单位向量组 ε1,ε2,…,εn 两两正交.
ε 1 , ε 2 ,..., ε n 称为Rn 中的 正交单位向量组. 称为R 正交单位向量组 单位向量组.
§2.6 Rn 的标准正交基 一、基,向量在基下的坐标 定义2.16 任意n 定义2.16 在Rn 中,任意n个线性无关的向量 α1 ,α 2 ,...,α n 称为Rn 的一组基. 称为R 的一组基 ε 1 = ( 1, 0, ..., 0 )T , ε 1 , ε 2 ,..., ε n 为Rn 的一组基. 如 的一组基. T ε 2 = ( 0, 1, ..., 0 ) , 称为Rn 的标准基, 自然基. 称为R 标准基, 自然基. 或
a1 a 2 ∈ Rn ∀α = ⋮ an
α和α的内积为 的内积为
α α = ( a1 a2
T
α Tα ≥ 0 α Tα = 0
a1 a n 2 2 2 ... an ) 2 = a1 + a2 +... + an = ∑ ai2 ⋮ i =1 ≥0 an
2 1 2 2 2 n
ka1 ka kα = 2 ⋮ kan
