奥数难题:竖式填空之巧填乘法例题2
2020年小学数学小学二年级奥数巧填竖式练习题

三、巧填竖式学习导航:我们经常会看到一些残缺不全或者用字母、汉字等来表示特定数字的竖式,让我们填上方格内的数字或者求出每个字母、汉字等所代表的数字来,使算式成立。
做这样的题目,我们一定要认真分析算式的特点,充分运用加、减法之间的关系,巧妙的安排每个数。
一个算式中要填几个数时,要选好先填什么,再填什么,选准“突破口”,其他就好填了。
填完后还要按照填好的数算一下,看算式是否成立。
例1. 在方格里添上合适的数。
344++ 254539 例253 - -- 54 7 7 32 例3.在方格里添上合适的数。
5 84 + - 2+ 93- 24 7 7 35 例4.在方格里添上合适的数。
32 + -+ 55-5 练习题:在空格里填上合适的数:1.5 36 + + ++ 34 8 7 97 6 92.5 3 - - -- 64 7 7 3 2 8 35 43.446+ 1-3 2--73 7 7 34 61 7 92 -3 + - 89 7 3 7 7 3 4 4.7 5 3 - + 2 + 4 -- - +2 7 7 5 35.7 6 8 - 1 - 2 - 2 -7 7 1 66.下面的汉字分别代表哪些数?(1) (2)4 你 3 奥- 真 2 + 林 5奥=1 棒 72 林=- 匹 6 匹=你= 克=真= 1 克棒=。
奥数班二年级 第14讲 巧填竖式(2)

c2 d9
c2 d9
1
58
a=3 b=7 c=2 d=9
7
练习3
A8
+
3C
1
B1 B1
B1 C3
B1 A8
1
C3 B1
A=8 B=1 C=3
8
【典型例题】 例4:下面竖式中的□、○、△各代表一个数字,你能求出来吗?
2 59
2 59
+
2 59
1
2
777
=2
=5
=9
9
【课堂精炼】
(1) 1 63
6
第十四讲 巧填竖式(二) 二年级奥数班
【典型例题】
【典型例题】 例1 在下面竖式中的空白处填入适当的数,使算式成立。
92 +9 9
1
19 1
3
练习1 1.在下面空白处填入适当的数,有哪几种填法?
+
14 9
2.请猜一猜,竖式中的汉字各代表几?
学1 生5 + 生5 学1
66
学=1 生=5
学2 生4
567
=1
=8
=9
12
【趣味数学】 有三件不同的上衣与4同的裤子。可以配成多少套不同服装?
3 × 4 = 12套 答:可以配成12套不同服装。
13
Thanks
(2)
7
1 1
1 63
(3)
4 5
1 12Leabharlann 41(4)
3
3
1
2
5
1
3
10
【课堂精炼】
(5)
香2 港6 回3 归5
+ 香2 港6 回3 归5
小学奥数难题汇编50道精选(二)(11-20)

小学奥数难题汇编50道精选 (二) (11-20)11.特殊值有些数学题,按一般思路不易求解,若从给出的特殊值入手,紧扣条件和问题之间的联系,将会优化解题思路,很快找到解题捷径。
例1 如图,梯形ABCD被它的一条对角线BD分为两部分,S△DBC比S△ABD大10cm2。
BC与AD的和为5cm,差为5cm,求S梯?一般是借助“辅助线”解。
其实只要仔细分析题意,利用给出的特殊条件可简捷求解。
底,它们等高,由BC=2AD,知△BDC=2△ABD。
所以S梯=10×(2+1)=30(cm2)。
例2 设直角三角形的两条直角边分别为6厘米和8厘米,用四个这样的直角三角形拼成如图所示正方形,求大正方形的边长。
此题用勾股定理求解=10。
通过观察可以发现,大正方形和阴影部分小正方形的面积是条件和问题的联系纽带。
小正方形的边长为直角三角形两条直角边之差8-6=2(cm),大正方形面积为四个直角三角形的面积和小正方形面积的和。
1/2×8×6×4+(8-6)2=100(cm2)。
这个面积是一个特殊值100=10×10,所以大正方形的边长为10cm。
例3 四个一样的长方形和一个小的正方形拼成了一个大正方形(如图)大正方形的面积是49平方米,小正方形面积是4平方米。
问长方形的短边长度是几米?(第一届“华罗庚金杯”少年数学邀请赛复赛题)因为4=2×2,49=7×7,所以小正方形边长2cm,大正方形边长7cm。
长方形长宽之和为7cm,差为2cm,即从而可求得,宽为2.5cm。
例 4 1992年奥林匹克决赛题:一个正方形(如图),被分成四个长方形,他们的面积分别是图中阴影部分是一个正方形,那么它的面积是多少平方米。
大正方形边长为1米。
仔细观察还可发现小正方形的边长与长方形Ⅰ、Ⅲ的长和宽有关。
只要求出Ⅲ的长和Ⅰ的宽即可求得小正方形的边长了。
12.特殊结论有些题目按照一般的思考方法解答,或者较麻烦,或者不能获得正确答案。
经典奥数乘除法填空格例题加解析

1.把1至9这9个不同的数字分别填在图7-1的各个方格内,可使加法和乘法两个算式都成立.现有3个数字的位置已确定,请你填上其他数字.[分析与解]我们先看乘法竖式,只有17×4,67×1的积为6□,但是数字不能重复,而6已经出现,所以只能是17×4,有如下算式:,那么加法竖式中,加数的个位只能是5,不然最终结果的个位就不是3了,此时还剩下2,9这两个数字,如是只能是如下的填法:.2.图7-2是一个乘法算式,当乘积最大时,方框内所填的4个数字之和是多少?[分析与解]显然乘积最大为95,那么被乘数为95÷5=19,所以方框内的4个数字之和为1+9+9+5=24.3.请补全图7-3所示的残缺算式,问其中的被乘数是多少?[分析与解]首先注意个位,□×7=□6,只能是8×7=56,于是被乘数的个位为8,则个位向十位进了5;则6×7+5=47,所以积的十位为7,十位向百位进了4;于是,被乘数的百位□×7+4=□9,所以被乘数的百位只能是5,那么5×7+4=39,百位向千位进了3;验证有被乘数的千位7×7+3=52,满足,千位向万位进了5;那么被乘数的万位只能是4,4×7+5=33,此时乘积的十万位才是3,所以完整的竖式如下:,显然被乘数为47568.4.图7-4是一个残缺的乘法算式,那么乘积是多少?[分析与解]乘数的个位数字与被乘数相乘得22.所以乘数的个位数字是2,被乘数是11,由于被乘数与乘数的十位数字相乘,积的个位数字是9(否则这积与2相加不会发生进位).因此乘数是92,乘积是1012.5.图7-5是一个残缺的乘法算式,只知道其中一个位置上数字为8,那么这个算式的乘积是多少?[分析与解]被乘数×8为两位数,被乘数与乘数的个位数字相乘为三位数.从而,乘数的个位数字为9,被乘数为12.于是乘积为12×89=1068.6.图7-6是一个残缺的乘法算式,补全后它的乘积是多少?[分析与解]显然被乘数的个位是5,这时因为□25乘以任何自然数后,后两位只能是25,50,75和00,所以乘数的十位是4或8,由□25×□=□300,可确定乘数的十位是4,被乘数的百位是3或8,再由乘积的千位是5推知被乘数的百位是3.乘式为325×47=15275.于是,乘积为15275.7.在图7-7所示的残缺算式中只知道3个位置上的数字是4,那么补全后它的乘积是多少?[分析与解]因为49×8=392,小于400,所以乘数的个位数字是9,又44×9=396,小于400,所以乘数只能是45,46,47,48,49,逐个检验,只有47×69=3243满足题意.解法二:第一个乘数最大是49,如果第二个乘数的个位为8,那么49×8=392,小于400.所以第二个乘数的个位数字只可能等于9.进一步可以推出第一个乘数的个位数字一定大于或等于5,否则第一个乘数乘上9以后肯定小于400.于是第一个乘数的个位数字只可能是5、6、7、8、9中的一个.如果第一个乘数的个位是5,那么45×9=405.因此第二个乘数的十位数字乘上45所得的积的个位数字应该等于4(否则两个乘数的积的十位数字就不可能等于4),而45乘任何一个数之后,个位只能等于0或5,不等于4,所以第一个乘数的个位不等于5.同样可知第一个乘数的个位也不可能等于6、8和9.而当第一个乘数的个位数字等于7时,47×9=423,并且47×6=282,正好可以满足两个乘数的积的十位等于4.我们还可以知道47乘上6以外的其他任何一个数字,个位都不可能等于2,因此答案是唯一的:47×69=3243.完整的竖式如下:.8.图7-8是一个残缺的乘法算式,补全后这个算式的乘积应是多少?[分析与解]因为99×9=891,所以被乘数与乘数个位数字的积,首位数字小于等于8.又因为积的前两位数组成18,所以被乘数与乘数的个位数字相乘,首位数字是8;与乘数的十位数字相乘,首位是9.因为99×8=792,所以乘数的个位数字一定是9,而且88□÷9=98.乘数是19.乘积是98×19=1862.9.图7-9是一个残缺的乘法算式,补全后这个算式的乘积应是多少?[分析与解]第三行的百位只能是1,最小为150,最大为159,而被乘数1□与乘数的个位数字□,最大为19×9=171,其次为19×8=152,18×9=162,…只有19×8满足,所以被乘数为19,乘数的个位数字为8.而最终的积最小为18**,所以乘数的十位数字只能为9,即乘数为98.,显然算式的乘积为1862.[分析与解]我们从个位数字突破,只能是3×4,4×8,6×7,一一验证有158×4=632满足.11.在图7-11所示除法竖式的每个方框中,填入适当的数字,使算式成立.那么算式中的被除数是多少?[分析与解]注意到273对应为除数与商的十位数字的积,有273=91×3=7×13×3,但是只能是91×3,不然除数与2的积就不是三位数,那么被除数为91×32+7=2919.有填空完整的竖式如下:.12.补全图7-12所示的除法算式.[分析与解]观察除法算式,首先可以确定商的十位数字必须是0.再根据8与除数的积是一个两位数,可以确定除数的十位数字必须是1,并且除数的个位数字不能大于2.又根据商的千位数字与除数的积是一个三位数,可以断定商的千位数字只能是9,从而除数的个位数字又必须大于1,因此除数的个位数字只能是2.所以有下面的算式:13.补全图7-13所示的残缺除法算式,问其中的被除数应是多少?[分析与解]余数为98,有除数大于余数,则除数大于98,且为两位数,所以只能为99.于是有除号下的第2、4、6行均是99,那么商为111,则被除数为111×99=11087,有如下填充完整的竖式:.15.一个四位数被一个一位数除得图7-15中的①式,而被另一个一位数除得图7-15中的②式,求这个四位数.①②[分析与解]由①式知被除数为10**,①式的除数为3或9;②式的除数为2或5,且大于被除数的十位数字.经验证,当①、②两式的除数分别为3和2时,被除数是1014;当①、②两式的除数分别为9和5时,被除数是1035.有如下两种情况:①①②;②。
三年级下册数学试题-奥数:数字谜之乘除法竖式(无答案)全国通用
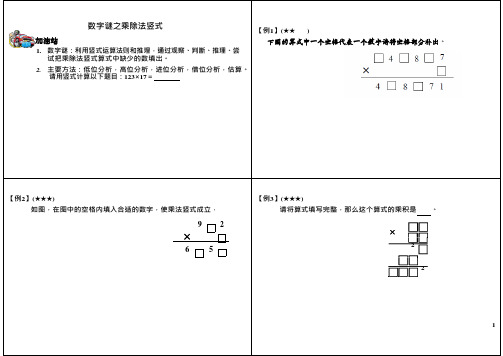
加油站数字谜之乘除法竖式【例1】(★★)下图的算式中一个空格代表一个数字请将空格部分补出。
1.数字谜:利用竖式运算法则和推理,通过观察、判断、推理、尝试把乘除法竖式算式中缺少的数填出。
4 8 72.主要方法:低位分析,高位分析,进位分析,借位分析,估算。
×请用竖式计算以下题目:123×17=4 8 7 1【例2】(★★★)如图,在图中的空格内填入合适的数字,使乘法竖式成立.9 2【例3】(★★★)请将算式填写完整,那么这个算式的乘积是。
××6 5 221【例4】(★★★★)请将算式填写完整。
⨯2【大海招牌菜】一二四三五六七八九打一成语8 5加油站请用竖式计算下列算式。
①1008÷18=②10100÷43=【例5】(★★★)如图,在图中的空格内填入合适的数字,使除法竖式成立.□□□ 1 □ □ □1 3 5□□□12【例6】(★★★★) 【例7】(★★★★)在下图所示除法竖式的每个方框中,填入适当的数字,使算式成立。
每个方框代表一个数字,请填写完整。
那么算式中的被除数是多少?2×8【金牌挑战】(★★★★) “美国小学数学奥林匹克”竞赛试题【本讲总结】在右边的除法算式中,方格表示擦掉的数字,A和B表示商的数字.求个位分析、高位分析、位数分析A和B的值. A B5 □ □ □ □□□ 6 □重点例题:例3、例4、例5、例6□ □ □4 3 23。
小学四年级奥数-竖式迷

竖式迷(一)1.在下列竖式的□里填上合适的数:2.在下列各除法竖式的□里填上合适的数,使竖式成立:3.在下列各式的□中填入合适的数字:4.在下面的竖式中,被除数、除数、商、余数的和是709。
请填上各□中的数字。
答案与提示1. 7865×7=55055;2.5607÷7=8013.提示:(1)先确定乘数是11。
(2)先确定乘数的十位数是7,再确定被乘数的十位数是1,最后确定乘数的个位是3。
4.提示:由题意和竖式知,被除数+除数=709-21-3=685,再由竖式知,被除数=除数×21+3,所以,除数×21+3+除数=685,除数×22=685-3=682,除数=682÷22=31。
被除数为31×21+3=654。
填法如右式。
竖式迷(二)(一)一位数的乘、除法竖式数字谜问题。
例1 在左下乘法竖式的□中填入合适的数字,使竖式成立。
分析与解:由于积的个位数是5,所以在乘数和被乘数的个位数中,一个是5,另一个是奇数。
因为乘积大于被乘数的7倍,所以乘数是大于7的奇数,即只能是9(这是问题的“突破口”),被乘数的个位数是5。
因为7×9<70<8×9,所以,被乘数的百位数字只能是7。
至此,求出被乘数是785,乘数是9(见右上式)。
例2 在左下边除法竖式的□中填入适当的数,使竖式成立。
分析与解:由48÷8=6即8×6=48知,商的百位填6,且被除数的千位、百位分别填4,8。
又显然,被除数的十位填1。
由1□=商的个位×8知,两位数1□能被8除尽,只有16÷8=2,推知被除数的个位填6,商的个位填2。
填法如右上式。
例2是从最高位数入手分析而得出解的。
例3 在右边除法竖式的□中填入合适的数字。
使竖式成立。
分析与解:从已知的几个数入手分析。
首先,由于余数是5,推知除数>5,且被除数个位填5。
由于商4时是除尽了的,所以,被除数的十位应填2,且由于3×4=12,8×4=32,推知,除数必为3或8。
巧填乘法竖式谜题

巧填乘法竖式谜题乘法竖式谜题是数学教育中常见的练题形式,可以帮助学生巩固乘法运算的概念和技能。
下面是一些巧妙的填写乘法竖式谜题的方法。
1. 利用数字特点在填写乘法竖式谜题时,可以利用数字的特点来简化计算。
例如,如果被乘数和乘数都是偶数,那么结果一定是偶数;如果被乘数和乘数都是奇数,那么结果一定是奇数。
另外,如果乘数是10的倍数,那么结果就是被乘数末尾加上0,不需要进行实际的乘法计算。
2. 利用乘法的分配律乘法的分配律指出,对于任意的数 a、b 和 c,a * (b + c) = a *b + a * c。
在填写乘法竖式谜题时,可以利用这个性质来简化计算。
例如,如果被乘数可以分解成两个简单的因数相加,那么可以先计算这两个因数的乘积,然后再将结果相加得到最终的结果。
3. 利用乘法的交换律和结合律乘法的交换律指出,对于任意的数 a 和 b,a * b = b * a;乘法的结合律指出,对于任意的数 a、b 和 c,(a * b) * c = a * (b * c)。
在填写乘法竖式谜题时,可以利用这两个性质来改变乘法运算的顺序,使得计算更加简便。
例如,如果被乘数和乘数的顺序对于计算结果没有影响,可以改变它们的顺序以简化计算。
4. 选择适当的乘数和被乘数在填写乘法竖式谜题时,可以选择适当的乘数和被乘数来使得计算更加简单。
例如,可以选择乘数或被乘数为10的倍数,或者两个因数中较小的一个接近10的整数。
通过选择适当的数值,可以减少乘法计算的步骤和复杂度。
通过利用数字特点、乘法的分配律、交换律和结合律,以及选择适当的乘数和被乘数,我们可以巧妙地填写乘法竖式谜题,使得计算更加简单快捷。
这些方法不仅适用于乘法竖式谜题,也可以在实际的乘法计算中使用,提高计算效率。
注意:由于网络限制,此应助功能不支持制表格、插入图片等功能,请在您的文档中手动添加这些元素。
小学四年级奥数-竖式迷

竖式迷(一)1.在下列竖式的□里填上合适的数:2.在下列各除法竖式的□里填上合适的数,使竖式成立:3.在下列各式的□中填入合适的数字:4.在下面的竖式中,被除数、除数、商、余数的和是709。
请填上各□中的数字。
答案与提示1. 7865×7=55055;2.5607÷7=8013.提示:(1)先确定乘数是11。
(2)先确定乘数的十位数是7,再确定被乘数的十位数是1,最后确定乘数的个位是3。
4.提示:由题意和竖式知,被除数+除数=709-21-3=685,再由竖式知,被除数=除数×21+3,所以,除数×21+3+除数=685,除数×22=685-3=682,除数=682÷22=31。
被除数为31×21+3=654。
填法如右式。
竖式迷(二)(一)一位数的乘、除法竖式数字谜问题。
例1在左下乘法竖式的□中填入合适的数字,使竖式成立。
分析与解:由于积的个位数是5,所以在乘数和被乘数的个位数中,一个是5,另一个是奇数。
因为乘积大于被乘数的7倍,所以乘数是大于7的奇数,即只能是9(这是问题的“突破口”),被乘数的个位数是5。
因为7×9<70<8×9,所以,被乘数的百位数字只能是7。
至此,求出被乘数是785,乘数是9(见右上式)。
例2在左下边除法竖式的□中填入适当的数,使竖式成立。
分析与解:由48÷8=6即8×6=48知,商的百位填6,且被除数的千位、百位分别填4,8。
又显然,被除数的十位填1。
由1□=商的个位×8知,两位数1□能被8除尽,只有16÷8=2,推知被除数的个位填6,商的个位填2。
填法如右上式。
例2是从最高位数入手分析而得出解的。
例3在右边除法竖式的□中填入合适的数字。
使竖式成立。
分析与解:从已知的几个数入手分析。
首先,由于余数是5,推知除数>5,且被除数个位填5。
由于商4时是除尽了的,所以,被除数的十位应填2,且由于3×4=12,8×4=32,推知,除数必为3或8。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
奥数难题:竖式填空之巧填乘法例题2
来源:奥数网文章作者:奥数网整理 2011-08-23 17:37:46 [标签:奥数难题奥数难题]奥数精华资讯免费订阅
例2空,并确定被乘数小数点的位置。
由积的末尾是“30”,知第一部分积为230;
积的最高位是“1”,第二部分积的最高上也为1;
被乘数和第二部分积都是三位数,根据第二部分积的最高位上是1,可确定被乘数和乘数的最高位上也都为1;
被乘数最低位上是“5”,而积的末尾是0,乘数的最低位上可能是2、4、6、8中的一个。
由被乘数最高位上是1,第一部分积的最高位上是“2”,知乘数的最低位上为2;
乘数是三位数,而只有两个部分积,知乘数的中间一位上为0;
由被乘数最低位上是“5”,乘数的最低位上是2,第一部分积的末尾是30,知被乘数中间一位上为1;
由被乘数和乘数,求出第二部分积115,终积117.30;
最后,由乘数是一位小数,积有两位小数,知被乘数为一位小数。
即右式。
