捷联惯导误差方程_ENU_完整版
激光陀螺捷联惯性导航系统的误差参数标定

Abstract:In the inertial devices calibration,in general the test equipment must perform north—seeking and
level-adjusting to eliminate the influence of the ground velocity and the acceleration of gravity,but this is not suitable for the environment of shooting range and other fields.According to the error equation of laser gyro strapdown inertial navigation system,using 12-position calibration method to counteract the influence of the ground velocity and the
文章编号:1005-6734(2008)03-0306-04
中国惯性技术学报
Journal of Chinese Inertial Technology
v01.16 No.3 Jun.2008
激光陀螺捷联惯性导航系统的误差参数标定
杨孟兴,徐兵华
(中国航天时代电子公司第十六研究所,西安710100)
摘要:惯性器件标定一般都必须对北和调平,以消除地速及重力加速度的影响,但是不适合在靶场及其它野战
中国惯性技术学报 表1组件误差参数标定位置顺序
Tab.1 Calibration order of error parameter of component,
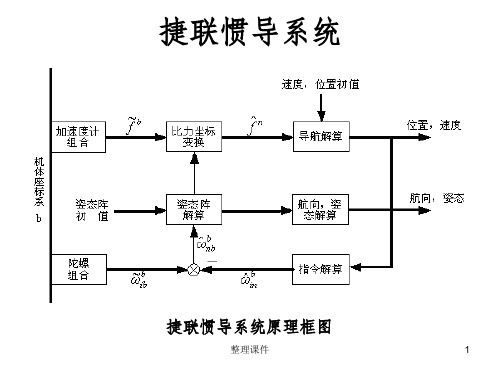
捷联惯导

%捷联惯导系统
%姿态矩阵初值
T(:,:,1)=ctn(:,:,1);
%T(:,:,1)=inv([0,0,-g(1);0,w*cos(pi/4),w*sin(pi/4);g(1)*w*cos(pi/4),0,0])*[fb(1,1),fb(2,1),fb(3,1);wib(1,1),wib(2,1),wib(3,1);
at(:,t)=[0;0;y0(t)*v(2,t)];
a(:,t)=[1,0,0;0,cos(y(t)),-sin(y(t));0,sin(y(t)),cos(y(t))]*at(:,t);
v(1,t+1)=v(1,t)+a(1,t)*delt;
v(2,t+1)=v(2,t)+a(2,t)*delt;
l(t+1)= l(t)+v(1,t+1)./(rm(t+1)+h(t))./cos(al(t))*delt;
h(t+1)=h(t)+v(3,t+1)*delt;
end
for t=tf+1:tf*2
y0(t)=0;
y(t)=y(tf);
at(:,t)=[0;0;0];
% wib(3,1)*fb(2,1)-wib(2,1)*fb(3,1),wib(1,1)*fb(3,1)-wib(3,1)*fb(1,1),wib(2,1)*fb(1,1)-wib(1,1)*fb(2,1)];
%T(:,:,1)=[0,0,sec(a0(1))/g(1)/w;tan(a0(1))/g(1),sec(a0(1))/w,0;-1/g(1),0,0]*[fb(1,1),fb(2,1),fb(3,1);wib(1,1),wib(2,1),wib(3,1);
P18捷联惯导系统误差传播特性

考虑到
b b b δω ib = ω ib − ω ibm
b E δω ib = q −1δω ib q
b E ω iE = q −1ω IE q
—— 速度误差方程的分量展开形式
位置误差、 位置误差、系统误差
根据经度、 根据经度、纬度的定义
取小偏差, 取小偏差,得
VN ɺ ϕ =− R ɺ = VE sec ϕ λ R δV N ɺ δϕ = − R ɺ = δVE sec ϕ + VE sec ϕ ⋅ tgϕ ⋅ δϕ δλ
R R
4、系统误差方程 、 由数学平台误差角方程、速度误差方程、 由数学平台误差角方程、速度误差方程、位置误差方程组成 经度误差方程仍可单独考虑 静基座条件下, 静基座条件下,捷联惯导系统误差传播特性与平台式一致
b −1 Im C E I E I E iE E E r
第一项: 第一项:δAIE = ∆AE 第二项: 第二项: AIE = AE 第三项: 第三项:
[
[
——速度误差方程的矢量表达式 速度误差方程的矢量表达式
∆AN
AN
Aζ
]
∆Aζ
T
]
T
Φ = [α
β γ]
T
E ω iE
VN − R V = E + ω e cos ϕ R V E tgϕ + ω e sin ϕ R
b − E ω IEC = q C1ω iEC q C
1 1 −1 E −1 1 −1 E b −1 − qδω ib qC − qq ω iE qqC + qq C ω iEC qC qC1 可得 2 2 2 1 1 E 1 E E = δω ib δq − ω iE δq + δqω iEC 2 2 2 ɺ Φ Φ δq = 1 + 另有 ɺ 代入上式, 代入上式,并忽略二阶小量 δq = 2 2 ɺ = δω E (1 + Φ ) − ω E (1 + Φ ) + (1 + Φ ) ω E Φ ib iE iEC 2 2 2 ɺ δq =
《捷联惯导系统》
q1
q 2
q
3
1
2 1
2 1
2
1 T 11 T 22 T 33 1 T 11 T 22 T 33 1 T 11 T 22 T 33
4 4
q1 q 0 q2q0
T32 T13
T23 T31
4q3q0 T21 T12
sig(qn1)sig(qn0)[sig(Tn32T23)] sig(qn2)sig(qn0)[sig(Tn13T31)] sig(qn3)sig(qn0)[sig(Tn21T12)]
t t
t t
θ d t Φ ()d t
t
t
表征旋转的另一种形式: Φu
qcos Φ Φsin Φ 2Φ 2
Φ n b b (t) 1 2 Φ ω b n b (t) 1 1 2 Φ (Φ ω b n b (t))
整理课件
10
捷联惯导系统
泰勒级数展开、曲线拟合的方法(几个采样角就为几子样算法)
qˆi qˆ02 qˆ12 qˆ22 qˆ32
整理课件
8
捷联惯导系统
2.3.4 从姿态矩阵中提取姿态角 θ∈﹙-90,90﹚度 γ∈﹙-180,180﹚度 Ψ∈﹙-180,180﹚度 或 Ψ∈﹙0,360﹚度
c o sc o s s in s in s in s in c o s s in c o s c o ss in s in C b n c o ss in s in s ic n o s c o s s in c o s s in c o s s in s in c o s c c o o s s c o s s in
个不同的轴的三个角度来确定。把载坐标系作动坐标系,导航系为参 考系则 、 和 即为一组欧拉角。
第讲:捷联惯导系统温度误差特性建模

第2讲:捷联惯导系统温度误差特性建模惯性器件温度误差特性的测试与建模1 光学陀螺的温度误差对于工程化要求的光学陀螺,为适应各个领域的应用,一般要求其具有较宽的工作温度范围(一般为-40~60℃),可以在不同温度环境下正常工作。
零偏与标度因数是衡量激光陀螺性能的两个重要指标,这两项指标受温度的影响很大。
1.1 激光陀螺的温度特性有源谐振腔激光陀螺原理图激光陀螺外界温度变化时,使激光陀螺本体产生热膨胀,导致激光环路的程长增长,零偏和标度因数都会发生变化。
而且,外界温度变化会影响到信息处理电路元器件的工作状态,产生数据读出误差。
即使温度不发生变化,不同温度点的零偏和标度因数也不相同,因为温度不同陀螺本体内部物理结构会产生一些常值的变化。
总之,温度变化和绝对温度值能够影响到谐振腔激活介质增益、顺时针、逆时针光波的自作用和互作用、反射镜特性参数、闭锁锁区、工作气体流动速度、谐振腔长度变化、谐振腔工作模式、压电陶瓷歪扭等,导致零偏和标度因数的变化。
(1) 室温(2) 变温室温和变温条件下的某型激光陀螺捷联系统三轴测试数据1.2 光纤陀螺的温度特性干涉型光纤陀螺结构图构成光纤陀螺的主要器件如光纤线圈、集成光学器件、光源、耦合器等对温度较为敏感,所以当工作环境温度发生变化时,在陀螺的输出信号中将产生非互易相位误差。
由温度变化造成的非互异性误差,是导致光纤陀螺零位漂移和标度因数不稳定的主要原因,严重影响着光纤陀螺仪全温度下的精度。
此外,从工程应用考虑,有的应用场合要求尽可能缩短陀螺启动后达到热平衡的过程,使其迅速进入预定的工作状态,光纤陀螺启动后需要较长的热稳定过程,不能满足使用要求。
2 温度误差与补偿方法目前为了降低和补偿温度对惯性器件(陀螺与加速度计)精度的影响,常采用四种方法:1、研制对温度不敏感的惯性器件。
从惯性器件的设计出发,使惯性器件的布局、零件的材料和结构形状满足对温度不敏感的要求。
2、在结构中增加负温度系数的材料、元件,以抵消温度变化引起的另外有关材料的物理参数的变化,补偿温度对惯性器件精度的影响。
捷联惯导

由于在L的定义域内cosL永远为正,所以 cos 与C31同号
利用 C31,主 的正负值可确定真值 :
主
C31 0
= 主 180 C31 0, 主 0 主 180 C31 0, 主 0
飞行器运动引起地理坐标系相对于地球坐标系的三个角速度分量为:
t etN
VEt Rn h VEt tan L Rn h
t etU
接上文
将前两式求和得:
t itE t VN Rm h
t itN
VEt ie cos L Rn h VEt ie sin L tan L Rn h
t VEt、VN 地理坐标系下的东向和北向速度
方向余弦矩阵(位置矩阵)Ce
平台坐标系与地球坐标系转动关系为:
p
Xp Xe p Y C Y p e e Z Z e p
其中
C11 C12 C13 sin sin L cos cos sin sin sin L sin cos cos sin cos L Cep C21 C22 C23 cos sin L cos sin sin cos sin L sin sin cos cos cos L C C C33 cos L cos cos L sin sin L 32 31
1
主
主 , T33 0时 主 180 , T33 0且 主 0 180 , T33 0且 主 0 主 再根据定义域与T中元素的符号得到各角真值: G主 , T22 0, G主 0 G G主 360 , T22 0, G主 0 G主 180 , T22 0
惯导原理捷联惯导基本算法与误差课件

目录
惯导系统概述捷联惯导系统惯导系统的误差补偿技术惯导系统在各领域的应用未来惯导技术的发展趋势总结与展望
01
CHAPTER
惯导系统概述
惯性导航系统(INS)是一种自主式导航系统,通过测量载体在三个轴上的加速度和角速度,结合初始位置、速度和姿态信息,计算出载体当前的位置、速度和姿态。
总结与展望
随着科技的进步,提高惯导系统的精度是未来的重要发展方向。
更高精度
多模融合
微型化与集成化
人工智能优化
将惯导与其他导航手段(如GPS、北斗等)进行融合,以提高导航定位的可靠性和精度。
随着微电子和集成电路技术的发展,实现小型化、低功耗的惯导系统是未来的趋势。
利用人工智能技术对惯导系统进行优化,提高其性能和适应性。
THANKS
感谢您的观看。
定义
不依赖外部信息,隐蔽性好;可在各种复杂环境中工作;导航信息连续性好;但误差随时间积累,长时间工作导航精度较低。
特点
02
CHAPTER
捷联惯导系统
捷联惯导系统是一种基于陀螺仪和加速度计的导航系统,通过测量载体相对惯性空间的角速度和加速度,计算出载体相对于地球的位置、速度和姿态信息。
陀螺仪能够测量载体相对惯性空间的角速度,加速度计能够测量载体相对于地球的加速度,通过积分运算,可以得到载体的位置、速度和姿态信息。
地球模型误差主要包括地球赤道隆起、地球重力场模型误差等,可以采用高精度地球模型进行减小或消除。
加速度计误差主要包括零点误差、刻度因数误差和非线性误差等,可以采用数字补偿或离线校准等方法进行减小或消除。
捷联惯导系统的误差主要包括陀螺仪误差、加速度计误差、地球模型误差和信号处理误差等。
捷联式惯导安装误差测量、补偿方法

link appraisement 中国直升机设计研究所中国科技信息2021年第8期·CHINA SCIENCE AND TECHNOLOGY INFORMATION Apr.2021◎航空航天画线法航向误差测量的操作流程如下:将直升机顶水平,保证直升机的水平基准与地理系水平面重合;在前后机身中轴线定位孔分别吊铅垂线;在地理系水平面上分别作出两条铅垂线在水平面上的投影;将两个铅垂线在水平面上的投影点连成直线;用角度测量工具测量投影点连线与正北的夹角α;启动捷联式惯导,记录捷联式惯导输出的真航向角β;计算航向误差θ,θ=α-β。
激光跟踪仪测量法激光跟踪仪是可跟踪测量空间中点的坐标的高精度测量设备。
激光跟踪仪测量法是通过测量捷联式惯导安装支架上的航向基准工艺孔的坐标,通过计算得到航向误差的测量方法。
图2为捷联式惯导安装支架,捷联式惯导安装时航向基准与安装支架的航向基准贴靠,测量安装支架的航向基准面与直升机纵轴面的夹角即可代表捷联惯导与直升机的航向误差。
为测量方便,在安装支架上加工两个工艺孔,工艺孔圆心的连线与安装支架的航向基准面平行。
激光跟踪仪测量法的操作流程如下:将直升机顶水平,保证直升机的水平基准与地理系水平面重合;以直升机上预制的工艺基准孔为基准建立激光跟踪仪测量坐标系;将反射器分别放置在捷联式惯导安装支架上的工艺孔1和工艺孔2的位置,分别测量捷联式惯导安装支架上的工艺孔1、工艺孔2的坐标,记为(X 1、Y 1)、(X 2、Y 2);计算航向误差角θ,θ=arctan[(X 2-X 1)/(Y 2-Y 1)]。
该误差测量方法借助高精度的激光跟踪仪进行测量,与画线法相比,减少了误差测量过程中人的参与,因此具有操作简单的优点,同时也具有更高的测量精度,推荐使用该误差测量方法。
高精度捷联式惯导测量法高精度捷联式惯导测量法是在捷联式惯导安装位置处安装比直升机上的捷联式惯导更高精度等级的捷联式惯导,利用该高精度捷联式惯导测量处于水平状态、机身中轴线与真北重合直升机的俯仰角、横滚角和真航向角,该俯仰角、横滚角和真航向角即为捷联式惯导的安装误差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
固定指北式捷联惯导误差传播方程(东北天坐标系):
()()()()()I I I I I
X t F t X t G t W t =+ 式中, T
181
I E
N U E N U b x b y b z r x r y
r z x y z
X L h ϕϕϕδυδυδυδ
δλδ
εεεεεε⨯⎡⎤=∇∇∇⎣⎦
0sin tan cos E
E
ie ie N N L L
L R h R h E N U E N U bx by bz rx ry rz x y z L h υυωωϕϕϕδυδυδυδδλδεεεεεε+
-+
++=⎛⎫
⎪⎝
⎭
⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣
⎦∇∇∇
1112131112132
2122232122232
2
3132333132
10000
000
()1sin tan 0
00sin 0
000()
1cos 0
tan 0
cos sec 0
tan ()
N
M M N
E
E
ie ie N M N N N
E
E
E
ie ie N M N N N C C C C C C R h R h L L L
C C C C C C R h R h R h R h L L
L L
L
C C C C C R h R h R h
R h
R h υυυυωωυυυυωω-
++-+
-
--++++++
-
+++++⎛⎫ ⎪⎝
⎭2332
1112132
tan 0tan 2sin tan 2cos 2cos sec 2sin 0
()0
2sin tan 2cos N
U
E N
E U E N E
E
ie ie ie ie U N N U
M M N N
N N U
N
E
E ie ie U E N M M C L
f f L L L
L L L L C C C R h
R h
R h
R h R h
R h f f L L L R h R h R h υυυυυυυυυυωωωυωυυυυυωω---
+
-+
+
+++++++--+-
-
-++++⎛⎫ ⎪⎝⎭
⎛⎫ ⎪
⎝⎭
22
2122232
22
3132332
2
2
tan sec 0000000
()202cos 02sin 0000000()
1000000
0000000000()
sec 00000sec tan 0se ()
E U N
E
N N N
E N
E
ie ie N E E
N M N N
M M E
E
N N N L L C C C R h R h f f L L C C C R h R h
R h R h
R h L L L R h R h
R h υυυυυυυυωωυυυυ-+++-+
--+++-++-
+++⎛⎫ ⎪⎝⎭
⎛⎫
⎪⎝
⎭
c 00000000000000100000000000000000000000000000000000000000000000000000000000000000010000000000000000010000000000000000010000000000000000010000000000000000010000000000000000000
x y z ax ay L
T T T T T -
-
-
--10
az
T E N U E N U bx by bz rx ry rz x y z
L h ϕϕϕδυδυδυδδλδεεεεεε-⎡
⎤⎢
⎥⎢
⎥⎡⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢
⎥⎢⎢
⎥⎢⎢⎥⎢⎢⎥⎢⎢
⎥⎢⎢⎥⎢⎢
⎥⎢⎢
⎥⎢⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢
⎥⎢⎢
⎥⎢⎢⎥⎢⎢
⎥⎢⎢
⎥⎢⎢⎥⎢⎢⎥⎢⎢
⎥⎢⎢
⎥⎢⎢⎥⎢⎢
⎥⎢⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢⎥⎢⎢
⎥⎢⎢
⎥⎢⎢⎥⎢
⎥⎢
⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎢
⎥⎢
⎥⎢⎥⎣⎦
∇∇∇11121321222331323300000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000010000000001C C C C C C C C C +⎤⎥
⎥
⎥
⎥
⎥⎥
⎥
⎥⎥
⎥
⎥⎥
⎥
⎥⎥
⎥
⎥⎥
⎥
⎥
⎥
⎥⎥⎥
⎥
⎥⎥
⎥
⎥⎥
⎥
⎥⎥⎥⎥
⎢⎥
⎢⎥
⎢⎥
⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎦
00000000010000000001000000000100
1gx gy gz bx by bz ax ay az ωωωωωωωωω⎡⎤
⎢⎥⎡
⎤⎢⎥⎢⎥
⎢⎥⎢⎥
⎢⎥⎢⎥⎢⎥⎢⎥
⎢⎥⎢⎥
⎢⎥⎢⎥
⎢⎥⎢⎥
⎢⎥⎢⎥⎢⎥⎢⎥
⎢⎥⎢⎥
⎢⎥⎢⎥⎢⎥⎢⎥
⎢⎥⎢⎥
⎢⎥⎢⎥⎢⎥⎢⎥
⎢⎥⎢⎥
⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥
⎢⎥⎢⎥
⎢⎥⎢⎥⎢⎥⎢⎥
⎢⎥⎣⎦
⎢⎥⎢⎥⎣⎦
Cij 为捷联矩阵t b C 的第i
行第j 列的元素; E f 为地理系下东向加表的比力,其它同理;
bx ε为陀螺的随机常值漂移,其它同理;
rx ε为一阶马尔柯夫随机过程,其它同理;
(表示陀螺的随机漂移,用一阶玛尔柯夫过程来描述) T
91
I gx
gy gz bx by bz ax ay az W ωωωωωωωωω⨯⎡⎤=⎣⎦
x ∇为加速度计的零偏;其它同理;
gx ω是由陀螺仪的刻度因数误差和安装误差角引起在载体坐标系X 轴的分量,其他同理;
(修改:经推导此处方程与《惯导原理》秦永元版本有区别,其中的Cij 矩阵有三个地方都需要取负号才正确)
000
1
11
11
1
rx bx
x
ry
by
y
rz bz z
x ax
x
ax y ay y
ay
z az z
az
bx by bz rx T ry T rz
T T T T εωε
ωεωωωωεεεεεε====-+=-+=-
+=-∇+=-∇+=-
∇+∇∇∇。
