第六章 捷联惯导
捷联式惯性导航系统培训讲学
1 绪论随着计算机和微电子技术的迅猛发展，利用计算机的强大解算和控制功能代替机电稳定系统成为可能。
于是，一种新型惯导系统--捷联惯导系统从20世纪60年代初开始发展起来，尤其在1969年，捷联惯导系统作为"阿波罗"-13号登月飞船的应急备份装置，在其服务舱发生爆炸时将飞船成功地引导到返回地球的轨道上时起到了决定性作用，成为捷联式惯导系统发展中的一个里程碑。
捷联式惯性导航(strap-down inertial navigation)，捷联（strap-down）的英语原义是“捆绑”的意思。
因此捷联式惯性导航也就是将惯性测量元件（陀螺仪和加速度计）直接装在飞行器、舰艇、导弹等需要诸如姿态、速度、航向等导航信息的主体上，用计算机把测量信号变换为导航参数的一种导航技术。
现代电子计算机技术的迅速发展为捷联式惯性导航系统创造了条件。
惯性导航系统是利用惯性敏感器、基准方向及最初的位置信息来确定运载体的方位、位置和速度的自主式航位推算导航系统。
在工作时不依赖外界信息，也不向外界辐射能量，不易受到干扰破坏。
它完全是依靠载体自身设备独立自主地进行导航，它与外界不发生任何光、声、磁、电的联系，从而实现了与外界条件隔绝的假想的“封闭”空间内实现精确导航。
所以它具有隐蔽性好，工作不受气象条件和人为的外界干扰等一系列的优点，这些优点使得惯性导航在航天、航空、航海和测量上都得到了广泛的运用[1]1.1 捷联惯导系统工作原理及特点惯导系统主要分为平台式惯导系统和捷联式惯导系统两大类。
惯导系统（INS）是一种不依赖于任何外部信息、也不向外部辐射能量的自主式导航系统，具有隐蔽性好，可在空中、地面、水下等各种复杂环境下工作的特点。
捷联惯导系统（SINS）是在平台式惯导系统基础上发展而来的，它是一种无框架系统，由三个速率陀螺、三个线加速度计和微型计算机组成。
平台式惯导系统和捷联式惯导系统的主要区别是：前者有实体的物理平台，陀螺和加速度计置于陀螺稳定的平台上，该平台跟踪导航坐标系，以实现速度和位置解算，姿态数据直接取自于平台的环架；后者的陀螺和加速度计直接固连在载体上作为测量基准，它不再采用机电平台，惯性平台的功能由计算机完成，即在计算机内建立一个数学平台取代机电平台的功能，其飞行器姿态数据通过计算机计算得到，故有时也称其为"数学平台"，这是捷联惯导系统区别于平台式惯导系统的根本点。
捷联惯性导航原理
2.捷联惯导力学编排方程
姿态角定义： ψ航向角----载体纵轴在水平面的投影与地理子午线之间 的夹角，用ψ表示，规定以地理北向为起点，偏东方向 为正，定义域0~360°。 θ俯仰角----载体纵轴与纵向水平轴之间的夹角，用θ表 示，规定以纵向水轴为起点，向上为正，向下为负，定 义域-90 ° ~+90 ° 。 γ横滚角----载体纵向对称面与纵向铅垂面之间的夹角， 用γ表示，规定从铅垂面算起，右倾为正，左倾为负， 定义域-180 ° ~+180° 。（载体纵向对称面和 纵轴空 间 铅垂面）
捷联惯性导航原理
2010.11.30 北航通信导航与自动测试实验室
如果载体真实地理位置以纬度、经度、高度 表示，则与此对应的载体在地球坐标系中的 真实位置(x，y，z)可通过下式求得:
地球各点重力加速度近似计算公式: g=g0(1-0.00265cos&)/1+(2h/R) g0:地球标准重力加速度9.80665(m/平方秒) &:测量点的地球纬度 h:测量点的海拔高度 R: 地球的平均半径(R=6370km) s:时间 ？？？？？？？？？？？？？？？？？？？？
f 为地球椭球模型的椭圆度，f= 1/298.257223563
R1 RN h R2 RM h
注意从瞬时速度过来那条线，用来计算w（enn）
3、捷联惯导系统的算法
3.1 姿态更新算法 四元数法：
Q(q0 , q1 , q2 , q3 ) q0 q1i q2 j q3k
1. 惯性导航中的常用坐标系
yt
yb
z e zi
北
xb
zb
zt
xt
O
东
Oe
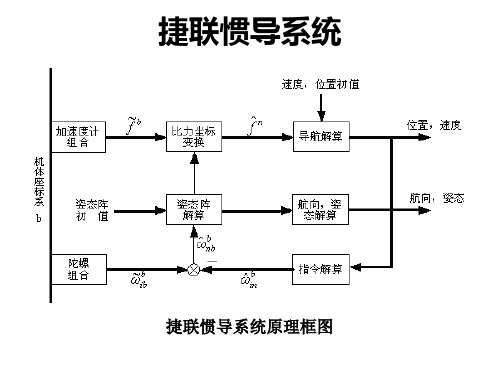
捷联惯导系统解读
Q cos
u sin
2(q1q2 q0 q3 )
2 2 q0 q12 q22 q3
2(q2 q3 q0 q1 )
2(q1q3 q0 q2 ) 2(q2 q3 q0 q1 ) 2 2 q0 q12 q2 q32
T11 T21 T31 C bn T T T 12 22 32 T13 T23 T33
1 sin (T32 ) T31 1 tan ( ) 主 T 33 1 T 主 tan ( 12 ) T22
b nb x b 0 nby b 1 cos tan nb z 0
cos cos sin
当 90 时，方程退化，故不能全姿态工作。
捷联惯导系统
2.2 方向余弦法（九参数法）
n C n ωbk C b b nb
0 [ G ] Gz Gy
Gz
0 Gx
Gy Gx 0
K x [ K ] 0 0
0
Ky
0
0 0 Kz
捷联惯导系统
捷联惯导系统误差方程
b b b n n ωnb ωib Cn Cnωin
矢量的方向余弦表示姿态矩阵的方法； 可全姿态工作，但需要解含有九个未知量的线性方程组，计算量大， 工程上不实用。
捷联惯导系统
2.3 四元数法（四参数法）
2.3.1 四元数基本概念 四元数是由一个实数单位1和一个虚数单位i、j、k组成的含有四个 元的数。（超复数） Q q0 , q1, q2 , q3 q0 q1i q2 j q3k 四元数的大小——范数
捷联惯导算法与组合导航原理讲义
捷联惯导算法与组合导航原理讲义一、捷联惯导算法捷联惯导（Inertial Navigation System，INS）是一种通过测量惯性传感器的运动参数实现导航定位的技术。
惯性导航系统中包括了加速度计和陀螺仪等传感器，通过测量物体的加速度和角速度，可以推算出物体的位置、速度和姿态等信息。
1.1加速度计加速度计是一种测量物体加速度的传感器。
常见的加速度计有基于压电效应的传感器和基于微机电系统（Microelectromechanical System，MEMS）的传感器。
加速度计的原理是通过测量物体受到的惯性力，推算出物体的加速度。
由于加速度是速度对时间的导数，因此通过对加速度的积分操作，可以计算出物体的速度和位移。
1.2陀螺仪陀螺仪是一种测量物体角速度的传感器。
常见的陀螺仪有机械陀螺仪和MEMS陀螺仪等。
陀螺仪的原理是基于角动量守恒定律，通过测量转动惯量的变化，推算出物体的角速度。
与加速度计类似，通过对角速度的积分操作，可以计算物体的姿态。
1.3捷联惯导算法离散时间模型中，位置、速度和姿态等状态变量通过积分加速度和角速度来更新。
由于加速度计和陀螺仪测量结果存在噪声，因此在积分操作时需要加入误差补偿算法来消除误差。
常见的误差补偿算法有零偏校正和比例积分修正等。
连续时间模型中，位置、速度和姿态等状态变量通过微分方程来描述，并通过求解微分方程来更新状态。
由于计算量较大，通常需要使用数值积分方法来求解微分方程。
常见的数值积分方法有欧拉法、中点法和四阶龙格-库塔法等。
二、组合导航原理组合导航是一种融合多种导航技术的导航方式。
常见的组合导航方式有捷联惯导与GPS组合导航。
组合导航通过融合多种导航系统的测量结果，可以提高导航定位的精度和可靠性。
2.1捷联惯导与GPS组合导航捷联惯导与GPS组合导航是一种常见的组合导航方式。
在这种方式下，捷联惯导提供了高频率的惯导数据，可以提供较高的定位精度，但是由于其测量结果累积误差较大，会逐渐偏离真实轨迹。
车载捷联惯导系统基本原理
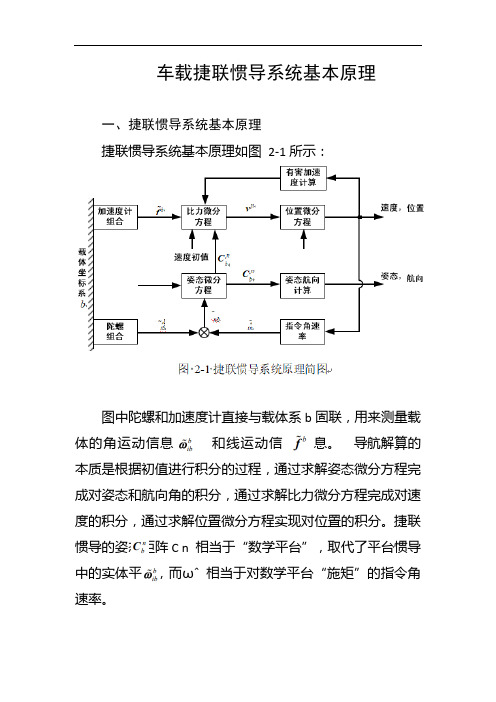
车载捷联惯导系统基本原理一、捷联惯导系统基本原理捷联惯导系统基本原理如图2-1所示：图中陀螺和加速度计直接与载体系b固联，用来测量载体的角运动信息和线运动信息。
导航解算的本质是根据初值进行积分的过程，通过求解姿态微分方程完成对姿态和航向角的积分，通过求解比力微分方程完成对速度的积分，通过求解位置微分方程实现对位置的积分。
捷联惯导的姿态矩阵C n 相当于“数学平台”，取代了平台惯导中的实体平台，而ωˆ相当于对数学平台“施矩”的指令角速率。
二、捷联惯导微分方程（一）姿态微分方程在捷联惯导系统中，导航坐标系n 和载体坐标系b 之间的角位置关系通常用姿态矩阵、四元数和欧拉角表示，相应也存在姿态矩阵微分方程、四元数微分方程和欧拉角微分方程三种形式。
姿态矩阵微分方程的表达式为：在欧拉角微分方程式(2.2-7)中，当俯仰角θ趋于90º时，cosθ趋于0，tanθ趋于无穷，方程存在奇异性，所以这种方法不能在全姿态范围内正常工作；姿态矩阵微分方程式(2.2-1)可全姿态工作，但姿态矩阵更新相当于求解包含9个未知量的线性微分方程组，计算量大；四元数微分方程式(2.2-6)同样可以全姿态工作，且更新算法只需求解4个未知量的线性微分方程组，计算量小，算法简单，是较实用的工程算法。
（二）速度微分方程速度微分方程即比力方程，是惯性导航解算的基本关系式：三、捷联惯性导航算法捷联惯导解算的目的是根据惯性器件输出求解载体姿态、速度和位置等导航信息，实际上就是求解三个微分方程的过程，相应存在姿态更新算法、速度更新算法和位置更新算法。
（一）姿态更新算法求解微分方程式(2.2-6)可得四元数姿态更新算法为：在车辆行驶过程中，一般不存在高频大机动环境，并且车载导航系统往往不工作在纯惯性导航方式，而是利用里程仪或零速条件进行组合导航，所以算法误差的影响有限，常用的5ms采样周期和二子样优化算法即可满足要求。
四、捷联惯导误差模型传感器误差、初值误差和算法误差是SINS的主要误差源，其中器件误差和初值误差又是影响导航结果的主要因素。
捷联惯导
坐标系的定义
1. 地理坐标系（下标为t）—— OXtYtZt ：O 取载体质心，Xt 轴指向东，Yt 轴指向北，Zt 轴沿垂线指向天。 2. 导航坐标系（下标为n）—— OX nYnZn ：O 取载体质心，Zn与 Zt 重合，Xn 与 Xt，Yn 与 Yt 相差一个游动方
C13
C23
C33
位置速率
p ep
位置速率是由飞行器地速的水平分量引起的，由于平台坐标系与地理坐标系相差 一个游动方位角，
可得：
VVENtt
cos sin
sin cos
VEp VNp
p ep
可写成
p epE
C32 C31
180 ,180
1.求纬度的真值L
L L 反正弦函数的主值域与L的定义域一致，因此：
主
2.求经度的真值
反正切函数的主值域是 90 ,90 与 的定义域不一致，因此需要在 的定义域内确定经度的真值。
由： 主
tan 1
C32 C31
tan 1
cos L sin cos L cos
其中：
.
V ep 平台系相对地球的加速度向量
f 加速度计测量的比力向量
2ie ep V ep 无明显物理意义，又称有害加速度
g 重力加速度向量
整理上式可得：
.
VEp
.
VNp
.
VUp
f
p E
捷联惯导结算原理
0 cos sin ， Rz sin 0 cos
sin cos 0
0 0 1
cos cos sin sin sin cos cos sin sin cos sin cos T11 T12 T13 Ry Rx Rz cos sin cos cos sin T21 T22 T23 sin cos cos sin sin sin sin cos sin cos cos cos T T T 31 32 33 b 由姿态矩阵 C n 反解飞行器姿态欧拉角：
（5） 速度的计算
t t t t t 0 2iez etz ety 2iey Vxt Vx 0 t t b t t t t 0 2iex etx Vyt 0 Vy Cb f 2iez etz t Vz g Vzt 2 t t 2 t t 0 iey ety iex etx
o o sin 1 T23 , 90 , 90
tg 1
T13 180o , 180o , T33
tg 1
T21 o o , 180 , 180 T 22
图 6 东向北向速度变化曲线
阶段总结：1.学习了平台式和捷联式惯导的惯导解算方法并进行了仿真计算。 2.平台式惯导物理平台时刻跟踪当地水平东北天地理系， 加速计的比 力信息直接投影在导航系中，可直接进行导航速度和位置解算。载体的姿态可直 接从平台框架直接得出；而捷联式惯导用数学平台取代实体的物理平台，通过求
捷联惯导系统设计和分析
1 概述
本文将简略讨论捷联惯导系统设计。 尽管不同的应用中所采用的具体方法和设计重点常 常很不相同，但对任何捷联系统，一般都需要下面的设计步骤。 对于应用于战术导弹上的捷联惯导系统， 应重点评估和分析惯导系统在动态飞行条件下 的性能。惯导系统将受飞行机动、大加速度和恶劣的振动环境的影响，所有这些都将大大影 响惯性器件的选择以及它们在飞行中能够提供的测量精度。 另外， 从运动平台上发射的导弹 也会影响导弹反射前进行的导航初始对准精度。因此，在整个系统设计过程中，对影响系统 性能的所有可能的误差源之间进行合理的平衡折中非常重要。 作为系统设计过程的一部分，必须首先考虑选择对应用最合适的系统机械编排。然后， 通过误差预估分析评估可接受的对准误差、 惯性器件误差和导航解算误差的大小。 误差预估 要求的评估可在不同的水平上进行， 从相对简单的单通道误差模型到应用仿真进行更严格的 分析， 其中后者可以考虑到动态运动的影响进而进行更精确的评估。 对于此处讨论的战术导 弹应用，动态影响较大，简化的计算很难适用，因此，需采用更复杂的计算，或更常用的误 差预估分配仿真。一般地，在确定既实际又可行的一组误差参数值之前，需要误差预估分析 过程的几次迭代。 在确定了惯性器件工作特性和对准精度以及任何可能潜在的计算困难后， 就可以开始确 定适用的惯性器件以及导航解算算法。 在这个过程中， 可能需要根据惯性器件的类型对误差 预估计算进行更多的迭代，以得到更满意的设计。
以损失一个参数为代价而放宽另一些参数对误差预估的影响的做法， 其作用通常相当有 限。例如，在基于常规陀螺的设计中，固定零偏项对误差预估的影响允许增加一些，而将与
g 有关的零偏调整到在实际应用中更容易实现的水平。分析表明，在这类的应用中系统性能
对与 g 有关的零偏系数特别敏感。同时还可见，与陀螺仪和加速度计有关的某些交叉耦合项 需要为小量，以便达到所需的性能。 当然无论什么时候都应确保任何一项误差的影响都不会超过总误差预估。 通常需要对参 数选择过程进行几次迭代， 才能获得一组合理的设置值。 表 2 给出了一组误差参数值以及它 们各自对总位置和姿态误差预估的影响。 表 2 清楚地表明， 主要的误差源是姿态对准误差以及某些与 g 有关的陀螺零偏和加速度 计交叉耦合，在导弹存在纵向加速度时后两者会引起较大的位置误差。此外，在导弹飞行的 助推阶段有俯仰转弯机动时，陀螺交叉耦合误差对总误差预估也产生显著影响。 利用表 2 给出的对准误差和惯性器件误差， 沿航迹的位置误差、 横滚误差和速度误差 （在 该表没有给出）可计算： 1) 沿航迹位置误差 RSS 41m ； 2) 横滚误差 RSS 0.3 ； 3) 沿航迹速度误差 RSS 0.7 m s ； 4) 横向速度误差 RSS 3.7 m s ； 5) 垂直速度误差 RSS 3.8 m s 。 由上述误差可知，每项都在技术指标要求规定的范围内。 确定了惯性器件的性能指标之后， 重要的是评估在一组典型弹道上的系统性能。 许多误 差对总导航性能的影响， 常常与飞行期间系统承受的精确运动密切相关。 为了更好地设计系 统，在设计阶段可能需要进一步细化某些误差参数值。 在按上述的过程设计时，设计可能希望把某些误差合并，尤其是那些传播方式类似，对 惯导系统性能的影响类似的误差。例如： 1) 陀螺仪非等弹性:当存在周期运动时，由于轴承变形不相等，在常规陀螺仪输出中会造 成零偏。 2) 加速度计振摆误差：当存在振动时，在摆式加速度计输出中会存在附加的零偏。 3) 圆锥和划桨运动： 如果惯性器件处于圆锥和划桨运动状态， 会分别出现附加的角速率和 线加速度零偏。 为了考虑这些影响，在误差预估分析中所采用的陀螺仪和加速度计零偏可能需要增加。
捷联惯导与组合导航技术
1
捷联式惯性导航
• 1.1 捷联惯导简介
捷联惯性导航系统是把惯性传感器直接固 连在载体上，用计算机来完成平台惯性导航中 的惯性平台功能的惯性导航系统。由于惯性传 感器直接固连在载体上，省去了机电式的惯性
平台，从而给系统带来了优点：
• 1.省去了惯性平台，整个系统的体积、质量 和成本大大降低； • 2.惯性仪表便于安装维护，也便于更换； • 3.惯性仪表可以给出载体轴向的线加速度和 角加速度，这些信息也是控制系统所需要 的。
• 对于捷联惯性导航系统，由于计算误差、不可交 换性误差等影响，会使四元数逐渐失去规范性， 即范数不再等于1，所以应对计算的四元数进行周 期性的最佳规范化处理。规范化的周期通常取为 捷联矩阵即时解算周期r的整数倍。具体规范化方 法如下：
• • 表示规范化后的四元数元素 表示计算得到的四元数元素
• 通过规范化后的四元数各元素，根据四元 数与姿态阵的关系可求得捷联矩阵
• 3.平台惯性导航系统的陀螺仪安装在平台上， 可以相对重力加速度和地球自转角速度任意 定向来进行测试，便于误差标定。而捷联陀 螺仪不具备这个条件，因为装机标定比较困 难，从而要求捷联陀螺有更高的参数稳定性。
• 1.2 捷联式惯导的姿态解算方法
• 关于姿态解算最为常用的方法有欧拉角法、 四元数法、等效旋转矢量法、罗德里格参 数法、方向余弦矩阵法。从本质上看，罗 德里格参数法和四元数法是一种方法，欧 拉角法和方向余弦矩阵是一种方法。所以， 本质上解算姿态的方法就3种：方向余弦矩 阵、等效旋转矢量、四元数。
我们研究的组合导航
• SlNS／DGPS／视觉／数字地图组合导航 技术 • GPS与SINS形成的位置与姿态观测信息， 机器视觉／数字地图／SINS形成的横向偏 信息
（精品）捷联式惯性导航系统
1 绪论00随着计算机和微电子技术的迅猛发展，利用计算机的强大解算和控制功能代替机电稳定系统成为可能。
于是，一种新型惯导系统--捷联惯导系统从20世纪60年代初开始发展起来，尤其在1969年，捷联惯导系统作为"阿波罗"-13号登月飞船的应急备份装置，在其服务舱发生爆炸时将飞船成功地引导到返回地球的轨道上时起到了决定性作用，成为捷联式惯导系统发展中的一个里程碑。
00捷联式惯性导航(strap-down inertial navigation)，捷联（strap-down）的英语原义是“捆绑”的意思。
因此捷联式惯性导航也就是将惯性测量元件（陀螺仪和加速度计）直接装在飞行器、舰艇、导弹等需要诸如姿态、速度、航向等导航信息的主体上，用计算机把测量信号变换为导航参数的一种导航技术。
现代电子计算机技术的迅速发展为捷联式惯性导航系统创造了条件。
惯性导航系统是利用惯性敏感器、基准方向及最初的位置信息来确定运载体的方位、位置和速度的自主式航位推算导航系统。
在工作时不依赖外界信息，也不向外界辐射能量，不易受到干扰破坏。
它完全是依靠载体自身设备独立自主地进行导航，它与外界不发生任何光、声、磁、电的联系，从而实现了与外界条件隔绝的假想的“封闭”空间内实现精确导航。
所以它具有隐蔽性好，工作不受气象条件和人为的外界干扰等一系列的优点，这些优点使得惯性导航在航天、航空、航海和测量上都得到了广泛的运用[1]001.1 捷联惯导系统工作原理及特点惯导系统主要分为平台式惯导系统和捷联式惯导系统两大类。
惯导系统（INS）是一种不依赖于任何外部信息、也不向外部辐射能量的自主式导航系统，具有隐蔽性好，可在空中、地面、水下等各种复杂环境下工作的特点。
捷联惯导系统（SINS）是在平台式惯导系统基础上发展而来的，它是一种无框架系统，由三个速率陀螺、三个线加速度计和微型计算机组成。
平台式惯导系统和捷联式惯导系统的主要区别是：前者有实体的物理平台，陀螺和加速度计置于陀螺稳定的平台上，该平台跟踪导航坐标系，以实现速度和位置解算，姿态数据直接取自于平台的环架；后者的陀螺和加速度计直接固连在载体上作为测量基准，它不再采用机电平台，惯性平台的功能由计算机完成，即在计算机内建立一个数学平台取代机电平台的功能，其飞行器姿态数据通过计算机计算得到，故有时也称其为"数学平台"，这是捷联惯导系统区别于平台式惯导系统的根本点。
《2024年捷联惯性导航系统关键技术研究》范文
《捷联惯性导航系统关键技术研究》篇一一、引言随着科技的进步，导航系统在众多领域如航空、航天、机器人等领域扮演着至关重要的角色。
其中，捷联惯性导航系统（Inertial Navigation System，简称INS）因其具有独立性强、实时性高和隐蔽性好的特点，成为众多导航系统中重要的技术手段。
本文旨在探讨捷联惯性导航系统的关键技术及其发展趋势。
二、捷联惯性导航系统概述捷联惯性导航系统基于惯性传感器（如陀螺仪和加速度计）的测量原理，将物理信息转化为电信号，以实现对载体姿态、速度和位置的实时解算。
相较于传统的平台式惯性导航系统，捷联式结构更加简单、体积更小、可靠性更高。
三、关键技术研究1. 惯性传感器技术惯性传感器是捷联惯性导航系统的核心部件，其性能直接决定了系统的精度和稳定性。
目前，高精度、低噪声的陀螺仪和加速度计是研究的重点。
此外，微机电系统（MEMS）技术的发展为惯性传感器的小型化、低成本化提供了可能。
2. 算法研究算法是捷联惯性导航系统的灵魂，其性能直接影响到系统的解算精度和实时性。
目前，主要的算法包括姿态解算算法、速度和位置解算算法、误差补偿算法等。
其中，基于卡尔曼滤波的姿态和位置解算算法是研究的热点。
此外，随着人工智能技术的发展，基于深度学习、神经网络的算法也在逐渐应用于捷联惯性导航系统中。
3. 系统集成与优化系统集成与优化是提高捷联惯性导航系统性能的重要手段。
这包括硬件电路的优化设计、软件算法的优化以及系统整体性能的评估与优化等。
通过优化设计，可以在保证系统性能的前提下，减小系统的体积和成本，提高系统的可靠性。
四、发展趋势1. 高精度化：随着科技的进步，对导航系统的精度要求越来越高。
因此，进一步提高惯性传感器的精度、优化算法、减少误差等是未来的重要研究方向。
2. 智能化：随着人工智能技术的发展，将人工智能技术应用于捷联惯性导航系统中，提高系统的自主性、智能性和适应性是未来的重要趋势。
3. 微型化：随着微机电系统（MEMS）技术的发展，捷联惯性导航系统的微型化、低成本化将成为可能。
《2024年捷联惯性导航系统关键技术研究》范文
《捷联惯性导航系统关键技术研究》篇一一、引言捷联惯性导航系统（SINS）是现代导航技术的重要组成部分，其核心利用惯性测量单元（IMU）来感知和测量载体的运动状态，从而实现对载体的导航和定位。
随着科技的不断进步，SINS在军事、民用等领域的应用越来越广泛，对其关键技术的研究也日益深入。
本文将重点探讨捷联惯性导航系统的关键技术研究，以期为相关领域的研究和应用提供参考。
二、SINS的基本原理与构成SINS主要由惯性测量单元（IMU）、导航算法和数据处理模块等部分构成。
其中，IMU是SINS的核心部件，包括加速度计和陀螺仪等传感器，用于测量载体的运动状态。
导航算法则根据IMU测量的数据，通过一定的算法计算出载体的姿态、速度和位置等信息。
数据处理模块则负责对导航算法输出的数据进行处理和优化，以提高导航精度和稳定性。
三、SINS的关键技术研究1. IMU技术研究IMU是SINS的核心部件，其性能直接影响到SINS的导航精度和稳定性。
因此，IMU技术的研究是SINS关键技术研究的重点。
目前，IMU技术的研究主要集中在提高传感器的精度、降低噪声、增强抗干扰能力等方面。
此外，多传感器融合技术也是IMU技术研究的热点，通过将多种传感器数据进行融合，可以提高SINS的导航精度和稳定性。
2. 导航算法研究导航算法是SINS的核心，其性能直接影响到SINS的导航精度和响应速度。
目前，常用的SINS导航算法包括经典的最小二乘法、卡尔曼滤波算法等。
然而，这些算法在复杂环境下的性能受到限制。
因此，研究新型的、适用于复杂环境的SINS导航算法具有重要意义。
例如，基于神经网络的导航算法、基于深度学习的导航算法等都是当前研究的热点。
3. 数据处理与优化技术研究数据处理与优化技术是提高SINS性能的重要手段。
通过对导航算法输出的数据进行处理和优化，可以提高SINS的导航精度和稳定性。
目前，常用的数据处理与优化技术包括数据滤波、数据融合、误差补偿等。
捷联惯性导航总结
z
0 x
y
姿态矩阵计算方法
3 四元数微分方程及其解
1 qk 1 exp( )qk Mq k qk rk 2
rk ac as x i as y j as z k
(0.5 )2 (0.5 )4 ac cos( ) 1 2 2! 4!
tk b nb
t
v f dt
b tk
t
速度微分方程求解
2 速度积分算法
v f dt [2ω ωen ] v dt g1 dt
n n 0 0 n ie n n n 0
t
t
t
v
n k 1
v u gt
n k n
b
v
n l 1
[ I 2Ωie tl Ωen tl ]v
v f dt
b
t
1 tk 1 αk 1 α ωdt 2 tk
α ωdt
tk
tk
t
捷联导航算法
捷联惯导误差分析
主要误差源
1 初始对准误差
2 惯性器件误差
3 计算误差
误差传播方程：误差源与系统性能的相互关系的 方程，主要用来阐述各种类型误差随时间的传播 过程。
捷联惯导误差分析
sin( / 2) (0.5 ) (0.5 ) as 0.5(1 ) 3! 5!
2 4
姿态矩阵计算方法
4 圆锥误差
σ αk 1 αk 1
α ωdt
tk t
1 tk 1 αk 1 α ωdt 2 tk
姿态矩阵计算方法
5 姿态角计算
b nbz
6.7 捷联式惯性导航系统
rx0 cos H ry0 sin H rx0 sin H ry0 cos H
rz1 rz0
cos H sin H 0
TheFirstTurn : sin H cos H 0
0
0 1
rx0
H x0
x1（ x2）
ry1
O
ry0
rx1
θ y1
3
捷联式惯性导航系统
捷联姿态矩阵
地理坐标系 ox0y0z0 与载体坐标系 oxyz 之间的关系，可以用三个转动欧 拉角来表示：
z
z2
Ф
z0(z1)
θ
o
ox0 y0z0
绕oz0
H
ox1 y1z1
绕ox1
ox2 y2z2
绕oy2
oxyz
H
x0
Ф
x1(x2) x
y2(y)
θ y1
H
y0
捷联式惯性导航系统
sin cos
cos sin H cos cos H
sin
sin cos H cos sin sin H
sin
sin
H
cos
sin
cos
H
cos cos
作用1：姿态和航向的求解
z
z2
Ф
z0(z1)
θ
tg 1
T31 T33
sin
sin
H
cos
sin
cos
H
cos cos
• 纵摇角—— θ • 横摇角—— • 航向角—— H
捷联惯导系统
（3）无框架锁定系统，允许全方位（全姿态）工作。
（4）除能提供平台式系统所能提供的所有参数外，还可以提供沿弹 体三个轴的速度和加速度信息。
缺点：
但是，由于在捷联惯导系统中，惯性元件与载体直接固连， 其工作环境恶劣，对惯性元件及机（弹）载计算机等部件也 提出了较高的要求。
（1）要求加速度表在宽动态范围内具有高性能、高可靠性， 且能数字输出。
1.4捷联惯导系统的精度
惯性导航和制导系统对陀螺仪和加速度计的精度要求极高， 如加速度计分辨率通常为0.0001g～0.00001g，陀螺随机漂 移率为0.01°/小时甚至更低，并且要求其有大的测量范围， 如军用飞机所要求的测速范围应达10的9次方（0.01°/小 时～400°/秒）。因此，陀螺仪和加速度计属于精密仪表范 畴。
“数学解析平台”的原理简图
捷联惯导优点：
捷联惯导系统和平台式惯导系统一样，能精确提供载体的姿态、地 速、经纬度等导航参数。但平台式惯导系统结构较复杂、可靠性较 低、故障间隔时间较短、造价较高，为可靠起见，通常在一个运载 体上要配用两套惯导装臵，这就增加了维修和购臵费用。在捷联惯 导系统中，由于计算机中存储的方向余弦解析参考系取代了平台系 统以物理形式实现的参考系，因此，捷联惯导系统有以下独特优点。 （1）去掉了复杂的平台机械系统，系统结构极为简单，减小了系统 的体积和重量，同时降低了成本，简化了维修，提高了可靠性。 （2）无常用的机械平台，缩短了整个系统的启动准备时间，也消除 了与平台系统有关的误差。
为测量基准，它不再采用机电平台，惯性平台的功能由计算 机完成，即在计算机内建立一个数学平台取代机电平台的功 能，其飞行器姿态数据通过计算机计算得到，故有时也称其 为"数学平台"，这是捷联惯导系统区别于平台式惯导系统的 根本点。由于惯性元器件有固定漂移率，会造成导航误差， 因此，远程导弹、飞机等武器平台通常采用指令、GPS或其 组合等方式对惯导进行定时修正，以获取持续准确的位臵参 数。如采用指令+捷联式惯导、GPS+惯导（GPS/INS）。美国 的战斧巡航导弹采用了GPS+INS +地形匹配组合导航。
第六章 惯性导航系统的对准
初始对准的目标：精度高，时间短。在尽可能短的 时间内达到最高的对准精度，是捷联惯导初始对准 技术所追求的目标。捷联惯导的初始对准就是确定 初始时刻的姿态矩阵，即数学平台。
6.1 基本原理
捷联惯性导航系统的初始对准分类：
按照对准阶段来分，初始对准一般分为:
第一阶段为粗对准;捷联系统粗对准的任务是得到粗略的捷
联矩阵，为后续的精对准提供基础，此阶段精度可以低一些， 但要求速度快; 第二阶段为精对准。精对准是在粗对准的基础上进行的， 通过处理惯性敏感元件的输出信息，精确校正计算的导航坐 标系与理想导航坐标系之间的失准角，使之趋于零，从而得 到精确的捷联矩分，可以分为静基 座对准和动基座对准。静基座对准时运载体是不动的， 而动基座对准是在运载体运动状态下完成的。 按照初始对准时是否取得外部信息，可以分为自对 准和非自对准。自对准是利用重力矢量和地球自转角 速率矢量通过解析的方法实现的初始对准，这种对准 方法的优是自主性强，缺点是所需的对准时间长。非 自主式对准可以通过机电或光学方法将外部参考信息 引入系统，实现惯性系统的初始对准。
第六章 惯性导航系统的对准
6.1 6.2 6.3 6.4 基本原理 地面对准 空中对准 海上的对准
6.1 基本原理
对准：确定惯性导航系统中各坐标轴相对于参考坐 标系指向的过程。 对准过程的类型：利用陀螺罗经的自对准 子系统相对基准的对准
对准过程主要是确定由加速度计轴定义的直角坐标 系相对于给定的参考坐标的指向角
6.1 基本原理
捷联系统初始对准首先是利用外部信息或由惯性测量组件提供 的信息粗略地确定出捷联矩阵。由于没有考虑到惯性测量元件 的测量误差等的影响，这时给出的捷联矩阵与真实的捷联矩阵 之间存在误差，相应于实际的地理系与理想的地理系之间存在 失准角，造成加速度计测量的比力经过捷联矩阵转换后在地理 坐标系的水平方向有分量。初始对准就是应用这个信息来不断 地估计水平失准角 的。 当数学解析平台有方位失准角 时，则地球自转角速率分 量。 . 就藕合到解析平台的东轴上，就使数学解析 平台绕东西轴旋转，从而产生水平倾角 。为了使解析平台 保持水平，必须在东西轴上加一个控制信号，从而使数学解析 平台稳定在地理坐标系上。
惯导原理捷联惯导基本算法与误差课件
由于陀螺仪和加速度计随时间变 化的稳定性问题导致的偏差，这 种误差通常需要通过实时滤波和 数据融合技术来减小。
05
提高捷联惯性导航精度的策
略
采用高性能的惯性传感器
陀螺仪
陀螺仪是惯性导航系统中的重要组成部分，能够测量载体在三个轴向的角速度。 采用高性能的陀螺仪可以提高捷联惯性导航系统的精度。
粒子滤波是一种基于贝叶斯推断的非线性滤波算法，能够处理非线性、非高斯系统。采用粒子滤波可以提高捷联 惯性导航系统在复杂环境下的性能。
利用外部信息进行修正
GPS修正
全球定位系统（GPS）是一种高精度的导航系统，能够提供准确的位置和时间信息。利用GPS信息对 捷联惯性导航系统进行修正可以提高其精度。
无线通信修正
利用无线通信网络，接收外部信息对捷联惯性导航系统进行修正可以提高其精度。例如，接收差分 GPS信号、无线电导航信号等。
06
捷联惯性导航发展趋势与挑
战
技术升级与改进
器件性能提升
随着微电子、精密制造等技术的 进步，捷联惯性导航系统的器件 性能得到不断提升，为实现更高
精度的导航提供了基础保障。
算法优化
04
捷联惯性导航误差分析
系统误差
零偏误差
由于陀螺仪和加速度计的 制造和安装偏差导致的固 定偏差，这种误差通常很 难通过校准消除。
刻度系数偏差
由于陀螺仪和加速度计的 刻度系数不准确导致的误 差，需要通过校准消除。
安装误差
由于陀螺仪和加速度计在 系统中的安装位置不准确 导致的误差，这种误差通 常很难通过校准消除。
随机误差
陀螺仪随机漂移误差
由于陀螺仪内部的热噪声和机械噪声导致的随机偏差，这种误差通常需要通过 滤波和数据融合技术来减小。
捷联惯导
G 格网航向角， 俯仰角， 倾斜角 ＝ G , 取＝0,所以 ＝ G
得到矩阵T后，沿机体坐标系测量的比力就可以转换到平台坐标系上，得到：
f T f
p
b
由姿态矩阵T确定飞行器姿态角
根据矩阵T中的元素可以确定各角的主值：
主＝sin 1 T32
T31 主＝ tan T33 1 T12 G主 tan T 22
t VEt、VN 地理坐标系下的东向和北向速度
方向余弦矩阵（位置矩阵）Ce
平台坐标系与地球坐标系转动关系为：
p
Xp Xe p Y C Y p e e Z Z e p
其中
C11 C12 C13 sin sin L cos cos sin sin sin L sin cos cos sin cos L Cep C21 C22 C23 cos sin L cos sin sin cos sin L sin sin cos cos cos L C C C33 cos L cos cos L sin sin L 32 31
C32 cos L sin tan 1 C31 cos L cos
由于在L的定义域内cosL永远为正，所以 cos 与C31同号
利用 C31，主 的正负值可确定真值 ：
主 = 主 180 主 180
C31 0 C31 0, 主 0 C31 0, 主 0
T11 T12 T13 cos cos G sin sin sin G cos sin G cos cos G cos sin sin G T T21 T22 T23 cos sin G sin sin cos G cos cos G sin sin G cos sin cos G T T T sin cos sin cos cos 31 32 33
捷联惯导与组合导航解读
3）惯性仪表的校准，对陀螺的标度系数进行测 定，对陀螺的漂移进行测定并补偿，对加速度 计也同样测定标度系数并存入计算机。初始过 程中对惯性仪表的校准是提高系统精度的重要 保证，相关内容在第五章中已有详细讨论。
3、惯性仪表的误差补偿，对捷联式惯导系统来说， 由于惯性仪表直接安装在机体上，因此，飞行 器的线运动和角运动都引起较大的误差，为了 保证系统的精度，必须对惯性仪表的误差进行 补偿，最好的补偿方法是计算补偿，一般通过 专用的软件来实现误差补偿，相关内容在第五 章中已有详细讨论。
? 1.3.1 四元数的基本概念
? 四元数是由一个实数单位 1和一个虚数单位 i、j、k 组成的含有四个元的数，其形式为：
Q? (q0,q1,q2,q3) ? q0 ? q1i ? q2 j ? q3k ? q0 ? q
? 我们知道，在平面问题中，一个复数 以表示二维空间中的一个矢量：
Z ? z1 ? jz2可
? 2）利用陀螺输出角速率信号，通过求解 四元数微分方程实时更新姿态矩阵：
四 元
q?(t)
?
1 q(t) ? ?
2
b
数 微 分 方 程
?q?0 ? ?0
??q?1 ?? ???qq??32 ???
?
1 ??? 2 ??
?
??
bx by bz
? ? bx
0
? ? bz ? by
? ? by ? bz
cos ? 0
2
sin ? 0
2
cos ? 0
2
cos ? 0
?
sin ? 0
?
sin
0
22
?
?
sin
0
?
sin
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第六章捷联惯导6-1捷联惯导的原理¾捷联惯导系统概述•捷联惯性技术的发展过程•捷联惯导系统与平台惯导系统的对比¾捷联惯导系统的基本力学编排方程•捷联惯导系统的算法概述•捷联惯导系统原理框图的说明•姿态方程的解算（1）姿态和航向角的计算（2）姿态矩阵的微分方程（3）四元数的运动学微分方程（4）等效旋转矢量法及其微分方程（5）位移角速率方程（6）速度方程•导航位置方程（1）游动方位系与地球系之间的方向余弦矩阵（2）载体位置计算（3）方向余弦矩阵计算•垂直通道阻尼¾捷联惯性器件的余度技术•单自由度陀螺仪的配置方案（1）四陀螺仪配置方案（2）六陀螺仪系统•二自由度陀螺仪的配置方案¾捷联惯导的数值计算方法•数值积分法（1）欧拉法（2）四阶龙格－库塔法•角速率信息的提取“捷联（Strapdown）”这一术语的英文原义就是“捆绑”的意思。
因此，所谓捷联惯性系统也就是将惯性敏感元件（陀螺与加速度计）直接“捆绑”在载体上，从而完成制导和导航任务的系统。
V-2导弹“阿波罗-13”宇宙飞船“海盗”火星降落器从捷联技术的发展过程中我们已经看到捷联系统的优越性已越来越突出的显示出来，并在许多方面已日渐代替平台系统。
为什么会出现这种情况呢？为了回答这一问题，这里从生产与使用的角度将捷联系统与平台系统做一对比。
（1）硬件和软件的复杂程度由于捷联系统没有平台框架及相连的伺服装置，因而简化了硬件；代价是增加了计算机的负担，需要一个比较复杂的实时程序。
（2）可靠性捷联系统的可靠性要比平台系统高，其原因是它的机械构件少，加之容易采用多敏感元件配置，实现余度技术。
（3）成本与可维护性由于平台系统在机械结构上要复杂得多，而对于捷联系统只是算法复杂些，因而从制造成本上看捷联系统的成本要比平台系统低。
从市场供应的情况来看，数字计算机的价格一直在下降，而平台系统的价格一直在上升。
此外，捷联系统比平台系统具有较长的平均故障间隔时间，加之模块设计简化了维修，从而捷联系统的可维护性比平台系统大为提高了。
（4）初始对准精度与系统精度决定系统精度的重要因素之一是惯导系统的初始基准建立的准确性。
平台系统的陀螺安装在台体上以后还可以相对重力加速度和地球自转轴方向任意定位，还可以根据需要标定惯性敏感元件的误差；而捷联系统的敏感元件在载体上安装以后就不能再标定，因此要求捷联敏感元件有较高的参数稳定性。
在系统的精度方面，由于捷联系统是靠计算机来实现“平台”作用的，所以其算法误差比平台系统要大些。
一般要求软件误差不应超过系统误差的10%。
此外，由于捷联敏感元件工作在较恶劣的动态环境（如高角速率等）中，捷联系统往往存在着不可忽视的动态误差。
（5）参与系统综合的能力捷联系统可以提供载体所要求的全部惯性基准信号，特别是可以直接给出载体的角速率，而平台系统则无法直接给出。
至于载体的姿态捷联系统可以很高的速率和精度以数字形式提供，而平台系统则是通过框架间安装的同步器获得的，而且还需要把它们分解到机体轴上。
同样，加速度信息也要分解到机体轴上。
这样就会带来传递误差。
因而，从姿态和加速度信息的精度和完整性上来看，捷联系统要比平台系统优越。
捷联系统还可以采用共同的惯性元件来执行多项任务，即具有较强的参与系统综合的能力。
综上所述可以看出，捷联系统与平台系统相比，就可靠性、体积、重量和成本而言，前者优于后者；就精度而言，后者优于前者，由于飞船、战术导弹及飞机的惯导系统具有中等精度与低成本的要求，所以采用捷联方案是十分适宜的。
启动自检测初始化姿态矩阵计算迭代次数导航计算控制信息计算结束N OY E S图6-1-1 捷联式惯导系统流程图所谓“捷联惯导算法”是指从惯性仪表的输出到给出需要的导航和控制信息所必须进行的全部计算问题的计算方法。
计算的内容和要求，根据捷联式惯导的应用或功能要求的不同有很大差别。
一般说来，有下面几个方面的基本内容。
最重要的一部分(1)系统的初始化(2)惯性仪表的误差补偿(3)姿态矩阵的计算(4)导航计算(5)导航和控制信息的提取由于载体的姿态是不断改变的，因此，姿态矩阵的元素是时间的函数。
为随时定出载体的姿态，当用四元数方法确定姿态矩阵时，应解一个四元数的运动学方程（若用方向余弦方法时，要解一个方向余弦矩阵微分方程）即加速度计组件陀螺仪组件误差补偿姿态计算位置计算地球角速率计算姿态速率微分方程位移角速率微分方程位移角速率积分消除有害加速度及速度积分b iban iban bCb nC n epVn enωij Cb ibωb inωn ieωe ieω,,L λα,,ψθγ载体计算机图6-1-2 捷联式惯导系统原理+-++n b C 12b nb ω= qq•（1）姿态和航向角的计算图6-1-4 游动方位系统导航坐标系 与 系之间关系O abψab ψaz by ay ax bx θθγbz γθabψγn b 图6-1-3 游动方位系统平台航向角 与 、 之间的关系αψabψOy α()t y N by tx ab ψαψ载体的姿态可用航向角、俯仰角和横滚角表示。
假定开始时,载体坐标轴与导航坐标系完全重合。
进行图6-1-4所示的三次旋转可以到达的位置。
三次旋转方向余弦矩阵由下式得到b b b ox y z a a a ox y z b b b ox y zc o s c o s sin sin sin c o s sin sin sin c o s sin c o s c o s sin c o s c o s sin sin c o s c o s sin sin sin sin c o s sin c o s c o s c o s a b a b a b a b b n a b a b a b a b a b a b C γψγθψγψγθψγθθψθψθγψγθψγψγθψγθ+−+−⎡⎤⎢⎥=⎢⎥⎢⎥−−−⎣⎦记111213212223313233bnT T T CT T T T T T ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦值得注意的是横滚角和偏航角分别是定义在和之间,所以他们都存在多值问题,平台航向角的真值可根据表6-1的符号来确定，计算机程序框图如图6-1-5。
[1800]−，181231133312122s i n ()t a n ()t a n()a ba bT T T T T θγψψψα−−−==−=−=−γab ψ[0]，360ab ψ22T ε>12122tan ab T T ψ−=主Yes220T >ab ab ψψ=主abψ2ab ab ψψπ=+主NoYesab ab ψψπ=+主32abπψ=210T >2ab πψ=YesNoNoabψ210T >NoYesb n C 元素是时间的函数。
为求()b n C t 需要解方向余弦矩阵微分方程：b b b n n nbC C =Ω 式中，bnbΩ为角速度[,,]b b b b T nb nbxnby nbzωωωω=组成的反对称矩阵。
上式两边转置，则可得到方向余弦矩阵微分方程的另一种形式即b b b n nb nC C =−Ω 它们都对应九个一阶微分方程。
通过求解，可得()bn C t从第一章可知，四元数微分方程的表达式为,式中的是载体坐标系相对地理坐标系的旋转角速度的斜对称矩阵，其表达式为b =Ω q q bΩ1231232313122222X Y Z X Z Y Y X Z Z Y XP P P P P P P P P P P P λωωωλωωωλωωωλωωω••••=−−−=+−=+−=+−解微分方程，则令211d 20()()t b t tt et Ω∫=q q []000d 00x y z t x z y b t y z x z y x t θθθθθθθθθθθθθ−Δ−Δ−Δ⎡⎤⎢⎥ΔΔ−Δ⎢⎥Δ=Ω=⎢⎥Δ−ΔΔ⎢⎥ΔΔ−Δ⎢⎥⎣⎦∫传统的姿态更新算法有欧拉角法、方向余弦法和四元数法。
其中四元数法算法简单，计算量小，因而在工程实际中经常采用。
但在四元数法中不可避免地引入了不可交换误差，特别是在载体处在高动态环境时，这种误差就会很大，必须采取有效措施加以克服。
七、八十年代，JOHN E.BORTZ、MILLER等人对旋转矢量进行了研究，并指出了旋转矢量在捷联惯性导航中的应用，为设计高精度的捷联惯性导航系统提供了理论基础和思路下面我们分别从这几个方面来研究等效旋转矢量算法:a. 旋转矢量的概念b. 旋转矢量及其与四元数、方向余弦、欧拉角的关系c. 等效旋转矢量微分方程d. 姿态算法的比较设动坐标系在起始时刻t0与参考坐标系重合，记为000Z Y OX ,在时刻t 历经具体转动而到达t t t Z Y OX 位置。
由理论力学可知，不管具体转动如何，我们都可以等效的认为动坐标系在起始位置000Z Y OX 依次三个轴转动三次而到达t t t Z Y OX 的位置，并称对应三次转动的角度为一组欧拉角。
但事实上，我们也可以等效的认为通过绕某一瞬时轴转过一定的角度依次到达t 时刻位置t t t Z Y OX 。
如果记转过的角度为φ，沿瞬时轴方向的单位矢量为n那么我们便将矢量n φ=Φ称为等效描述刚体转动的旋转矢量，简称为旋转矢量。
(a)旋转矢量与四元数[][]bnr I r⎟⎟⎠⎞⎜⎜⎝⎛×Φ−+×Φ+=22cos 1sin φφφφ上式表明当我们知道描述两坐标系间的旋转矢量时，我们便可以进行矢量在两坐标系间的坐标变换，所以在导航系统中，我们能用旋转矢量来形成更新载体姿态矩阵的新算法，这种新算法比传统的四元数法或方向余弦法的精度高，计算量小，其性能十分优越。
（b ）旋转矢量与方向余弦矩阵若记将矢量在动坐标系上的坐标值变换到参考坐标系的姿态转换矩阵为n b C ，那么：bnbnrC r=由于r 为动坐标系上的任意矢量，所以比较可得：[][]⎟⎟⎠⎞⎜⎜⎝⎛×Φ−+×Φ+=22cos 1sin φφφφI C nb（a ）转动的不可交换性在力学中，刚体的有限转动是不可交换的。
如果刚体先绕X 轴转动90°，再绕Y 轴转动90 °，和先绕Y 轴转动90 °，再绕X 轴转动90 °，两种情况的结果显然是不同的。
这就是转动的不可交换性。
（b ）等效旋转矢量微分方程(Bortz 方程)利用上节给出的旋转矢量与四元素之间的关系可得2sin()12sin()[cos()2sin()]cos()2222222ωφφφφφφφφφωωφφφΦ⋅⎧=⎪⎪⎨⎪ΦΦ+−=Φ+⎪⎩2()()ωωωφΦΦ=ΦΦ⋅− ()/()/φωφωφωφΦ=ΦΦ⋅=ΦΦ+ 可得到等效旋转矢量微分方程，方程如下：)(])cos 1(2sin 1[1212ωφφφφωω×Φ×Φ−−+×Φ+=Φ 又因为⎥⎥⎦⎤⎢⎢⎣⎡−⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛−⎟⎠⎞⎜⎝⎛−==− 7532472512945224512312222)cos 1(2sin φφφφφφφφφφφctg−−−−=30240720121642φφφ代入等效旋转矢量微分方程可得:2411()()()21272030240φφωωωωωΦ=+Φ+ΦΦ+ΦΦ+ΦΦ+ 由于姿态更新周期一般都很短，φ角很小，φφ的高次项可略去不计，得到工程中常用的近似方程:11()212ωωωΦ=+Φ+ΦΦ 11()212ωωωΦ=+Φ+ΦΦ （c ）四元数更新方程设n 为导航坐标系，b 为机体坐标系，r 为某一向量。