捷联惯导系统_姿态算法(矩阵)
捷联惯导基本算法与误差
姿态计算 矩阵方程精确解1
二、方向余弦矩阵微分方程及其解 C C
E C E b C b b Eb
其中
b Eb
0 z y
z 0
x
y x
0
导航计算可以得到 E IE
b E E 有 b C C iE E iE b
E b E b
E C E b E C E （解 C b b ib iE b
的第一项）
增量算法 矩阵方程CS参数
sin 0 1 cos 0 b b 2 C (t t ) C (t ) I ib ( ib ) 2 0 0 展开合并上式，得 CbE (t t ) CbE (t )
姿态计算 姿态航向角计算1
四、姿态和航向角的计算 根据载体和地理坐标系之间的方向余弦矩阵可确定姿态、航向角
cos cos b CE cos sin sin sin cos cos sin cos sin sin sin cos sin sin sin cos cos sin sin cos cos sin sin cos sin cos cos
E b E b
n 1 n
b b b 02 ( EbX ) 2 ( EbY ) 2 ( EbZ )2
b Eb
方向不变时的精确解
九个微分方程求解，计算量大
姿态计算 四元数精确解1
三、四元数微分方程式及其解 由第一章，四元数微分方程式：
b q q
对
b 的处理类似上一节
一、角增量算法 角增量：陀螺仪数字脉冲输出，每个脉冲代表一个角增量 一个采样周期内，陀螺输出脉冲数对应的角增量为：
捷联惯性导航原理
2.捷联惯导力学编排方程
姿态角定义： ψ航向角----载体纵轴在水平面的投影与地理子午线之间 的夹角，用ψ表示，规定以地理北向为起点，偏东方向 为正，定义域0~360°。 θ俯仰角----载体纵轴与纵向水平轴之间的夹角，用θ表 示，规定以纵向水轴为起点，向上为正，向下为负，定 义域-90 ° ~+90 ° 。 γ横滚角----载体纵向对称面与纵向铅垂面之间的夹角， 用γ表示，规定从铅垂面算起，右倾为正，左倾为负， 定义域-180 ° ~+180° 。（载体纵向对称面和 纵轴空 间 铅垂面）
捷联惯性导航原理
2010.11.30 北航通信导航与自动测试实验室
如果载体真实地理位置以纬度、经度、高度 表示，则与此对应的载体在地球坐标系中的 真实位置(x，y，z)可通过下式求得:
地球各点重力加速度近似计算公式: g=g0(1-0.00265cos&)/1+(2h/R) g0:地球标准重力加速度9.80665(m/平方秒) &:测量点的地球纬度 h:测量点的海拔高度 R: 地球的平均半径(R=6370km) s:时间 ？？？？？？？？？？？？？？？？？？？？
f 为地球椭球模型的椭圆度，f= 1/298.257223563
R1 RN h R2 RM h
注意从瞬时速度过来那条线，用来计算w（enn）
3、捷联惯导系统的算法
3.1 姿态更新算法 四元数法：
Q(q0 , q1 , q2 , q3 ) q0 q1i q2 j q3k
1. 惯性导航中的常用坐标系
yt
yb
z e zi
北
xb
zb
zt
xt
O
东
Oe
捷联惯导系统解读
Q cos
u sin
2(q1q2 q0 q3 )
2 2 q0 q12 q22 q3
2(q2 q3 q0 q1 )
2(q1q3 q0 q2 ) 2(q2 q3 q0 q1 ) 2 2 q0 q12 q2 q32
T11 T21 T31 C bn T T T 12 22 32 T13 T23 T33
1 sin (T32 ) T31 1 tan ( ) 主 T 33 1 T 主 tan ( 12 ) T22
b nb x b 0 nby b 1 cos tan nb z 0
cos cos sin
当 90 时，方程退化，故不能全姿态工作。
捷联惯导系统
2.2 方向余弦法（九参数法）
n C n ωbk C b b nb
0 [ G ] Gz Gy
Gz
0 Gx
Gy Gx 0
K x [ K ] 0 0
0
Ky
0
0 0 Kz
捷联惯导系统
捷联惯导系统误差方程
b b b n n ωnb ωib Cn Cnωin
矢量的方向余弦表示姿态矩阵的方法； 可全姿态工作，但需要解含有九个未知量的线性方程组，计算量大， 工程上不实用。
捷联惯导系统
2.3 四元数法（四参数法）
2.3.1 四元数基本概念 四元数是由一个实数单位1和一个虚数单位i、j、k组成的含有四个 元的数。（超复数） Q q0 , q1, q2 , q3 q0 q1i q2 j q3k 四元数的大小——范数
捷联惯导算法与组合导航原理讲义
捷联惯导算法与组合导航原理讲义一、捷联惯导算法捷联惯导（Inertial Navigation System，INS）是一种通过测量惯性传感器的运动参数实现导航定位的技术。
惯性导航系统中包括了加速度计和陀螺仪等传感器，通过测量物体的加速度和角速度，可以推算出物体的位置、速度和姿态等信息。
1.1加速度计加速度计是一种测量物体加速度的传感器。
常见的加速度计有基于压电效应的传感器和基于微机电系统（Microelectromechanical System，MEMS）的传感器。
加速度计的原理是通过测量物体受到的惯性力，推算出物体的加速度。
由于加速度是速度对时间的导数，因此通过对加速度的积分操作，可以计算出物体的速度和位移。
1.2陀螺仪陀螺仪是一种测量物体角速度的传感器。
常见的陀螺仪有机械陀螺仪和MEMS陀螺仪等。
陀螺仪的原理是基于角动量守恒定律，通过测量转动惯量的变化，推算出物体的角速度。
与加速度计类似，通过对角速度的积分操作，可以计算物体的姿态。
1.3捷联惯导算法离散时间模型中，位置、速度和姿态等状态变量通过积分加速度和角速度来更新。
由于加速度计和陀螺仪测量结果存在噪声，因此在积分操作时需要加入误差补偿算法来消除误差。
常见的误差补偿算法有零偏校正和比例积分修正等。
连续时间模型中，位置、速度和姿态等状态变量通过微分方程来描述，并通过求解微分方程来更新状态。
由于计算量较大，通常需要使用数值积分方法来求解微分方程。
常见的数值积分方法有欧拉法、中点法和四阶龙格-库塔法等。
二、组合导航原理组合导航是一种融合多种导航技术的导航方式。
常见的组合导航方式有捷联惯导与GPS组合导航。
组合导航通过融合多种导航系统的测量结果，可以提高导航定位的精度和可靠性。
2.1捷联惯导与GPS组合导航捷联惯导与GPS组合导航是一种常见的组合导航方式。
在这种方式下，捷联惯导提供了高频率的惯导数据，可以提供较高的定位精度，但是由于其测量结果累积误差较大，会逐渐偏离真实轨迹。
车载捷联惯导系统基本原理
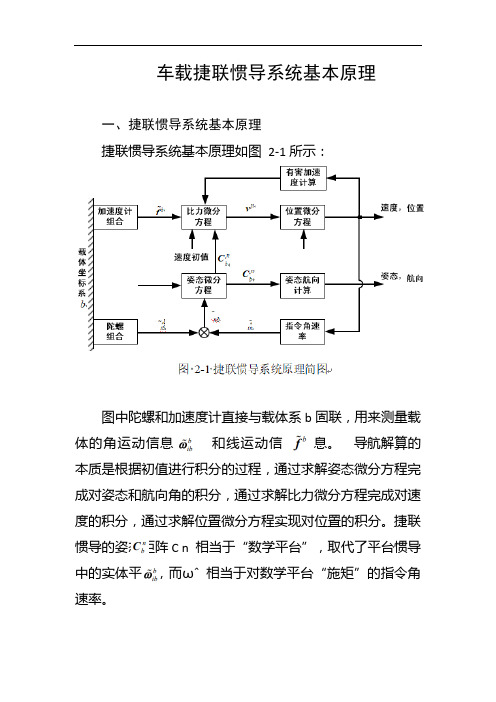
车载捷联惯导系统基本原理一、捷联惯导系统基本原理捷联惯导系统基本原理如图2-1所示：图中陀螺和加速度计直接与载体系b固联，用来测量载体的角运动信息和线运动信息。
导航解算的本质是根据初值进行积分的过程，通过求解姿态微分方程完成对姿态和航向角的积分，通过求解比力微分方程完成对速度的积分，通过求解位置微分方程实现对位置的积分。
捷联惯导的姿态矩阵C n 相当于“数学平台”，取代了平台惯导中的实体平台，而ωˆ相当于对数学平台“施矩”的指令角速率。
二、捷联惯导微分方程（一）姿态微分方程在捷联惯导系统中，导航坐标系n 和载体坐标系b 之间的角位置关系通常用姿态矩阵、四元数和欧拉角表示，相应也存在姿态矩阵微分方程、四元数微分方程和欧拉角微分方程三种形式。
姿态矩阵微分方程的表达式为：在欧拉角微分方程式(2.2-7)中，当俯仰角θ趋于90º时，cosθ趋于0，tanθ趋于无穷，方程存在奇异性，所以这种方法不能在全姿态范围内正常工作；姿态矩阵微分方程式(2.2-1)可全姿态工作，但姿态矩阵更新相当于求解包含9个未知量的线性微分方程组，计算量大；四元数微分方程式(2.2-6)同样可以全姿态工作，且更新算法只需求解4个未知量的线性微分方程组，计算量小，算法简单，是较实用的工程算法。
（二）速度微分方程速度微分方程即比力方程，是惯性导航解算的基本关系式：三、捷联惯性导航算法捷联惯导解算的目的是根据惯性器件输出求解载体姿态、速度和位置等导航信息，实际上就是求解三个微分方程的过程，相应存在姿态更新算法、速度更新算法和位置更新算法。
（一）姿态更新算法求解微分方程式(2.2-6)可得四元数姿态更新算法为：在车辆行驶过程中，一般不存在高频大机动环境，并且车载导航系统往往不工作在纯惯性导航方式，而是利用里程仪或零速条件进行组合导航，所以算法误差的影响有限，常用的5ms采样周期和二子样优化算法即可满足要求。
四、捷联惯导误差模型传感器误差、初值误差和算法误差是SINS的主要误差源，其中器件误差和初值误差又是影响导航结果的主要因素。
捷联惯导结算原理
0 cos sin ， Rz sin 0 cos
sin cos 0
0 0 1
cos cos sin sin sin cos cos sin sin cos sin cos T11 T12 T13 Ry Rx Rz cos sin cos cos sin T21 T22 T23 sin cos cos sin sin sin sin cos sin cos cos cos T T T 31 32 33 b 由姿态矩阵 C n 反解飞行器姿态欧拉角：
（5） 速度的计算
t t t t t 0 2iez etz ety 2iey Vxt Vx 0 t t b t t t t 0 2iex etx Vyt 0 Vy Cb f 2iez etz t Vz g Vzt 2 t t 2 t t 0 iey ety iex etx
o o sin 1 T23 , 90 , 90
tg 1
T13 180o , 180o , T33
tg 1
T21 o o , 180 , 180 T 22
图 6 东向北向速度变化曲线
阶段总结：1.学习了平台式和捷联式惯导的惯导解算方法并进行了仿真计算。 2.平台式惯导物理平台时刻跟踪当地水平东北天地理系， 加速计的比 力信息直接投影在导航系中，可直接进行导航速度和位置解算。载体的姿态可直 接从平台框架直接得出；而捷联式惯导用数学平台取代实体的物理平台，通过求
基于四元数姿态估计的捷联惯导初始对准算法
第34卷第9期传感技术学报Vol.34No.9 2021年9月CHINESE JOURNAL OF SENSORS AND ACTUATORS Sept.2021Initial Alignment Algorithm for SINS Based onQuaternion Attitude EstimationZHOU Xiaoren,ZHAO Heming"(School of Electronic and Information Engineering,Soochow University,Suzhou Jiangsu215006,China)Abstract:The performance of the traditional in-motion OBA coarse alignment algorithm of the strapdown inertial navigation system is degraded by the biases of gyroscopes,especially in low-precision sensors whose accumulated errors reduce the accuracy of the observation vectors.To solve this problem,the quaternion-based Unscented Kalman filter is studied in this paper to estimate the attitude of the carrier.Then the gyroscope biases can be estimated and eliminated effectively in the prediction equation,which suppresses the accumulated errors and improve the convergence precision of the attitude error angle.Finally,the simulation and field tests are carried out to verify the effectiveness of the algorithm studied in this paper.Key words:strapdown inertial navigation system；coarse alignment;attitude estimation；quaternion；unscented Kalman filterEEACC：7230doi：10・3969/j・iss n・1004-1699・2021・09・007基于四元数姿态估计的捷联惯导初始对准算法周晓仁，赵鹤鸣*(苏州大学电子信息学院，江苏苏州215006)摘要：针对传统动基座捷联惯导系统OBA粗对准算法，在低精度传感器中，易受到陀螺零偏的影响,存在累计误差导致观测矢量精度低的缺点，本文研究了基于四元数的无迹卡尔曼滤波来进行载体的姿态估计。
基于四元数方法的姿态解算
基于四元数方法的姿态解算方法分析摘要:载体的姿态解算算法是实现捷联式惯性导航系统精确导航的核心技术之一。
分析了欧拉法、方向余弦法、四元数法求解姿态矩阵的优缺点，采用四元数法与方向余弦法两种解算方法分别计算载体姿态，两种方法的计算结果之差与理论真值比较以得到解算的相对误差，从而验证了四元数法的正确性和有效性。
最后，指出提高采样频率和采用高阶计算算法能进一步减小姿态解算误差。
数字化仿真与转台试验结果表明，本文提出的载体姿态解算法具有良好的实时性。
1引言捷联惯导是一种自主式的导航方法。
该方法将陀螺仪和加速度计直接安装在载体上，省掉机电式导航平台，利用计算机软件建立一个“数学平台”来代替机电平台实体[1]。
由于其结构简单且抗干扰能力强，目前已成为航空航天、航海、机器人、智能交通等领域的研究热点之一。
姿态解算是捷联式惯性导航系统的关键技术，通过姿态矩阵可以得到载体的姿态和导航参数计算需要的数据，是捷联式惯导算法中的重要工作。
载体的姿态和航向体现了载体坐标系与导航坐标系之间的方位关系，确定两个坐标系之间的方位关系需要借助矩阵法和力学中的刚体定点运动的位移定理。
通过矩阵法推导方向余弦表，而刚体定点运动的位移定理表明，定点运动刚体的任何有限位移都可以绕过定点的某一轴经过一次转动来实现。
目前描述动坐标相对参考坐标系方位关系的方法有多种，可简单地将其分为3类，即三参数法、四参数法和九参数法「1-2]。
三参数法也叫欧拉角法，四参数法通常指四元数法，九参数法称作方向余弦法。
欧拉角法由于不能用于全姿态飞行运载体上而难以广泛用于工程实践，且实时计算困难。
方向余弦法避免了欧拉法的“奇点”现象，但方程的计算量大，工作效率低。
随着飞行运载体导航控制系统的迅速发展和数字计算机在运动控制中的应用，控制系统要求导航计算环节能更加合理地描述载体的刚体空间运动，四元数法的研究得到了广泛重视。
本文全面分析了3种解算方法的特点，通过对比四参法与九参法的计算结果以验证四元数法的正确性和有效性，基于数值仿真和转台实验相结合的分析方法得到进一步减少姿态解算误差的有效途径，为捷联式惯性导航技术的工程实践提供参考。