矩阵分解在推荐系统中的应用1
矩阵分解在推荐系统的应用

矩阵分解在推荐系统的应用随着互联网的发展和电子商务的兴起,推荐系统逐渐成为用户获取信息和商品的重要途径。
推荐系统的核心目标是根据用户的历史行为和个人偏好,预测和推荐用户可能感兴趣的信息和商品。
为了实现准确的推荐,矩阵分解作为一种常用的方法被广泛应用在推荐系统中。
矩阵分解是一种数学方法,它将一个大的矩阵分解为两个较小的矩阵的乘积。
在推荐系统中,矩阵分解可以被用来对用户和商品之间的关系进行建模。
通过将用户-商品评分矩阵分解为用户特征矩阵和商品特征矩阵,推荐系统可以通过计算用户和商品之间的相似度来预测用户对未知商品的喜好程度。
首先,推荐系统需要收集用户的历史行为数据,例如用户购买记录、评分和点击行为等。
这些数据可以表示为一个稀疏的用户-商品评分矩阵,其中行表示用户,列表示商品,每个元素表示用户对商品的评分或行为。
然后,通过矩阵分解,可以将用户-商品评分矩阵分解为用户特征矩阵和商品特征矩阵。
用户特征矩阵是一个N×K的矩阵,其中N是用户的数量,K是特征的数量。
每一行表示一个用户,每一列表示一个特征。
特征可以是用户的年龄、性别、兴趣爱好等。
同样,商品特征矩阵是一个M×K的矩阵,其中M是商品的数量。
每一行表示一个商品。
通过计算用户特征矩阵和商品特征矩阵之间的相似度,推荐系统可以预测用户对未知商品的评分。
矩阵分解的优势在于它可以充分利用用户和商品之间的隐含关系。
通过分解用户-商品评分矩阵,推荐系统可以挖掘用户和商品的潜在特性,从而更好地理解用户的偏好和商品的特点。
此外,矩阵分解还可以减轻数据稀疏性问题,因为通过用户特征矩阵和商品特征矩阵的乘积,可以填充原始评分矩阵中的缺失值。
矩阵分解在推荐系统中的应用不仅限于常见的商品推荐,还可以扩展到其他领域。
例如,在电影推荐系统中,矩阵分解可以用来为用户推荐适合其口味的电影。
在社交网络中,矩阵分解可以用来预测用户之间的社交关系。
此外,矩阵分解还可以应用在音乐推荐、新闻推荐和广告推荐等多个领域。
Python中的矩阵分解应用技巧

Python中的矩阵分解应用技巧矩阵分解是一种对矩阵进行分析和降维的有效算法。
随着大数据和机器学习的发展,矩阵分解在许多领域得到了广泛应用,例如推荐系统、图像处理、自然语言处理和社交网络分析等。
Python是一种流行的编程语言,拥有丰富的科学计算库和矩阵操作工具。
在Python环境中,进行矩阵分解可以使用各种库,例如NumPy、SciPy、Scikit-learn和TensorFlow等。
本文将探讨Python中的矩阵分解应用技巧,包括矩阵分解的概念、常用方法和实例应用。
1.矩阵分解的概念矩阵分解是一种将一个矩阵分解为多个较小矩阵的方法。
它可以用于降低矩阵的维度、简化数据结构和提取特征等。
在机器学习中,矩阵分解是一种实现数据降维的算法,它从高维数据中提取关键特征,使得数据可以更加有效地表示和处理。
矩阵分解的目标是将一个矩阵A分解为两个矩阵U和V的乘积。
其中,U是m×r的矩阵,V是r×n的矩阵,r是矩阵分解的秩。
因此,矩阵A的秩为r,且有A=UV。
在矩阵分解中,常用的方法有SVD(奇异值分解)、PCA(主成分分析)和NMF(非负矩阵分解)等。
下面将介绍这三种常用的矩阵分解方法以及它们的Python实现。
2.基于SVD的矩阵分解SVD是一种基于矩阵特征值和特征向量的分解算法。
它将一个矩阵分解为三个矩阵的乘积,即A=UΣV^T,其中U和V是正交矩阵,Σ是对角矩阵。
SVD的重要性在于它能够识别和提取矩阵的主成分,从而对矩阵进行降维和特征提取。
在Python中,使用NumPy库可以轻松地进行SVD。
例如,考虑以下代码:```import numpy as npA = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])U, S, Vt = np.linalg.svd(A)```该代码将矩阵A进行SVD分解,并返回分解后的矩阵U、S和Vt。
其中,S是矩阵A的奇异值,即矩阵Σ的对角线元素。
推荐系统的常用算法原理和实现

推荐系统的常用算法原理和实现推荐系统是将用户的兴趣和需求与商品或服务进行匹配,帮助用户发现他们可能感兴趣的内容。
在实践中,推荐系统使用各种不同的算法来实现这一目标。
以下是一些常见的推荐系统算法原理和实现的介绍。
1. 协同过滤算法(Collaborative Filtering)协同过滤算法是推荐系统中最常见的算法之一、它基于用户和物品之间的关联性来进行推荐。
协同过滤算法可以分为两类:基于用户的协同过滤和基于物品的协同过滤。
基于用户的协同过滤是通过找到与目标用户兴趣相似的其他用户,然后将他们的喜好推荐给目标用户。
基于物品的协同过滤则是找到与目标物品相似的其他物品,并将这些相似物品推荐给目标用户。
2. 基于内容的推荐算法(Content-based Filtering)基于内容的推荐算法是根据用户对物品的历史行为和物品的特征信息来进行推荐。
该算法通过比较用户的兴趣和物品的特征来决定哪些物品是相似的,并推荐相似的物品给用户。
例如,如果一个用户喜欢电影A,基于内容的推荐算法可以找到其他电影,这些电影的类型,演员或导演与电影A相似,然后将这些相似的电影推荐给用户。
3. 矩阵分解算法(Matrix Factorization)矩阵分解算法是一种通过将用户-物品关联矩阵分解为两个低秩矩阵来进行推荐的算法。
通过低秩矩阵的分解,可以发现用户和物品之间的隐含特征,从而预测用户对未知物品的评分。
矩阵分解算法的一个典型应用是在电影推荐系统中,根据用户的评分数据,将用户和电影关联矩阵分解为用户-隐含特征矩阵和电影-隐含特征矩阵。
4. 多臂赌博机算法(Multi-Armed Bandit)多臂赌博机算法是一种用于在线推荐系统中的算法。
它基于动态调整推荐策略,根据用户的反馈来优化推荐结果。
多臂赌博机算法类似于一个赌博机,每个臂代表一种推荐策略,根据用户的反馈进行调整。
如果其中一种策略获得了较好的反馈,系统将更多地使用该策略进行推荐;如果其中一种策略获得了较差的反馈,系统将减少该策略的使用。
基于矩阵分解的情景感知个性化推荐法研究
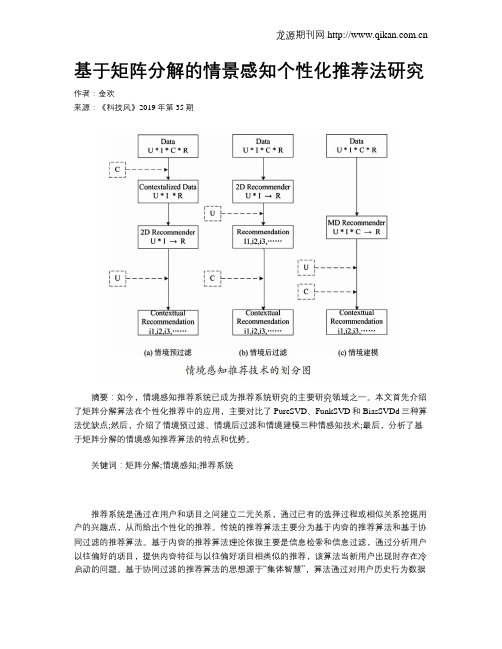
基于矩阵分解的情景感知个性化推荐法研究作者:金欢来源:《科技风》2019年第35期摘要:如今,情境感知推荐系统已成为推荐系统研究的主要研究领域之一。
本文首先介绍了矩阵分解算法在个性化推荐中的应用,主要对比了PureSVD、FunkSVD和BiasSVDd三种算法优缺点;然后,介绍了情境预过滤、情境后过滤和情境建模三种情感知技术;最后,分析了基于矩阵分解的情境感知推荐算法的特点和优势。
关键词:矩阵分解;情境感知;推荐系统推荐系统是通过在用户和项目之间建立二元关系,通过已有的选择过程或相似关系挖掘用户的兴趣点,从而给出个性化的推荐。
传统的推荐算法主要分为基于内容的推荐算法和基于协同过滤的推荐算法。
基于内容的推荐算法理论依据主要是信息检索和信息过滤,通过分析用户以往偏好的项目,提供内容特征与以往偏好项目相类似的推荐,该算法当新用户出现时存在冷启动的问题。
基于协同过滤的推荐算法的思想源于“集体智慧”,算法通过对用户历史行为数据的挖掘发现用户的偏好,基于不同的偏好对用户进行群组划分并推荐品味相似的商品。
协同过滤算法同样也存在冷启动的问题,当没新用户数据时,无法给出较好的推荐。
没有考虑情境的差异,比如不同根据季节的不同,给用户推荐与季节相适应的服饰。
基于以上问题,研究人员提出了基于矩阵分解的情境感知推荐法。
1 矩阵分解算法在个性化推荐中的应用矩阵分解的核心思想是将用户评分矩阵分解为低秩的矩阵,使其乘积尽可能接近原始评分矩阵,使得预测的矩阵与原始矩阵之间的误差平方最小。
奇异值分解(Singular Value Decomposition,以下简称SVD)在机器学习领域得到了广泛的应用,因为它不仅可以用于降维算法中的特征分解,还能用于推荐算法。
如果将m个用户和n个项目对应的评分看做一个矩阵M,本文将用矩阵分解来解决该问题。
1.1 PureSVD算法PureSVD(传统的奇异值分解)在降维中的应用,将用户和项目对应的m×n矩阵M进行SVD分解,通过选择部分较大的奇异值进行降维分解为:Mm×n=Um×k∑k×kVTk×n(1)其中k是矩阵M中的奇异值的个数,一般会小于用户数和项目数。
奇异值矩阵分解算法在推荐系统的应用效果

奇异值矩阵分解算法在推荐系统的应用效果推荐系统已经在我们的日常生活中扮演了越来越重要的角色。
无论是在电子商务平台上购物,还是在视频流媒体平台上观看影片,推荐系统都能够根据我们的兴趣和偏好,向我们推荐最相关的商品或内容。
为了实现更精准和个性化的推荐,奇异值矩阵分解(Singular Value Decomposition,简称SVD)算法被广泛应用于推荐系统中。
本文将探讨奇异值矩阵分解算法在推荐系统中的应用效果。
一、奇异值矩阵分解算法简介奇异值矩阵分解算法属于一种基于矩阵分解的协同过滤算法,通过将用户-物品评分矩阵分解为三个矩阵的乘积,对用户和物品的潜在特征进行建模。
这三个矩阵分别代表用户特征、物品特征和特征空间的权重。
在推荐过程中,通过计算用户和物品在特征空间上的相似度,给用户推荐与其兴趣最匹配的物品。
二、奇异值矩阵分解算法的原理在奇异值矩阵分解算法中,首先需要构建用户-物品评分矩阵。
该矩阵的行表示用户,列表示物品,每个元素表示用户对物品的评分。
然后,通过对评分矩阵进行矩阵分解,得到用户特征矩阵、物品特征矩阵和特征空间权重矩阵。
在计算用户特征矩阵和物品特征矩阵时,可以使用一种常见的优化算法——随机梯度下降。
该算法通过不断迭代更新模型参数,将预测评分与真实评分之间的误差最小化。
通过迭代优化算法,得到最佳的用户特征矩阵和物品特征矩阵。
最后,根据用户特征矩阵、物品特征矩阵和特征空间权重矩阵,可以计算用户和物品之间的相似度。
通过计算相似度,可以为用户推荐与其兴趣相符的物品。
三、奇异值矩阵分解算法的应用效果奇异值矩阵分解算法在推荐系统中的应用效果已经得到了广泛的验证和证明。
与传统的协同过滤算法相比,奇异值矩阵分解算法具有以下优势:1. 精准度高:奇异值矩阵分解算法能够对用户和物品进行更准确的建模,通过捕捉用户和物品的潜在特征,实现更个性化的推荐。
2. 冷启动问题:传统的协同过滤算法在面对新用户或新物品时存在冷启动问题,即无法准确预测新用户对新物品的兴趣。
矩阵奇异值分解的实际应用

矩阵奇异值分解的实际应用
矩阵奇异值分解(SVD)在实际中有很多应用,下面是其中的一些例子:
- 图像压缩:SVD可以将图像的大小最小化到可接受的质量水平,从而在相同磁盘空间中存储更多图像。
它利用了在SVD之后仅获得的一些奇异值很大的原理,通过修剪三个矩阵中的前几个奇异值,可以获得原始图像的压缩近似值,人眼无法区分一些压缩图像。
- 数据降维:在大多数应用中,我们希望将高秩矩阵缩减为低秩矩阵,同时保留重要信息。
SVD可以实现这一目标,通过保留前r个较大的奇异值,来近似表示原始矩阵,从而达到降维的目的。
- 推荐系统:在推荐系统中,SVD可以用于计算用户和项目之间的相似度。
通过将用户和项目的矩阵进行奇异值分解,可以得到一个包含奇异值和左右奇异向量的矩阵。
这些奇异值和奇异向量可以用于计算用户和项目之间的相似度,从而为用户推荐类似的项目。
总之,矩阵奇异值分解在数据压缩、数据降维、推荐系统等方面都有重要的应用,它可以帮助我们从高维数据中提取关键信息,同时保持数据的重要特征。
线性代数在人工智能中的应用

线性代数在人工智能中的应用人工智能(Artificial Intelligence,AI)是近年来发展迅猛的领域,它涵盖了机器学习、深度学习、自然语言处理等多个子领域。
而线性代数作为数学的重要分支,正发挥着不可或缺的作用。
本文将探讨线性代数在人工智能中的应用。
一、矩阵与向量在神经网络中的应用神经网络是人工智能领域中最为重要的技术之一。
在神经网络中,矩阵和向量的应用尤为广泛。
神经网络的训练过程可以看作是通过调整矩阵中的权重和偏置项,使得网络能够更好地拟合输入与输出之间的关系。
矩阵乘法在神经网络中被广泛使用,它将输入与权重相乘并加上偏置项,得到每个神经元的激活值。
而向量则可以表示神经网络中的输入、输出和中间结果,方便进行计算和推理。
二、特征值分解在降维中的应用在处理大规模数据时,降维是一个重要的问题。
特征值分解(Eigenvalue Decomposition)是线性代数中的一种方法,可以将一个矩阵分解为特征值和特征向量的乘积。
在降维中,我们可以通过特征值分解将高维数据映射到低维空间,从而减少数据的维度。
这样一来,不仅可以节省计算资源,还可以提高模型的训练速度和效果。
三、矩阵求逆在最小二乘法中的应用最小二乘法是一种常用的回归分析方法,它可以通过最小化误差的平方和来拟合数据。
在最小二乘法中,需要求解一个线性方程组,而矩阵求逆是解决线性方程组的一种常见方法。
通过求逆,可以得到方程组的解析解,从而得到最佳的拟合曲线。
然而,在实际应用中,矩阵求逆可能会面临数值稳定性的问题,因此需要采用其他方法,如QR分解或奇异值分解。
四、奇异值分解在图像处理中的应用奇异值分解(Singular Value Decomposition,SVD)是线性代数中的一种重要方法,可以将一个矩阵分解为三个矩阵的乘积。
在图像处理中,奇异值分解可以用于图像压缩和图像增强。
通过保留较大的奇异值,可以实现图像的压缩,减少存储空间的占用。
而通过过滤掉较小的奇异值,可以去除图像中的噪声和干扰,提高图像的质量。
矩阵分解的方法和应用

矩阵分解的方法和应用在机器学习和数据分析领域,矩阵分解是一个常用的技术手段。
通过对数据矩阵进行分解,我们可以得到数据的潜在特征和规律,从而更好地理解和利用数据。
本文将介绍矩阵分解的常见方法和应用。
一、基本概念矩阵分解是指将一个矩阵表示为若干个小矩阵(或向量)的乘积的形式。
这些小矩阵一般是具有特定结构或意义的,例如对称矩阵、正定矩阵、特征矩阵等等。
矩阵分解可以应用到各种场景,例如数据降维、矩阵压缩、矩阵重构、协同过滤等等。
二、矩阵分解的方法常见的矩阵分解方法有以下几种:1. 奇异值分解(SVD)奇异值分解是一种基础的矩阵分解方法。
它将一个矩阵分解为三个小矩阵的乘积形式:$A=U\Sigma V^T$,其中$U$和$V$是正交矩阵,$\Sigma$是奇异值矩阵。
通过特征值分解可以得到奇异值矩阵,从而实现矩阵分解。
奇异值分解可以用来进行数据降维和矩阵重构。
例如,我们可以将一个高维度的数据矩阵分解为低维度的奇异向量,从而实现数据降维;或者我们可以使用奇异向量重构原始的矩阵,从而实现数据压缩。
2. QR分解QR分解是一种将矩阵分解为正交矩阵和上三角矩阵的方法。
具体来说,对于一个矩阵$A$,可以分解为$A=QR$,其中$Q$是正交矩阵,$R$是上三角矩阵。
QR分解可以应用到求解线性方程组、估计模型参数等领域。
3. 特征值分解(EVD)特征值分解是指将一个方阵分解为正交矩阵和对角矩阵的乘积形式。
具体来说,对于一个方阵$A$,可以分解为$A=V\LambdaV^{-1}$,其中$V$是正交矩阵,$\Lambda$是对角矩阵,对角线上的元素就是矩阵$A$的特征值。
特征值分解可以用于矩阵压缩和数据降维。
三、矩阵分解的应用1. 推荐系统推荐系统是一种常见的应用场景,它可以根据用户历史行为和兴趣,向用户推荐可能感兴趣的物品。
矩阵分解可以应用到推荐系统中,其基本思路是利用用户对物品的评分矩阵,对其进行分解,得到用户和物品的特征向量,然后通过计算余弦距离等方法,计算出用户和物品之间的相似度,从而推荐给用户可能感兴趣的物品。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用矩阵分解预测缺失值的推荐算法
推荐系统的目标就是预测出符号“?”对应位置的 分值。推荐系统基于这样一个假设:用户对项目的 打分越高,表明用户越喜欢。因此,预测出用户对 未评分项目的评分后,根据分值大小排序,把分值 高的项目推荐给用户。
利用矩阵分解预测缺失值的推荐算法
矩阵分解目标就是把用户-项目评分矩阵R分解成用 户因子矩阵和项目因子矩阵乘的形式,即R=UV,这 里R是n×m, n =6, m =7,U是n×k,V是k×m。直 观地表示如下:
用数学表达的话,设用户向量是Nu,投影到U空间后的向量 为P,则有:
然后就可以计算这个用户(用P向量)与其他用户(Uk的各 行向量)之间的相似度了。大量的实验表明,计算相似度的 话还是使用欧式距离比较有效。上面的算法瓶颈是如何在 “茫茫人海”中找到最相似的那个User。
基于奇异值分解的推荐算法
使用基于物品的推荐不存在上面的计算瓶颈,因为我们探索 的是物品之间的相似度而不是用户之间的相似度。在大多数 系统中,物品比用户更稳定,不经常变化。所以,基于物品 的相似度非常适合预计算。 相类似的,如果要计算两Item之间的相似度需要使用Vk矩阵。 Vk 每一行代表一个Item,行之间越相近则代表Item之间越相 似。其计算过程与上面所讲的User之间的推荐过程很接近。
假定用S 乘以������ ,则有:
特征值与特征向量的意义
上例表明,即使������是一个任意的向量,用S 去乘以它 的效果都取决于S 的特征值及特征向量。另外,从 S ������ = 60 ������1 +80 ������2 +6 ������3,看出一个非常直观的结论就是, 相对而言,S ������的大小更不受S 的小特征值影响。上 例中,由于λ3=1,所以上式中最右边的加数的影响 较小。实际上,如果完全忽略上式的最右边对应于 λ3=1 的特征向量那么S������的结果就是(60,80,0)T而不是 正确结果(60,80,6)T,但是不论采用哪一种指标(比 如差向量的长度)来计算,这两个向量都相对比较 接近。这也意味着,对于矩阵-向量的乘积来说,较 小的特征值及其特征向量的影响也较小。
基于奇异值分解的推荐算法
【问】评分矩阵A,已知User=x, Item=y, 请问Rating=?
1) 从原始矩阵A中找到被User=x评过分的那些items;
2) 使用降维矩阵,找出被User=x评过分的跟Item=y最相似的那个Item;
3) 从原始矩阵A中获取被User=x评过分的最相似的Item的评分,并把这个 评分当做User=x对Item=y的评分。 与基于用户相似度推荐类似,在第二步计算中,如果Item=y已经在降维 矩阵中,则可计算;如果Item=y是一个新物品,则要先做投影,然后再 计算。
奇异值分解
特征值分解是一个提取矩阵特征很不错的方法,但 是它只是对方阵而言的,在现实的世界中,我们看 到的大部分矩阵都不是方阵,比如说有N个学生, 每个学生有M科成绩,这样形成的一个N * M的矩阵 就不可能是方阵,我们怎样才能描述这样普通的矩 阵呢的重要特征呢?奇异值分解可以用来干这个事 情,奇异值分解(SVD)是一个能适用于任意的矩阵的 一种分解的方法。
利用矩阵分解预测缺失值的推荐算法
高维的用户-项目评分矩阵分解 成为两个低维的用户因子矩阵 和项目因子矩阵,因此矩阵分 解和PCA不同,不是为了降维。 用户i对项目j的评分rij = <ui,vj>。 下面介绍评估低维矩阵乘积拟 合评分矩阵的方法。
首先假设,用户对项目的真实 评分和预测评分之间的差服从 高斯分布,基于这一假设,可 推导出目标函数如右图:
特征值与特征向量的意义
在数学上,特别是线性代数中,对于一个给定的线性变 换,它的特征向量V经过这个线性变换后,得到的新向 量仍然与原来的V保持在同一条直线上,但其长度也 许会改变.一个特征向量的长度在该线性变换下缩放 的比例称为其特征值. 对于特征向量,线性变换仅仅改变它们的长度,而 不改变它们的方向(除了反转以外),而对于其它 向量,长度和方向都可能被矩阵所改变。如果特征 值的模大于1,特征向量的长度将被拉伸,而如果特 征值的模小于1,特征向量的长度就将被压缩。如果 特征值小于0,特征向量将会被翻转。
矩阵分解在推荐系统中的应用(1)
重庆大学 余俊良
摘 要
• 线性代数基础知识
• 奇异值分解 • 梯度下降算法
• 一般矩阵分解 • 非负矩阵分解
• 上下文感知的矩阵分解 • 融合社会化信息的矩阵分解 • 实验分析
特征值与特征向量
对于M×M的方阵C 及非零向量������ ,有C ������ = λ ������ 。
设新的Item评分向量是Ni(mx1),处于U空间(m维),需要投影到Vk 空间(n维)。首先通过内积计算Ni在U空间中的坐标,然后使用Sk反向 伸缩坐标即可得到在V空间的坐标。
用数学表达的话,设用户向量是Ni,投影到V空间后的向量为P,则有:
基于奇异值分解的推荐算法
基于奇异值分解的推荐算法
SVD的缺点:
特征值与特征向量的意义
由上例可知,如果我们想要描述好一个变换,那我 们就描述好这个变换主要的变化方向就好了。看看 之前特征值分解的式子,分解得到的Σ矩阵是一个对 角阵,里面的特征值是由大到小排列的,这些特征 值所对应的特征向量就是描述这个矩阵变化方向 (从主要的变化到次要的变化排列)。
我们通过特征值分解得到的前N个特征向量,那么 就对应了这个矩阵最主要的N个变化方向。我们利 用这前N个变化方向,就可以近似这个矩阵(变 换)。也就是之前说的:提取这个矩阵最重要的特 征。
在第二步中,如果User=x已经在降维矩阵中,则按 上面步骤计算;如果User=x是一个新的用户,在计 算相似度之前,这个新用户必须冲n维空间投影到k 维空间中。
基于奇异值分解的推荐算法
如果知道SVD的空间几何意义,理解投影过程就很简单:原 来的用户的评分向量Nu(1xn)是在V空间中(n维),将其与Vk 矩阵相乘就知道这个用户向量的坐标,然后根据S进行坐标 缩放(同时截取前k个值即可),获得的坐标就是用户的评 分向量Nu在U空间中的坐标了。
基于奇异值分解的推荐算法
基于用户相似度的SVD推荐算法
【问】评分矩阵A,已知User=x, Item=y, 请问Rating=? 1) 从原始矩阵A中找出对Item=y评过分的所有用户;
2) 使用降维矩阵,找出对Item=y评过分的与User=x 最相近的那个User;
3) 从原始矩阵中获取最相似用户对Item=y的评分, 并把这个评分当做User=x对Item=y的评分。
奇异值分解
SVD能提供原始矩阵的最好的低阶线性近似。通过选取最大 的k个奇异值可以降低原始矩阵的维度。k的值会根据数据的 大小和结构而变化,一个典型的做法是保留矩阵中90%的能 量信息,即将奇异值的平方和累加到总值的90为止。在很多 情况下,前10%甚至1%的奇异值的和就占了全部的奇异值 之和的99%以上了。也就是说,我们也可以用前K个奇异值 来近似描述矩阵。
奇异值分解
令r 是M×N 矩阵C 的秩,那么C 存在如下形式的SVD:
U 是一个M×M 的矩阵,其每一列是矩阵CCT的正交 特征向量,而N×N 矩阵V 的每一列都是矩阵CTC 的 正交特征向量。 1.CCT 的特征值 λ1, λ2,…, λr 等于CTC 的特征值;
2.对于1≤ i ≤ r,令σi = λi ,并且 λi ≥ λi+1。M × N的 矩阵Σ 满足Σ ii=σi,其中1≤ i≤ r,而Σ 中其他元素均为 0。
设 V 和 W 是在相同域 K 上的向量空间。函数 f : V → W 被称为 是线性映射,如果对于 V 中任何两个向量 x 和 y 与 K 中任何标 量 a,满足下列两个条件: 可加性: ������ ������ + ������ = ������ ������ + ������(������)
简单来说就是,线性映射可以用矩阵-向量乘法表示。 在线性映射中,可以把N维向量投影到M维向量,N可以 不等于M.
当N==M时,也就是定义中的自同态映射.
特征向量与特征值在自同态的情况下产生.即N维到N 维的映射.
线性映射与矩阵
看下面几个二维空间自同态映射的例子.
逆时针旋转90 度 逆时针旋转θ 度:
SVD often raises difficulties due to the high portion of missing values caused by sparseness in the user-item ratings matrix. Conventional SVD is undefined when knowledge about the matrix is incomplete. Moreover, carelessly addressing only the relatively few known entries is highly prone to overfitting.
齐次性:
������ ������������ = ������������ ������
这等价于要求对于任何向量 x1, ..., xm 和标量 a1,..., am,方程 成立。
线性映射与矩阵
如果 V 和 W 是有限维的,并且在这些空间中有选择好 的基,则从 V 到 W 的所有线性映射可以被表示为矩阵; 如果 A 是实数的m×n矩阵,则规定f(x)=Ax描述一个线 性映射 Rn → Rm。
针对x轴反射
在所有方向上放大2 倍
挤压
向y轴投影
线性映射与矩阵
一个矩阵就是一个线性映射的描述,因为一个矩阵 乘以一个向量后得到的向量,其实就相当于将这个 向量进行了线性变换。
线性映射与矩阵
从前面的例子可以看到,矩阵对应了一个变换,是把 任意一个向量变成另一个方向或长度不同的新向量。 在这个变换的过程中,原向量主要发生旋转、伸缩的 变化。如果矩阵对某一个向量或某些向量只发生伸缩 变换,不对这些向量产生旋转的效果,那么这些向量 就称为这个矩阵的特征向量,伸缩的比例就是特征值。
