按叠加原理作弯矩图
梁的剪力和弯矩剪力图和弯矩图

2、计算1-1 截面旳内力 FA
3、计算2-2 截面旳内力
M2
F=8kN
FS1
M1 FS1 FA F 7kN M1 FA 2 F (2 1.5) 26kN m
q=12kN/m
FS2
FB
FS2 q 1.5 FB 11kN
M2
FB
1.5 q 1.5 1.5 2
30kN m
2
1
例题
求下图所示简支梁1-1与2-2截面旳剪力和弯矩。
F=8kN
q=12kN/m
A 2m
FA 1.5m
1 1 1.5m
2
B
2
1.5m
3m
FB
解: 1、求支反力
3 M B 0 FA 6 F 4.5 q 3 2 0 FA 15kN
Fy 0 FA FB F q 3 0 FB 29kN
梁任意横截面上旳剪力,等于作用在该截面左边 (或右边)梁上全部横向外力旳代数和。截面左 边向上旳外力(右边向下旳外力)使截面产生正旳 剪力,反之相反。【左上右下为正,反之为负】 梁任意横截面上旳弯矩,等于作用在该截面左 边(或右边)全部外力(涉及外力偶)对该截面 形心之矩旳代数和。截面左边(或右边)向上旳 外力使截面产生正弯矩,反之相反。【左顺右逆 为正,反之为负】
一、梁平面弯曲旳概念
1、平面弯曲旳概念
弯曲变形:作用于杆件上旳外力垂直于杆件旳轴线,使 杆旳轴线由直线变为曲线。
平面弯曲:梁旳外载荷都作用在纵向对称面内时,则梁旳轴 线在纵向对称面内弯曲成一条平面曲线。
q F
Me 纵 向
对称面
B
A
x
y FAy
FBy
以弯曲变形为主旳直杆称为直梁,简称梁。 平面弯曲是弯曲变形旳一种特殊形式。
建筑力学中应用叠加法绘制弯矩图的新探讨
建筑力学中应用叠加法绘制弯矩图的新探讨作者:程晶晶来源:《科技资讯》2023年第16期关键词:建筑力学叠加法矩图探讨中图分类号: G64 文献标识码: A 文章编号: 1672-3791(2023)16-0150-04力学的概念起源于古人对自然现象的观察、在自然界生产活动过程中总结的经验。
16—17 世纪,力学开始发展成为一门相对独立、系统的自然科学门类。
建筑力学是建筑行业的基础课程,它旨在帮助学生们更好地理解建筑结构的客观特征,并掌握结构构件的受力特性,从而为建筑设计和施工提供坚实的基础。
通过应用叠加原理,我们可以使用一种全面的、多维度的分析和综合方法。
通过叠加原理,当结构构件处于弹性范围内,受到多种荷载的共同影响,其反应将会以线性方式发展,也就是说,每种荷载的影响都会相当于它们单独施加的力的总和。
在分析问题和解决问题上,是把复杂的研究问题,分解为若干个简单问题,在分析的基础上分别解决各个简单问题,然后将各个简单问题统一到复杂的研究问题上来,使复杂问题得到解决。
叠加法是一种将建筑物的力学和结构紧密联系起来的方法。
1 相关概念概述弯矩图描绘了杆件在不同截面上的弯曲变形情况。
曲线可以被广泛理解,从简单的直线到复杂的曲线,甚至可以被称为普遍的曲线。
弯矩图可以用来描述结构物的弯曲力,它们通常出现在受力部位,不需要标注正负值。
1.1 弯矩图的特征绘制弯矩图时,有两个关键步骤:首先,要准确描绘出曲线的形状,即确定弯矩图的特征;其次,要确定曲线的位置,即在已知曲线的形状和大小的基础上,确定平面曲线的位置,这就要求先确定曲线上任意两点的位置,这两点的位置就是指某两个截面处的弯矩值[1]。
可见,弯矩曲线的绘制过程主要是进行如下两个步骤:(1)确定图形特征和特征值;(2)可以得出某两个截面上的弯矩值。
1.2 绘制方式首先,根据单跨梁的特性和规律,绘制出附属部分的弯矩图,然后再将其延伸至基本部分,以获得更准确的结果。
单跨超静定梁的杆端弯矩和杆端剪力

Δ1=δ11X1+δ12X2+δ13X3+Δ1P=0
Δ2=δ21X1+δ22X2+δ23X3+Δ2P=0
b
Δ3=δ31X1+δ32X2+δ33X3+Δ3P=0
式(b)就是由位移条件所建立的求解X1、X2和X3
对于n次超静定结构有n个多余约束,也就是有n 个多余未知力x1,x2,…,xn,且在n个多余约束处 有n个已知的位移条件,故可建立n个方程,例如原 结构在荷载作用下各多余约束处的位移为零时,有
11E 1 I
M 1 2dx1(1ll2l)l3 E I2 3 3E I
1
11q l2 3 q l4
1 P E IM 1 M P d x E I(3 2l l 4 l) 8 E I
区段叠加法作弯矩图

1、掌握叠加原理; 2、会用叠加法作弯矩图; 3、会用区段叠加法作弯矩图
重 点
1、叠加法绘制弯矩图 2、区段叠加法绘制弯矩图。
难 点
区段叠加法绘制弯矩图
叠加原理: 几个载荷共同作用的效果,等于各个载荷单独作用效果之和 “效果”——指载荷引起的反力、内力、应力或变形 “之和”——代数和 叠加原理成立的前提条件:小变形条件
+
1 Fl 8
+
1 Fl 4
6kN 6kN
A
2kN m
B
2kN m
D
C
2m
2m
4
2m
2m
2m
2m
+
+
4
6
4
-
MA A
q
MB B
l A
q
B A
MA
MB B
l
l
+
MA 1/8qL2
+
MB 1/8qL2 MA
+
MB
区段叠加法——用叠加法作某一段梁弯矩图的方法 原理
任意段梁都可以当作简支梁,并可以利用叠加法来作该段梁 的弯矩图
M x M1 x M 2 x
qx2 M x Fx 2
q
B
A F
X
l
叠加法——用叠加原理绘制弯矩图的方法
叠加时,易先画直线形的弯矩图,再叠加曲线形或折线形 的弯矩图 由于剪力图比较好画,重点介绍用叠加法画弯矩图
步骤:
1. 荷载分解 2. 作分解荷载的弯矩图
3. 叠加作荷载共同作用下 的弯矩图
注意:
弯矩图的叠加, 不是两个图形的简单叠加, 而是对应点处纵坐标的相加。
结构力学 叠加法

2.6叠加法作弯矩图当梁在荷载作用下变形微小,因而在求梁的支反力、剪力、弯矩时可直接代入梁的原始尺寸进行计算,且所得结果与梁上荷载成正比。
在这种情况下,当梁上有几项荷载作用时,由每一项荷载所引起的梁的支反力或内力,将不受其他荷载的影响。
所以在计算梁的某截面上的弯矩时,只需先分别算出各项荷载单独作用时在该截面上引起的弯矩,然后求它们的代数和即得到该截面上的总弯矩。
这种由几个外力共同作用引起的某一参数(内力、位移等)等于每一外力单独作用时引起的该参数值的代数和的方法,称为叠加法。
叠加法的应用很广,它的应用条件是:需要计算的物理量(如支反力、内力以及以后要讨论的应力和变形等)必须是荷载的线性齐次式。
也就是说,该物理量的荷载表达式中既不包含荷载的一次方以上的项,也不包含荷载的零次项。
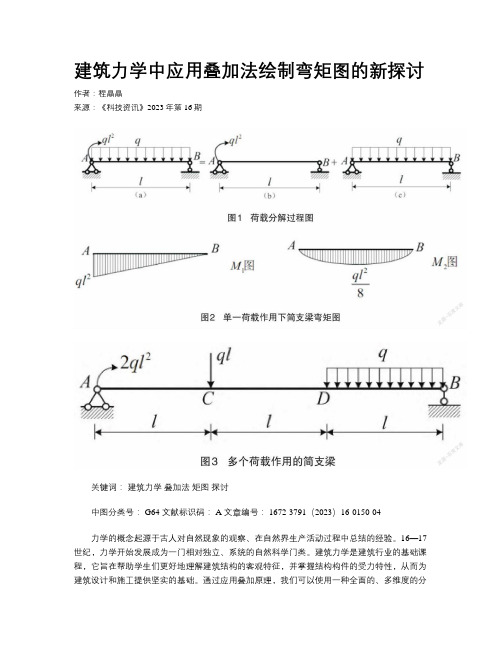
例题2-9试按叠加原理做例题2-9图(a)所示简支梁的弯矩图。
求梁的极值弯矩和最大弯矩。
解:先将梁上每一项荷载分开(见图(b)、图(c)),分别做出力偶和均布荷载单独作用的弯矩图(见图(d)、图(e))两图的纵坐标具有不同的正负号,在叠加时可把它们画在x 轴同一侧(见图f)。
于是两图共有部分,其正、负纵坐标值互相抵消。
剩下的纵距(见图(f)中阴影线部分)即代表叠加后的弯矩值。
叠加后的弯矩图仍为抛物线。
如将它改画为以水平直线为基线的图,即得通常形式的弯矩图(见图(曲)。
求极值弯矩时,先要确定剪力为零的截面位置。
由平衡方程0Bm =∑可求得支反,剪力方程为Q 即可求出极值弯矩所在截面的位置。
令()0x极值弯矩为由例题2-9图(g)可见,全梁最大弯矩为本例中的极值弯矩并不大于梁的最大值弯矩。
当梁上的荷载较复杂时,也可将梁按荷载情况分段,求出每一段梁两端截面的内力。
这时该段梁的受载情况等效于一受相同荷载的简支梁 (见图2-12(a)、(b))。
因为每一段梁在平面弯曲时的内力,不外是轴力N、剪力Q和弯矩M。
由于轴力N不产生弯矩,故在作弯矩图时可将它略去,剩下的梁端剪力1Q,2Q和梁端弯矩1M、2M,及荷载对梁段的作用,可用图2-12(b)所示的简支梁上相应的荷载来代替(梁段端截面上的剪力可由梁的支反力提供,故图中未画出)。
4.4.5 用区段叠加法作静定梁的内力图解析

【例 9.11】简支梁受荷载P和q作用如图9.22(a)所示。试用叠加法画梁的弯矩
【解】将作用在梁上的荷载分为P与q两组。 先分别画出P、q单独作用下的弯矩图,如图9.22(b)、(c)所示。然后将这
两个弯矩图的相应纵坐标叠加起来,如图9.22(a)所示,就是简支梁在集中荷 载P和均布荷载q
【例 9.12】外伸梁受荷载作用如图9.23(a)所示,试用叠加法画梁的弯矩图。
用在简支梁上时的弯矩图,为此必须先求出MA 和MB。
区段叠加法画弯矩图的具体步骤如下:
▲ 首先把杆件分成若干段,求出分段点上的弯矩 值,按比例标在杆件相应的点上,然后每两点间 连以直线。
▲ 如果分段杆件的中间没有荷载作用这直线就是 杆件的弯矩图。如果分段杆件的中间还有荷载作用, 那么在直线上还要叠加上荷载单独在相应简支梁上 产生的弯矩图形。
4.4.5 用区段叠加法作 梁的弯矩图
学习目标:学会用叠加法作内力图
叠加法画弯矩图
根据叠加原理来绘制内力图的方法称为叠加法。 用叠加法画弯矩图,绘图时先把作用在梁上的 复杂的荷载分成几组简单的荷载,分别作出各简单 荷载单独作用下的弯矩图,然后将它们相应的纵坐 标叠加,就得到梁在复杂荷载作用下的弯矩图。例 如图9.21(a)、(b)、(c)所示。 用叠加法画弯矩图时,一般先画直线形的弯矩 图,再叠画上曲线形的弯矩图。
图9.23
二、用区段叠加法画弯矩图
对图示简支梁把其 中的AB段取出,其隔 离体如图所示:
把AB隔离体与相 应的简支梁作一对 比:
Fp
q
A
L
q
MA
A
FQAB
q MA
显然两者是完全
A
相同的。
MA
A
材料力学第五章

Mechanics of Materials 编制:邹思敏 审定:袁海庆
配套教材: 武汉理工大学出版社《材料力学》第三版
(主编 袁海庆)
5
弯曲内力
编制:邹思敏 审定:袁海庆
配套教材: 武汉理工大学出版社《材料力学》第三版 (主编 袁海庆)
5
弯曲内力
5.1 梁的平面弯曲 梁的计算简图 5.2 梁的内力 剪力和弯矩 5.3 剪力方程与弯矩方程 剪力图与弯矩图 5.4 内力与分布荷载间的关系及其应用 5.5 用区段叠加法作梁的弯矩图
y
A
m
n
x B q(x)
x
m n
dx
M(x)+dM(x)
q( x)dx dFQ ( x)
M ( x)
O1
dFQ x q x dx
FQ(x) dx
FQ(x)+dFQ(x) q(x)
5.4.1 剪力、弯矩与分布荷载集度间的关系
对n-n截面形心O1取矩,有
y
A
m
n
m
O1
0 ,
x B q(x)
FQ
二、弯曲内力的正负号规定: 剪力FQ :
FQ dl
+
FQ FQ
-
FQ
以使脱离体有顺时针旋转趋势为正
二、弯曲内力的正负号规定:
弯矩M:
+
M M
-
M
M
以使梁下部纤维受拉为正 为了与后续课程结构力学取得一致,规定弯矩 图要画在梁纤维受拉的一面,可以不标正负号。
例5.1 求简支梁C,B截面的内力。
M 直线 (一般为斜直线) 图 特 征
Me
C
利用以上特征
叠加法绘制弯矩图-PPT

AX l
B
F
叠加法——用叠加原理绘制弯矩图的方法
叠加时,易先画直线形的弯矩图,再叠加曲线形或折线形 的弯矩图
由于剪力图比较好画,重点介绍用叠加法画弯矩图
步骤: 注意:
1. 荷载分解 2. 作分解荷载的弯矩图
3. 叠加作荷载共同作用下 的弯矩图
弯矩图的叠加, 不是两个图形的简单叠加, 而是对应点处纵坐标的相加。
叠加法绘制弯矩图
重点
1、叠加法绘制弯矩图 2、区段叠加法绘制弯矩图。
难点
区段叠加法绘制弯矩图
叠加原理:
几个载荷共同作用的效果,等于各个载荷单独作用效果之和
“效果”——指载荷引起的反力、内力、应力或变形
“之和”——代数和
叠加原理成立的前提条件:小变形条件
q
MxFxqx2
2
M x M 1 x M 2 x
kN
190 160
kNm
210 280
340
4
-
大家有疑问的,可以询问和交流
可以互相讨论下,但要小声点
MA A
MA
q
MB
B
lபைடு நூலகம்
q
A
l
+
+
MB
1/8qL2
1/8qL2
MA BA
l
+
MA
MB B
MB
区段叠加法——用叠加法作某一段梁弯矩图的方法 原理
任意段梁都可以当作简支梁,并可以利用叠加法来作该段梁 的弯矩图
梁分一段: A端截面弯矩:M=MA B端截面弯矩:M=MB
各控制面弯矩分别为:
MA=-12KN MD=8KN MB=-4KN
6KN q=2KN/m
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F
x
F, q 作用该截面上的弯矩等于F, q 单独作 用该截面上的弯矩的代数和
q
qx M ( x ) Fx 2
2
x
3
(Internal forces in beams)
F
q
2 ql 6
+
2l/3
2 ql 81
M F ( x ) Fx
+
x l
Fl
F
2
ห้องสมุดไป่ตู้
qx M q ( x) 2
2 ql 6
1
(Internal forces in beams)
三、步骤 (Procedure)
(1)分别作出各项荷载单独作用下梁的弯矩图;
(2)将其相应的纵坐标叠加即可(注意:不是图形的简单拼凑) 例16 悬臂梁受集中荷载 F 和均布荷载 q 共同作用, 试按叠加 原理作此梁的弯矩图. F=ql/3 q
x
F2 F1 F3
a
122
a
a
a
d
a
+
c
d
a
c
b
e
d
a
c
b
5 215
e
b
e 291
(Internal forces in beams)
F1
D a A
F2
C B
F3
E
d
a
c
b
e
291 a a c 131 215 291 a a
122
d
a
d
a
1 1 M C ( 291 ) 122 ( 215 ) 131kN m 2 2
FS (F1 ,F2 , ,Fn ) = FS (F1 ) + FS ( (F2 ) + + FS (Fn )
M (F1 , F2 , , Fn ) M (F1 ) M (F2 ) M (Fn )
二、适用条件 (Application condition)
所求参数(内力、应力、位移)与荷载满足线性关系. 即在 弹性限度内并满足胡克定律时适用.
+
c b e c
d
b
e
b
e
215
6
2 ql 2
x
q
x
4
l/3
(Internal forces in beams)
例题17 图示一外伸梁,a = 425mm , F1
D
a
F2
A C B
F3
E
F1、 F2 、 F3 分别为 685 kN, 575 kN,
506 kN. 试按叠加原理作此梁的弯矩图 ,求梁的最大弯矩.
a
a
a
解:将梁上荷载分开
l
2
(Internal forces in beams)
解: 悬臂梁受集中荷载 F 和均布荷载 q 共同作用,
在距左端为 x 的任一横截面上的弯矩为 F=ql/3
qx M ( x ) Fx 2
2
q
F 单独作用 M F ( x ) Fx q单独作用
x
2
l
qx M q ( x) 2
(Internal forces in beams)
§4-5 按叠加原理作弯矩图 (Drawing bending-moment diagram by superposition method)
一、叠加原理 (Superposition principle)
多个载荷同时作用于结构而引起的内力等于每个载荷单独 作用于结构而引起的内力的代数和.
