三角函数图像变换
三角函数图形的变换

1.5函数sin()y A x ωϕ=+的图像(第二课时)学习目标:通过本节课的学习,进一步增强对sin y x =的图像与sin()y A x ωϕ=+的图像之间的变换关系及ϕ,ω,A 对sin()y A x ωϕ=+的图像的影响,掌握参数ϕ,ω,A 的影响。
自主学习:1.图象变换:函数y =A sin(ωx +φ) (A >0,ω>0)的图象可由函数y =sin x 的图象作如下变换得到: (1)y =sin x →y =sin(x +φ),把y =sin x 图象上所有的点向____(φ>0)或向____(φ<0)平行移动__________个单位.(2)y =sin (x +φ)→y =sin(ωx +φ),把y =sin(x +φ)图象上各点的横坐标____(0<ω<1)或____(ω>1)到原来的________倍(纵坐标不变).(3)y =sin (ωx +φ)→y =A sin(ωx +φ),把y =sin(ωx +φ)图象上各点的纵坐标______(A >1)或______(0<A <1)到原来的____倍(横坐标不变). 2.当函数y =A sin(ωx +φ) (A >0,ω>0),x ∈(-∞,+∞)表示一个振动量时,则____叫做振幅,T =________叫做周期,f =______叫做频率,________叫做相位,____叫做初相.函数y =A cos(ωx +φ)的最小正周期为____________.y =A tan(ωx +φ)的最小正周期为________.我的疑问:合作探究:探究一:将函数sin y x =的图象上各点向左平行移动3π个单位长度,再把所得图象上所有点的横坐标缩短到原来的12倍,纵坐标不变,再把所得图象上所有点纵坐标伸长到原来的3倍,横坐标不变,求所得图象的解析式。
探究二:已知函数f(x)=Asin(ωx +φ)(A >0,ω>0,|φ|<π2,x ∈R )的图象的一部分如图所示.求函数f (x )的解析式.探究三.求函数3sin 21,3y x π⎛⎫=-+ ⎪⎝⎭()x R ∈的最大值、最小值和最小正周期,并求这个函数取最大值、最小值的x 值的集合。
三角函数的图像变换

cosθ = 邻边/斜边,在单位圆中表示为x坐标。
正切函数(tangent)
三角函数的周期性
tanθ = 对边/邻边,表示为正弦与余弦之比。
正弦、余弦函数周期为2π,正切函数周期为 π。
三角函数在各象限表现
第一象限
所有三角函数值均为正。
第三象限
正弦、余弦函数值为负,正切函数值为正。
第二象限
正弦函数值为正,余弦、正切函数值为负。
伸缩变换对正弦函数影响
横向伸缩
改变正弦函数图像的周期长度。缩小周期使得函数图像更加紧密,扩大周期则 使得函数图像更加稀疏。
纵向伸缩
改变正弦函数图像的振幅大小。增大振幅使得函数图像波动范围更大,减小振 幅则使得函数图像波动范围更小。
周期性与相位调整方法
周期性调整
通过改变正弦函数的周期来调整图像的疏密程度。可以通过调整函数中的系数来 实现周期的变化。
相位调整
通过改变正弦函数的相位来调整图像出现的位置。可以通过在函数中添加常数项 来实现相位的调整。同时,利用三角函数的和差化积公式,也可以实现相位的调 整。
03 余弦函数图像变换分析
余弦函数基本图像特征
波形图像
余弦函数图像呈现周期性波动,具有典型的波形 特征。
振幅和周期
余弦函数的振幅和周期是确定其图像形状和尺寸 的关键参数。
拓展:其他类型周期函数图像变换
锯齿波和方波
除了正弦波和余弦波外,还有其 他类型的周期函数如锯齿波和方 波等,它们的图像变换同样具有 实际应用价值。
周期函数的合成与分解
通过三角函数的线性组合可以合 成其他类型的周期函数;反之, 其他类型的周期函数也可以通过 傅里叶级数展开成三角函数的线 性组合。
三角函数图像变换

左移(ψ>0)或 右移(ψ<0) │ψ│
Y=Sin(X+ψ),
例1
作函数 y = 3sin(2x+ )的简图 3
分析 : 因为T=,所以用“五点法”先作长度为一个周期的 闭区
间上的简图 X 3 设:X 2 x 那么: 3 sin( 2 x ) 3 sin X 且 x 3 2 3
Y=Sin(X+ψ),
3. 周期变换:
Y=SinX
4. 平移变换:
Y=SinX
练习
1. 画出函数Y=Sin(2X+
Y
4 周期的闭区间上的简图。
1
),X∈R在长度为一个
8
-1
O
8
3 8
5 8
7 8
X
左移π/2个单位长度 2.将y=SinX的图象_____________________
方法1:先平移后伸缩演示
y
3 2 1
y=3sin(2x+ )③ 3
y=sinx
3
5 6
o
5 3
2
3
6
x
-1
-2 -3
y=sin(x+ )① 3 y=sin(2x + )② 3
三角函数图像的变换

三角函数图像的变换一.x y sin =图像的三种变换:①函数x y sin =的图象上所有点向左(右)平移ϕ个单位长度,得到函数()sin y x ϕ=+的图象;再将函数()sin y x ϕ=+的图象上所有点的横坐标伸长(缩短)到原来的1ω倍(纵坐标不变),得到函数()sin y x ωϕ=+的图象;再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长(缩短)到原来的A 倍(横坐标不变),得到函数()sin y x ωϕ=A +的图象. ②数sin y x =的图象上所有点的横坐标伸长(缩短)到原来的1ω倍(纵坐标不变),得到函数sin y x ω=的图象;再将函数sin y x ω=的图象上所有点向左(右)平移ϕω个单位长度,得到函数()sin y x ωϕ=+的图象;再将函数()sin y x ωϕ=+的图象上所有点的纵坐标伸长(缩短)到原来的A 倍(横坐标不变),得到函数()sin y x ωϕ=A +的图象. 二.函数()()sin 0,0y x ωϕω=A +A >>的性质: ①振幅:A ;②周期:2πωT =;③频率:12f ωπ==T ;④相位:x ωϕ+;⑤初相:ϕ. 函数()sin y x ωϕ=A ++B ,当1x x =时,取得最小值为min y ;当2x x =时,取得最大值为max y ,则()max min 12y y A =-,()max min 12y y B =+,()21122x x x x T=-<.三.练习1.已知简谐运动()2sin()()32f x x ππϕϕ=+<的图象经过点(0,1),则该简谐运动的最小正周期T =_________;初相ϕ=__________.2.三角方程2sin(2π-x )=1的解集为_______________________. 3.函数),2,0)(sin(R x x A y ∈π<ϕ>ωϕ+ω=的部分图象如图所示,则函数表达式为______________________.{2,}3x x k k Z ππ=±∈ )48sin(4π+π-=x y第3题4.要得到函数sin y x =的图象,只需将函数cos y x π⎛⎫=- ⎪3⎝⎭的图象向右平移__________个单位.5.为了得到函数R x x y ∈+=),63sin(2π的图像,只需把函数2sin y x =,x R ∈的图像上所有的点①向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变);②向右平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变);③向左平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变); ④向右平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变).其中,正确的序号有_____③______. 6.为了得到函数)62sin(π-=x y 的图象,可以将函数x y 2cos =的图象向右平移__3π__个单位长度.7.若函数()2sin()f x x ωϕ=+,x ∈R (其中0ω>,2ϕπ<)的最小正周期是π,且(0)f =ω=______;ϕ=__________.8.下列函数: ①sin 6y x π⎛⎫=+⎪⎝⎭; ②sin 26y x π⎛⎫=-⎪⎝⎭; ③cos 43y x π⎛⎫=-⎪⎝⎭; ④cos 26y x π⎛⎫=-⎪⎝⎭. 其中函数图象的一部分如右图所示的序号有_____④_____. 9.函数y =sin(2x +3π)的图象关于点_______________对称. 10.求下列函数的单调减区间: (1)⎪⎭⎫⎝⎛+=62cos 2πx y (2)⎪⎭⎫ ⎝⎛+-=32sin 2πx y 11. 函数tan()2y x π=-(44x ππ-≤≤且0)x ≠的值域是___________________12. 7.如图,函数π2cos()(00)2y x x >ωθωθ=+∈R ,,≤≤的图象与y轴相交于点(0,且该函数的最小正周期为π.(1)求θ和ω的值;π6第8题(2)已知点π2A⎛⎫⎪⎝⎭,,点P是该函数图象上一点,点00()Q x y,是PA当y=ππ2x⎡⎤∈⎢⎥⎣⎦,时,求x的值.13.设函数)(),()2sin()(xfyxxf=<<-+=ϕπϕ图像的一条对称轴是直线8π=x.(Ⅰ)求ϕ;(Ⅱ)求函数)(xfy=的单调增区间;(Ⅲ)画出函数)(xfy=在区间],0[π上的图像第7题。
三角函数图形的变换
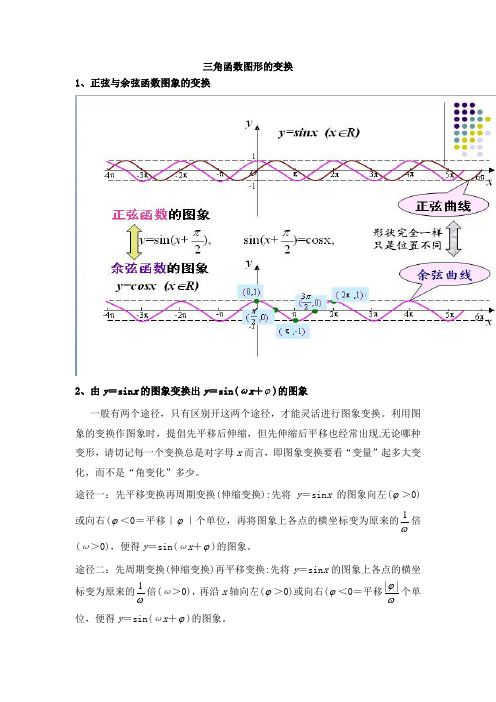
三角函数图形的变换1、正弦与余弦函数图象的变换2、由y =sin x 的图象变换出y =sin(ωx +ϕ)的图象一般有两个途径,只有区别开这两个途径,才能灵活进行图象变换。
利用图象的变换作图象时,提倡先平移后伸缩,但先伸缩后平移也经常出现无论哪种变形,请切记每一个变换总是对字母x 而言,即图象变换要看“变量”起多大变化,而不是“角变化”多少。
途径一:先平移变换再周期变换(伸缩变换):先将y =sin x 的图象向左(ϕ>0)或向右(ϕ<0=平移|ϕ|个单位,再将图象上各点的横坐标变为原来的ω1倍(ω>0),便得y =sin(ωx +ϕ)的图象。
途径二:先周期变换(伸缩变换)再平移变换:先将y =sin x 的图象上各点的横坐标变为原来的ω1倍(ω>0),再沿x 轴向左(ϕ>0)或向右(ϕ<0=平移ωϕ||个单位,便得y =sin(ωx +ϕ)的图象。
作y =sin x (长度为2π的某闭区间)的图象 得y =sin(x +φ) 的图象得y =sin ωx 的图象 得y =sin(ωx +φ) 的图象 得y =sin(ωx +φ) 的图象 得y =Asin(ωx +φ)的图象,先在一个周期闭区间上再扩充到R 上沿x 轴平 移|φ|个单位 横坐标 伸长或缩短 横坐标伸 长或缩短沿x 轴平 移|ωϕ|个单位 纵坐标伸 长或缩短纵坐标伸 长或缩短【经典例题】图像变换一:左右平移1、把函数R x x y ∈=,sin 图像上所有的点向左平移4π个单位,所得函数的解析式为 _________2、把函数R x x y ∈=,cos 图像上所有的点向右平移5π个单位,所得函数的解析式为 _________图像变换二:纵向伸缩3、对于函数R x x y ∈=,s i n 3的图像是将R x x y ∈=,sin 的图像上所有点的______(“横”或”纵”)坐标______(伸长或缩短)为原来的______而得到的图像。
三角函数的图像变换

三角函数b x A y ++=)sin(ϕω的图像变换三角函数的图像变换是历年来高考的重点内容,因此我们有必要对这一问题作一下研究。
下面就三角函数的图像变换的基本题型,做以详细讲析:一、 振幅变换由函数)(x f y =的图像变换为)(x Af y =的图像,其主要的方法是将)(x f y =图像上的各点的纵坐标变为原来的A 倍,即)()(A x Af y x f y =−−−−−−→−=倍纵坐标变为原来的。
例1、要得到)32sin(4π-=x y 的图像,只需将)32sin(π-=x y 的图像( )。
A 、 向上平移4个单位;B 、 将)32sin(π-=x y 图像上的各点的纵坐标变为原来的4倍; C 、 将)32sin(π-=x y 图像上的各点的纵坐标变为原来的4-倍; D 、 向下平移4个位单位。
分析:由题意可知,将)32sin(π-=x y 图像上的各点的纵坐标变为原来的4倍,就可以得到)32sin(4π-=x y 的图像。
故选B 。
二、 周期变换由函数)(x f y =的图像变换为)(x f y ω=的图像,其主要的方法是将)(x f y =图像上的各点的横坐标变为原来的ω1倍,即)()(1x f y x f y ωω=−−−−−−→−=倍横坐标变为原来的。
例2、如何由x y sin =的图像得到x y 2sin 2=的图像。
解:由x y sin =的图像上各点的纵坐标伸长到原来的2倍,得到x y sin 2=的图像,再将x y sin 2=的图像各点的横坐标压缩为原来的21倍,得到x y 2sin 2=的图像。
三、 相位变换(左右平移变换)由函数)(x f y =的图像变换为)(ϕ+=x f y 的图像,其主要的方法是将)(x f y =图像上所有点向左或向右平移ϕ个单位。
即)()(0)(ϕϕϕ+=−−−−−−→−=>x f y x f y 个单位向左平移 )()(0)(ϕϕϕ-=−−−−−−→−=>x f y x f y 个单位向右平移 例3、如何由)32sin(31π+=x y 的图像得到x y sin =的图像。
1.3.3三角函数图像变换

方法1: (按 , , A顺序变换 )
y
y sin x
3
2
y=3sin(2x+ ) 3
y 3 sin(2 x ) 3
1
y=sinx
3
5 6
6
o
-1
3
5 3
2
x
-2
y=sin2x y=sin(2x+ ) 3
-3
方法2:(按 , , A顺序变换 )
已知函数f ( x) A sin(x )( 0, | |
2
)的图象与y轴
3 交于点(0, ), 它与y轴右侧的第一个最大值点和最小值点 2 分别是( x0 ,3), ( x0 2 ,3)
(1)求函数y f ( x)的解析式; (2)用“五点法”作此函数在一个周期内的图象; (3)说明它是由函数y sin x的图象经过哪些变换得到的?
y 3 sin(x ) 6
小结:
1、作函数y=Asin(x+) 的图象:
(1)用“五点法”作图。
(2)利用变换关系作图。 2、函数 y = sinx 的图象与函数
y=Asin(x+)的图象间的变换关系。
解 : 因为它与y轴右侧的第一个最大值点和最小值点 分别是( x0 ,3), ( x0 2 ,3),
T 2 x0 2 x0 2 , 所以 1 2 T
y 3 sin(x )
3 又 过点(0, ), 2 3 3 sin , 且 | | 2 2 6
四、课堂练习
1、要得到函数 y sin(2 x ) 的图象, 3 只需要将 y sin 2 x
三角函数图像变换研究

图像变换的基本原理和方法
▪ 图像剪切变换
1.定义与实现:图像剪切变换是通过改变图像某些区域的宽度 和高度,使得图像产生倾斜效果。它可以使用仿射变换矩阵来 描述。 2.特性:剪切变换改变了图像的几何结构,但保持了图像的比 例关系。过度的剪切可能使图像变得难以辨认。 3.实际应用:图像剪切变换常用
三角函数图像变换研究
▪ 机器学习与三角函数图像变换的结合研究
1.利用机器学习方法改进三角函数图像变换算法 2.构建基于深度学习的三角函数图像变换模型 3.分析机器学习对三角函数图像变换精度和速度的影响
未来三角函数图像变换的研究方向
▪ 三角函数图像变换在虚拟现实中的应用研究
1.虚拟现实中对三角函数图像变换的需求分析 2.开发适用于虚拟现实的三角函数图像变换技术 3.实际应用场景中三角函数图像变换的效果评估
1.定义与实现:图像旋转变换是将图像绕某个点(通常是原点)以一定的角度旋转 。旋转矩阵可用于描述这种变换。 2.特性:旋转变换会改变图像的方向,但保持图像的比例关系不变。非整数倍的旋 转可能会导致图像边缘出现锯齿状。 3.实际应用:图像旋转变换在各种应用场景中都非常常见,如图像内容分类、自动 驾驶车辆导航等。
▪ 变换技巧在图像处理中的应用
1.使用三角函数图像变换进行图像缩放、旋转和平移 2.应用变换方法进行图像增强和降噪处理 3.利用变换技巧实现图像特征提取和识别
变换技巧在实际问题中的应用
▪ 变换技巧在控制理论中的应用
1.利用三角函数图像变换进行系统建模和分析 2.借助变换方法设计控制器以稳定和优化系统性能 3.通过变换实现控制系统的实时监测和故障诊断
▪ 三角函数图像的平移变换
1.平移变换公式 2.图像移动方向的判断 3.平移变换对周期性的影响
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数图像及其变换
一、
知识梳理
1、sin y x =与cos y x =的图像与性质
2、sin y x =与sin()y A x ωφ=+
(1) 形如sin()y A x ωφ=+的函数图像的画法 (2) sin y x =与sin()y A x ωφ=+图像的关系
二、
典型例题
1、把函数sin y x =(x R ∈)的图象上所有点向左平行移动3
π
个单位长度,再把所得图象上所有点的横坐标缩短到原来的1
2
倍(纵坐标不变),得到的图象所表示的函数是
(A )sin(2)3y x π=-,x R ∈ (B )sin()26x y π
=+,x R ∈
(C )sin(2)3y x π=+,x R ∈ (D )sin(2)3
2y x π
=+,x R ∈
2、为得到函数πcos 23y x ⎛
⎫=+ ⎪⎝⎭的图像,只需将函数sin 2y x =的图像( )
A .向左平移
5π
12个长度单位 B .向右平移
5π
12个长度单位 C .向左平移5π
6
个长度单位
D .向右平移5π
6
个长度单位
3、函数πsin 23y x ⎛⎫=-
⎪⎝
⎭在区间ππ2⎡⎤-⎢⎥⎣⎦
,的简图是( )
4、下面有五个命题:
①函数y =sin 4x -cos 4x 的最小正周期是π. ②终边在y 轴上的角的集合是{a |a =
Z k k ∈π
,2
|. ③在同一坐标系中,函数y =sin x 的图象和函数y =x 的图象有三个公共点. ④把函数.2sin 36
)32sin(3的图象得到的图象向右平移x y x y =π
π+= ⑤函数.0)2
sin(〕上是减函数,在〔ππ
-
=x y 其中真命题的序号是 (写出所言 )
5、将函数3sin()y x θ=-的图象向右平移3
π
个单位得到图象F ',若F '的一条对称轴是直线4
x π
=,则θ的一个可能取值是
A.
π125 B. π125- C. π12
11 D. 1112π-
三、高考再现
1、已知函数2
π()sin
sin 2
f x x x x ωωω⎛⎫
=++ ⎪⎝
⎭
(0ω>)的最小正周期为π.
(Ⅰ)求ω的值;(Ⅱ)求函数()f x 在区间2π03⎡⎤⎢⎥⎣⎦
,上的取值范围.
2、已知函数()cos(2)2sin()sin()344
f x x x x π
ππ
=-
+-+ (Ⅰ)求函数()f x 的最小正周期和图象的对称轴方程 (Ⅱ)求函数()f x 在区间[,]122
ππ
-上的值域
3、已知函数f (x )=)0,0)(cos()sin(3><<+-+ωϕϕωϕωπx x 为偶函数,且函数y =f (x )图象的两相邻对称轴间的距离为.2
π (Ⅰ)求f (
8
π
)的值; (Ⅱ)将函数y =f (x )的图象向右平移
6
π
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y =g (x )的图象,求g (x )的单调递减区间.
自我检测
1为得到函数πcos 23y x ⎛⎫
=+ ⎪⎝
⎭
的图像,只需将函数sin 2y x =的图像 A .向左平移
5π
12个长度单位 B .向右平移
5π
12个长度单位 C .向左平移5π
6个长度单位
D .向右平移5π
6
个长度单位
2. 函数)0,0)(cos()(>>+=ωϕωA x A x f 的部分图象如图所示,则
+++)3()2()1(f f f )2009(f + 的值为
A .2
B .22-
C .7
D .0
3、已知函数f (x )=sin 2x+3sinxcosx+2cos 2x ,x ∈R . (1)求函数f (x )的最小正周期和单调增区间;
(2)函数f (x )的图象可以由函数y=sin2x (x ∈R )的图象经过怎样的变换得到?。
