主成分分析及R语言案例
利用R语言主成分分析优化产品质量控制策略研究

利用R语言主成分分析优化产品质量控制策略研究近年来,随着科技的发展和市场竞争的加剧,企业对于产品质量的要求越来越高。
为了满足这一需求,许多企业开始探索如何利用数据分析的方法来优化产品质量控制策略。
在这个任务中,我们将利用R语言进行主成分分析,以优化产品质量控制策略为研究目标。
首先,让我们对主成分分析(Principal Component Analysis,简称PCA)进行简要介绍。
PCA是一种多变量数据分析方法,通过降维、提取主要信息并去除冗余信息,从而实现数据特征的压缩和可视化。
在产品质量控制中,利用PCA可以帮助我们找到影响产品质量的关键因素,并构建合适的质控策略。
下面,我们将按照以下步骤进行利用R语言进行主成分分析优化产品质量控制策略的研究:1. 数据收集和预处理在开始主成分分析之前,需要收集产品质量相关的数据。
这些数据可以包括产品的各种物理特性、生产工艺参数、原材料成分等。
将这些数据整理成一个数据矩阵,并进行数据清洗和预处理,如缺失值处理、异常值处理和数据标准化等,以确保数据的准确性和可靠性。
2. 主成分分析模型构建利用R语言中的主成分分析函数,我们可以对数据进行主成分分析。
首先,需要导入相应的R包,如“stats”和“psych”,以便使用主成分分析函数。
然后,利用主成分分析函数对数据进行分析和建模,并提取主成分。
3. 解释主成分主成分分析的结果包括主成分的贡献率和载荷矩阵。
贡献率表示每个主成分解释原始数据方差的比例,载荷矩阵是各个主成分与原始变量之间的相关系数矩阵。
通过解释主成分,我们可以确定哪些主成分对于产品质量的影响最大。
4. 选取主成分根据主成分的贡献率,我们可以决定保留几个主成分来解释整个数据集的方差。
常用的选择方法包括保留贡献率大于某个阈值(如80%)的主成分或根据Kaiser准则选择所有贡献率大于1的主成分。
选取主成分的目的是降低数据的维度,以便后续分析和应用。
5. 构建质量控制策略基于选取的主成分,我们可以通过建立质量控制模型来优化产品质量控制策略。
【原创】R语言主成分分析因子分析案例报告(完整附数据)

R语言主成分分析因子分析案例报告R语言多元分析系列之一:主成分分析主成分分析(principal components analysis,PCA)是一种分析、简化数据集的技术。
它把原始数据变换到一个新的坐标系统中,使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上,第二大方差在第二个坐标(第二主成分)上,依次类推。
主成分分析经常用减少数据集的维数,同时保持数据集的对方差贡献最大的特征。
这是通过保留低阶主成分,忽略高阶主成分做到的。
这样低阶成分往往能够保留住数据的最重要方面。
但是在处理观测数目小于变量数目时无法发挥作用,例如基因数据。
R语言中进行主成分分析可以采用基本的princomp函数,将结果输入到summary和plot函数中可分别得到分析结果和碎石图。
但psych扩展包更具灵活性。
1 选择主成分个数选择主成分个数通常有如下几种评判标准:∙根据经验与理论进行选择∙根据累积方差贡献率,例如选择使累积方差贡献率达到80%的主成分个数。
∙根据相关系数矩阵的特征值,选择特征值大于1的主成分。
另一种较为先进的方法是平行分析(parallel analysis)。
该方法首先生成若干组与原始数据结构相同的随机矩阵,求出其特征值并进行平均,然后和真实数据的特征值进行比对,根据交叉点的位置来选择主成分个数。
我们选择USJudgeRatings数据集举例,首先加载psych包,然后使用fa.parallel函数绘制下图,从图中可见第一主成分位于红线上方,第二主成分位于红线下方,因此主成分数目选择1。
fa.parallel(USJudgeRatings[,-1], fa="pc",n.iter=100, show.legend=FALSE)2 提取主成分pc=principal(USJudgeRatings[,-1],nfactors=1)PC1 h2 u21 0.92 0.84 0.15652 0.91 0.83 0.16633 0.97 0.94 0.06134 0.96 0.93 0.07205 0.96 0.92 0.07636 0.98 0.97 0.02997 0.98 0.95 0.04698 1.00 0.99 0.00919 0.99 0.98 0.019610 0.89 0.80 0.201311 0.99 0.97 0.0275PC1SS loadings 10.13Proportion Var 0.92从上面的结果观察到,PC1即观测变量与主成分之间的相关系数,h2是变量能被主成分解释的比例,u2则是不能解释的比例。
R语言主成分分析实例和代码

R语言进行主成分分析实例1、基于princomp函数进行实例说明:(中学生身体四项指标的主成分分析)在某中学随机抽取某年级30名学生,测量其身高(X1)、体重(X2)、胸围(X3)和坐高(X4),数据如下。
试对这30名中学生身体四项指标数据做主成分分析将上面这些数据保存在students_data.csv中data <- read.csv('D:/students_data.csv', header = T)注:header = T表示将students_data.csv中的第一行数据设置为列名,这种情况下,students_data.csv中的第二行到最后一行数据作为data中的有效数据。
header = F表示不将students_data.csv中的第一行数据设置为列名,这种情况下,students_data.csv 中的第一行到最后一行数据作为data中的有效数据。
第二步:进行主成分分析student.pr <- princomp(data, cor = T)注:cor = T的意思是用相关系数进行主成分分析。
Screeplot(student.pr,type=”line”,main=”碎石图”,lwd=2)第三步:观察主成分分析的详细情况summary(student.pr, loadings = T)执行完这一步的具体结果如下:说明:结果中的Comp.1、Comp.2、Comp.3和Comp.4是计算出来的主成分,Standard deviation代表每个主成分的标准差,Proportion of Variance代表每个主成分的贡献率,Cumulative Proportion代表各个主成分的累积贡献率。
每个主成分都不属于X1、X2、X 3和X4中的任何一个。
第一主成分、第二主成分、第三主成分和第四主成分都是X1、X2、X3和X4的线性组合,也就是说最原始数据的成分经过线性变换得到了各个主成分。
【原创】R语言城镇居民人均消费数据主成分,聚类分析报告.pdf(附代码数据)

有问题到百度搜索“大数据部落”就可以了欢迎登陆官网:/datablog我国城镇居民人均消费支出研究有问题到百度搜索“大数据部落”就可以了欢迎登陆官网:/datablog摘要:近年来,随着我们经济的快速发展,居民的消费结构也发生了巨大变化,人们开始根据自身的需求选择多种多样的商品,而且人们在实现物质需求满足的同时,还在不断追求精神需求的满足。
对此,本文先使用R语言对城镇居民人均总消费支出以及恩格尔系数的总体现状进行数据可视化,接着运用主成分和聚类分析法对我国31个省级行政区(不含港澳台)城镇居民消费结构进行综合评价。
共提取2个主成分,分别命名为日常必需品消费成分、非日常必需品成分,并将31个省区市主成分综合得分进行排名和聚类分析,结果分为四类。
最终得出相关结论,体现不同地区的经济发展、城镇居民消费结构、消费偏好的差异性以及其中的联系。
关键词:城镇居民人均消费;数据可视化;主成分分析;聚类分析有问题到百度搜索“大数据部落”就可以了欢迎登陆官网:/datablog有问题到百度搜索“大数据部落”就可以了欢迎登陆官网:/datablog目录一、引言 (4)1.1研究背景及意义 (4)1.2研究方法及数据来源 (4)二、我国城镇居民人均消费支出现状分析 (5)2.1各地区城镇居民人均总消费支出 (5)2.2恩格尔系数分析 (6)三、城镇居民人均消费支出的统计建模分析 (8)3.1主成分分析 (8)3.1.1计算相关矩阵 (8)3.1.2计算相关矩阵的特征值和主成分负荷 (8)3.1.3确定主成分 (9)3.1.4主成分得分 (9)3.1.5计算主成分C1,C2的系数 (10)3.1.6各省、市、自治区的主成分得分排名 (10)3.1.7主成分作图 (12)3.2聚类分析 (13)3.2.1聚类分析结果分析 (13)四、结论及建议 (16)有问题到百度搜索“大数据部落”就可以了欢迎登陆官网:/datablog附录: (17)―、引言1.1研究背景及意义人均消费支出指居民用于满足家庭日常生活消费的全部支出,包括购买实物支出和服务性消费支出。
R语言的主成分分析包在生物信息学中的应用研究

R语言的主成分分析包在生物信息学中的应用研究主成分分析(Principal Component Analysis,简称PCA)是一种常用的数据分析方法,通过线性变换将原始数据转化为一组互不相关的新变量,以达到降维、提取主要特征、简化模型等目的。
在生物信息学中,R语言的主成分分析包具有广泛的应用,本文将重点介绍其在基因表达数据处理、蛋白质结构分析和微生物群落研究等方面的应用。
一、基因表达数据处理PCA在基因表达数据分析中通常用于降维和可视化,帮助研究人员从大量的基因表达数据中挖掘出相关的生物学信息。
首先,可以利用R语言中的主成分分析包,将基因表达数据转化为主成分得分。
然后,通过绘制二维或三维散点图,观察样本间的相似性和差异性,以及是否存在聚类现象。
此外,还可以通过PCA分析,找出对样本分类起主导作用的基因,从而有针对性地进行后续的生物学实验和分析。
二、蛋白质结构分析蛋白质结构是理解蛋白质功能和相互作用的关键因素之一。
R语言的主成分分析包在蛋白质结构分析中有着广泛的应用。
研究人员可以利用主成分分析包提取蛋白质结构的主要变化因子,从而研究蛋白质的构象动力学特征。
通过对蛋白质结构的主成分分析,可以发现蛋白质结构的变化趋势、蛋白质结构动力学的关键特征,进而解析蛋白质的结构与功能之间的关系。
三、微生物群落研究微生物群落是指在同一生态系统中共生的微生物总体。
对微生物群落的研究有助于揭示微生物的多样性、功能和相互作用。
PCA可以将微生物群落数据的高维空间降低到低维空间,从而方便对微生物群落进行比较和分类。
利用R语言的主成分分析包,可以分析微生物群落数据中的主要成分,并绘制相关的图表和图像,揭示不同样本或实验组之间的差异和相似性。
此外,利用PCA还可以探索微生物群落的物种多样性及其与环境因素的相关性。
四、其他应用除了上述的应用领域,R语言的主成分分析包还可以在其他生物信息学研究中发挥重要作用。
比如在转录因子结合位点分析、基因富集分析、表达定量数据分析、蛋白质组学数据分析等方面。
R语言主成分分析在文本挖掘中的应用探索

R语言主成分分析在文本挖掘中的应用探索主成分分析(Principal Component Analysis,简称PCA)是一种常用的统计分析方法,可以降低数据维度和提取重要特征。
在文本挖掘中,R语言主成分分析可以应用于多个方面,包括文本数据降维、文本分类、文本聚类等。
本文将探索R 语言主成分分析在文本挖掘中的应用。
1. 文本数据向量化文本挖掘首先需要将文本数据向量化,将其转化为数值型矩阵,以便进行主成分分析。
在R语言中,我们可以使用"tm"包和"tidytext"包来进行文本预处理和向量化。
首先,可以使用"tm"包对文本进行词频统计,提取关键词,并创建词袋模型。
然后,使用"tidytext"包将文本转换为词-文档矩阵,其中行代表文档,列代表词,并且每个单元格的值表示对应词在文档中的出现频率。
2. 文本数据降维主成分分析可以通过线性变换将原始的高维数据映射到低维空间,提取出重要的特征。
在文本挖掘中,可以利用主成分分析对文本数据进行降维,以便更好地理解和分析文本。
在R语言中,可以使用"prcomp"函数对文本向量进行主成分分析。
该函数会返回主成分得分和主成分的方差贡献率等信息。
可以通过设定方差贡献率的阈值,选择保留的主成分个数,从而实现文本数据降维。
3. 文本特征提取主成分分析可以从文本数据中提取关键特征,这对于后续的文本分类和聚类任务非常有用。
在R语言中,可以通过获取主成分的贡献度来确定每个主成分所代表的特征。
可以使用"princomp"或"prcomp"函数获取主成分的贡献度,并根据贡献度的大小选择最具代表性的主成分特征。
通过提取主成分的特征,可以帮助理解文本的关键主题、词汇分布等。
4. 文本分类与聚类主成分分析在文本分类和聚类中也有广泛应用。
通过提取文本特征,并利用主成分分析得到的低维表示,可以对文本进行分类和聚类。
主成分分析案例聚类分析案例
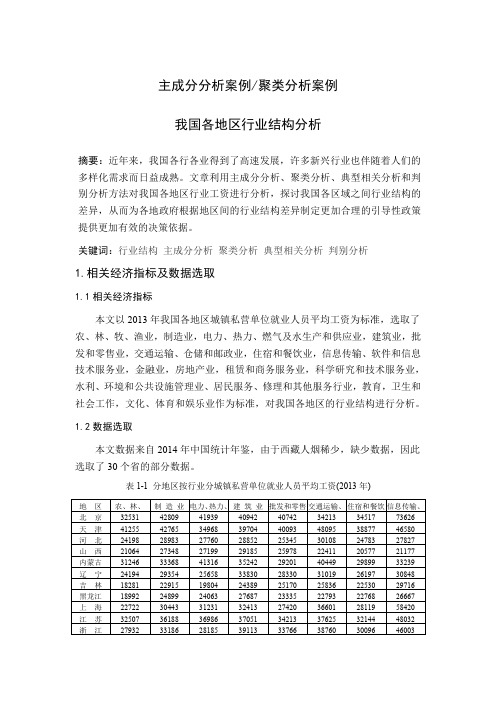
主成分分析案例/聚类分析案例我国各地区行业结构分析摘要:近年来,我国各行各业得到了高速发展,许多新兴行业也伴随着人们的多样化需求而日益成熟。
文章利用主成分分析、聚类分析、典型相关分析和判别分析方法对我国各地区行业工资进行分析,探讨我国各区域之间行业结构的差异,从而为各地政府根据地区间的行业结构差异制定更加合理的引导性政策提供更加有效的决策依据。
关键词:行业结构主成分分析聚类分析典型相关分析判别分析1.相关经济指标及数据选取1.1相关经济指标本文以2013年我国各地区城镇私营单位就业人员平均工资为标准,选取了农、林、牧、渔业,制造业,电力、热力、燃气及水生产和供应业,建筑业,批发和零售业,交通运输、仓储和邮政业,住宿和餐饮业,信息传输、软件和信息技术服务业,金融业,房地产业,租赁和商务服务业,科学研究和技术服务业,水利、环境和公共设施管理业、居民服务、修理和其他服务行业,教育,卫生和社会工作,文化、体育和娱乐业作为标准,对我国各地区的行业结构进行分析。
1.2数据选取本文数据来自2014年中国统计年鉴,由于西藏人烟稀少,缺少数据,因此选取了30个省的部分数据。
表1-1 分地区按行业分城镇私营单位就业人员平均工资(2013年)地区农、林、制造业电力、热力、建筑业批发和零售交通运输、住宿和餐饮信息传输、北京32531 42809 41939 40942 40742 34213 34517 73626 天津41255 42765 34968 39704 40093 48095 38877 46580 河北24198 28983 27760 28852 25345 30108 24783 27827 山西21064 27348 27199 29185 25978 22411 20577 21177 内蒙古31246 33368 41316 35242 29201 40449 29899 33239 辽宁24194 29354 25658 33830 28330 31019 26197 30848 吉林18281 22915 19804 24389 25170 25836 22530 29716 黑龙江18992 24899 24063 27687 23335 22793 22768 26667 上海22722 30443 31231 32413 27420 36601 28119 58420 江苏32507 36188 36986 37051 34213 37625 32144 48032 浙江27932 33186 28185 39113 33766 38760 30096 46003安徽21159 31943 26903 35024 27437 38871 27810 21489 福建30234 35460 29918 39207 33192 40793 28951 46072 江西25854 26924 31275 32085 25652 29388 22678 30168 山东30394 34705 39881 35392 31817 35833 30311 37675 河南19869 23142 23711 27104 23086 24919 21798 22215 湖北17742 25696 26030 27611 23028 23379 23694 33526 湖南23363 27287 32001 29932 23271 25321 23264 35898 广东25709 35646 21670 37488 40866 41074 29401 61935 广西22762 29315 27879 30752 25026 28395 24300 26484 海南16593 27836 20408 33335 29126 37389 27086 29651 重庆27961 35398 34641 36539 32919 34703 27616 38615 四川25127 29652 30099 30850 29149 29386 26066 28671 贵州18034 27183 43575 26704 22260 23913 21155 35040 云南21580 24646 26405 27603 28732 28718 25552 25011 陕西22480 25582 25193 26140 24392 25359 23418 33454 甘肃19319 24212 24873 25256 26544 25435 18656 25994 青海18363 27676 33502 24730 27760 25290 24295 24681 宁夏24172 31638 32293 36178 28035 30101 28544 29269 新疆30308 32990 33911 41001 27373 37746 24646 312792.主成分分析2.1构造因子变量的前提主成分分析的目的是从众多原有变量中提炼少数具有代表性的因自变量。
基于R语言的主成分分析结果解释及模型选择策略分析

基于R语言的主成分分析结果解释及模型选择策略分析主成分分析(Principal Component Analysis,PCA)是一种常用的降维技术,旨在将高维数据转换成低维度的数据集,同时保留尽可能多的信息。
本文将基于R语言对主成分分析的结果进行解释,并探讨模型选择策略。
首先,我们需要明确主成分分析的基本原理。
主成分分析的核心思想是将原始数据通过线性变换,转换为新的坐标系,使得数据在新的坐标系中具有最大的方差。
这些新的坐标轴称为主成分,每一个主成分都是原始数据的线性组合。
主成分分析的结果包括主成分的解释方差、主成分权重以及主成分的累计解释方差等信息。
在R语言中,我们可以使用prcomp()函数进行主成分分析。
以下是一个示例代码:```R# 导入数据data <- read.csv("data.csv")# 执行主成分分析pca <- prcomp(data, scale = TRUE) # scale参数用于数据标准化# 输出主成分分析的结果summary(pca)```执行以上代码后,我们可以获得主成分分析的结果。
其中,summary(pca)函数会输出每个主成分的解释方差、主成分权重以及主成分的累计解释方差等信息。
通过分析这些信息,我们可以对数据的结构和特点有更深入的了解。
解释主成分分析结果时,一个重要的指标是每个主成分的解释方差。
解释方差指标表示主成分能够解释的原始数据的方差比例。
通常,我们关注解释方差大于1的主成分。
较大的解释方差表明该主成分具有更强的解释能力。
另外,主成分权重也是解释主成分分析结果的关键信息之一。
主成分权重表示每个主成分对原始数据的贡献程度。
具有较大权重的变量在主成分所代表的维度上具有较高的重要性。
在模型选择策略分析方面,我们可以使用累计解释方差图来帮助我们选择主成分数量。
累计解释方差图显示了前n个主成分解释方差的累计总和。
通过观察累计解释方差图,我们可以确定主成分的数量,以保留足够的数据方差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程名称:
统计中的矩阵应用
课程编号: 01SAQ9005
论文题目:
主成分分析及 R 语言案例
研究生姓名:
李腾龙
学号:
13720067
研究生班级: 理学院统计系
论文评语:
成 绩: 评阅日期:
任课教师:
主成分分析及 R 语言案例
摘要:本文目的在于,在基于主成分分析方法的基础上,给出实际操作
二、主成分分析基本原理
2.1 主成分的定义
概念:主成分分析是把原来多个变量划为少数几个综合指标的一种统计分析 方法。从数学角度来看,这是一种降维处理技术。
思路:一个研究对象,往往是多要素的复杂系统。变量太多无疑会增加分析 问题的难度和复杂性,利用原变量之间的相关关系,用较少的新变量代替原来较 多的变量,并使这些少数变量尽可能多的保留原来较多的变量所反应的信息,这 样问题就简单化了。
主成分分析(Principal Component Analysis,PCA),就是将多个变量通过 线性变换以选出较少个数重要变量的一种多元统计分析方法。又称主分量分析。
主成分分析所关心的问题,是通过一组变量的几个线性组合来解释这组变量 的方差-协方差结构,它的一般目的是:(1)数据的压缩;(2)数据的解释。
主成分的方差(信息)贡献率用来反映信息量的大小, ai 为:
第二主成分 = 线性组合 a2 x ,在 a2a2 1和 Cov(a1X ,a2 X ) 0 时,它使 Var(a2 X ) 最大;
第 i 个主成分 = 线性组合 aiX ,在 aiai 1 和 Cov(aiX , ak X ) 0(k i) 时,它 使Var(aiX ) 最大;
2.2 基本结论
原理:假定有 n 个样本,每个样本共有 p 个变量,构成一个 n×p 阶的数据 矩阵,
x11 x12 x1p X来自x21x22
x2
p
xn1
xn2
xnp
记原变量指标为 x1, x2 ,, xp ,设它们降维处理后的综合指标,即新变量为 Y1,Y2 ,,Ym (m p) ,则
Y1 a11x1 a12 x2 a1p x p
结论 8.3:如果 Yi eiX , i 1,2, p 是从协方差矩阵 所得到的主成分,
则
ρYi ,X k
eik i kk
,
i,k 1, 2, , p 是Yi 和 X k 之间的相关系数。
三、主成分分析法的计算步骤
主成分分析的具体步骤如下:
(1)计算协方差矩阵 计算样品数据的协方差矩阵: (sij ) pp ,其中
虽然要求 p 个成分可以再现全系统的变异性,但大部分变异性常常只用少数 k 个主成分就可以说明。出现这种情况时,这 k 个主成分中所包含的信息和那 p 个原变量所包含的(几乎)一样多。于是这 k 个主成分就可以用来取代那初试的 p 个变量,并且由对 p 个变量的 n 次测量值所组成的原始数据,就压缩为对 k 个 主成分的 n 次测量值所组成的数据集。
结论 8.1:设 是随机向量 X [ X1, X 2 , X p ] 的协方差矩阵,他有特征值— 特征向量 (1,e1),(2,e2 ),,(p ,ep ) ,其中 1 2 p ,则第 i 个主成分由
Yi eiX ei1X1 ei2 X 2 eip X p , i 1,2, p
给出,此时:Var(Yi ) eiei i
i 1,2,, p
Cov(Yi ,Yk ) eiek 0 i k
如果有某些 i 相等,那么对应的系数向量 ei 的选取从而 i 的选取,就都不是唯一 的了。
结论 8.2:随机变量 X X1 X 2 X p 具有协方差矩阵 ,其特征值-
特征向量为 (1,e1),(2,e2 ),,(p ,ep ) ,其中 1 2 p 0 ,设第 i 个主成 分为Yi eiX , i 1,2, p
p
p
则总体总方差 11 22 pp Var( X i ) 1 2 p Var(Yi )
i1
i1
从而有:
总k个方主差成中分属的于比第例
1
k 2
p
k 1,2,, p
如果总方差的相当大的部分归因于第一个、前两个或前三个主成分,而 p 较大, 那么这些成分就可以“取代”原来的 p 个变量,而且信息损失不多。
中主成分分析方法的具体步骤,并同时叙述了作者对主成分分析的一些 想法和心得。更重要的是,通过本次论文的学习,更加深入地学习了统 计中的矩阵应用的相关知识点,并通过一个案例分析,使自己能够初步 了解并掌握 R 语言统计分析软件的使用方法。
关键词:主成分分析、R 语言、特征值、特征向量
一、引言
在用统计分析方法研究多变量的课题时,变量个数太多就会增加课题的复杂 性。人们自然希望变量个数较少而得到的信息较多。在很多情形,变量之间是有 一定的相关关系的,当两个变量之间有一定相关关系时,可以解释为这两个变量 反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量,建立 尽可能少的新变量,使得这些新变量是两两不相关的,而且这些新变量在反映课 题的信息方面尽可能保持原有的信息。
Y2
a21 x1
a22 x2
a2 p xp
.......... ..
Ym am1x1 am2 x2 amp x p
主成分是那些不相关的线性组合,Y1,Y2 ,,Ym (m p) ,使他们的方差尽可 能的大。因此我们定义:
第一主成分 = 线性组合 a1X ,在 a1a1 1时,它使Var(a1X ) 最大;
sij
1 n 1
n
( xki
k 1
xi )(xkj
xj)
i, j 1,2, p
(2)计算特征值和特征向量
求出 的特征值 i 及相应的正交化单位特征向量 ai :
解特征方程| I | 0 ,常用雅可比法(Jacobi)求出特征值,并使其按大 小顺序排列 1 2 p 0
的前 m 个较大的特征值 1 2 m 0 ,就是前 m 个主成分对应的方 差,i 对应的单位特征向量 ai 就是主成分Yi 的关于原变量的系数,则原变量的第 i 个主成分Yi 为:Yi aiX
