流体通过颗粒层的流动-小-2-2015-11
流体通过颗粒层的流动

形状不规则的颗粒:
比表面积的定义同上,颗粒的形状及大小分别表示为: (1)颗粒的形状系数(Shape factor):用形状系数表示颗粒的形
状,最常用的形状系数是球形度ψ,它的定义式为
与非球形颗粒体积相等 的球的表面积
非球形颗粒的表面积
标准筛:有不同的系列,其中泰勒(Tyler)
标准筛是较为常用的标准筛之一,其筛孔 的大小以每英寸长度筛网上所具有的筛孔 数目表示,称为目,每个筛的筛网金属丝 的直径也有规定,因此一定目数的筛孔尺 寸一定。例如200目的筛子即指长度为1英 寸的筛网上有200个筛孔。所以筛号越大, 筛孔越小。此标准系列中各相邻筛号(按 从大到小的次序)的筛孔大小按筛孔的净 宽度计以 20.5的倍数递增,即筛孔面积按2 的倍数递增。 筛号(目数):每英寸边长的筛孔数目 筛过量:通过筛孔的颗粒量 筛余量:截留于筛面上的颗粒量
一般颗粒床层的空隙率为0.47~0.7。 测量床层的空隙率的方法:充水法和称量法。
(2)床层的比表面积 单位体积床层中颗粒的表面积称为床层的比表面积。若忽略因颗粒 相互接触而减小的裸露面积,则床层的比表面积αB与颗粒的比表面 积α的关系为: αB= α(1- ε)
影响床层的比表面积的主要因素:颗粒尺寸。一般,颗粒尺寸越小, 床层的比表面积越大。
(2)颗粒群的平均特性参数
颗粒群的平均粒径有不同的表示法,但对于流体 与颗粒之间的相对运动过程,主要涉及流体与颗粒表 面间的相互作用,即颗粒的比表面积起重要作用,因 此通常用等比表面积当量直径来表示颗粒的平均直径, 则混合颗粒的平均比表面积dm。
dm
1 xi
d pi
xi——第i层筛网上颗粒的质量分率 dpi=(di-1+di)/2
华东理工大学网络教育学院《化工原理》专科课程自测题

华东理工大学网络教育学院《化工原理》(专科)课程课件自测题一、流体流动1、机械能守恒自测题1:如图所示,若液面恒定,忽略流动阻力损失,则放水管的出口速度U 与____有关。
(A) H (B) H、d (C) d (D) Pa (E) H、d 、Pa答案:A2、量纲分析法自测题2:量纲分析法的目的在于______。
A 得到各变量间的确切定量关系;B 得到各无量纲数群的确切定量关系;C 用无量纲数群代替变量,使实验与关联工作简化;D 用无量纲数群代替变量,使实验结果更可靠。
答案:C3、流体流动内部结构自测题3:层流与湍流的本质区别是:________。
A)湍流流速>层流流速;B)流道截面大的为湍流,截面小的为层流;C)层流的雷诺数<湍流的雷诺数;D)层流无径向脉动,而湍流有径向脉动。
答案:D4、阻力损失自测题4:图示为一异径管段,从A段流向B段,测得U形压差计的读数为R=R1,从B段流向A段测得U形压差计读数为R=R2 ,若两种情况下的水流量相同,则______。
A)R1>R2;B)R1=R2;C)R1<R2;D)R2=-R1答案:C)自测题5:某液体在内径为d1的管路中稳定流动,其平均流速为u1,当它以相同的体积流量通过某内径为d2(d2=d1/2)的管子时,流速将变为原来的______倍;流动为层流时,管子两端压力降△p f为原来的______倍;湍流时(完全湍流区) △p f为原来的______倍。
A)4;B)16;C)32;D)8答案:A;B;C自测题6:在完全湍流(阻力平方区)时,粗糙管的摩擦系数λ数值________。
A)与光滑管一样;B)只取决于Re;C)只取决于相对粗糙度;D)与粗糙度无关。
答案:C自测题7:如图表明,管中的水处于________。
A)静止; B)向上流动;C)向下流动;D)不一定。
答案:C自测题8:如图,若水槽液位不变①、②、③点的流体总机械能的关系为________。
化工原理第四章流体通过颗粒层的流动

4.4 过滤原理及设备 4.4.1 过滤原理
过滤将固—液两相的悬浮液分离 成滤饼和滤液。 两种过滤方法 滤饼过滤(表面过滤) 颗粒截留在过虑介质表面。适用于较高浓度的悬浮液 架桥现象——对表面过滤,真正起过滤作用的是滤饼本身,
过滤介质仅给架桥现象提供条件 深层过滤 颗粒靠静电力、表面力吸附于过滤。 介质内部。 适用于低浓度、细颗粒的分离
(2)q与τ的关系;
(3)K与τ的关系;
由 q K c, K
2(q qe ) q c 得K 2c2 2qec
(4)ΔP 与τ的关系。 K
必须注意:使用恒速速率 方程时,应使K与τ严格 对应。
q
τ
τ
ΔP
qe≠0
τ
qe=0,s=0 τ
ΔP
qe=0
τ
qe≠0,s≠0 30 τ
恒压过滤方程 P c,
C.床层特性的影响 (1)空隙率ε: 空隙率ε对压降ΔP 的影响非常大,反映在 ε的可变性大,可靠性差; ε较小的误差,将引起压降明显的误差 (2)比表面积α ΔP ∝α2,对同形状颗粒,dp↓, α越大↑,hf(ΔP )↑。 例:其他条件不变空隙率ε由0.5降为0.4,单位床层压降 增加2.8倍。
4
则
4 u
Re' a(1 ) 4
u
a1
当Re’<2时,λ=k’/Re’,
k’=5.0
代入得: P k / a2 1 2 u
L
3
上式称为康采尼方程(注意适用条件:层流);
欧根在更宽的Re’范围内,得出: ' 4.17 0.29
代入基本式:
Re'
P
L
4.17
a2
1
流体通过颗粒层的流动

反应器 催化剂颗粒层等概念
以上化工操作中均为流体通过颗粒层的流动,与流体
在管道中的流动相比较:阻力增大,速度分布均一,
流动特点:层流,绕流(因速度慢也称爬流)。
爬流:爬流速度很小,流动很 缓慢,颗粒迎流面与背流面的 流线对称。
颗粒层中流体流动特点:
(1)床截面的流体速度分布均匀,床层两端产生很大压降△P 原因:大量颗粒随机堆积,颗粒对流体的流动造成很大 的阻力
真正的过滤介质:架桥作用 。
滤浆
滤饼 过滤介质
滤液
滤饼过滤
(2)深层过滤——本质不同于表面过滤,是依靠吸附作用。
深层过滤 深层过滤主要用于含固量很少的悬浮液 化工生产广泛使用的是滤饼过滤。
3、过滤介质 织物介质: 滤布滤网(截留颗粒dp:5~6μm) 多孔性固体介质:素瓷、多孔塑料(dp: 1~3μm) 堆积介质: 固体颗粒如砂、木炭、非编织纤维如玻璃纤维 ——用于含固量少的悬浮液
2、颗粒床层的数学模型
ΔP
hf
Le de
u12 2
;Le
L,Le L
常数
ΔP 1
L
u
de、u1
流体在固定床内流动的简化模型
Le Δ P 1
Δ P Le u12 de 2
表观流速(空床流速)u与实际流速 u1 的关系 :
uA
u1 A1
u
u1
A1 A
u1
化简得到单位床层高度压降: Δ P ( 1 )a u2
影 响
2 、空隙率随装填情况而变,
L
同种物料同样方式装填,空隙率未必能重复
第四节 过滤原理及设备
一、过滤 固液分离的常用方法是通过过滤获得清净的液体或
作为产品的固体颗粒 1、过滤原理 利用重力或人为造成的压差使悬浮液通过某种多孔性 过滤介质分离悬浮液。 2、两种过滤方式 (1)滤饼过滤——依靠通道尺度小于颗粒直径,滤饼是
化工原理课件第4章:过滤

ε反映了床层中颗粒堆集的紧密程度,其大小与颗粒的形状、粒度分 布、装填方法、床层直径、所处的位置等有关。 球形:0.26~0.48 乱堆:0.47~0.7
壁效应
化工原理——流体通过颗粒层的流动
ε的测量方法:
充水法: 称量法:
V水
V
V G
p
V
不适于多孔性颗粒
K 2P1s
r0
化工原理——流体通过颗粒层的流动
4.5.2 间歇过滤的滤液量与过滤时间的关系 1. 恒速过滤方程
若Ve=0,则? K虽为变量,但应为τ时刻的过滤常数值。
化工原理——流体通过颗粒层的流动
2. 恒压过滤方程
若Ve=0,则?
若V=Ve ? qe2 K e
q qe 2 K e
求Ve,τe
(1
- 3
)a
ρu 2
P' L
'
(1- )a 3
u2
单位床层高度的压降, Pa
模型参数
化工原理——流体通过颗粒层的流动
4.3.3 模型的检验和模型参数的估计
1. 康采尼(Kozeny)方程
在流速较低, Re'<2时(层流),
'
K' Re'
其中:
Re'
deu1
u a(1 )
实验测得
K ' 5.0
p
p (1)
化工原理——流体通过颗粒层的流动
流入的量=流出的量+累积量
总量衡算: V悬=V LA
固体量衡算: V悬 LA(1 ) 由上两式可得: L q
1
一般,<<, L q 1
颗粒沉降-2-2015-11-小
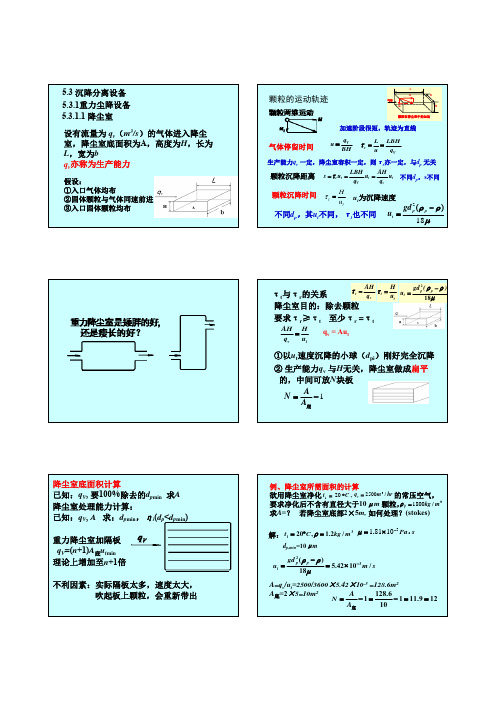
dp,min=10μm
ut =
gd 2 p (ρ p − ρ ) 18 μ
= 5.42 × 10 − 3 m / s
A=qv/ut=2500/3600×5.42×10-3 =128.6m2 A底=2×5=10m2 128.6 A −1 = − 1 = 11.9 = 12 N= 10 A底
5.3 沉降分离设备 5.3.1重力尘降设备 5.3.1.1 降尘室 设有流量为 qv(m3/s)的气体进入降尘 室,降尘室底面积为A,高度为H,长为 L,宽为b qv亦称为生产能力
假设: ①入口气体均布 ②固体颗粒与气体同速前进 ③入口固体颗粒均布
L
颗粒的运动轨迹
u
气体
B H
ut
颗粒在降尘室中的运动
近似性:拟定态处理。 原则上,离心力随半径 是渐增的,沉降在加速。
A r1 r2 O r
B ur C uθ u
颗粒在旋转流场中的运动
5.3.2.1旋风分离器
含尘
B
净化气体
构造:上部为圆筒形下部为圆锥形 A 操作原理: 含尘气体以速度u切向进入旋风分离 器,造成含尘气体在设备内的旋转。 颗粒在惯性离心力的作用下,被抛 至器壁后下滑。 净化气体由升气管排出。
稠浆
= 0.174 kg / s = 628.0 kg / h
(3) t↑ μ↑ 对沉降不利 t↑ ρ↓qm↓
生产能力减小
连续式沉降槽 分离悬浮液 连续加料,清液往上走,稠液往下走, 锥形底部旋转的齿耙把沉渣慢慢移至下部中心, 稠浆从底部出口出去。
5.3.1.3 分级器
陈敏恒《化工原理》(第3版)(上册)章节题库-流体通过颗粒层的流动(圣才出品)

【答案】D
二、填空题 1.影响流体通过固定床的压降的因素有______、______和______,其中影响最大的因素 是______。 【答案】操作变量 u;流体物性μ和ρ;床层特性ε和 a;空隙率ε
2.某板框压滤机,恒压过滤 1 小时得滤液 ,停止过滤用 清水横穿洗涤(清水 粘度与滤液粘度相同),为得到最大生产能力,辅助时间应控制在______小时(过滤介质阻 力忽略不计)。
A.这两种说法都对 B.这两种说法都不对 C.只有第一种说法对 D.只有第二种说法对 【答案】D
14.一定厚度的滤饼对滤液流动的阻力与以下( )因素有关。 A.滤浆的浓度 B.滤液的温度 C.滤液的体积
5 / 37
圣才电子书
D.操作压差
十万种考研考证电子书、题库视频学习平台
4 / 37
圣才电子书 十万种考研考证电子书、题库视频学习平台
D.液体进、出过滤机的压差 【答案】B
12.恒压过滤且介质阻力忽略不计时,如粘度降低 20%,则在同一时刻滤液增加( )。 A.11.8%; B.9.54%; C.20%; D.44% 【答案】A
13.“颗粒的粒度分布越不均匀,则所形成的床层空隙率越大”,“壁附近床层空隙率较 床层中心的空隙率大”,则( )。
【答案】2
12.用压滤机分离悬浮物,忽略过滤介质阻力,滤饼不可压缩,其他条件不变。提高 悬浮液温度,单位过滤时间所得滤液量将______;提高悬浮液的固体含量,单位过滤时间所 得滤液量将______。
2.当介质阻力不能忽略时,过滤所得滤液体积加倍,则( )。 A.过滤速率加倍 B.过滤速率减半 C.过滤速率减小,但速率仍大于原来的一半 D.过滤速率减小且速率小于原来的一半 【答案】C
第4章流体通过颗粒层的流动
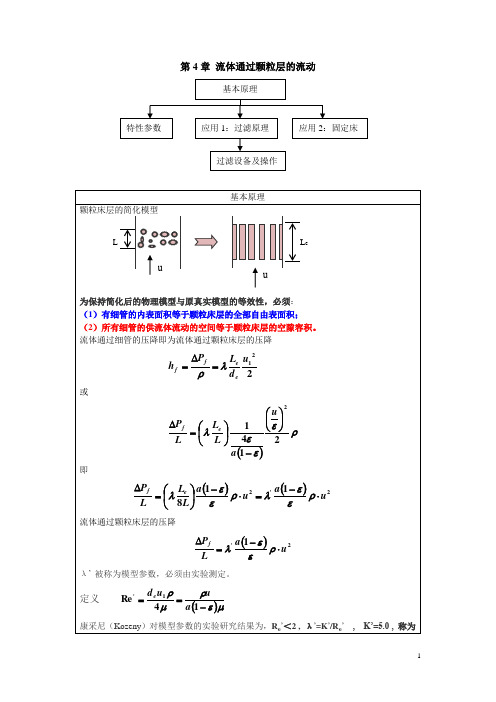
康采尼(Kozeny)对模型参数的实验研究结果为,Re’<2 ,λ’=K’/Re’, K’=5.0 ,称为Kozeny常数。
将模型参数的表达式代入到床层压降的表达式中
欧根(Ergun)在较宽的 范围内, ,获得了关系式
代入到床层压降的表达式中
特性参数
1、颗粒的比表面积
2、颗粒床层的空隙率
3、颗粒床层的比表面积 ,
第4章流体通过颗粒层的流动
基本原理
颗粒床层的简化模型
为保持简化后的物理模型与原真实模型的等效性,必须:
(1)有细管的内表面积等于颗粒床层的全部自由表面积;
(1)
(2)所有细管的供流体流动的空间等于颗粒床层的空隙容积。
流体通过细管的压降即为流体通过颗粒床层的压降
或
即
流体通过颗粒床层的压降
λ’被称为模型参数,必须由实验测定。
单位过滤面积上的滤液体积量
滤饼厚度 、悬浮液中颗粒体积分率 、滤饼空隙率 与单位过滤面积上的滤液体积量 的关系式为
单位过滤面积上过滤速率的表达式则为
定义: , 称为滤饼的比阻。则过滤速率表达式为
或者
考虑过滤介质的阻力后,过滤速率为
令
则
或
定义过滤常数:
自开始即进行恒压过滤,则K为常数,并且 时, ,过滤时间 与累计滤液体积量 (单位面积上累计滤液体积量 )的关系
或
过滤设备及操作
1、板框式压滤机
在保持洗涤水粘度与滤液粘度相同,洗涤操作时的压差与过滤操作时的压差相同时,总面积上的洗涤速率与过滤终了时过滤的速率之间的关系
横穿流洗法, ;置换洗法,
洗涤时间 与过滤时间 的关系
一个生产周期的时间 ,
最佳时间分配:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求出压缩指数s
4.4.4 洗涤速率与洗涤时间
特点:洗涤时推动力、阻力不变,滤饼厚度不再增加,
洗涤速度为常数。
洗涤速度
⎜⎛ ⎝
dV Adτ
⎟⎞ ⎠w
=
洗涤推动力 洗涤阻力
与滤饼厚度、滤饼性质、洗涤液粘度、
①、洗涤速率
介质阻力有关
⎜⎛ dq ⎟⎞ = Δ℘w ⎝ dτ ⎠w rμw (q + qe )φ
则:
τ = V 2 + 2VVe KA 2
τw
=
Vw
⎜⎛ ⎝
dV dτ
⎟⎞ ⎠w
生产能力:
单位时间内获得的滤液量或滤饼量 。
Q= V = V ∑τ τ +τ w +τ D
过滤时间τ越长,是否生产能力越大?
一定的(τw+τD), 必有一个最佳过滤时间τopt
Q= V
= f (τ )
τ +τW +τD
令
某叶滤机恒压操作,过滤终了时V=0.5m3,过 滤时间为1小时。已知
K = 1×10−5 m 2 / s, ve = 0,
求 ①、过滤面积。
②、现在同一压强下洗涤,洗涤液粘度同滤 液的粘度。Vw=0.01m3,求洗涤时间。
③、若将操作压差提高一倍(S=0.3), 其他条件不变,过滤常数K为多少? 获得同样滤液需要多少时间?
K = 2Δ℘ = 2Δ℘1− S
rφμ
r0φμ
操作压强改变后要换算, 悬浮液浓度变化后要换算
在恒压下做实验
过滤某固体悬浮液,压差恒定。20°C下 测得如下数据,试求过滤常数K和qe
过滤时间 τ(s) 单位面积过滤量 q (m3 / m2 )
10
0.01
40
0.02
90
0.03
160
0.04
恒压时: q2 + 2qqe = Kτ τ/q~q 图
求:生产能力 Q = V = ? Στ
解:①由于速度恒定, 则 V∝τ τ(min)= 10 + 10 + 10 ∴ V=4+4+4=12升
② 过滤速率等于洗涤速率,则
dV = V = VW = 0.2V dτ τ τW τW
∴ τW=0.2τ=0.2×30=6min
③ 生产能力
Q
=
τ
V +τW
+τD
求:生产能力
Q
=
V Στ
=?
解:①由恒压方程V2+2VVe=KA2τ τ(min)= 10 + 10 + 10
V =4 + 2 + ? 代入数据求KA2, Ve 42+2×4Ve=KA2×10 62+2×6Ve=KA2×20 得Ve=1升, KA2 =2.4升2/分 ∴ τ=30min时 V = KA2τ + Ve2 − Ve = 2.4 × 30 + 12 − 1 = 7.54升
=
12 30 + 6 +
20
=
0.21l
/ min
例: 某叶滤机恒压操作
τ(min)= 10 + 10 + 10
① V(l) = 4 + 2 + ?
② 过 滤 了 30min 后 , 用 VW=0.2V 总 的 洗 涤 液 量 洗 涤,ΔP洗=ΔP滤,μ洗液=μ滤液,则τW=? ③每次过滤洗涤后, 所需装卸时间τD为20min,
⎜⎛ ⎝
dV dτ
⎟⎞ ⎠W
= 0.2 × 7.54 = 10.7min 0.141
③ 生产能力
Q= V
=
7.54 = 0.124升 / 分
τ + τW + τ D 30 + 10.7 + 20
问题
• 恒速过滤,介质阻力不计,滤饼不可压缩,V 增加一倍, τ 不变,Δp增大至原来多少 倍?
• 恒压过滤,介质阻力不计,滤饼不可压缩,操 作压差增加一倍,所得滤液量不变,过滤时间 为原来的多少?
Δ℘ =℘1 −℘3 = Δ℘1 + Δ℘2为总压差 qe为过滤介质当量滤液量
u 表观速度
过滤基本方程
dq = Δ℘
参数归并法
dτ rμφ(q + qe )过滤常数
令K = 2Δ℘
dq dτ
=
K
2(q +
qe
)
dV dτ
=
KA 2
2(V + Ve )
q=V
rφμ
A
-----过滤基本方程
过滤常数K, qe是否真为常数,K是否与压差成正 比,得看条件
= Kτ 2
K 2
A 2τ
----恒速过滤方程
若过滤介质阻力可忽略不计(qe=0),则
V 2 = K A 2τ 2
或
q2 = K τ
2
2、恒压过滤 特点:K为常数
u=
dV Adτ
=
过滤推动力
过滤阻力 =
KA2
2(V +Ve )
K = 2Δ℘1−s r0φμ
∫ ∫ v
2 0 (V + Ve )dv =
4.4.3间歇过滤的滤液量与过滤时间的关系 1.恒速过滤
u = dq = K = 常数 dτ 2( q + qe )
K
=
2Δ℘ rφμ
Δ℘, K一直在变
若τ=0, q=0则
q = uτ
q终 =
K终
τ 终 2(q终 + qe )
恒速过滤特点:K不为常数,而u为常数
q=V A
整理得: 或
V q2
2
+
+ VV e qqe =
1500
τ q
=
1 K
q
+
2 K
qe
已测得 q和τ
τ 1000 q
500
可求qe 截距 2qe/K
0
0
0.025
0.05
q
思考
如何测压缩指数S?
斜率 1/K
可求K
0.075
如何测压缩指数S?
K = 2Δ℘ = 2Δ℘1− S
rφμ
r0φμ
K = 2Δ℘1−s r0φμ
不同的压差求出不同的K
log K = (1 − s) log Δ℘ + C
问题
叶滤机中如滤饼不可压缩,当过滤压差增加一倍时,过 滤速率是原来的 _2__ 倍。粘度增加一倍时,过滤速率是
原来的_1_/2 倍。 过滤速率基本方程
dq = K = Δ℘1−S dτ 2(q + qe ) r0φμ(q + qe )
s=0
操作压差: Δ℘与速率成正比
介质阻力: qe 滤饼因素: r0 ,φ , μ与速率成反比
或⎜⎛ dV ⎟⎞ = Δ℘W μ ⎜⎛ dV ⎟⎞ ⎝ dτ ⎠W Δ℘ μW ⎝ dτ ⎠
dV = KA2 dτ 2(V + Ve )
τW
=
VW
⎜⎝⎛
dV dτ
⎟⎞ ⎠W
=
Δ℘ Δ℘W
μW μ
2(V V2 +
+ Ve ) 2VVe
VWτ
当Ve=0时
τW
=
Δ℘ Δ℘W
μW μ
2VW τ V
例 某叶滤机恒压过滤操作, 过滤介质阻力可忽 略,过滤终了V=0.5m3,τ=1h,滤液粘度是水的四 倍。现用水洗涤,VW=0.05m3, 则τW= 。
K, qe的影响因素
①
K = 2Δ℘ rφμ
r = r0Δ℘s
压缩指数 s=0.2∼0.8(可压缩滤饼)
滤饼比阻r:
s=0(不可压缩滤饼)
不可压缩滤饼,s=0, r=r0=常数, K∝ΔP 可压缩滤饼, s ≠ 0 r=r0 ΔPS, K∝ΔP1-S
② qe与介质性质、悬浮液性质有关
若过滤介质阻力不计 → qe =0
τ KA2dτ
0
q=V A
积分得: V 2 + 2VVe = KA 2τ
或
q 2 + 2qqe = Kτ -----恒压过滤方程
q = Kτ + qe2 − qe
若过滤介质阻力可忽略不计(qe=0) ,则
V 2 = KA 2τ
或
q 2 = Kτ
3. 先恒速后恒压 先恒速再恒压操作,恒压段过滤方程?
u=
∫ dτ
τ = τ1
q1 = K 恒速终 τ 1 2( q1 + qe ) K 恒速终 = K 恒压
( q2 − q12 ) + 2( q − q1 )qe = K恒压 (τ −τ 1 ) q为总量
4. 过滤常数(k, qe)的测定 由小装置上测定的实验数据能否用于大装置? 考察影响因素
qe= f (过滤介质,悬浮液性质) 与A无关(而Ve∝A)
Δ℘w 为洗涤的总压差 μw 为洗涤液的粘度
洗涤液 △p
u 表观速度
② 洗涤时间τw
τw
=
Vw
⎜⎛ ⎝
dV dτ
⎟⎞ ⎠w
当Δ℘ = Δ℘w,
Vw(qw)为洗涤用量
μw = μ
⎜⎝⎛
dV dτ
⎟⎞ ⎠w
=
KA2 2(V + Ve )
=
dV dτ
τw
=
Vw
(dV dτ)w
=
2(V
+ Ve KA2
)Vw
问题
• 恒速过滤,介质阻力不计,滤饼不可压缩,V
增加一倍, τ 不变,Δp增大至原来多少
倍? V 2 = K A2τ 2
