20122017年高考文科数学真题汇编导数及应用老师版
20122017年高考文科数学真题汇编数列高考题老师版
A. 31B. 32C. 63D. 64 【答案】C9．（2013江西理）等比数列x,3x ＋3,6x ＋6，…的第四项等于( ) A ．－24 B ．0C ．12D ．24【答案】A10. (2013新标1文) 设首项为1，公比为的等比数列{}n a 的前n 项和为n S ，则（ ） （A ）21n n S a =- （B ）32n n S a =- （C ）43n n S a =- （D ）32n n S a =- 【答案】D11.（2015年新课标2文）设n S 是等差数列{}n a 的前n 项和,若1353a a a ++=,则5S =（ ） A ．5 B ．7 C ．9 D ．11 【答案】A12.（2015年新课标2文）已知等比数列{}n a 满足114a =,()35441a a a =-,则2a =（ ）A.2B.1 1C.2 1D.8【答案】C13、（2016年全国I 理）已知等差数列{}n a 前9项的和为27，10=8a ，则100=a（A ）100 （B ）99 （C ）98 （D ）97【答案】C14．（2014辽宁）设等差数列{}n a 的公差为d ，若数列1{2}na a 为递减数列，则（ ）A ．0d <B ．0d >C ．10a d <D ．10a d > 【答案】D15.（2015年新课标2理）等比数列｛a n ｝满足a 1=3，135a a a ++ =21，则357a a a ++= ( )（A ）21 （B ）42 （C ）63 （D ）84 【答案】B16．（2012大纲理）已知等差数列{}n a 的前n 项和为55,5,15n S a S ==，则数列11n n a a +⎧⎫⎨⎬⎩⎭的前100项和为A ．100101 B ．99101 C ．99100 D ．101100(-100 2所以61642128b-=⨯=.由12822n=+，得63n=.所以6b与数列{}n a的第63项相等.37、（2016年全国I卷）已知{}n a是公差为3的等差数列，数列{}n b满足12111==3n n n nb b a b b nb+++=1，，. （I）求{}n a的通项公式；（II）求{}n b的前n项和.解：（I）由已知，1221121,1,,3a b b b b b+===得1221121,1,,3a b b b b b+===得12a=，所以数列{}n a是首项为2，公差为3的等差数列，通项公式为31na n=-.（II）由（I）和11n n n na b b nb+++=，得13nnbb+=，因此{}n b是首项为1，公比为13的等比数列.记{}n b的前n项和为nS，则111()313.122313nn nS--==-⨯-38、（2016年全国III卷）已知各项都为正数的数列{}n a满足11a=，211(21)20n n n na a a a++---=.（I）求23,a a；（II）求{}n a的通项公式.39、（2016年全国II卷）等差数列{na}中，34574,6a a a a+=+=.（Ⅰ）求{na}的通项公式；解析：(Ⅰ)设数列{}n a的公差为d，由题意有11254,53a d a d-=-=，解得121,5a d==，所以{}n a的通项公式为235nna+=.40.（2015年福建文科）等差数列{}n a中，24a=，4715a a+=．（Ⅰ）求数列{}n a的通项公式；（Ⅱ）设22n anb n-=+，求12310b b b b+++⋅⋅⋅+的值．【答案】（Ⅰ）2na n=+；（Ⅱ）2101．【解析】试题分析：（Ⅰ）利用基本量法可求得1,a d，进而求{}n a的通项公式；（Ⅱ）求数列前n项和，首先考虑其通项公式，根据通项公式的不同特点，选择相应的求和方法，本题2nnb n=+，故可采取分组求和法求其前10项和．试题解析：（I）设等差数列{}n a的公差为d．由已知得()()11143615a da d a d+=⎧⎪⎨+++=⎪⎩，解得131ad=⎧⎨=⎩．所以()112na a n d n=+-=+．考点：1、等差数列通项公式；2、分组求和法．41、（2016年北京高考）已知{a n}是等差数列，{b n}是等比数列，且b2=3，b3=9，a1=b1，a14=b4.（Ⅰ）求{a n}的通项公式；（Ⅱ）设c n= a n+ b n，求数列{c n}的前n项和.解：（I）等比数列{}n b的公比32933bqb===，所以211bbq==，4327b b q==．设等差数列{}n a的公差为d．因为111a b==，14427a b==，所以11327d+=，即2d=．所以21na n=-（1n=，2，3，⋅⋅⋅）．（II）由（I）知，21na n=-，13nnb-=．因此1213nn n nc a b n-=+=-+．从而数列{}n c的前n项和()11321133nnS n-=++⋅⋅⋅+-+++⋅⋅⋅+()12113213nn n+--=+-学科网2312nn-=+．。
(2017-2019)高考文数真题分类汇编专题04 导数及其应用(解答题)(教师版)
专题04 导数及其应用（解答题）1．【2019年高考全国Ⅰ卷文数】已知函数f （）=2sin -cos -，f ′（）为f （）的导数．（1）证明：f ′（）在区间（0，π）存在唯一零点； （2）若∈[0，π]时，f （）≥a ，求a 的取值范围． 【答案】（1）见解析；（2）(],0a ∈-∞.【解析】（1）设()()g x f x '=，则()cos sin 1,()cos g x x x x g x x x '=+-=.当π(0,)2x ∈时，()0g x '>；当π,π2x ⎛⎫∈ ⎪⎝⎭时，()0g x '<，所以()g x 在π(0,)2单调递增，在π,π2⎛⎫⎪⎝⎭单调递减. 又π(0)0,0,(π)22g g g ⎛⎫=>=-⎪⎝⎭，故()g x 在(0,π)存在唯一零点. 所以()f x '在(0,π)存在唯一零点.（2）由题设知(π)π,(π)0f a f =…，可得a ≤0.由（1）知，()f x '在(0,π)只有一个零点，设为0x ，且当()00,x x ∈时，()0f x '>；当()0,πx x ∈时，()0f x '<，所以()f x 在()00,x 单调递增，在()0,πx 单调递减.又(0)0,(π)0f f ==，所以，当[0,π]x ∈时，()0f x …. 又当0,[0,π]a x ∈„时，a ≤0，故()f x ax …. 因此，a 的取值范围是(,0]-∞.【名师点睛】本题考查利用导数讨论函数零点个数、根据恒成立的不等式求解参数范围的问题.对于此类端点值恰为恒成立不等式取等的值的问题，通常采用构造函数的方式，将问题转变成函数最值与零之间的比较，进而通过导函数的正负确定所构造函数的单调性，从而得到最值.2．【2019年高考全国Ⅱ卷文数】已知函数()(1)ln 1f x x x x =---．证明：（1）()f x 存在唯一的极值点；（2）()=0f x 有且仅有两个实根，且两个实根互为倒数．【答案】（1）见解析；（2）见解析.【解析】（1）()f x 的定义域为（0，+）.11()ln 1ln x f x x x x x-'=+-=-. 因为ln y x =单调递增，1y x=单调递减，所以()f x '单调递增，又(1)10f '=-<，1ln 41(2)ln 2022f -'=-=>，故存在唯一0(1,2)x ∈，使得()00f x '=.又当0x x <时，()0f x '<，()f x 单调递减；当0x x >时，()0f x '>，()f x 单调递增. 因此，()f x 存在唯一的极值点.（2）由（1）知()0(1)2f x f <=-，又()22e e 30f =->，所以()0f x =在()0,x +∞内存在唯一根x α=.由01x α>>得011x α<<.又1111()1ln 10f f αααααα⎛⎫⎛⎫=---==⎪ ⎪⎝⎭⎝⎭，故1α是()0f x =在()00,x 的唯一根. 综上，()0f x =有且仅有两个实根，且两个实根互为倒数．【名师点睛】本题主要考查导数的应用，通常需要对函数求导，用导数的方法研究函数的单调性、极值，以及函数零点的问题，属于常考题型.3．【2019年高考天津文数】设函数()ln (1)e x f x x a x =--，其中a ∈R .（Ⅰ）若a ≤0，讨论()f x 的单调性； （Ⅱ）若10ea <<， （i ）证明()f x 恰有两个零点；（ii ）设0x 为()f x 的极值点，1x 为()f x 的零点，且10x x >，证明0132x x ->. 【答案】（Ⅰ）()f x 在(0,)+∞内单调递增.；（Ⅱ）（i ）见解析；（ii ）见解析. 【解析】（Ⅰ）解：由已知，()f x 的定义域为(0,)+∞，且211e ()e (1)e x x xf ax x a a x x x-⎡⎤=-+-=⎣'⎦. 因此当a ≤0时，21e 0x ax ->，从而()0f x '>，所以()f x 在(0,)+∞内单调递增.（Ⅱ）证明：（i ）由（Ⅰ）知21e ()xax f x x-'=.令2()1e x g x ax =-，由10e a <<， 可知()g x 在(0,)+∞内单调递减，又(1)1e 0g a =->，且221111ln 1ln 1ln 0g a a a a a ⎛⎫⎛⎫⎛⎫=-=-< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 故()0g x =在(0,)+∞内有唯一解，从而()0f x '=在(0,)+∞内有唯一解，不妨设为0x ，则011ln x a<<.当()00,x x ∈时，()0()()0g x g x f x x x'=>=，所以()f x 在()00,x 内单调递增；当()0,x x ∈+∞时，()0()()0g x g x f x x x'=<=，所以()f x 在()0,x +∞内单调递减，因此0x 是()f x 的唯一极值点.令()ln 1h x x x =-+，则当1x >时，1()10h'x x=-<，故()h x 在(1,)+∞内单调递减，从而当1x >时，()(1)0h x h <=，所以ln 1x x <-.从而ln 1111111ln ln ln ln 1e ln ln ln 1ln 0a f a h a a a a a a ⎛⎫⎛⎫⎛⎫=--=-+=< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，又因为()0(1)0f x f >=，所以()f x 在0(,)x +∞内有唯一零点.又()f x 在()00,x 内有唯一零点1，从而，()f x 在(0,)+∞内恰有两个零点.（ii ）由题意，()()010,0,f x f x '=⎧⎪⎨=⎪⎩即()012011e 1,ln e ,1x x ax x a x ⎧=⎪⎨=-⎪⎩从而1011201ln e x x x x x --=，即102011ln e 1x x x x x -=-.因为当1x >时，ln 1x x <-，又101x x >>，故()102012011e 1x x x x x x --<=-，两边取对数，得1020ln e ln x x x -<，于是()10002ln 21x x x x -<<-，整理得0132x x ->.【名师点睛】本小题主要考查导数的运算、不等式证明、运用导数研究函数的性质等基础知识和方法.考查函数思想、化归与转化思想.考查综合分析问题和解决问题的能力. 4．【2019年高考全国Ⅲ卷文数】已知函数32()22f x x ax =-+．（1）讨论()f x 的单调性；（2）当0<a <3时，记()f x 在区间[0，1]的最大值为M ，最小值为m ，求M m -的取值范围． 【答案】（1）见详解；（2）8[,2)27. 【解析】（1）2()622(3)f x x ax x x a '=-=-． 令()0f x '=，得=0或3ax =． 若a >0，则当(,0),3a x ⎛⎫∈-∞+∞⎪⎝⎭U 时，()0f x '>；当0,3a x ⎛⎫∈ ⎪⎝⎭时，()0f x '<．故()f x 在(,0),,3a ⎛⎫-∞+∞ ⎪⎝⎭单调递增，在0,3a ⎛⎫⎪⎝⎭单调递减；若a =0，()f x 在(,)-∞+∞单调递增；若a <0，则当,(0,)3a x ⎛⎫∈-∞+∞ ⎪⎝⎭U 时，()0f x '>；当,03a x ⎛⎫∈ ⎪⎝⎭时，()0f x '<．故()f x 在,,(0,)3a ⎛⎫-∞+∞ ⎪⎝⎭单调递增，在,03a ⎛⎫⎪⎝⎭单调递减．（2）当03a <<时，由（1）知，()f x 在0,3a ⎛⎫ ⎪⎝⎭单调递减，在,13a ⎛⎫ ⎪⎝⎭单调递增，所以()f x 在[0,1]的最小值为32327a a f ⎛⎫=-+ ⎪⎝⎭，最大值为(0)=2f 或(1)=4f a -.于是 3227a m =-+，4,02,2,2 3.a a M a -<<⎧=⎨≤<⎩所以332,02,27,2 3.27a a a M m a a ⎧-+<<⎪⎪-=⎨⎪≤<⎪⎩当02a <<时，可知3227a a -+单调递减，所以M m -的取值范围是8,227⎛⎫⎪⎝⎭． 当23a ≤<时，327a 单调递增，所以M m -的取值范围是8[,1)27．综上，M m -的取值范围是8[,2)27． 【名师点睛】这是一道常规的导数题目，难度比往年降低了不少.考查函数的单调性，最大值、最小值的计算.5．【2019年高考北京文数】已知函数321()4f x x x x =-+． （Ⅰ）求曲线()y f x =的斜率为1的切线方程； （Ⅱ）当[2,4]x ∈-时，求证：6()x f x x -≤≤；（Ⅲ）设()|()()|()F x f x x a a =-+∈R ，记()F x 在区间[2,4]-上的最大值为M （a ），当M （a ）最小时，求a 的值．【答案】（Ⅰ）y x =与6427y x =-；（Ⅱ）见解析；（Ⅲ）3a =-. 【解析】（Ⅰ）由321()4f x x x x =-+得23()214f x x x '=-+．令()1f x '=，即232114x x -+=，得0x =或83x =．又(0)0f =，88()327f =，所以曲线()y f x =的斜率为1的切线方程是y x =与88273y x -=-，即y x =与6427y x =-．（Ⅱ）令()(),[2,4]g x f x x x =-∈-．由321()4g x x x =-得23()24g'x x x =-． 令()0g'x =得0x =或83x =．(),()g'x g x 的情况如下：所以()g x 的最小值为6-，最大值为0． 故6()0g x -≤≤，即6()x f x x -≤≤． （Ⅲ）由（Ⅱ）知，当3a <-时，()(0)|(0)|3M F g a a a ≥=-=->； 当3a >-时，()(2)|(2)|63M F a g a a ≥-=--=+>； 当3a =-时，()3M a =． 综上，当()M a 最小时，3a =-．【名师点睛】本题主要考查利用导函数研究函数的切线方程，利用导函数证明不等式的方法，分类讨论的数学思想等知识，意在考查学生的转化能力和计算求解能力.6．【2019年高考浙江】已知实数0a ≠，设函数()=ln 0.f x a x x +>（1）当34a =-时，求函数()f x 的单调区间；（2）对任意21[,)e x ∈+∞均有()2f x a ≤ 求a 的取值范围． 注：e=2.71828…为自然对数的底数．【答案】（1）()f x 的单调递增区间是()3,+∞,单调递减区间是()0,3；（2）0,4⎛ ⎝⎦.【解析】（1）当34a =-时，3()ln 04f x x x =->．3()4f 'x x =-=， 所以，函数()f x 的单调递减区间为（0，3），单调递增区间为（3，+）．（2）由1(1)2f a≤，得04a <≤．当0a <≤()f x ≤2ln 0x -≥．令1t a=，则t ≥．设()22ln ,g t t x t =≥则2()2ln g t t x=-．（i ）当1,7x ⎡⎫∈+∞⎪⎢⎣⎭≤()2ln g t g x ≥=．记1()ln ,7p x x x =≥，则1()p'x x =-==.故所以，()(1)0p x p ≥=．因此，()2()0g t g p x ≥=≥．（ii ）当211,e 7x ⎡⎫∈⎪⎢⎣⎭时，()g t g =…令211()(1),,e 7q x x x x ⎡⎤=++∈⎢⎥⎣⎦ ， 则()10q'x=+>， 故()q x 在211,e 7⎡⎤⎢⎥⎣⎦上单调递增，所以1()7q x q ⎛⎫⎪⎝⎭„．由（i ）得，11(1)07777q p p ⎛⎫⎛⎫=-<-= ⎪ ⎪⎝⎭⎝⎭． 所以，()<0q x ．因此()0g t g =>…．由（i ）（ii ）知对任意21,e x ⎡⎫∈+∞⎪⎢⎣⎭，),()0t g t ∈+∞…，即对任意21,e x ⎡⎫∈+∞⎪⎢⎣⎭，均有()2f x a „．综上所述，所求a 的取值范围是4⎛ ⎝⎦．【名师点睛】导数是研究函数的单调性、极值(最值)最有效的工具，而函数是高中数学中重要的知识点，对导数的应用的考查主要从以下几个角度进行：（1）考查导数的几何意义，往往与解析几何、微积分相联系．（2）利用导数求函数的单调区间，判断单调性；已知单调性，求参数．（3）利用导数求函数的最值(极值)，解决生活中的优化问题．（4）考查数形结合思想的应用．7．【2019年高考江苏】设函数()()()(),,,f x x a x b x c a b c =---∈R 、()f 'x 为f （）的导函数． （1）若a =b =c ，f （4）=8，求a 的值；（2）若a ≠b ，b =c ，且f （）和()f 'x 的零点均在集合{3,1,3}-中，求f （）的极小值；（3）若0,01,1a b c =<=„，且f （）的极大值为M ，求证M ≤427． 【答案】（1）2a =；（2）见解析；（3）见解析.【解析】（1）因为a b c ==，所以3()()()()()f x x a x b x c x a =---=-． 因为(4)8f =，所以3(4)8a -=， 解得2a =． （2）因为b c =，所以2322()()()(2)(2)f x x a x b x a b x b a b x ab =--=-+++-， 从而2()3()3a b f 'x x b x +⎛⎫=--⎪⎝⎭．令()0f 'x =，得x b =或23a bx +=．因为2,,3a ba b +都在集合{3,1,3}-中，且a b ≠， 所以21,3,33a b a b +===-．此时2()(3)(3)f x x x =-+，()3(3)(1)f 'x x x =+-． 令()0f 'x =，得3x =-或1x =．列表如下：所以()f x 的极小值为2(1)(13)(13)32f =-+=-．（3）因为0,1a c ==，所以32()()(1)(1)f x x x b x x b x bx =--=-++，2()32(1)f 'x x b x b =-++．因为01b <≤，所以224(1)12(21)30b b b ∆=+-=-+>， 则()f 'x 有2个不同的零点，设为()1212,x x x x <．由()0f 'x =，得121133b b x x ++==．列表如下：所以()f x 的极大值()1M f x =． 解法一：()321111(1)M f x x b x bx ==-++()221111211(1)[32(1)]3999b b x b b b x b x b x -+++⎛⎫=-++--+ ⎪⎝⎭()2321(1)(1)227927b b b b b --+++=++23(1)2(1)(1)2272727b b b b +-+=-+(1)24272727b b +≤+≤．因此427M ≤． 解法二：因为01b <≤，所以1(0,1)x ∈．当(0,1)x ∈时，2()()(1)(1)f x x x b x x x =--≤-． 令2()(1),(0,1)g x x x x =-∈，则1()3(1)3g'x x x ⎛⎫=-- ⎪⎝⎭． 令()0g'x =，得13x =．列表如下：所以当13x =时，()g x 取得极大值，且是最大值，故max 14()327g x g ⎛⎫== ⎪⎝⎭．所以当(0,1)x ∈时，4()()27f x g x ≤≤，因此427M ≤． 【名师点睛】本题主要考查利用导数研究函数的性质，考查综合运用数学思想方法分析与解决问题以及逻辑推理能力．8．【2018年高考全国Ⅲ卷文数】已知函数21()exax x f x +-=． （1）求曲线()y f x =在点(0,1)-处的切线方程； （2）证明：当1a ≥时，()e 0f x +≥． 【答案】（1）210x y --=；（2）见解析.【解析】（1）2(21)2()exax a x f x -+-+'=，(0)2f '=． 因此曲线()y f x =在点(0,1)-处的切线方程是210x y --=． （2）当1a ≥时，21()e (1e )e x x f x x x +-+≥+-+．令21()1ex g x x x +=+-+，则1()21ex g x x +'=++．当1x <-时，()0g x '<，()g x 单调递减；当1x >-时，()0g x '>，()g x 单调递增； 所以()g x (1)=0g ≥-．因此()e 0f x +≥．【名师点睛】本题考查函数与导数的综合应用，第一问由导数的几何意义可求出切线方程，第二问当1a ≥时，21()e (1e)e x x f x x x +-+≥+-+，令21()1e x g x x x +=+-+，求出()g x 的最小值即可证明.9．【2018年高考全国Ⅰ卷文数】已知函数()e ln 1xf x a x =--． （1）设2x =是()f x 的极值点，求a ，并求()f x 的单调区间；（2）证明：当1ea ≥时，()0f x ≥． 【答案】（1）在（0，2）单调递减，在（2，+∞）单调递增；（2）见解析.【解析】（1）f （）的定义域为(0)+∞，，f ′（）=a e –1x． 由题设知，f ′（2）=0，所以a =212e． 从而f （）=21e ln 12e x x --，f ′（）=211e 2e x x-． 当0<<2时，f ′（）<0；当>2时，f ′（）>0．所以f （）在（0，2）单调递减，在（2，+∞）单调递增．（2）当a ≥1e 时，f （）≥e ln 1exx --．设g （）=e ln 1e x x --，则e 1()e x g x x'=-．当0<<1时，g ′（）<0；当>1时，g ′（）>0．所以=1是g （）的最小值点． 故当>0时，g （）≥g （1）=0． 因此，当1ea ≥时，()0f x ≥．【名师点睛】该题考查的是有关导数的应用问题，涉及的知识点有导数与极值、导数与最值、导数与函数的单调性的关系以及证明不等式问题，在解题的过程中，首先要确定函数的定义域，之后根据导数与极值的关系求得参数值，之后利用极值的特点，确定出函数的单调区间，第二问在求解的时候构造新函数，应用不等式的传递性证得结果. 10．【2018年高考全国Ⅱ卷文数】已知函数()()32113f x x a x x =-++． （1）若3a =，求()f x 的单调区间；（2）证明：()f x 只有一个零点．【答案】（1）在（–∞，3-3++∞）单调递增，在（3-，3+减；（2）见解析.【解析】（1）当a =3时，f （）=3213333x x x ---，f ′（）=263x x --．令f ′（）=0解得=3-=3+当∈（–∞，3-3++∞）时，f ′（）>0；当∈（3-3+ f ′（）<0．故f （）在（–∞，3-3++∞）单调递增，在（3-，3+（2）由于210x x ++>，所以()0f x =等价于32301x a x x -=++．设()g x =3231x a x x -++，则g ′（）=2222(23)(1)x x x x x ++++≥0，仅当=0时g ′（）=0， 所以g （）在（–∞，+∞）单调递增．故g （）至多有一个零点，从而f （）至多有一个零点． 又f （3a –1）=22111626()0366a a a -+-=---<， f （3a +1）=103>，故f （）有一个零点． 综上，f （）只有一个零点．【名师点睛】（1）用导数求函数单调区间的步骤如下：①确定函数的定义域；②求导数；③由（或）解出相应的的取值范围，当时，在相应区间上是增函数；当时，在相应区间上是减增函数.（2）本题第二问重在考查零点存在性问题，解题的关键在于将问题转化为求证函数有唯一零点，可先证明其单调，再结合零点存在性定理进行论证.11．【2018年高考北京文数】设函数2()[(31)32]e x f x ax a x a =-+++.（Ⅰ）若曲线()y f x =在点(2,(2))f 处的切线斜率为0，求a ； （Ⅰ）若()f x 在1x =处取得极小值，求a 的取值范围. 【答案】（Ⅰ）12a =；（Ⅱ）(1,)+∞. 【解析】（Ⅰ）因为2()[(31)32]e xf x ax a x a =-+++， 所以2()[(1)1]e xf x ax a x '=-++.2(2)(21)e f a '=-，由题设知(2)0f '=，即2(21)e 0a -=，解得12a =. （Ⅱ）方法一：由（Ⅰ）得2()[(1)1]e (1)(1)e xxf x ax a x ax x '=-++=--. 若a >1，则当1(,1)x a∈时，()0f x '<； 当(1,)x ∈+∞时，()0f x '>. 所以()f x 在=1处取得极小值.若1a ≤，则当(0,1)x ∈时，110ax x -≤-<， 所以()0f x '>.所以1不是()f x 的极小值点. 综上可知，a 的取值范围是(1,)+∞. 方法二：()(1)(1)e xf x ax x '=--. （1）当a =0时，令()0f x '=得=1.(),()f x f x '随的变化情况如下表：∴()f x 在=1处取得极大值，不合题意. （2）当a >0时，令()0f x '=得121,1ax x ==. ①当12x x =，即a =1时，2()(1)e 0xf x x '=-≥， ∴()f x 在R 上单调递增， ∴()f x 无极值，不合题意.②当12x x >，即0<a <1时，(),()f x f x '随的变化情况如下表：∴()f x 在=1处取得极大值，不合题意.③当12x x <，即a >1时，(),()f x f x '随的变化情况如下表：∴()f x 在=1处取得极小值，即a >1满足题意. （3）当a <0时，令()0f x '=得121,1ax x ==. (),()f x f x '随的变化情况如下表：∴()f x 在=1处取得极大值，不合题意. 综上所述，a 的取值范围为(1,)+∞.【名师点睛】导数类问题是高考数学中的必考题，也是压轴题，主要考查的形式有以下四个：①考查导数的几何意义，涉及求曲线切线方程的问题；②利用导数证明函数的单调性或求单调区间问题；③利用导数求函数的极值、最值问题；④关于不等式的恒成立问题.解题时需要注意以下两个方面：①在求切线方程问题时，注意区别在某一点和过某一点解题步骤的不同；②在研究单调性及极值、最值问题时常会涉及分类讨论的思想，要做到不重不漏；③不等式的恒成立问题属于高考中的难点，要注意问题转换的等价性.12．【2018年高考天津文数】设函数123()=()()()f x x t x t x t ---，其中123,,t t t ∈R ,且123,,t t t 是公差为d 的等差数列．（I ）若20,1,t d ==求曲线()y f x =在点(0,(0))f 处的切线方程； （II ）若3d =，求()f x 的极值；（III ）若曲线()y f x =与直线2()y x t =---d 的取值范围．【答案】（I ）+y =0；（II ）函数f ()的极大值为f ()的极小值为−；（III ）d 的取值范围为(,)-∞+∞U .【解析】（Ⅰ）解：由已知，可得f ()=(−1)(+1)=3−，故()f x '=32−1， 因此f (0)=0，(0)f '=−1，又因为曲线y =f ()在点(0，f (0))处的切线方程为y −f (0)=(0)f '(−0)， 故所求切线方程为+y =0． （Ⅱ）解：由已知可得f ()=(−t 2+3)(−t 2)(−t 2−3)=(−t 2)3−9(−t 2)=3−3t 22+(3t 22−9)−t 23+9t 2．故()f x '=32−6t 2+3t 22−9．令()f x '=0，解得=t 2，或=t 2 当变化时，()f x '，f ()的变化如下表：所以函数f ()的极大值为f (t 2)=(3−9×(；函数f ()的极小值为f (t 2)3−9×−（Ⅲ）解：曲线y =f ()与直线y =−(−t 2)−有三个互异的公共点等价于关于的方程(−t 2+d )(−t 2)(−t 2−d )+(−t 2有三个互异的实数解，令u =−t 2，可得u 3+(1−d 2)u ．设函数g ()=3+(1−d 2y =f ()与直线y =−(−t 2)−y =g ()有三个零点．()g'x =33+(1−d 2)．当d 2≤1时，()g'x ≥0，这时()g x 在R 上单调递增，不合题意．当d 2>1时，()g'x =0，解得1=2．易得，g ()在(−∞，1)上单调递增，在[1，2]上单调递减，在(2，+∞)上单调递增．g ()的极大值g (1)=g (3221)9d -+．g ()的极小值g (2)=g )=+ 若g (2)≥0，由g ()的单调性可知函数y =g ()至多有两个零点，不合题意．若2()0,g x <即322(1)27d ->，也就是||d >，此时2||d x >，(||)||0,g d d =+>且312||,(2||)6||2||0d x g d d d -<-=--+<-<，从而由()g x 的单调性，可知函数()y g x =在区间1122(2||,),(,),(,||)d x x x x d -内各有一个零点，符合题意．所以，d 的取值范围是(,)-∞+∞U ．【名师点睛】本小题主要考查导数的运算、导数的几何意义、运用导数研究函数的性质等基础知识和方法，考查函数思想和分类讨论思想，考查综合分析问题和解决问题的能力. 13．【2018年高考浙江】已知函数f−ln ．（Ⅰ）若f ()在=1，2(1≠2)处导数相等，证明：f (1)+f (2)>8−8ln2；（Ⅱ）若a ≤3−4ln2，证明：对于任意>0，直线y =+a 与曲线y =f ()有唯一公共点． 【答案】（Ⅰ）见解析；（Ⅱ）见解析. 【解析】（Ⅰ）函数f（）的导函数1()f x x'=， 由12()()f x f x ''=1211x x =， 因为12x x ≠12=．=≥ 因为12x x ≠，所以12256x x >．由题意得121212()()ln ln ln()f x f x x x x x +==．设()ln g x x =，则1()4)4g x x'=， 所以所以g （）在[256，+∞）上单调递增， 故12()(256)88ln 2g x x g >=-， 即12()()88ln 2f x f x +>-． （Ⅱ）令m =()e a k -+，n =21()1a k++，则f （m ）–m –a >|a |+––a ≥0， f （n ）–n –a<)a n k n-≤)n k <0， 所以，存在0∈（m ，n ）使f （0）=0+a ，所以，对于任意的a ∈R 及∈（0，+∞），直线y =+a 与曲线y =f （）有公共点． 由f （）=+a得k =设()h x =则22ln )1)((12x ag x x x a x h '=-+--+=，其中(n )l g x x -=． 由（Ⅰ）可知g （）≥g （16），又a ≤3–4ln2， 故–g （）–1+a ≤–g （16）–1+a =–3+4ln2+a ≤0，所以h ′（）≤0，即函数h （）在（0，+∞）上单调递减，因此方程f （）––a =0至多1个实根． 综上，当a ≤3–4ln2时，对于任意>0，直线y =+a 与曲线y =f （）有唯一公共点．【名师点睛】本题主要考查函数的单调性，导数的运算及其应用，同时考查逻辑思维能力和综合应用能力.14．【2018年高考江苏】某农场有一块农田，如图所示，它的边界由圆O 的一段圆弧MPN （P 为此圆弧的中点）和线段MN 构成．已知圆O 的半径为40米，点P 到MN 的距离为50米．现规划在此农田上修建两个温室大棚，大棚Ⅰ内的地块形状为矩形ABCD ，大棚Ⅱ内的地块形状为CDP △，要求,A B 均在线段MN 上，,C D 均在圆弧上．设OC 与MN 所成的角为θ．（1）用θ分别表示矩形ABCD 和CDP △的面积，并确定sin θ的取值范围；（2）若大棚Ⅰ内种植甲种蔬菜，大棚Ⅱ内种植乙种蔬菜，且甲、乙两种蔬菜的单位面积年产值之比为4:3．求当θ为何值时，能使甲、乙两种蔬菜的年总产值最大．【答案】（1）矩形ABCD的面积为800（4sinθcosθ+cosθ）平方米，△CDP的面积为1600（cosθ–sinθcosθ）平方米，sinθ的取值范围是[14，1]；（2）当θ=π6时，能使甲、乙两种蔬菜的年总产值最大．【解析】（1）连结PO并延长交MN于H，则PH⊥MN，所以OH=10．过O作OE⊥BC于E，则OE∥MN，所以∠COE=θ，故OE=40cosθ，EC=40sinθ，则矩形ABCD的面积为2×40cosθ（40sinθ+10）=800（4sinθcosθ+cosθ），△CDP的面积为12×2×40cosθ（40–40sinθ）=1600（cosθ–sinθcosθ）．过N作GN⊥MN，分别交圆弧和OE的延长线于G和，则G=N=10．令∠GO=θ0，则sinθ0=14，θ0∈（0，π6）．当θ∈[θ0，π2]时，才能作出满足条件的矩形ABCD，所以sinθ的取值范围是[14，1]．答：矩形ABCD的面积为800（4sinθcosθ+cosθ）平方米，△CDP的面积为1600（cosθ–sinθcosθ）平方米，sinθ的取值范围是[14，1]．（2）因为甲、乙两种蔬菜的单位面积年产值之比为4∶3，设甲的单位面积的年产值为4，乙的单位面积的年产值为3（>0），则年总产值为4×800（4sinθcosθ+cosθ）+3×1600（cosθ–sinθcosθ）=8000（sinθcosθ+cosθ），θ∈[θ0，π2 ]．设f （θ）=sin θcos θ+cos θ，θ∈[θ0，π2]， 则222()cos sin sin (2sin sin 1)(2sin 1)(sin 1)f θθθθθθθθ'=--=-+-=--+． 令()=0f θ'，得θ=π6， 当θ∈（θ0，π6）时，()0f θ'>，所以f （θ）为增函数； 当θ∈（π6，π2）时，()0f θ'<，所以f （θ）为减函数， 因此，当θ=π6时，f （θ）取到最大值． 答：当θ=π6时，能使甲、乙两种蔬菜的年总产值最大． 【名师点睛】本小题主要考查三角函数的应用、用导数求最值等基础知识，考查直观想象和数学建模及运用数学知识分析和解决实际问题的能力.15．【2018年高考江苏】记(),()f x g x ''分别为函数(),()f x g x 的导函数．若存在0x ∈R ，满足00()()f xg x =且00()()f x g x ''=，则称0x 为函数()f x 与()g x 的一个“S 点”． （1）证明：函数()f x x =与2()22g x x x =+-不存在“S 点”； （2）若函数2()1f x ax =-与()ln g x x =存在“S 点”，求实数a 的值；（3）已知函数2()f x x a =-+，e ()xb g x x=．对任意0a >，判断是否存在0b >，使函数()f x 与()g x 在区间(0,)+∞内存在“S 点”，并说明理由． 【答案】（1）见解析；（2）e2；（3）见解析. 【解析】（1）函数f （）=，g （）=2+2-2，则f ′（）=1，g ′（）=2+2． 由f （）=g （）且f ′（）= g ′（），得222122x x x x ⎧=+-⎨=+⎩，此方程组无解， 因此，f （）与g （）不存在“S ”点．（2）函数21f x ax =-（），()ln g x x =， 则12f x ax g x x'='=（），（）． 设0为f （）与g （）的“S ”点，由f （0）=g （0）且f ′（0）=g ′（0），得200001ln 12ax x ax x ⎧-=⎪⎨=⎪⎩，即200201ln 21ax x ax ⎧-=⎪⎨=⎪⎩，（*） 得01ln 2x =-，即120e x -=，则1221e 22(e )a -==． 当e 2a =时，120e x -=满足方程组（*），即0x 为f （）与g （）的“S ”点．因此，a 的值为e 2． （3）对任意a >0，设32()3h x x x ax a =--+．因为(0)0(1)1320h a h a a =>=--+=-<，，且h （）的图象是不间断的，所以存在0x ∈（0，1），使得0()0h x =．令03002e (1)x x b x =-，则b >0．函数2e ()()xb f x x a g x x=-+=，，则2e (1)()2()x b x f x x g x x-'=-=′，． 由f （）=g （）且f ′（）=g ′（），得22e e (1)2xx b x a x b x x x ⎧-+=⎪⎪⎨-⎪-=⎪⎩，即00320030202e e (1)2e (1)2e (1)x x xx x x a x x x x x x x ⎧-+=⋅⎪-⎪⎨-⎪-=⋅⎪-⎩，（**） 此时，0x 满足方程组（**），即0x 是函数f （）与g （）在区间（0，1）内的一个“S 点”． 因此，对任意a >0，存在b >0，使函数f （）与g （）在区间（0，+∞）内存在“S 点”．【名师点睛】本小题主要考查利用导数研究初等函数的性质，考查综合运用数学思想方法分析与解决问题以及逻辑推理能力.16．【2017年高考全国Ⅰ卷文数】已知函数()f x =e(e−a )−a 2．（1）讨论()f x 的单调性；（2）若()0f x ≥，求a 的取值范围．【答案】（1）当0a =时，)(x f 在(,)-∞+∞单调递增；当0a >时，()f x 在(,ln )a -∞单调递减，在(ln ,)a +∞单调递增；当0a <时，()f x 在(,ln())2a -∞-单调递减，在(ln(),)2a-+∞单调递增；（2）34[2e ,1]-．【解析】（1）函数()f x 的定义域为(,)-∞+∞，22()2e e (2e )(e )xx x x f x a a a a '=--=+-，①若0a =，则2()e xf x =，在(,)-∞+∞单调递增． ②若0a >，则由()0f x '=得ln x a =．当(,ln )x a ∈-∞时，()0f x '<；当(ln ,)x a ∈+∞时，()0f x '>，故()f x 在(,ln )a -∞单调递减，在(ln ,)a +∞单调递增．③若0a <，则由()0f x '=得ln()2a x =-．当(,ln())2a x ∈-∞-时，()0f x '<；当(ln(),)2a x ∈-+∞时，()0f x '>，故()f x 在(,ln())2a -∞-单调递减，在(ln(),)2a-+∞单调递增．（2）①若0a =，则2()e xf x =，所以()0f x ≥．②若0a >，则由（1）得，当ln x a =时，()f x 取得最小值，最小值为2(ln )ln f a a a =-．从而当且仅当2ln 0a a -≥，即1a ≤时，()0f x ≥．③若0a <，则由（1）得，当ln()2a x =-时，()f x 取得最小值，最小值为23(ln())[ln()]242a a f a -=--．从而当且仅当23[ln()]042aa --≥，即342e a ≥-时()0f x ≥．综上，a 的取值范围为34[2e ,1]-．【名师点睛】本题主要考查导数两大方面的应用：（1）函数单调性的讨论：运用导数知识讨论函数单调性时，首先考虑函数的定义域，再求出()f x '，由()f x '的正负，得出函数()f x 的单调区间；（2）函数的最值（极值）的求法：由确认的单调区间，结合极值点的定义及自变量的取值范围，得出函数()f x 的极值或最值．17．【2017年高考全国Ⅱ卷文数】设函数2()(1)e x f x x =-.（1）讨论()f x 的单调性；（2）当0x ≥时，()1f x ax ≤+，求a 的取值范围.【答案】（1）在(,1-∞--和(1)-++∞单调递减，在(11--+单调递增；（2）[1,)+∞. 【解析】（1）2()(12)e xf x x x '=--.令()0f x '=得1x x =--=-当(,1x ∈-∞--时，()0f x '<；当(11x ∈---时，()0f x '>；当(1)x ∈-+∞时，()0f x '<.所以()f x 在(,1-∞-和(1)-++∞单调递减，在(11---+单调递增.（2）()(1+)(1)e x f x x x =-.当a ≥1时，设函数h ()=（1−）e ，h′()= −e ＜0（＞0），因此h ()在[0，+∞)单调递减，而h (0)=1， 故h ()≤1，所以f ()=（+1）h ()≤+1≤a +1.当0＜a ＜1时，设函数g （）=e−−1，g ′（）=e−1＞0（＞0），所以g （）在[0，+∞)单调递增，而g (0)=0，故e≥+1.当0＜＜1时，2()(1)(1)f x x x >-+，22(1)(1)1(1)x x ax x a x x -+--=---，取0x =，则2000000(0,1),(1)(1)10,()1x x x ax f x ax ∈-+--=>+故.当0a ≤时，取0x =则0(0,1),x ∈20000()(1)(1)11f x x x ax >-+=>+. 综上，a 的取值范围是[1，+∞）.【名师点睛】利用导数研究不等式恒成立或存在型问题，首先要构造函数，利用导数研究函数的单调性，求出最值，进而得出相应的含参不等式，从而求出参数的取值范围；也可分离变量，构造函数，直接把问题转化为函数的最值问题.18．【2017年高考全国Ⅲ卷文数】已知函数()2(1)ln 2x ax a x f x =+++．（1）讨论()f x 的单调性； （2）当a ﹤0时，证明3()24f x a≤--．【答案】（1）当0≥a 时，)(x f 在),0(+∞单调递增；当0<a 时，)(x f 在)21,0(a-单调递增，在),21(+∞-a单调递减；（2）详见解析 【解析】（1）()f x 的定义域为（0，+∞），()()1211()221x ax f x ax a x x++'=+++=. 若0a ≥，则当(0)x ∈+∞，时，()0f x '>，故()f x 在（0，+∞）单调递增. 若0a <，则当1(0,)2x a ∈-时，()0f x '>；当1()2x a ∈-+∞，时，()0f x '<.故()f x 在1(0,)2a-单调递增，在1()2a-+∞，单调递减. （2）由（1）知，当0a <时，()f x 在12x a=-取得最大值，最大值为 111()ln()1224f a a a-=---. 所以3()24f x a ≤--等价于113ln()12244a a a ---≤--，即11ln()1022a a-++≤. 设()ln 1g x x x =-+，则1()1g x x '=-.当(0,1)x ∈时，()0g x '>；当∈（1，+∞）时，()0g x '<.所以()g x 在（0,1）单调递增，在（1，+∞）单调递减.故当=1时()g x 取得最大值，最大值为g （1）=0.所以当＞0时，()0g x ≤.从而当a ＜0时，11ln()1022a a -++≤，即3()24f x a≤--. 【名师点睛】利用导数证明不等式的常见类型及解题策略：（1）构造差函数()()()h x f x g x =-.根据差函数导函数符号，确定差函数单调性，利用单调性得不等量关系，进而证明不等式.（2）根据条件，寻找目标函数.一般思路为利用条件将求和问题转化为对应项之间大小关系，或利用放缩、等量代换将多元函数转化为一元函数.19．【2017年高考浙江】已知函数f ()=（e x -（12x ≥）． （1）求f ()的导函数；（2）求f ()在区间1[+)2∞，上的取值范围．【答案】（1）1())2f x x '=>；（2）121[0,e ]2-．【解析】（1）因为(1x '-=-，(e )e x x'--=-，所以()(1(x xf x x --'=--1)2x x -=>．（2）由()0f x '==，解得1x =或52x =．因为又21()1)e 02x f x -=≥， 所以f （）在区间1[,)2+∞上的取值范围是121[0,e ]2-．【名师点睛】本题主要考查导数两大方面的应用：（一）函数单调性的讨论：运用导数知识讨论函数单调性时，首先考虑函数的定义域，再求出()f'x ，由()f'x 的正负，得出函数()f x 的单调区间；（二）函数的最值（极值）的求法：由单调区间，结合极值点的定义及自变量的取值范围，得出函数()f x 的极值或最值．20．【2017年高考北京文数】已知函数()e cos x f x x x =-．（Ⅰ）求曲线()y f x =在点(0,(0))f 处的切线方程； （Ⅱ）求函数()f x 在区间π[0,]2上的最大值和最小值． 【答案】（Ⅰ）1y =；（Ⅱ）最大值为1；最小值为π2-. 【解析】（Ⅰ）因为()e cos x f x x x =-，所以()e (cos sin )1,(0)0xf x x x f ''=--=.又因为(0)1f =，所以曲线()y f x =在点(0,(0))f 处的切线方程为1y =.（Ⅰ）设()e (cos sin )1xh x x x =--，则()e (cos sin sin cos )2e sin xxh x x x x x x '=---=-.当π(0,)2x ∈时，()0h x '<， 所以()h x 在区间π[0,]2上单调递减.所以对任意π(0,]2x ∈有()(0)0h x h <=，即()0f x '<. 所以函数()f x 在区间π[0,]2上单调递减.因此()f x 在区间π[0,]2上的最大值为(0)1f =，最小值为ππ()22f =-. 【名师点睛】这道导数题并不难，比一般意义上的压轴题要简单很多，第二问比较有特点的是需要两次求导数，因为通过()f x '不能直接判断函数的单调性，所以需要再求一次导数，设()()h x f x '=，再求()h x '，一般这时就可求得函数()h x '的零点，或是()0h x '>(()0h x '<)恒成立，这样就能知道函数()h x 的单调性，再根据单调性求其最值，从而判断()y f x =的单调性，最后求得结果. 21．【2017年高考天津文数】设,a b ∈R ，||1a ≤．已知函数32()63(4)f x x x a a x b =---+，()e ()x g x f x =．（Ⅰ）求()f x 的单调区间；（Ⅱ）已知函数()y g x =和e x y =的图象在公共点（0，y 0）处有相同的切线，（i ）求证：()f x 在0x x =处的导数等于0；（ii ）若关于的不等式()e x g x ≤在区间00[1,1]x x -+上恒成立，求b 的取值范围．【答案】（Ⅰ）递增区间为(,)a -∞，(4,)a -+∞，递减区间为(),4a a -；（Ⅱ）（ⅰ）见解析，（ⅱ）[7],1-．【解析】（Ⅰ）由324()63()f x x a x x a b =--+-，可得2()3123()3()((44))f 'x x a x a a x x a -=---=--，令()0f 'x =，解得x a =或4x a =-．由||1a ≤，得4a a <-． 当x 变化时，()f 'x ，()f x 的变化情况如下表：所以，()f x 的单调递增区间为(,)a -∞，(4,)a -+∞，单调递减区间为(),4a a -．（Ⅱ）（i ）因为()e (()())x x x g'f f 'x =+，由题意知00()e ()e x x x x g g'⎧=⎪⎨=⎪⎩， 所以000000()e e e (()())ex x xx f f f x 'x x ⎧=⎪⎨+=⎪⎩，解得00()1()0f 'x x f =⎧⎨=⎩． 所以，()f x 在0x x =处的导数等于0．（ii ）因为()e xg x ≤，00[11],x x x ∈-+，由e 0x >，可得()1f x ≤．又因为0()1f x =，0()0f 'x =，故0x 为()f x 的极大值点，由（Ⅰ）知0x a =． 另一方面，由于||1a ≤，故14a a +<-，由（Ⅰ）知()f x 在(,)1a a -内单调递增，在(),1a a +内单调递减， 故当0x a =时，()()1f f x a ≤=在[1,1]a a -+上恒成立，从而()e xg x ≤在00,[11]x x -+上恒成立．由32()63()14a a f a a a a b =---+=，得32261b a a =-+，11a -≤≤．令32()261t x x x =-+，[1,1]x ∈-，所以2()612t'x x x =-，令()0t'x =，解得2x =（舍去），或0x =． 因为(1)7t -=-，(1)3t =-，(0)1t =， 故()t x 的值域为[7],1-． 所以，b 的取值范围是[7],1-．【名师点睛】本题考查导数的应用，属于中档问题，第一问的关键是根据条件判断两个极值点的大小，从而避免讨论；第二问要注意切点是公共点，切点处的导数相等，求b 的取值范围的关键是得出0x a =，然后构造函数进行求解．22．【2017年高考山东文数】已知函数()3211,32f x x ax a =-∈R . （Ⅰ）当a =2时,求曲线()y f x =在点()()3,3f 处的切线方程；（Ⅱ）设函数()()()cos sin g x f x x a x x =+--,讨论()g x 的单调性并判断有无极值,有极值时求出极值.【答案】（Ⅰ）390x y --=,（Ⅱ）见解析.【解析】（Ⅰ）由题意2()f x x ax '=-，所以，当2a =时，(3)0f =，2()2f x x x '=-， 所以(3)3f '=，因此，曲线()y f x =在点(3,(3))f 处的切线方程是3(3)y x =-， 即390x y --=.（Ⅱ）因为()()()cos sin g x f x x a x x =+--， 所以()()cos ()sin cos g x f x x x a x x ''=+---，()()sin x x a x a x =--- ()(sin )x a x x =--，令()sin h x x x =-， 则()1cos 0h x x '=-≥， 所以()h x 在R 上单调递增， 因为(0)0h =，所以，当0x >时，()0h x >；当0x <时，()0h x <. （1）当0a <时，()()(sin )g x x a x x '=--，当(,)x a ∈-∞时，0x a -<，()0g x '>，()g x 单调递增； 当(,0)x a ∈时，0x a ->，()0g x '<，()g x 单调递减； 当(0,)x ∈+∞时，0x a ->，()0g x '>，()g x 单调递增. 所以当x a =时()g x 取到极大值，极大值是31()sin 6g a a a =--，当0x =时()g x 取到极小值，极小值是(0)g a =-. （2）当0a =时，()(sin )g x x x x '=-， 当(,)x ∈-∞+∞时，()0g x '≥，()g x 单调递增；所以()g x 在(,)-∞+∞上单调递增，()g x 无极大值也无极小值. （3）当0a >时，()()(sin )g x x a x x '=--，当(,0)x ∈-∞时，0x a -<，()0g x '>，()g x 单调递增； 当(0,)x a ∈时，0x a -<，()0g x '<，()g x 单调递减； 当(,)x a ∈+∞时，0x a ->，()0g x '>，()g x 单调递增. 所以当0x =时()g x 取到极大值，极大值是(0)g a =-； 当x a =时()g x 取到极小值，极小值是31()sin 6g a a a =--. 综上所述：当0a <时，函数()g x 在(,)a -∞和(0,)+∞上单调递增，在(,0)a 上单调递减，函数既有极大值，又有极小值，极大值是31()sin 6g a a a =--，极小值是(0)g a =-； 当0a =时，函数()g x 在(,)-∞+∞上单调递增，无极值；当0a >时，函数()g x 在(,0)-∞和(,)a +∞上单调递增，在(0,)a 上单调递减，函数既有极大值，又有极小值，极大值是(0)g a =-，极小值是31()sin 6g a a a =--. 【名师点睛】(1)求函数f ()极值的步骤：①确定函数的定义域；②求导数f ′()；③解方程f ′()＝0,求出函数定义域内的所有根；④检验f ′()在f ′()＝0的根0左右两侧值的符号,如果左正右负,那么f ()在0处取极大值,如果左负右正,那么f ()在0处取极小值．(2)若函数y ＝f ()在区间(a ,b )内有极值,那么y ＝f ()在(a ,b )内绝不是单调函数,即在某区间上单调函数没有极值．23．【2017年高考江苏】已知函数32()1(0,)f x x ax bx a b =+++>∈R 有极值，且导函数()'f x 的极值点是()f x 的零点．（极值点是指函数取极值时对应的自变量的值） （1）求b 关于a 的函数关系式，并写出定义域； （2）证明：23>b a ；（3）若()f x ，()'f x 这两个函数的所有极值之和不小于72-，求a 的取值范围．【答案】（1）2239a b a=+，定义域为(3,)+∞；（2）见解析；（3）(36]，． 【解析】（1）由32()1f x x ax bx =+++，得222()323()33a a f x x axb x b '=++=++-．当3a x =-时，()f x '有极小值23ab -．因为()f x '的极值点是()f x 的零点．所以33()1032793a a a abf -=-+-+=，又0a >，故2239a b a=+．因为()f x 有极值，故()=0f x '有实根，从而231(27)039a b a a-=-≤，即3a ≥．当3a =时，()>0(1)f x x '≠-，故()f x 在R 上是增函数，()f x 没有极值；当3a >时，()=0f x '有两个相异的实根1=3a x --，2=3a x -．列表如下：故()f x 的极值点是12,x x ． 从而3a >．因此2239a b a=+，定义域为(3,)+∞．（2）由（129． 设23()=9t g t t +，则22223227()=99t g t t t-'-=．当)t ∈+∞时，()0g t '>，从而()g t 在)+∞上单调递增．因为3a >，所以>故(g g因此2>3b a ．（3）由（1）知，()f x 的极值点是12,x x ， 且1223x x a +=-，22212469a b x x -+=． 从而323212111222()()11f x f x x ax bx x ax bx +=+++++++2222121122121212(32)(32)()()23333x x x ax b x ax b a x x b x x =++++++++++ 346420.279a ab ab -=-+= 记()f x ，()f x '所有极值之和为()h a ，因为()f x '的极值为221339a b a a-=-+，所以213()=9h a a a -+，3a >． 因为223()=09h a a a'--<，于是()h a 在(3,)+∞上单调递减． 因为7(6)=2h -，于是()(6)h a h ≥， 故6a ≤．因此a 的取值范围为(36]，． 【名师点睛】涉及函数的零点问题、方程解的个数问题、函数图象的交点个数问题，一般先通过导数研究函数的单调性、最大值、最小值、变化趋势等，再借助函数的大致图象判断零点、方程根、交点的情况，归根到底还是研究函数的性质，如单调性、极值，然后通过数形结合的思想找到解题的思路．。
20122017年高考文科数学真题汇编坐标系和参数方程老师版
学科教师辅导教案 学员姓名 年 级高三 辅导科目 数 学授课老师课时数2h第 次课授课日期及时段 2017年 月 日 ： — ：1.（2015年广东文）在平面直角坐标系x y O 中，以原点O 为极点，x 轴的正半轴为极轴建立极坐标系．曲线1C 的极坐标方程为()cos sin 2ρθθ+=-，曲线2C 的参数方程为222x ty t⎧=⎪⎨=⎪⎩（t 为参数），则1C 与2C 交点的直角坐标为 ()2,4- ．2.（2015年新课标2文）在直角坐标系xOy 中,曲线1cos ,:sin ,x t C y t αα=⎧⎨=⎩（t 为参数,且0t ≠ ）,其中0απ≤<,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线23:2sin ,:23cos .C C ρθρθ==（I ）求2C 与3C 交点的直角坐标； （II ）若1C 与 2C 相交于点A ,1C 与3C 相交于点B ,求AB 最大值.试题分析：（I ）把2C 与3C 的方程化为直角坐标方程分别为2220x y y +-=,22230x y x +-=,联立解历年高考试题集锦——坐标系和参数方程3.（2015年陕西文）在直角坐标版权法xOy 吕，直线l 的参数方程为132(32x t t y t ⎧=+⎪⎪⎨⎪=⎪⎩为参数），以原点为极点，x 轴的正半轴为极轴建立极坐标系，C e 的极坐标方程为23sin ρθ=.(I)写出C e 的直角坐标方程；(II)P 为直线l 上一动点，当P 到圆心C 的距离最小时，求点P 的坐标.试题解析：(I)由23sin ρθ=，得223sin ρρθ=，从而有2223x y y +=所以()2233x y +-=(II)设133,22P t t ⎛⎫+ ⎪⎝⎭，又(0,3)C ，则22213331222PC t t t ⎛⎫⎛⎫=++-=+ ⎪ ⎪⎝⎭⎝⎭，故当0t =时，PC 取得最小值，此时P 点的坐标为(3,0).4、（2015新课标1）在直角坐标系xOy 中，直线1:2C x =-，圆()()222:121C x y -+-=，以坐标原点为极点,x 轴正半轴为极轴建立极坐标系. （I ）求12,C C 的极坐标方程. （II ）若直线3C 的极坐标方程为()πR 4θρ=∈，设23,C C 的交点为,M N ，求2C MN ∆ 的面积. 解：（I ）因为cos ,sin x y ρθρθ==，所以1C 的极坐标方程为cos 2ρθ=-，2C 的极坐标方程为22cos 4sin 40ρρθρθ--+=. ……5分（II ）将4πθ=代入22cos 4sin 40ρρθρθ--+=，得23240ρρ-+=，解得1222,2ρρ==.故122ρρ-=，即2MN =由于2C 的半径为1，所以2C MN ∆的面积为12.5、（2016年全国I ）在直角坐标系xOy 中，曲线C 1的参数方程为（t 为参数，a ＞0）.在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线C 2：ρ=4cos θ. （I ）说明C 1是哪种曲线，并将C 1的方程化为极坐标方程；（II ）直线C 3的极坐标方程为θ=α0，其中α0满足tan α0=2，若曲线C 1与C 2的公共点都在C 3上，求a . 解：⑴ cos 1sin x a t y a t=⎧⎨=+⎩ （t 均为参数）∴()2221x y a +-= ①∴1C 为以()01，为圆心，a 为半径的圆．方程为222210x y y a +-+-=∵222sin x y y ρρθ+==，∴222sin 10a ρρθ-+-=即为1C 的极坐标方程⑵ 24cos C ρθ=：两边同乘ρ得22224cos cos x y x ρρθρρθ==+=Q ，224x y x ∴+=即()2224x y -+= ②3C ：化为普通方程为2y x =由题意：1C 和2C 的公共方程所在直线即为3C ①—②得：24210x y a -+-=，即为3C ∴210a -=∴1a =6、（2016年全国II ）在直角坐标系xOy 中，圆C 的方程为22(6)25x y ++=． （Ⅰ）以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，求C 的极坐标方程；（Ⅱ）直线l 的参数方程是cos sin x t y t αα=⎧⎨=⎩（t 为参数）, l 与C 交于,A B 两点，||10AB =，求l 的斜率．解：⑴整理圆的方程得2212110x y +++=，由222cos sin x y x y ρρθρθ⎧=+⎪=⎨⎪=⎩可知圆C 的极坐标方程为212cos 110ρρθ++=．⑵记直线的斜率为k ，则直线的方程为0kx y -=，由垂径定理及点到直线距离公式知：226102521kk ⎛⎫-=- ⎪ ⎪+⎝⎭， 即22369014k k =+，整理得253k =，则153k =±． 7、（2016年全国III ）在直角坐标系xOy 中，曲线1C 的参数方程为3cos ()sin x y θθθ⎧=⎪⎨=⎪⎩为参数，以坐标原点为极点，以x 轴的正半轴为极轴，，建立极坐标系，曲线2C 的极坐标方程为sin()224ρθπ+= .（I ）写出1C 的普通方程和2C 的直角坐标方程；（II ）设点P 在1C 上，点Q 在2C 上，求|PQ |的最小值及此时P 的直角坐标.8、(2016江苏)在平面直角坐标系xOy 中，已知直线l 的参数方程为11232x t y t ⎧=+⎪⎪⎨⎪=⎪⎩ （t 为参数），椭圆C 的参数方程为cos ,2sin x y θθ=⎧⎨=⎩ （θ为参数）.设直线l 与椭圆C 相交于A ，B 两点，求线段AB 的长.解：椭圆C 的普通方程为2214y x +=，将直线l 的参数方程11232x t y t⎧=+⎪⎪⎨⎪=⎪⎩，代入2214y x +=，得223()12(1)124t t ++=，即27160t t +=，解得10t =，2167t =-.所以1216||7AB t t =-=.9．（2013江苏理）在平面直角坐标系xoy 中，直线l 的参数方程为⎩⎨⎧=+=t y t x 21（t 为参数），曲线C 的参数方程为⎩⎨⎧==θθtan 2tan 22y x （θ为参数），试求直线l 与曲线C 的普通方程，并求出它们的公共点的坐标。
高考文科数学真题汇编：导数及应用老师版.doc
2012-2017 年高考文科数学真题汇编：导数及应用老师版学科教师辅导教案学员姓名年级高三辅导科目数学授课老师课时数2h 第次课授课日期及时段2018 年月日：—：历年高考试题汇编（文）——导数及应用1．（2014 大纲理）曲线y xe x 1在点（1,1）处切线的斜率等于（ C ）A ．2e B．e C．2D．12.(2014 新标 2 理) 设曲线 y=ax-ln(x+1) 在点 (0,0)处的切线方程为 y=2x，则 a= （ D ）A. 0B. 1C. 2D. 33.( 2013 浙江文 ) 已知函数 y＝f(x)的图象是下列四个图象之一，且其导函数 y＝f′(x)的图象如右图所示，则该函数的图象是 ( B )4．（2012 陕西文）设函数 f（x）= 2x +lnx 则（ D ）A ．x= 1为 f(x) 的极大值点B．x= 1为f(x) 的极小值点C．x=2 为 f(x) 的极大值点D．x=2 为 f(x) 的极小值点5.(2014 新标 2 文) 函数f (x)在x x0 处导数存在，若p : f ( x0 )0 ：q : x x0是 f ( x) 的极值点，则A ．p是q的充分必要条件 B. p是q的充分条件，但不是 q 的必要条件C. p是q的必要条件，但不是q的充分条件D. p既不是 q 的充分条件，也不是 q 的必要条件【答案】 C6．（2012 广东理）曲线y x3 x 3 在点 1,3 处的切线方程为___________________.【答案】 2x-y+1=07．（2013 广东理）若曲线y kx ln x 在点 (1,k) 处的切线平行于x 轴，则k【答案】 -18．（2013 广东文）若曲线y ax2 ln x 在点 (1,a) 处的切线平行于 x 轴，则 a ．【答案】1 29 ． ( 2014 广东文 ) 曲线y 5 e x 3 在点 (0, 2) 处的切线方程为.【答案】 5x+y+2=010．（2013 江西文）若曲线 y= xα +1（α∈ R）在点（ 1，2）处的切线经过坐标原点，则α=。
2012-2017年高考文科数学真题汇编：直线和圆老师版(最新整理)
95 4 3
x
3
；
31（2016 年新课标 1 理）设圆 x2 y2 2x 15 0 的圆心为 A，直线 l 过点 B（1,0）且与 x 轴不重合，l
交圆 A 于 C，D 两点，过 B 作 AC 的平行线交 AD 于点 E.（I）证明 EA EB 为定值，并写出点 E 的轨迹
方程。
【详细解答】（I）圆心为 A(1, 0) ，圆的半径为 AD 4 ， AD AC ，
22.（2015 北京文）圆心为 1,1 且过原点的圆的方程是（ D ）
A． x 12 y 12 1
B． x 12 y 12 1
C． x 12 y 12 2
D． x 12 y 12 2
23.（2015 年广东理）平行于直线 2x y 1 0 且与圆 x2 y2 5 相切的直线的方程是（ D ）
学员姓名 授课老师
授课日期及时段
学科教师辅导教案
年级
高三
辅导科目
课时数
2h
第
2017 年 月 日 ： — ：
数学 次课
历年高考试题集锦——直线和圆
1．（2012 辽宁文）将圆 x2+y2 -2x-4y+1=0 平分的直线是（ C ）
（A）x）x-y+1=0 （D）x-y+3=0
4 的距离为
5 ，则圆 C 的方程为____ (x 2)2 y2 9. ______
5
19、（2016 年全国 I 卷）设直线 y=x+2a 与圆 C：x2+y2-2ay-2=0 相交于 A，B 两点，若
，则圆 C
的面积为 4π . 20、（2016 年全国 III 卷）已知直线 l ： x 3y 6 0 与圆 x2 y2 12 交于 A, B 两点，过 A, B 分别作 l
2012-2017年高考文科数学真题汇编：圆锥曲线老师版
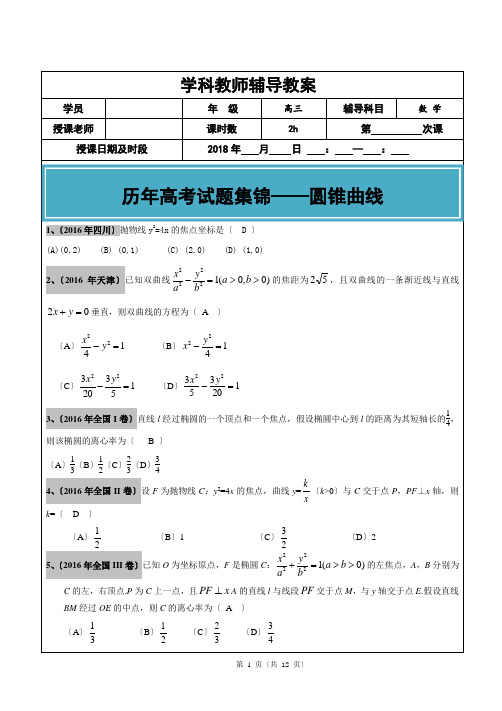
〔Ⅱ〕因为AB 过点(1,0)D 且垂直于x 轴，所以可设1(1,)A y ，1(1,)B y -. 直线AE 的方程为11(1)(2)y y x -=--.令3x =，得1(3,2)M y -. 所以直线BM 的斜率112131BM y y k -+==-.17.〔2015年安徽文〕设椭圆E 的方程为22221(0),x y a b a b+=>>点O 为坐标原点，点A 的坐标为(,0)a ,点B 的坐标为〔0，b 〕,点M 在线段AB 上，满足2,BM MA =直线OM 的斜率为510。
[学优高考网]〔1〕求E 的离心率e;(2)设点C 的坐标为〔0，-b 〕,N 为线段AC 的中点，证明：MN ⊥AB 。
∴a b3231＝5525451511052222222=⇒=⇒=-⇒=⇒e a c a c a a b〔Ⅱ〕由题意可知N 点的坐标为〔2,2b a -〕∴a b a ba a bb K MN 56652322131==-+= abK AB-=∴1522-=-=⋅a b K K AB MN ∴MN ⊥AB18.〔2015年福建文〕已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为F ．短轴的一个端点为M ，直线:340l x y -=交椭圆E 于,A B 两点．假设4AF BF +=，点M 到直线l 的距离不小于45，则椭圆E 的离心率的取值范围是〔 A 〕 A ． 3(0,]2 B ．3(0,]4 C ．3[,1)2 D ．3[,1)4119.〔2015年新课标2文〕已知双曲线过点()4,3,且渐近线方程为12y x =±,则该双曲线的标准方程为 ．2214x y -= 20.〔2015年陕西文〕已知抛物线22(0)y px p =>的准线经过点(1,1)-，则抛物线焦点坐标为〔 B 〕 A ．(1,0)- B ．(1,0) C ．(0,1)- D ．(0,1) 【解析】试题分析：由抛物线22(0)y px p =>得准线2px =-，因为准线经过点(1,1)-，所以2p =， 所以抛物线焦点坐标为(1,0)，故答案选B 考点：抛物线方程.21.〔2015年陕西文科〕如图，椭圆2222:1(0)x y E a b a b+=>>经过点(0,1)A -，且离心率为22.(I)求椭圆E 的方程；2212x y += 22.〔2015年天津文〕已知双曲线22221(0,0)x y a b ab 的一个焦点为(2,0)F ,且双曲线的渐近线与圆222y 3x 相切,则双曲线的方程为〔 D 〕(A)221913x y (B) 221139x y (C)2213x y(D) 2213y x的等腰三角形，则新标2文221y b 0,0a b 的一条渐近线平行于直线210x ，双曲上，则双曲线的方程为〔 A 〕2120y 〔B 〕221205x y 〔C 〕2233125100x y 2233110025x y新标1) 已知双曲线2221x y =〔0,0a b >>〕的离心率为52，则14x B .13y =±12x ± D .y x[9,)+∞[9,)+∞C ．(0,1][4,)+∞D ．(0,3][4,)+∞【答案】A 【解析】当03m <<，焦点在x 轴上，要使C 上存在点M 满足120AMB ∠=，则tan 603ab≥=，即33m≥，得01m <≤；当3m >，焦点在y 轴上，要使C 上存在点M 满足120AMB ∠=，则tan 603a b ≥=，即33m ≥，得9m ≥，故m 的取值范围为(0,1][9,)⋃+∞，选A. 41、(2017·全国Ⅱ文，5)假设a >1，则双曲线x 2a 2－y 2＝1的离心率的取值范围是( )A ．(2，＋∞)B ．(2，2)C ．(1，2)D ．(1,2)3．【答案】C 【解析】由题意得双曲线的离心率e ＝a 2＋1a .∴e 2＝a 2＋1a 2＝1＋1a 2.∵a ＞1，∴0＜1a 2＜1，∴1＜1＋1a2＜2，∴1＜e ＜ 2.故选C.42．(2017·全国Ⅱ文，12)过抛物线C ：y 2＝4x 的焦点F ，且斜率为3的直线交C 于点M (M 在x 轴上方)，l 为C 的准线，点N 在l 上且MN ⊥l ，则M 到直线NF 的距离为( )A. 5 B ．2 2 C ．2 3 D ．3 34．【答案】C 【解析】抛物线y 2＝4x 的焦点为F (1,0)，准线方程为xMF 的方程为y ＝3(x －1)．联立得方程组⎩⎨⎧y ＝3(x －1)，y 2＝4x ，解得⎩⎨⎧x ＝13，y ＝－233或⎩⎨⎧x ＝3，y ＝2 3.∵点M 在x 轴的上方，∴M (3,23)．∵MN ⊥l ，∴N (－1,23)．∴|NF |＝(1＋1)2＋(0－23)2＝4， |MF |＝|MN |＝3－(－1)＝4.∴△MNF 是边长为4的等边三角形．∴点M 到直线NF 的距离为2 3. 故选C.43．(2017·全国Ⅲ文，11)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线bx －ay ＋2ab ＝0相切，则椭圆C 的离心率为( ) A ．63 B ．33 C ．23 D ．135．【答案】A 【解析】由题意知以A 1A 2为直径的圆的圆心坐标为(0,0)，半径为a .又直线bx －ay ＋2ab ＝0与圆相切，∴圆心到直线的距离d ＝2aba 2＋b 2＝a ，解得a ＝3b ， ∴b a ＝13，∴e ＝ca ＝a 2－b 2a ＝ 1－⎝⎛⎭⎫b a 2＝1－⎝⎛⎭⎫132＝63. 44．(2017·天津文，5)已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的右焦点为F ，点A 在双曲线的渐近线上，△OAF是边长为2的等边三角形(O 为原点)，则双曲线的方程为( ) A ．x 24－y 212＝1B ．x 212－y 24＝1C ．x 23－y 2＝1D ．x 2－y 23＝1 6．【答案】D 【解析】根据题意画出草图如下图⎝⎛⎭⎫不妨设点A 在渐近线y ＝ba x 上.由△AOF 是边长为2的等边三角形得到∠AOF ＝60°，c ＝|OF A 在双曲线的渐近线y ＝b a x 上，∴ba ＝tan 60°＝ 3.又a 2＋b 2＝4，∴a ＝1，b ＝3，∴双曲线的方程为x 2－y 23＝1.故选D. 45．(2017·全国Ⅲ文，14)双曲线x 2a 2－y 29＝1(a >0)的一条渐近线方程为y ＝35x ，则a ＝________.1．【答案】5【解析】∵双曲线的标准方程为x 2a 2－y 29＝1(a ＞0)，∴双曲线的渐近线方程为y ＝±3a x .又双曲线的一条渐近线方程为y ＝35x ，∴a ＝5.46、(2017·北京文，10)假设双曲线x 2－y 2m＝1的离心率为3，则实数m ＝________. 【答案】2【解析】由双曲线的标准方程知a ＝1，b 2＝m ，c ＝1＋m ，故双曲线的离心率e ＝ca ＝1＋m ＝3，∴1＋m ＝3，∴m ＝2.47、(2017·全国Ⅱ理，16)已知F 是抛物线C ：y 2＝8x 的焦点，M 是C 上一点，FM 的延长线交y 轴于点N .假设M 为FN 的中点，则|FN |＝________.【解析】如图，不妨设点M 位于第一象限内，抛物线C 的准线交x 轴于点A ，过点M 作准线的垂线，垂足为点B ，交y 轴于点P ，∴PM ∥OF .由题意知，F (2,0)，|FO |＝|AO |＝2.∵点M 为FN 的中点，PM ∥OF ，∴|MP |＝12|FO |＝1.又|BP |＝|AO |＝2，∴|MB |＝|MP |＋|BP |＝3.由抛物线的定义知|MF |＝|MB |＝3，故|FN |＝2|MF |＝6.48、(2017新课标1文)设A ，B 为曲线C ：y =24x 上两点，A 与B 的横坐标之和为4.〔1〕求直线AB 的斜率；〔2〕设M 为曲线C 上一点，C 在M 处的切线与直线AB 平行，且AM ⊥BM ，求直线AB 的方程. 【解析】〔1〕设()()1122,,,A x y B x y ，则2221212121214414AB x x y y x x K x x x x --+====-- 〔2〕设200,4x M x ⎛⎫ ⎪⎝⎭，则C 在M 处的切线斜率'00112AB y K K x x x ====- ∴02x = 则()12,1A ，又AM ⊥BM ，22121212121111442222AM BMx x y y K K x x x x ----==---- ()()()121212222411616x x x x x x +++++===-即()12122200x x x x +++= 又设AB ：y=x ＋m 代入24x y = 得2440x x m --= ∴124x x +=，124x x m =- －4m ＋8＋20=0∴m=7故AB ：x ＋y=749.(2017年新课标Ⅱ文)设O 为坐标原点,动点M 在椭圆C :x 22＋y 2＝1上，过M 作x 轴的垂线,垂足为N ,点P满足→NP ＝2→NM . (1)求点P 的轨迹方程；(2)设点Q 在直线x ＝－3上,且→OP ·→PQ ＝1.证明:过点P 且垂直于OQ 的直线l 过C 的左焦点F . 【解析】(1)设P (x ,y ),M (x 0,y 0),则N (x 0,0),→NP ＝(x －x 0,y ),→NM ＝(0,y 0).由→NP ＝2→NM 得x 0＝x ,y 0＝22y .∵M (x 0,y 0)在C 上,∴x 22＋y 22＝1,∴点P 的轨迹方程为x 2＋y 2＝2.(2)由题意知F (－1,0).设Q (－3,t ),P (m ,n ),则→OQ ＝Q (－3,t ),→PF ＝(－1－m ,－n ),→OQ ·→PF ＝3＋3m －tn , →OP ＝(m ,n ),→PQ ＝(－3－m ,－tn ).由→OP ·→PQ ＝1得－3m －m 2＋tn －n 2＝1,。
2012-2017年高考文科数学真题汇编：解三角形高考题老师版
学科教师辅导教案学员姓名年 级高三 辅导科目 数 学授课老师课时数2h第 次课授课日期及时段 2018年 月 日 ： — ：1．（2017新课标Ⅲ文）△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知C =60°，b =6，c =3，则A =__ 75°_。
2．(2012广东文) 在ABC ∆中，若60,45,32A B BC ︒︒∠=∠==，则AC =( B )()A 43 ()B 23 ()C 3 ()D 323．（2013湖南）在锐角中ABC ∆，角,A B 所对的边长分别为,a b .若2sin 3,a B b A =则角等于（ D ） A ．12π B ．6π C ．4π D ．3π 4．(2013湖南文)在∆ABC 中，角A ，B 所对的边长分别为a ，b. 若2asinB=3b ，则角A 等于（ A ） A .3π或32π B .4π或43π C .3π D .32π 5．(2014江西理) 在ABC ∆中，内角A,B,C 所对应的边分别为,,,c b a ，若,3,6)(22π=+-=C b a c 则ABC ∆的面积（ C ）A.3B.239C.233 D.336．（2014江西文）在在ABC ∆中，内角A,B,C 所对应的边分别为,,,c b a ，若35a b =，则2222sin sin sin B AA-的值为（ D ） 1.9A - 1.3B .1C 257.D -7．（2017新课标1文）11．△ABC 的内角A 、B 、C 的对边分别为a 、b 、c 。
已知sin sin (sin cos )0B A C C +-=，a =2，c =2，则C =A ．π12B ．π6C ．π4D ．π3【答案】B 【解析】由题意sin()sin (sin cos )0A C A C C ++-=得sin cos cos sin sin sin sin cos 0A C A C A C A C ++-=，历年高考试题集锦（文）——解三角形即sin (sin cos )2sin sin()04C A A C A π+=+=，所以34A π=. 由正弦定理sin sin a c A C =得223sin sin 4C π=，即1sin 2C =，得6C π=，故选B. 8．（2012上海）在ABC ∆中，若C B A 222sin sin sin <+，则ABC ∆的形状是（ C ）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不能确定9.（2013天津理）在△ABC 中，∠ABC ＝π4，AB ＝2，BC ＝3，则sin ∠BAC 等于( C )A.1010 B.105 C.31010 D.5510.(2013新标2文) △ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知b ＝2，B ＝π6，c ＝π4，则△ABC的面积为( B ) A ．23＋2B.3＋1 C ．23－2D.3－111、(2013新标1文) 已知锐角ABC ∆的内角,,A B C 的对边分别为,,a b c ，223cos cos 20A A +=，7a =，6c =，则b =（ D ）（A ）10 （B ）9（C ）8（D ）512．（2013辽宁）在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c .若a sin B cos C ＋c sin B cos A ＝12b ，且a ＞b ，则∠B ＝( ) A.π6B.π3C.2π3D.5π6【简解】由条件得a b sin B cos C ＋c b sin B cos A ＝12， sin A cos C ＋sin C cos A ＝12，∴sin(A ＋C )＝12，从而sin B＝12，又a ＞b ，且B ∈(0，π)，因此B ＝π6.选A 13．（2013山东文）△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c .若B ＝2A ，a ＝1，b ＝3，则c ＝( )A ．2 3B ．2 C. 2D ．1【简解】由正弦定理得：1sin A ＝3sin B ＝3sin 2A ＝32sin A cos A .，cos A ＝32，A ＝30°，B ＝60°，C ＝90°，所以c 2＝a 2＋b 2＝4，所以c ＝2.14．（2013陕西）设△ABC 的内角A, B, C 所对的边分别为a, b, c, 若cos cos sin b C c B a A +=, 则△ABC 的形状为 (A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 不确定 【简解】sinBcosC+sinCcosB=sinAsinA,sin(B+C)=sin 2A,sinA=1,A=2π.选B 15、（2016年新课标Ⅰ卷文）△ABC 的内角A 、B 、C 的对边分别为a 、b 、c.已知5a =，2c =，2cos3A=，则b=（A）2（B）3（C）2 （D）3【答案】D16、（2016年新课标Ⅲ卷文）在ABC△中，π4B，BC边上的高等于13BC,则sin A（A）310（B）1010（C）55（D）31010试题分析：设BC边上的高线为AD，则3,2BC AD DC AD==，所以225AC AD DC AD=+=．由正弦定理，知sin sinAC BCB A=，即53sin22AD ADA=，解得310sin10A=，故选D．17、（2016年高考山东卷文）ABC△中，角A，B，C的对边分别是a，b，c，已知22,2(1sin)b c a b A,则A=（A）3π4（B）π3（C）π4（D）π6【答案】C考点：余弦定理18、2016年高考北京卷文)在△ABC中，23Aπ∠=，a=3c，则bc=_________.试题分析：由正弦定理知sin3sinA aC c==，所以2sin13sin23Cπ==，则6Cπ=，所以2366Bππππ=--=，所以b c=，即1bc=．考点：解三角形19、（2016年新课标Ⅱ卷文）△ABC的内角A，B，C的对边分别为a，b，c，若4cos5A=，5cos 13C =，a =1，则b =____________. 【解析】因为45cos ,cos 513A C ==，且,A C 为三角形内角，所以312sin ,sin 513A C ==，13sin sin(C)sin cos cos sin 65B A AC A C =+=+=，又因为sin sin a b A B =，所以sin 21sin 13a Bb A ==.20．（2013安徽）设ABC ∆的内角,,A B C 所对边的长分别为,,a b c 。
2012-2017年高考文科数学真题汇编：坐标系和参数方程老师版
学 科 教 师 辅 导 教 案授课日期及时段2017年月日：一1.（ 2015年广东文）线G 的极坐标方程为 ?COST sinv - -2,曲线C 2的参数方程为X" （ t 为参数），则c ,与C 2交[y =2（2txOy 中，曲线 G ： x-tcos- ,（t 为参数，且t = o ）, y =tsinot,,在以o 为极点,x 轴正半轴为极轴的极坐标系中，曲线C 2 ： ' = 2sin 二，C 3:『=2 3cos .（I ）求C 2与C 3交点的直角坐标；（II ）若C ,与C 2相交于点A C i 与C 3相交于 点B ,求AB 最大值.试题分析：（I ）把C 2与C 3的方程化为直角坐标方程分别为X 2 y 2-2y =0,x 2 y 2 - 2 - 3^0, 联 立 解学员姓名 年级咼二辅导科目 数学授课老师课时数2h第次课建立极坐标系.曲点的直角坐标为 2, -4 .其中 0 _ ：方程溟可帚玄毛住届 5)元踴定田连q 跆捋方程为&二列尸怎比口砂〕起一步求比点4田股生标 先(24n 蔭.cr ］点3的赣坐标为:2^3阳cc rxj 由lit 可届 |-切| ==4 sin ； a~—；I I »tv.门】曲纯G 的劃i 坐标才程为討+H -即"堆錢C 的臣角坐标2隍为Y 3 +j :- 烬=0慝注T孑百3、：厨以G 写Q 喪点的直审业悟［0』片丄二訂di: it 或G 粧生标古里対■立耳中。
三空v-兀 因i 汽亠田槻坐咄利2血尤②車g以坐标原点为极点，X 轴正半轴为极轴建立极坐标系(I )求C i ,C 2的极坐标方程.(II )若直线C 3的极坐标方程为日=』(PE R )，设C 2,C 3的交点为M,N ，求A C 2MN1;■ I=sidff-—xOy 吕，直线I 的参数方程为］x = 3十」t占2 (t 为参数)，以原点为极点，X 轴的正半轴为极轴建立极坐标系， L C 的极坐标方程为二=2 3sinx⑴ 写出L C 的直角坐标方程;(II) 为求点P 的坐标.试题解析： ⑴ 由—2、：3sinr ,得「2=2、.3飞inn ，从而有x 2 亠〔y - ；3 = 3卡寸二2 3y 所以 (II)设+号呼「『3昇卜A 2丿<2 丿t 2 12 , 故当t =0时，PC 取得最小值，此时P 点的坐标为(3,0).4、(2015新课标1)在直角坐标系xOy 中，直线C i:x = -2 ,圆 C2：(x-1$+(y -2)2=1 ,兰口=苓时⑷限待醍人直醍尢值拘1. 6Hi以「iff | - |2si]i!Z-2^ UJ > L £(I)以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求C的极坐标方程；（H ）直线l 的参数方程是[xicosc ^t 为参数），|与C 交于A ,B 两点，|AB|=V10 , y = tsi na求l 的斜率. f = x 2• y 2解：⑴整理圆的方程得x 2y 212 1^0，由Tcosv-x 可知圆C 的极坐标"sin J - y方程为J 2 12 2osr 1仁0 .⑵记直线的斜率为k ，则直线的方程为kx — y=0， 由垂径定理及点到直线距离公式知：単=丄5 一回f , 即、时' I 2丿36k ： =90，整理得 k 2=5，则—15 . 1 k 24 337、（ 2016年全国III ）在直角坐标系xOy 中，曲线C 1的参数方程为日（日为参数）, [y =s in 日以坐标原点为极点，以x 轴的正半轴为极轴，，建立极坐标系，曲线C 2的 极坐标方程为宀心尸2（I ）写出C 1的普通方程和C 2的直角坐标方程；（II ）设点P 在C 1上，点Q 在C 2上，求|PQ 的最小值及此时P 的直角坐8、（2016江苏）在平面直角坐标系xOy 中，已知直线I 的参数方程为x =cos 入厂2sin '（二为参数）.设直线|与椭圆C 相 交于A, B两点，求线段AB 的长.x =1 - t23 F (t为参数），椭圆C 的参数方程为通方程，并求出它们的公共点的坐标。
20122017年高考文科数学真题汇编：坐标系和参数方程老师版.doc
C的极坐标方程为C的直角坐标方程；为直线l上一动点，当到圆心C的距离最小时，求点ρ=(I)由2：化为普通方程为2=由题意：y x，（I ）求直线l 和圆C 的普通方程；（II ）若直线l 与圆C 有公共点，求实数a 的取值范围.【简解】（I ）直线l 的普通方程为220x y a --=.圆C 的普通方程为2216x y +=. （II ）因为直线l 与圆有公共点,故圆C 的圆心到直线l 的距离245a d -=≤,解得2525a -≤≤12. (2014新标1理)已知曲线C ：22149x y +=，直线l ：222x t y t =+⎧⎨=-⎩（t 为参数）. (Ⅰ)写出曲线C 的参数方程，直线l 的普通方程；（Ⅱ）过曲线C 上任一点P 作与l 夹角为o30的直线，交l 于点A ，求||PA 的最大值与最小值. 【简解】.(Ⅰ) 曲线C 的参数方程为：2cos 3sin x y θθ=⎧⎨=⎩（θ为参数）， 直线l 的普通方程为：260x y +-=（Ⅱ）在曲线C 上任意取一点P (2cos θ,3sin θ)到l 的距离为54cos 3sin 65d θθ=+-， 则()025||5sin 6sin 305d PA θα==+-，其中α为锐角．且4tan 3α=. 当()sin 1θα+=-时，||PA 取得最大值，最大值为2255； 当()sin 1θα+=时，||PA 取得最小值，最小值为255. 13.(2013新标2理)已知动点P 、Q 都在曲线C ：2cos 2sin x ty t =⎧⎨=⎩(t 为参数)上，对应参数分别为t ＝α与t ＝2α(0<α<2π)，M 为PQ 的中点．(1)求M 的轨迹的参数方程； (2)将M 到坐标原点的距离d 表示为α的函数，并判断M 的轨迹是否过坐标原点． 【简解】 (1)依题意有P (2cos α，2sin α)，Q (2cos 2α，2sin 2α)，因此M (cos α＋cos 2α，sin α＋sin 2α)． M 的轨迹的参数方程为{ x ＝cos α＋cos 2α，＝sin α＋sin 2α，(α为参数，0<α<2π)．(2)M 点到坐标原点的距离d ＝x2＋y2＝2＋2cos α(0<α<2π)．当α＝π，d ＝0，故M 的轨迹过坐标原点． 14、已知点A 的极坐标为(2,)4π，直线l 的极坐标方程为cos()4a πρθ-=，且点A 在直线l 上．（1）求a 的值及直线l 的直角坐标方程； （2）圆c 的参数方程为1cos sin x y αα=+⎧⎨=⎩，（α为参数），试判断直线l 与圆的位置关系．2=，15．（2012辽宁）在直角坐标-3）(-3≤≤3) 16．(2013新标1) 已知曲线⎝⎛⎭⎫2，π4⎭⎫，π217．（2013辽宁）⎭⎪⎫－422. ＝2t3解⎨⎪⎧x2＋－＝4，得⎨⎪⎧x1＝0，⎨⎪⎧x2＝2，所以C 与C 交点的一个极坐标为 ⎛⎪⎫4，π，＝12|OA ⎭⎫－π3⎪⎪⎭⎫－π3－32＋ 3. ＝－π12时，＋ 3.＋ 3.23．(2017·全国Ⅲ文，22)在直角坐标系＝m k －2＝＝1k (设P (x ，y )，由题设得⎩⎪⎨⎪⎧y ＝－，y ＝1k＋消去k 得x －y ＝4(y ≠0)．所以C 的普通方程为x －y ＝4(y ≠0)．(2)C 的极坐标方程为ρ2(cos 2θ－sin 2θ)＝4(0＜θ＜2π，θ≠π)．联立⎩⎨⎧－＝4，＋－2＝0，得＝－13，从而＝910，＝110.的极径为 5.24．(2017·江苏，21)在平面直角坐标系中＝t222s22s 从而点P 到直线的距离d ＝|2s2－42s ＋8|5＝－2＋4|，当s ＝2时，d ＝45.。
20122017年高考文科数学真题汇编基本初等函数老师版
11、（2016年山东）已知函数f(x )的定义域为R.当x ＜0时，f(x )=x 3-1；当-1≤x ≤1时，f(-x )= —f(x )；当x ＞12时，f(x +12)=f(x —12).则f(6)=（ D ） （A ）-2 （B ）-1 （C ）0 （D ）212、（2016年天津）已知)(x f 是定义在R 上的偶函数，且在区间)0,(-∞上单调递增，若实数a 满足)2()2(|1|->-f f a ，则a 的取值范围是（ C ）（A ）)21,(-∞（B ）),23()21,(+∞-∞Y （C ）)23,21( （D ）),23(+∞13、（2016年全国I 卷）若a>b>0，0<c<1，则（ B ）（A ）log a c <log b c （B ）log c a <log c b （C ）a c <b c （D ）c a >c b 14、（2016年全国I 卷高考）函数y =2x 2–e |x |在[–2,2]的图像大致为（ D ）（A ）（B ）（C ）（D ）15、（2016年全国II 卷）下列函数中，其定义域和值域分别与函数y=10lg x 的定义域和值域相同的是（ D ）（A ）y =x （B ）y =lg x （C ）y =2x （D ）1y x=16、（2016年全国III 卷）已知4213332,3,25a b c ===，则（ A ）(A) b a c << (B)a b c <<(C) b c a << (D) c a b <<17、（2016年江苏）函数y =232x x --的定义域是 []3,1- .18、（2016年江苏）设f （x ）是定义在R 上且周期为2的函数，在区间[ −1,1)上，,10,()2,01,5x a x f x x x +-≤<⎧⎪=⎨-≤<⎪⎩其中.a ∈R 若59()()22f f -= ，则(5)f a 的值是 25- . 19、（2016年四川高考）若函数f （x ）是定义R 上的周期为2的奇函数，当0<x<1时，f （x ）=x 4，则f （25-）+f （2）= -2 。
2012-2017年高考文科数学真题汇编：基本初等函数老师版
11、（2016年山东)已知函数f(x ）的定义域为R.当x ＜0时,f(x ）=x 3—1；当-1≤x ≤1时,f(-x ）= —f(x )；当x ＞12时，f （x +12）=f(x —12)。
则f （6）=( D ) （A ）—2 (B ）-1 （C)0 （D ）212、（2016年天津）已知)(x f 是定义在R 上的偶函数，且在区间)0,(-∞上单调递增，若实数a 满足)2()2(|1|->-f f a ，则a 的取值范围是（ C ）（A ）)21,(-∞（B)),23()21,(+∞-∞(C ）)23,21(（D ）),23(+∞13、(2016年全国I 卷）若a 〉b>0，0〈c<1，则（ B ）(A ）log a c <log b c (B ）log c a <log c b （C)a c 〈b c （D ）c a >c b 14、（2016年全国I 卷高考)函数y =2x 2–e ｜x |在［–2,2］的图像大致为（ D ）(A ）(B ）(C ）（D)15、（2016年全国II 卷）下列函数中，其定义域和值域分别与函数y=10lg x 的定义域和值域相同的是（ D ）（A ）y =x （B ）y =lg x （C ）y =2x （D ）1y x=16、（2016年全国III 卷）已知4213332,3,25a b c ===，则( A ）（A) b a c << （B ）a b c <<(C) b c a << (D) c a b <<17、(2016年江苏）函数y =232x x --的定义域是 []3,1- 。
18、（2016年江苏）设f (x ）是定义在R 上且周期为2的函数，在区间[ −1，1)上，,10,()2,01,5x a x f x x x +-≤<⎧⎪=⎨-≤<⎪⎩其中.a ∈R 若59()()22f f -= ,则(5)f a 的值是 25- 。
2012-2017年全国高考文科导数大题官方解答
2012--2017全国卷高考真题导数大题1．〔2012新课标全国卷1文21，本小题总分值12分〕设函数()2xf x e ax =--． 〔Ⅰ〕求()f x 的单调区间；〔Ⅱ〕假设1a =，k 为整数，且当0x >时，()()10x k f x x '-++>，求k 的最大值． 解：〔Ⅰ〕()f x 定义域为(,)-∞+∞，()xf x e a '=-，假设0a ≤，则()0f x '>，所以()f x 在(,)-∞+∞单调递增；假设0a >，则当(,ln )x a ∈-∞时，()0f x '<；当(ln ,)x a ∈+∞时，)0f x '>（， 所以()f x 在(,ln )a -∞，单调递减，在(ln ,)a +∞单调递增； 〔Ⅱ〕由于1a =，所以()()1()(1)1xx k f x x x k e x '-++=--++， 故当0x >时，()()10x k f x x '-++>等价于1(0)1x x k x x e +<+>-，① 令1()1x x g x x e +=+-，则221(2)()1(1)(1)x x x xx xe e e x g x e e ----'=+=--， 由〔Ⅰ〕知，函数()2xh x e x =--在(0,)+∞单调递增，而(1)0h <，(2)0h >， 所以()h x 在(0,)+∞存在唯一零点，故()g x '在(0,)+∞存在唯一零点， 设此零点为α，则(1,2)α∈，当(0,)x α∈时，()0g x '<；当(,)x α∈+∞时，)0g x '>（， 所以()g x 在(0,)+∞的最小值是()g α，又()0g α'=，可得2e αα=+，所以()1(2,3)g αα=+∈， 由于①等价于()k g α<，故整数k 的最大值为2．2．〔2013新课标全国卷1文21，本小题总分值12分〕已知函数2()()4xf x e ax b x x =+--，曲线()y f x =在点(0,(0))f 处切线方程为44y x =+．〔Ⅰ〕求,a b 的值；〔Ⅱ〕讨论()f x 的单调性，并求()f x 的极大值． 解：〔Ⅰ〕2()()24f x e ax a b x '=++--，由此得(0)4f =，1(0)4f =，故4b =，8a b += 从而4a =，4b =；〔Ⅱ〕由〔Ⅰ〕知，2)4(1)4x f x e x x x =+--（， 1()4(2)244(2)().2x x f x e x x x e '=+--=+-令()0f x '=得，ln 2x =或2x =-， 从而当(,2)(ln 2,)x ∈-∞--+∞时，()0f x '>；当(2,ln 2)x ∈--时，)0f x '<（， 故()f x 在(,2)-∞-，(ln 2,)-+∞单调递增，在(2,ln 2)--单调递减， 当2x =-时，函数()f x 取得极大值，极大值是2(2)4(1)f e --=-． 3．〔2013新课标Ⅱ卷文21，本小题总分值12分〕己知函数2()xf x x e -=． 〔Ⅰ〕求()f x 的极小值和极大值；〔Ⅱ〕当曲线()y f x =的切线l 的斜率为负数时，求l 在x 轴上截距的取值范围． 解：〔Ⅰ〕()f x 定义域是(,)-∞+∞，()(2)xf x e x x -'=--，①当(,0)x ∈-∞或(2,)x ∈+∞时，)0f x '<（；当(0,2)x ∈时，()0f x '>， 所以故()f x 在(,0)-∞，(2,)+∞单调递减，在(0,2)单调递增， 故当0x =时，()f x 取得极小值，极小值是(0)0f =， 当2x =时，()f x 取得极大值，极大值是2(2)2f e -=， 〔Ⅱ〕设切点是(,())t f t ，则l 的方程是()()()y f t x t f t '=-+，所以l 在x 轴上截距是()2()23()22f t t m t t t t f t t t =-=+=-++'--， 由已知和①得，(,0)t ∈-∞(2,)+∞，令2()h x x x=+，则当(0,)x ∈+∞时，()h x 的取值范围为)+∞， 当(,2)x ∈-∞-时，()h x 的取值范围为(,3)-∞-， 所以(,0)t ∈-∞(2,)+∞时，()m t 的取值范围为(,3)-∞-[22,)+∞，综上，l 在x 轴上截距的取值范围(,3)-∞-[22,)+∞．4．〔2014新课标全国卷1文21，本小题总分值12分〕设函数21()ln (1)2a f x a x x bx a -=+-≠，曲线()y f x =在点(1,(1))f 处的切线斜率为0．〔Ⅰ〕求b ；〔Ⅱ〕假设存在01x ≥，使得0()1af x a <-，求a 的取值范围． 解：〔Ⅰ〕'()(1)af x a x b x=+--，由题设知(1)0f '=，解得1b =． 〔Ⅱ〕()f x 的定义域为(0,)+∞，由〔Ⅰ〕知，21()ln 2a f x a x x x -=+-，1()(1)1()(1)1a a af x a x x x x x a-'=+--=---〔Ⅰ〕假设12a ≤，则11aa≤-，当(1,)x ∈+∞时，()0f x '>，()f x 在(1,)+∞单调递增，所以，存在01x ≥，使得0()1a f x a <-的充要条件为(1)1af a <-，即1121a aa --<-，解得11a <<． 〔Ⅱ〕假设112a <<，则11a a >-，故当(1,)1ax a ∈-时，()0f x '<； 当(,)1a x a ∈+∞-时，()0f x '>，()f x 在(1,)1a a -单调递减，在(,)1a a+∞-单调递增． 所以，存在01x ≥，使得0()1a f x a <-的充要条件为()11a af a a <--，而2()ln 112(1)11a a a a af a a a a a a =++>-----，所以不合题意．〔ⅡⅠ〕假设1a >，则11(1)1221a a af a ---=-=<-．综上，a 的取值范围是(1)(1,)+∞．5．〔2014新课标Ⅱ卷文21，本小题总分值12分〕已知函数32()32f x x x ax =-++，曲线()y f x =在点(0,2)处的切线与x 轴交点的横坐标为2-．〔Ⅰ〕求a ；〔Ⅱ〕证明：当1k <时，曲线()y f x =与直线2y kx =-只有一个交点． 解：〔Ⅰ〕26()3f x x x a =-'+，(0)f a '=，曲线()y f x =在点(0,2)处的切线方程为2y ax =+ 由题设22a-=-，所以1a =． 〔Ⅱ〕由〔Ⅰ〕知，1a =，故32()32f x x x x =-++ 设32()()23(1)4g x f x kx x x k x =-+=-+-+， 由题设知10k ->，当0x ≤时，2()26(1)0g x x x k '=-+->，()g x 单调递增，(1)10g k -=-<，(0)40g =>，所以()0g x =在(,0]-∞有唯一实根，当0x >时，因为(1)0k x ->，所以32()34g x x x >-+， 令32()34h x x x =-+，()3(2)h x x x '=-，()h x 在(0,2)单调递减，在(2,)+∞单调递增，所以()()(2)0g x h x h >≥=， 所以()0g x =在(0,)+∞没有实根，综上()0g x =在R 有唯一实根，即曲线()y f x =与直线2y kx =-只有一个交点．6. 〔2015新课标全国卷1文21，本小题总分值12分〕设函数()2ln xf x ea x =-.〔1〕讨论()f x 的导函数()f x '的零点的个数； 〔2〕证明：当0a >时()22lnf x a a a≥+. 解：〔I 〕()f x 的定义域为0+，，2()=20xaf x e x x. 当0a 时,()0f x ，()f x 没有零点； 当0a 时，因为2x e 单调递增，ax单调递增，所以()f x 在0+，()0f a ,当b满足04a b且14b 时，(b)0f ,故当0a 时，()f x 存在唯一零点. 〔II 〕由〔I 〕，可设()f x 在0+，的唯一零点为0x ，当00xx ，时，()0f x ;当0+xx ，时，()0f x .故()f x 在00x ，单调递减，在0+x ，单调递增，所以当0xx 时，()f x 取得最小值，最小值为0()f x . 由于0202=0x a ex ，所以00022()=2ln2ln2af x ax a a a x aa. 故当0a时，2()2ln f x a a a.考点：常见函数导数及导数运算法则；函数的零点；利用导数研究函数图像与性质；利用导数证明不等式；运算求解能力.7. 〔2016新课标全国卷1文21，本小题总分值12分〕已知函数.2)1()2()(-+-=x a e x x f x(I)讨论)(x f 的单调性； (II)假设)(x f 有两个零点，求a 的取值范围. 【答案】〔Ⅰ〕见解析〔Ⅱ〕()0,+∞解：〔Ⅰ〕()()()()()'12112.x x f x x e a x x e a =-+-=-+〔i 〕设0a ≥，则当(),1x ∈-∞时，()'0f x <；当()1,x ∈+∞时，()'0f x >. 所以在(),1-∞单调递减，在()1,+∞单调递增. 〔ii 〕设0a <，由()'0f x =得x=1或x=ln 〔-2a 〕. ①假设2ea =-，则()()()'1x f x x e e =--，所以()f x 在(),-∞+∞单调递增.②假设2ea >-，则ln 〔-2a 〕＜1,故当()()(),ln 21,x a ∈-∞-+∞时，()'0f x >；当()()ln 2,1x a ∈-时，()'0f x <，所以()f x 在()()(),ln 2,1,a -∞-+∞单调递增，在()()ln 2,1a -单调递减.③假设2ea <-，则()21ln a ->，故当()()(),1ln 2,x a ∈-∞-+∞时，()'0f x >，当()()1,ln 2x a ∈-时，()'0f x <，所以()f x 在()()(),1,ln 2,a -∞-+∞单调递增，在()()1,ln 2a -单调递减.〔Ⅱ〕〔i 〕设0a >，则由〔I 〕知，()f x 在(),1-∞单调递减，在()1,+∞单调递增. 又()()12f e f a =-=，，取b 满足b ＜0且ln 22b a<， 则()()()23321022a f b b a b a b b ⎛⎫>-+-=->⎪⎝⎭，所以()f x 有两个零点. 〔ii 〕设a=0，则()()2xf x x e =-所以()f x 有一个零点.〔iii 〕设a ＜0，假设2ea ≥-，则由〔I 〕知，()f x 在()1,+∞单调递增. 又当1x ≤时，()f x ＜0，故()f x 不存在两个零点；假设2ea <-，则由〔I 〕知，()f x 在()()1,ln 2a -单调递减，在()()ln 2,a -+∞1x ≤时()f x ＜0，故()f x 不存在两个零点.综上，a 的取值范围为()0,+∞.8. 〔2017新课标全国卷1文21，本小题总分值12分〕已知函数()f x =e x (e x ﹣a )﹣a 2x ．〔1〕讨论()f x 的单调性；〔2〕假设()0f x ≥，求a 的取值范围． 解：〔12分〕〔1〕函数()f x 的定义域为(,)-∞+∞，22()2(2)()x x x x f x e ae a e a e a '=--=+-，①假设0a =，则2()xf x e =，在(,)-∞+∞单调递增. ②假设0a >，则由()0f x '=得ln x a =.当(,ln )x a ∈-∞时，()0f x '<；当(ln ,)x a ∈+∞时，()0f x '>，所以()f x 在(,ln )a -∞单调递减，在(ln ,)a +∞单调递增.③假设0a <，则由()0f x '=得ln()2a x =-.当(,ln())2a x ∈-∞-时，()0f x '<；当(ln(),)2a x ∈-+∞时，()0f x '>，故()f x 在(,ln())2a -∞-单调递减，在(ln(),)2a-+∞单调递增.〔2〕①假设0a =，则2()xf x e =，所以()0f x ≥.②假设0a >，则由〔1〕得，当ln x a =时，()f x 取得最小值，最小值为2(ln )ln f a a a =-.从而当且仅当2ln 0a a -≥，即1a ≤时，()0f x ≥.③假设0a <，则由〔1〕得，当ln()2ax =-时，()f x 取得最小值，最小值为23(ln())[ln()]242a a f a -=--.从而当且仅当23[ln()]042aa --≥，即342e a ≥-时()0f x ≥. 综上，a 的取值范围为34[2e ,1]-.。
17年高考真题—文科数学2：导数
2017高考真题分类汇编：导数1．【2017浙江 7】函数()y f x =的导函数()y f x '=的图像如图所示，则函数()y f x =的图像可能是（ ）2．【2017天津 10】已知a R ∈，设函数()ln f x ax x =-的图象在点()()1,1f 处的切线为l ，则l 在y 轴上的截距为__________。
3．【2017课标I 14】曲线21y x x=+在点()1,2处的切线方程为__________________。
4．【2017天津 19】设,a b R ∈，||1a ≤。
已知函数()()32634f x x x a a x b =---+，()()xg x e f x =。
⑴求()f x 的单调区间；⑵已知函数()y g x =和x y e =的图象在公共点()00,x y 处有相同的切线，①求证：()f x 在0x x =处的导数等于0；②若关于x 的不等式()x g x e ≤在区间[]001,1x x -+上恒成立，求b 的取值范围。
5．【2017北京 20】已知函数()cos xf x e x x =-。
⑴求曲线()y f x =在点()()0,0f 处的切线方程；⑵求函数()f x 在区间[]0,2π上的最大值和最小值。
6．【2017江苏 20】已知函数()()3210,f x x ax bx a b R =+++>∈有极值，且导函数()f x '的极值点是()f x 的零点（极值点是指函数取极值时对应的自变量的值）。
⑴求b 关于a 的函数关系式，并写出定义域；⑵证明：23b a >；⑶若()(),f x f x '这两个函数的所有极值之和不小于72-，求a 的取值范围。
7．【2017山东 20】已知函数()()321132f x x ax a R =-∈。
⑴当2a =时，求曲线()y f x =在点()()3,3f 处的切线方程；⑵设函数()()()cos sin g x f x x a x x =+--，讨论()g x 的单调性并判断有无极值，有极值时求出极值。
2012-2017年高考文科数学真题总汇编：圆锥曲线老师版
（Ⅱ）因为AB 过点(1,0)D 且垂直于x 轴，所以可设1(1,)A y ，1(1,)B y -. 直线AE 的方程为11(1)(2)y y x -=--.令3x =，得1(3,2)M y -. 所以直线BM 的斜率112131BM y y k -+==-.17.（2015年文）设椭圆E 的方程为22221(0),x y a b a b+=>>点O 为坐标原点，点A 的坐标为(,0)a ,点B的坐标为（0，b ）,点M 在线段AB 上，满足2,BM MA =直线OM 的斜率为510。
[学优高考网]（1）求E 的离心率e;(2)设点C 的坐标为（0，-b ）,N 为线段AC 的中点，证明：MN ⊥AB 。
∴a b3231＝5525451511052222222=⇒=⇒=-⇒=⇒e a c a c a a b（Ⅱ）由题意可知N 点的坐标为（2,2b a -）∴a b a ba a bb K MN 56652322131==-+= abK AB-=∴1522-=-=⋅a b K K AB MN ∴MN ⊥AB18.（2015年文）已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为F ．短轴的一个端点为M ，直线:340l x y -=交椭圆E 于,A B 两点．若4AF BF +=，点M 到直线l 的距离不小于45，则椭圆E 的离心率的取值围是（ A ） A ． 3(0,]2 B ．3(0,]4 C ．3[,1)2 D ．3[,1)4119.（2015年新课标2文）已知双曲线过点()4,3,且渐近线方程为12y x =±,则该双曲线的标准方程为 ．2214x y -= 20.（2015年文）已知抛物线22(0)y px p =>的准线经过点(1,1)-，则抛物线焦点坐标为（ B ） A ．(1,0)- B ．(1,0) C ．(0,1)- D ．(0,1) 【解析】试题分析：由抛物线22(0)y px p =>得准线2px =-，因为准线经过点(1,1)-，所以2p =， 所以抛物线焦点坐标为(1,0)，故答案选B 考点：抛物线方程.21.（2015年文科）如图，椭圆2222:1(0)x y E a b a b+=>>经过点(0,1)A -，且离心率为22.(I)求椭圆E 的方程；2212x y += 22.（2015年文）已知双曲线22221(0,0)x y a b ab 的一个焦点为(2,0)F ,且双曲线的渐近线与圆222y 3x 相切,则双曲线的方程为（ D ）(A)221913x y (B) 221139x y (C)2213x y(D) 2213y x2b上，则双曲线的方程为（A）202215x y（C）325100D）223310025x y新标1) 已知双曲线21=（0,a b>>）的离心率为52，则C．(0,1][4,)+∞D．(0,3][4,)+∞【答案】A【解析】当03m<<，焦点在x轴上，要使C上存在点M满足120AMB∠=，则tan603ab≥=，即33m≥，得01m<≤；当3m>，焦点在y轴上，要使C上存在点M满足120AMB∠=，则tan603ab≥=，即33m≥，得9m≥，故m的取值围为(0,1][9,)⋃+∞，选A.41、(2017·全国Ⅱ文，5)若a>1，则双曲线x2a2－y2＝1的离心率的取值围是()A．(2，＋∞) B．(2，2) C．(1，2) D．(1,2)3．【答案】C【解析】由题意得双曲线的离心率e＝a2＋1a.∴e2＝a2＋1a2＝1＋1a2.∵a＞1，∴0＜1a2＜1，∴1＜1＋1a2＜2，∴1＜e＜ 2.故选C.42．(2017·全国Ⅱ文，12)过抛物线C：y2＝4x的焦点F，且斜率为3的直线交C于点M(M在x轴上方)，l为C的准线，点N在l上且MN⊥l，则M到直线NF的距离为()A. 5 B．2 2 C．2 3 D．3 34．【答案】C【解析】抛物线y2＝4x的焦点为F(1,0)，准线方程为x＝－1.由直线方程的点斜式可得直线MF的方程为y＝3(x－1)．联立得方程组⎩⎪⎨⎪⎧y＝3(x－1)，y2＝4x，解得⎩⎨⎧x＝13，y＝－233或⎩⎨⎧x＝3，y＝2 3.∵点M在x轴的上方，∴M(3,23)．∵MN⊥l，∴N(－1,23)．∴|NF|＝(1＋1)2＋(0－23)2＝4，|MF|＝|MN|＝3－(－1)＝4.∴△MNF是边长为4的等边三角形．∴点M到直线NF的距离为2 3.故选C.43．(2017·全国Ⅲ文，11)已知椭圆C：x2a2＋y2b2＝1(a>b>0)的左、右顶点分别为A1，A2，且以线段A1A2为直径的圆与直线bx－ay＋2ab＝0相切，则椭圆C的离心率为()A．63B．33C．23D．135．【答案】A【解析】由题意知以A1A2为直径的圆的圆心坐标为(0,0)，半径为a.又直线bx －ay ＋2ab ＝0与圆相切，∴圆心到直线的距离d ＝2aba 2＋b 2＝a ，解得a ＝3b ， ∴b a ＝13，∴e ＝ca ＝a 2－b 2a ＝ 1－⎝⎛⎭⎫b a 2＝1－⎝⎛⎭⎫132＝63. 44．(2017·文，5)已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的右焦点为F ，点A 在双曲线的渐近线上，△OAF 是边长为2的等边三角形(O 为原点)，则双曲线的方程为( ) A ．x 24－y 212＝1B ．x 212－y 24＝1C ．x 23－y 2＝1D ．x 2－y 23＝1 6．【答案】D 【解析】根据题意画出草图如图所示⎝⎛⎭⎫不妨设点A 在渐近线y ＝ba x 上.由△AOF 是边长为2的等边三角形得到∠AOF ＝60°，c ＝|OF |＝2.又点A 在双曲线的渐近线y ＝b a x 上，∴ba ＝tan 60°＝ 3.又a 2＋b 2＝4，∴a ＝1，b ＝3，∴双曲线的方程为x 2－y 23＝1.故选D. 45．(2017·全国Ⅲ文，14)双曲线x 2a 2－y 29＝1(a >0)的一条渐近线方程为y ＝35x ，则a ＝________.1．【答案】5【解析】∵双曲线的标准方程为x 2a 2－y 29＝1(a ＞0)，∴双曲线的渐近线方程为y ＝±3a x .又双曲线的一条渐近线方程为y ＝35x ，∴a ＝5.46、(2017·文，10)若双曲线x 2－y 2m＝1的离心率为3，则实数m ＝________. 【答案】2【解析】由双曲线的标准方程知a ＝1，b 2＝m ，c ＝1＋m ，故双曲线的离心率e ＝ca ＝1＋m ＝3，∴1＋m ＝3，∴m ＝2.47、(2017·全国Ⅱ理，16)已知F 是抛物线C ：y 2＝8x 的焦点，M 是C 上一点，FM 的延长线交y 轴于点N .若M 为FN 的中点，则|FN |＝________.【解析】如图，不妨设点M 位于第一象限，抛物线C 的准线交x 轴于点A ，过点M 作准线的垂线，垂足为点B ，交y 轴于点P ，∴PM ∥OF .12442222x x x x ==----()12200x x ++= 又设AB ：y=x ＋m 代入x ＋20=0∴m=7故AB ：x ＋y=7。
2012-2017年高考文科数学真题总汇编：圆锥曲线老师版
∴a b3231＝5525451511052222222=⇒=⇒=-⇒=⇒e a c a c a a b（Ⅱ）由题意可知N 点的坐标为（2,2b a -）∴a b a ba a bb K MN 56652322131==-+= abK AB-=∴1522-=-=⋅a b K K AB MN ∴MN ⊥AB 18.（2015年福建文）已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为F ．短轴的一个端点为M ，直线:340l x y -=交椭圆E 于,A B 两点．若4AF BF +=，点M 到直线l 的距离不小于45，则椭圆E 的离心率的取值范围是（ A ） A ． 3(0,]2 B ．3(0,]4 C ．3[,1)2 D ．3[,1)4119.（2015年新课标2文）已知双曲线过点()4,3,且渐近线方程为12y x =±,则该双曲线的标准方程为 ．2214x y -= 20.（2015年陕西文）已知抛物线22(0)y px p =>的准线经过点(1,1)-，则抛物线焦点坐标为（ B ）A ．(1,0)-B ．(1,0)C ．(0,1)-D ．(0,1)【解析】试题分析：由抛物线22(0)y px p =>得准线2px =-，因为准线经过点(1,1)-，所以2p =， 所以抛物线焦点坐标为(1,0)，故答案选B 考点：抛物线方程.21.（2015年陕西文科）如图，椭圆2222:1(0)x y E a b a b+=>>经过点(0,1)A -，且离心率为22.(I)求椭圆E 的方程；2212x y += 22.（2015年天津文）已知双曲线22221(0,0)x y a b a b-=>>的一个焦点为(2,0)F ,且双曲线的渐近线与圆()222y 3x -+=相切,则双曲线的方程为（ D ）(A)221913x y -= (B) 221139x y -= (C) 2213x y -= (D) 2213y x -= 23．（2013广东文）已知中心在原点的椭圆C 的右焦点为(1,0)F ，离心率等于21，则C 的方程是（ D ） A ．14322=+y x B ．13422=+y x C ．12422=+y x D ．13422=+y x24．(2012沪春招) 已知椭圆222212:1,:1,124168x y x y C C +=+=则 （ D ） (A)1C 与2C 顶点相同. （B ）1C 与2C 长轴长相同. (C)1C 与2C 短轴长相同. （D ）1C 与2C 焦距相等.25.(2012新标) 设12F F 是椭圆2222:1(0)x y E a b a b +=>>的左、右焦点，P 为直线32ax =上一点，∆21F PF 是底角为30o 的等腰三角形，则E 的离心率为（ C ）()A 12 ()B 23 ()C 34()D 4526.(2013新标2文) 设椭圆C ：x 2a2＋y 2b 2＝1(a >b >0)的左、右焦点分别为F 1、F 2，P 是C 上的点，PF 2⊥F 1F 2，∠PF 1F 2＝30°，则C 的离心率为( D ) A.36B.13C.12D.3327.(2013四川文) 从椭圆x 2a 2＋y 2b 2＝1(a >b >0)上一点P 向x 轴作垂线，垂足恰为左焦点F 1，A 是椭圆与x轴正半轴的交点，B 是椭圆与y 轴正半轴的交点，且AB ∥OP (O 是坐标原点)，则该椭圆的离心率是( ) A.24 B.12 C.22 D.32【简解】由题意可设P (－c ，y 0)(c 为半焦距)，k OP ＝－y 0c，k AB ＝－b a，由于OP ∥AB ，∴－y 0c＝－b a，y 0＝bc a，把P ⎝⎛⎭⎪⎫－c ，bc a 代入椭圆方程得－c 2a 2＋⎝ ⎛⎭⎪⎫bc a 2b 2＝1，而⎝ ⎛⎭⎪⎫c a 2＝12，∴e ＝c a ＝22.选C.28．（2014大纲）已知椭圆C ：22221x y a b+=(0)a b >>的左、右焦点为1F 、2F ，离心率为33，过2F 的直线l 交C 于A 、B 两点，若1AF B ∆的周长为43，则C 的方程为（ ）A ．22132x y += B ．2213x y += C ．221128x y += D ．221124x y +=【答案】D 【解析】由2224c a b =+=得2c =，所以(2,0)F ，将2x =代入2213y x -=，得3y =±，所以3PF =，又A 的坐标是(1,3)，故APF 的面积为133(21)22⨯⨯-=，选D.40.(2017新课标1文)设A 、B 是椭圆C ：2213x y m+=长轴的两个端点，若C 上存在点M 满足∠AMB =120°，则m 的取值范围是 （ A ） A ．(0,1][9,)+∞U B ．(0,3][9,)+∞U C ．(0,1][4,)+∞UD ．(0,3][4,)+∞U【答案】A 【解析】当03m <<，焦点在x 轴上，要使C 上存在点M 满足120AMB ∠=o，则tan 603ab≥=o ，即33m≥，得01m <≤；当3m >，焦点在y 轴上，要使C 上存在点M 满足120AMB ∠=o ，则tan 603a b ≥=o ，即33m ≥，得9m ≥，故m 的取值范围为(0,1][9,)⋃+∞，选A. 41、(2017·全国Ⅱ文，5)若a >1，则双曲线x 2a2－y 2＝1的离心率的取值范围是( )A ．(2，＋∞)B ．(2，2)C ．(1，2)D ．(1,2) 3．【答案】C 【解析】由题意得双曲线的离心率e ＝a 2＋1a.∴e 2＝a 2＋1a 2＝1＋1a2.∵a ＞1，∴0＜1a 2＜1，∴1＜1＋1a2＜2，∴1＜e ＜2.故选C.42．(2017·全国Ⅱ文，12)过抛物线C ：y 2＝4x 的焦点F ，且斜率为3的直线交C 于点M (M 在x 轴上方)，l 为C 的准线，点N 在l 上且MN ⊥l ，则M 到直线NF 的距离为( )A. 5 B ．2 2 C ．2 3 D ．3 34．【答案】C 【解析】抛物线y 2＝4x 的焦点为F (1,0)，准线方程为x ＝－1.由直线方程的点斜式可得直线MF 的方程为y ＝3(x －1)．联立得方程组⎩⎪⎨⎪⎧y ＝3x －1，y 2＝4x ，解得⎩⎪⎨⎪⎧x ＝13，y ＝－233或⎩⎪⎨⎪⎧x ＝3，y ＝2 3.∵点M 在x 轴的上方，∴M (3,23)．∵MN ⊥l ，∴N (－1,23)．∴|NF |＝1＋12＋0－232＝4，|MF |＝|MN |＝3－(－1)＝4.∴△MNF 是边长为4的等边三角形．∴点M 到直线NF 的距离为2 3.故选C.43．(2017·全国Ⅲ文，11)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右顶点分别为A 1，A 2，且以线段A 1A 2为直径的圆与直线bx －ay ＋2ab ＝0相切，则椭圆C 的离心率为( ) A ．63 B ．33 C ．23 D ．135．【答案】A 【解析】由题意知以A 1A 2为直径的圆的圆心坐标为(0,0)，半径为a . 又直线bx －ay ＋2ab ＝0与圆相切，∴圆心到直线的距离d ＝2aba 2＋b 2＝a ，解得a ＝3b ，∴b a＝13，∴e ＝c a ＝a 2－b 2a＝1－⎝ ⎛⎭⎪⎫b a 2＝1－⎝ ⎛⎭⎪⎪⎫132＝63. 44．(2017·天津文，5)已知双曲线x 2a2－y 2b 2＝1(a >0，b >0)的右焦点为F ，点A 在双曲线的渐近线上，△OAF是边长为2的等边三角形(O 为原点)，则双曲线的方程为( ) A ．x 24－y 212＝1B ．x 212－y 24＝1C ．x 23－y 2＝1D ．x 2－y 23＝16．【答案】D 【解析】根据题意画出草图如图所示⎝⎛⎭⎪⎫不妨设点A 在渐近线y ＝b a x 上.由△AOF 是边长为2的等边三角形得到∠AOF ＝60°，c ＝|OF |＝2.又点A 在双曲线的渐近线y ＝b a x 上，∴ba＝tan 60°＝3.又a 2＋b 2＝4，∴a ＝1，b ＝3，∴双曲线的方程为x 2－y 23＝1.故选D.45．(2017·全国Ⅲ文，14)双曲线x 2a 2－y 29＝1(a >0)的一条渐近线方程为y ＝35x ，则a ＝________.1．【答案】5【解析】∵双曲线的标准方程为x 2a 2－y 29＝1(a ＞0)，∴双曲线的渐近线方程为y ＝±3a x .又双曲线的一条渐近线方程为y ＝35x ，∴a ＝5.46、(2017·北京文，10)若双曲线x 2－y 2m＝1的离心率为3，则实数m ＝________.【答案】2【解析】由双曲线的标准方程知a ＝1，b 2＝m ，c ＝1＋m ，故双曲线的离心率e ＝ca＝1＋m＝3，∴1＋m ＝3，∴m ＝2.47、(2017·全国Ⅱ理，16)已知F 是抛物线C ：y 2＝8x 的焦点，M 是C 上一点，FM 的延长线交y 轴于点N .若M 为FN 的中点，则|FN |＝________.【解析】如图，不妨设点M 位于第一象限内，抛物线C 的准线交x 轴于点A ，过点M 作准线的垂线，垂足为点B ，交y 轴于点P ，∴PM ∥OF .由题意知，F (2,0)，|FO |＝|AO |＝2.∵点M 为FN 的中点，PM ∥OF ，∴|MP |＝12|FO |＝1.又|BP |＝|AO |＝2，∴|MB |＝|MP |＋|BP |＝3.由抛物线的定义知|MF |＝|MB |＝3，故|FN |＝2|MF |＝6.48、(2017新课标1文)设A ，B 为曲线C ：y =24x 上两点，A 与B 的横坐标之和为4. （1）求直线AB 的斜率；（2）设M 为曲线C 上一点，C 在M 处的切线与直线AB 平行，且AM ⊥BM ，求直线AB 的方程. 【解析】（1）设()()1122,,,A x y B x y ，则2221212121214414AB x x y y x x K x x x x --+====-- （2）设200,4x M x ⎛⎫ ⎪⎝⎭ ，则C 在M 处的切线斜率'00112ABy K K x x x ====- ∴02x = 则()12,1A ，又AM ⊥BM ，22121212121111442222AM BMx x y y K K x x x x ----==----g g g ()()()121212222411616x x x x x x +++++===-即()12122200x x x x +++= 又设AB ：y=x ＋m 代入24x y = 得2440x x m --= ∴124x x +=，124x x m =- －4m ＋8＋20=0∴m=7故AB ：x ＋y=749.(2017年新课标Ⅱ文)设O 为坐标原点,动点M 在椭圆C :x 22＋y 2＝1上，过M 作x 轴的垂线,垂足为N ,点P 满足→NP ＝2→NM .(1)求点P 的轨迹方程；(2)设点Q 在直线x ＝－3上,且→OP ·→PQ ＝1.证明:过点P 且垂直于OQ 的直线l 过C 的左焦点F . 【解析】(1)设P (x ,y ),M (x 0,y 0),则N (x 0,0),→NP ＝(x －x 0,y ),→NM ＝(0,y 0).由→NP ＝2→NM 得x 0＝x ,y 0＝22y .。
2012-2017年全国高考文科导数大题官方解答
2012--2017全国卷高考真题导数大题1．（2012新课标全国卷1文21，本小题满分12分）设函数()2xf x e ax =--． （Ⅰ）求()f x 的单调区间；（Ⅱ）若1a =，k 为整数，且当0x >时，()()10x k f x x '-++>，求k 的最大值． 解：（Ⅰ）()f x 定义域为(,)-∞+∞，()xf x e a '=-，若0a ≤，则()0f x '>，所以()f x 在(,)-∞+∞单调递增；若0a >，则当(,ln )x a ∈-∞时，()0f x '<；当(ln ,)x a ∈+∞时，)0f x '>（， 所以()f x 在(,ln )a -∞，单调递减，在(ln ,)a +∞单调递增； （Ⅱ）由于1a =，所以()()1()(1)1xx k f x x x k e x '-++=--++， 故当0x >时，()()10x k f x x '-++>等价于1(0)1x x k x x e +<+>-，① 令1()1x x g x x e +=+-，则221(2)()1(1)(1)x x x xx xe e e x g x e e ----'=+=--， 由（Ⅰ）知，函数()2xh x e x =--在(0,)+∞单调递增，而(1)0h <，(2)0h >， 所以()h x 在(0,)+∞存在唯一零点，故()g x '在(0,)+∞存在唯一零点， 设此零点为α，则(1,2)α∈，当(0,)x α∈时，()0g x '<；当(,)x α∈+∞时，)0g x '>（， 所以()g x 在(0,)+∞的最小值是()g α，又()0g α'=，可得2e αα=+，所以()1(2,3)g αα=+∈， 由于①等价于()k g α<，故整数k 的最大值为2．2．（2013新课标全国卷1文21，本小题满分12分）已知函数2()()4xf x e ax b x x =+--，曲线()y f x =在点(0,(0))f 处切线方程为44y x =+．（Ⅰ）求,a b 的值；（Ⅱ）讨论()f x 的单调性，并求()f x 的极大值． 解：（Ⅰ）2()()24f x e ax a b x '=++--，由此得(0)4f =，1(0)4f =，故4b =，8a b += 从而4a =，4b =；（Ⅱ）由（Ⅰ）知，2)4(1)4x f x e x x x =+--（， 1()4(2)244(2)().2x x f x e x x x e '=+--=+-令()0f x '=得，ln 2x =或2x =-，从而当(,2)(ln 2,)x ∈-∞--+∞U 时，()0f x '>；当(2,ln 2)x ∈--时，)0f x '<（， 故()f x 在(,2)-∞-，(ln 2,)-+∞单调递增，在(2,ln 2)--单调递减， 当2x =-时，函数()f x 取得极大值，极大值是2(2)4(1)f e --=-． 3．（2013新课标Ⅱ卷文21，本小题满分12分）己知函数2()xf x x e -=． （Ⅰ）求()f x 的极小值和极大值；（Ⅱ）当曲线()y f x =的切线l 的斜率为负数时，求l 在x 轴上截距的取值范围． 解：（Ⅰ）()f x 定义域是(,)-∞+∞，()(2)xf x e x x -'=--，①当(,0)x ∈-∞或(2,)x ∈+∞时，)0f x '<（；当(0,2)x ∈时，()0f x '>， 所以故()f x 在(,0)-∞，(2,)+∞单调递减，在(0,2)单调递增， 故当0x =时，()f x 取得极小值，极小值是(0)0f =， 当2x =时，()f x 取得极大值，极大值是2(2)2f e -=， （Ⅱ）设切点是(,())t f t ，则l 的方程是()()()y f t x t f t '=-+，所以l 在x 轴上截距是()2()23()22f t t m t t t t f t t t =-=+=-++'--， 由已知和①得，(,0)t ∈-∞U (2,)+∞，令2()h x x x=+，则当(0,)x ∈+∞时，()h x 的取值范围为)+∞， 当(,2)x ∈-∞-时，()h x 的取值范围为(,3)-∞-，所以(,0)t ∈-∞U (2,)+∞时，()m t 的取值范围为(,3)-∞-U )+∞，综上，l 在x 轴上截距的取值范围(,3)-∞-U )+∞． 4．（2014新课标全国卷1文21，本小题满分12分）设函数21()ln (1)2a f x a x x bx a -=+-≠，曲线()y f x =在点(1,(1))f 处的切线斜率为0．（Ⅰ）求b ；（Ⅱ）若存在01x ≥，使得0()1af x a <-，求a 的取值范围． 解：（Ⅰ）'()(1)af x a x b x=+--，由题设知(1)0f '=，解得1b =． （Ⅱ）()f x 的定义域为(0,)+∞，由（Ⅰ）知，21()ln 2a f x a x x x -=+-，1()(1)1()(1)1a a af x a x x x x x a-'=+--=---（Ⅰ）若12a ≤，则11aa≤-，当(1,)x ∈+∞时，()0f x '>，()f x 在(1,)+∞单调递增，所以，存在01x ≥，使得0()1a f x a <-的充要条件为(1)1af a <-，即1121a a a --<-，解得11a <<． （Ⅱ）若112a <<，则11a a >-，故当(1,)1ax a ∈-时，()0f x '<；当(,)1a x a ∈+∞-时，()0f x '>，()f x 在(1,)1a a -单调递减，在(,)1a a+∞-单调递增． 所以，存在01x ≥，使得0()1a f x a <-的充要条件为()11a af a a <--，而2()ln 112(1)11a a a a af a a a a a a =++>-----，所以不合题意． （ⅡⅠ）若1a >，则11(1)1221a a af a ---=-=<-．综上，a 的取值范围是(1)(1,)+∞U ． 5．（2014新课标Ⅱ卷文21，本小题满分12分）已知函数32()32f x x x ax =-++，曲线()y f x =在点(0,2)处的切线与x 轴交点的横坐标为2-．（Ⅰ）求a ；（Ⅱ）证明：当1k <时，曲线()y f x =与直线2y kx =-只有一个交点． 解：（Ⅰ）26()3f x x x a =-'+，(0)f a '=，曲线()y f x =在点(0,2)处的切线方程为2y ax =+ 由题设22a-=-，所以1a =． （Ⅱ）由（Ⅰ）知，1a =，故32()32f x x x x =-++ 设32()()23(1)4g x f x kx x x k x =-+=-+-+， 由题设知10k ->，当0x ≤时，2()26(1)0g x x x k '=-+->，()g x 单调递增，(1)10g k -=-<，(0)40g =>，所以()0g x =在(,0]-∞有唯一实根，当0x >时，因为(1)0k x ->，所以32()34g x x x >-+， 令32()34h x x x =-+，()3(2)h x x x '=-，()h x 在(0,2)单调递减，在(2,)+∞单调递增，所以()()(2)0g x h x h >≥=， 所以()0g x =在(0,)+∞没有实根，综上()0g x =在R 有唯一实根，即曲线()y f x =与直线2y kx =-只有一个交点．6. （2015新课标全国卷1文21，本小题满分12分）设函数()2ln xf x ea x =-.（1）讨论()f x 的导函数()f x '的零点的个数；（2）证明：当0a >时()22lnf x a a a≥+. 解：（I ）()f x 的定义域为()0+¥，，()2()=20xaf x ex x¢->. 当0a £时,()0f x ¢>，()f x ¢没有零点； 当0a >时，因为2x e 单调递增，ax-单调递增，所以()f x ¢在()0+¥，单调递增.又()0f a ¢>,当b 满足04a b <<且14b <时，(b)0f ¢<,故当0a >时，()f x ¢存在唯一零点.（II ）由（I ），可设()f x ¢在()0+¥，的唯一零点为0x ，当()00x x Î，时，()0f x ¢<;当()0+x x 违，时，()0f x ¢>. 故()f x 在()00x ，单调递减，在()0+x ¥，单调递增，所以当0x x=时，()f x 取得最小值，最小值为0()f x . 由于0202=0x a ex -，所以00022()=2ln 2ln 2a f x ax a a a x a a++?. 故当0a >时，2()2lnf x a a a?. 考点：常见函数导数及导数运算法则；函数的零点；利用导数研究函数图像与性质；利用导数证明不等式；运算求解能力.7. （2016新课标全国卷1文21，本小题满分12分）已知函数.2)1()2()(-+-=x a e x x f x(I)讨论)(x f 的单调性； (II)若错误!未找到引用源。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
学科教师辅导教案学员姓名年级高三辅导科目数学授课老师课时数2h 第次课授课日期及时段 2018年月日：—：1．（2014大纲理）曲线1xy xe-=在点（1,1）处切线的斜率等于（ C ）A．2e B．e C．2 D．12.(2014新标2理) 设曲线y=a x-ln(x+1)在点(0,0)处的切线方程为y=2x，则a= （ D ）A. 0B. 1C. 2D. 33.(2013浙江文) 已知函数y＝f(x)的图象是下列四个图象之一，且其导函数y＝f′(x)的图象如右图所示，则该函数的图象是(B)4．（2012陕西文）设函数f（x）=2x+lnx 则（ D ）A．x=12为f(x)的极大值点B．x=12为f(x)的极小值点C．x=2为f(x)的极大值点D．x=2为f(x)的极小值点5.(2014新标2文) 函数()f x在x x=处导数存在，若:()0p f x=：:q x x=是()f x的极值点，则A．p是q的充分必要条件 B. p是q的充分条件，但不是q的必要条件C. p是q的必要条件，但不是q的充分条件D. p既不是q的充分条件，也不是q的必要条件【答案】C6．（2012广东理）曲线33y x x=-+在点()1,3处的切线方程为___________________.【答案】2x-y+1=07．（2013广东理）若曲线lny kx x=+在点(1,)k处的切线平行于x轴，则k=【答案】-18．（2013广东文）若曲线2lny ax x=-在点(1,)a处的切线平行于x轴，则a=．历年高考试题汇编（文）——导数及应用【答案】129．(2014广东文)曲线53x y e =-+在点(0,2)-处的切线方程为 . 【答案】5x+y+2=010．（2013江西文）若曲线y=x α+1（α∈R ）在点（1，2）处的切线经过坐标原点，则α= 。
【答案】211.(2012新标文) 曲线(3ln 1)y x x =+在点（1,1）处的切线方程为____430x y --=____12．（2014江西理）若曲线xy e -=上点P 处的切线平行于直线210x y ++=，则点P 的坐标是________. 【简解】设P(x,e -x )，()x e -'=-xe -=-2,解得x=-ln2，答案(-ln2,2)13．（2014江西文）若曲线P x x y 上点ln =处的切线平行于直线P y x 则点,012=+-的坐标是_______. 【简解】设P(x,xlnx),()ln x x '=1+lnx=2,x=e ，答案(e,e) 14．（2012辽宁文）函数y=12x 2-㏑x 的单调递减区间为（ B ） （A ）（-1,1] （B ）（0,1] （C.）[1，+∞） （D ）（0，+∞）15．(2014新标2文) 若函数()f x kx lnx =-在区间()1,+∞单调递增，则k 的取值范围是（ D ）（A ）(],2-∞- （B ）(],1-∞- （C ）[)2,+∞ （D ）[)1,+∞ 16. (2013新标1文) 函数()(1cos )sin f x x x =-在[,]ππ-的图象大致为（ ）【简解】y '=2sin (1cos )cos x x x +-=-2cos 2x-cosx+1=(1+cosx)(1-2cosx)>0,-π/3<x<π/3；23、（2016年全国III 卷高考）已知()f x 为偶函数，当0x ≤ 时，1()x f x ex --=-，则曲线()y f x =在点(1,2)处的切线方程式______________2y x =_______________.24．（2012福建理）已知函数f (x )＝e x ＋ax 2－e x ，a ∈R ．(1)若曲线y ＝f (x )在点(1，f (1))处的切线平行于x 轴，求函数f (x )的单调区间； 【解析】(1)由于f ′(x )＝e x ＋2ax －e ，曲线y ＝f (x )在点(1，f (1))处切线斜率k ＝2a ＝0，所以a ＝0，即f (x )＝e x －e x ．此时f ′(x )＝e x －e ，由f ′(x )＝0得x ＝1． 当x ∈(－∞，1)时，有f ′(x )＜0；当x ∈(1，＋∞)时，有f ′(x )＞0． 所以f (x )的单调递减区间为(－∞，1)，单调递增区间为(1，＋∞)．25.(2013新标1文) 已知函数2()()4xf x e ax b x x =+--，曲线()y f x =在点(0,(0))f 处切线方程为44y x =+。
（Ⅰ）求,a b 的值；（Ⅱ）讨论()f x 的单调性，并求()f x 的极大值。
【简解】 (1)f′(x)＝e x (ax ＋a ＋b)－2x －4. 由已知得f(0)＝4，f ′(0)＝4，故b ＝4，a ＋b ＝8.从而a ＝4，b ＝4.(2)由(1)知，f(x)＝4e x (x ＋1)－x 2－4x. f ′(x)＝4e x (x ＋2)－2x －4＝4(x ＋2)⎝⎛⎭⎫e x －12. 当x ∈(－∞，－2)∪(－ln 2，＋∞)时，f ′(x)>0；当x ∈(－2，－ln 2)时，f ′(x)<0. 故f(x)在(－∞，－2)，(－ln 2，＋∞)上单调递增，在(－2，－ln 2)上单调递减．当x ＝－2时，函数f(x)取得极大值，极大值为f(－2)＝4(1－e －2)． 26.(2014新标1文) 设函数()()21ln 12a f x a x x bx a -=+-≠，曲线()()()11y f x f =在点，处的切线斜率为0。
求b;⑵若存在01,x ≥使得()01af x a <-，求a 的取值范围。
⑴ 【解析】（I ）'()(1)af x a x b x=+--，由题设知'(1)0f =，解得1b =. （2）函数f （x ）的定义域为（0，+∞），由（1）可知：f （x ）=alnx+，∴=．①当a时，则，则当x ＞1时，f′（x ）＞0，∴函数f （x ）在（1，+∞）单调递增，∴存在x 0≥1，使得f （x 0）＜的充要条件是，即，解得；②当a ＜1时，则，则当x ∈时，f′（x ）＜0，函数f （x ）在上单调递减； 当x ∈时，f′（x ）＞0，函数f （x ）在上单调递增．∴存在x 0≥1，使得f （x 0）＜的充要条件是，而=+，不符合题意，应舍去．③若a ＞1时，f （1）=，成立．综上可得：a 的取值范围是．27.(2013新标2理) 已知函数f (x )＝e x －ln(x ＋m )．(1)设x ＝0是f (x )的极值点，求m ，并讨论f (x )的单调性； (2)当m ≤2时，证明f (x )>0.【解析】(1)f (x )＝e x －ln(x ＋m )⇒f ′(x )＝e x －1x ＋m ⇒f ′(0)＝e 0－10＋m ＝0⇒m ＝1，定义域为{x |x >－1}，f ′(x )＝e x－1x ＋m ＝e x (x ＋1)－1x ＋1，显然f (x )在(－1,0]上单调递减，在[0，＋∞)上单调递增．28．（2013北京文）已知函数2()sin cos f x x x x x =++（1）若曲线()y f x =在点(,())a f a 处与直线y b =相切，求a 与b 的值。
（2）若曲线()y f x =与直线y b =有两个不同的交点，求b 的取值范围。
【解析】（1）'()2cos (2cos )f x x x x x x =+=+，因为曲线()y f x =在点(,())a f a 处的切线为y b =所以'()0()f a f a b =⎧⎨=⎩，即22cos 0sin cos a a a a a a a b+=⎧⎨++=⎩，解得01a b =⎧⎨=⎩（2）因为2cos 0x +>，所以当0x >时'()0f x >，()f x 单调递增；当0x <时'()0f x <，()f x 单调递减， 所以当0x =时，()f x 取得最小值(0)1f =， 所以b 的取值范围是(1,)+∞ 29．（2012山东）已知函数ln ()(exx kf x k +=为常数，e=2.71828…是自然对数的底数)，曲线()y f x =在点(1,(1))f 处的切线与x 轴平行.(Ⅰ)求k 的值； (Ⅱ)求()f x 的单调区间； 【解析】(I)1ln ()e x x kx f x --'=，由已知，1(1)0ek f -'==，∴1k =.(II)由(I)知，1ln 1()e xx x f x --'=.设1()ln 1k x x x =--，则211()0k x x x'=--<，即()k x 在(0,)+∞上是减函数，由(1)0k =知，当01x <<时()0k x >，从而()0f x '>，当1x >时()0k x <，从而()0f x '<. 综上可知，()f x 的单调递增区间是(0,1)，单调递减区间是(1,)+∞.30.(2017·天津文，10)已知a ∈R ，设函数f (x )＝ax －ln x 的图象在点(1，f (1))处的切线为l ，则l 在y 轴上的截距为_____1___．31.（2015年新课标2文）已知()()ln 1f x x a x =+-.（I ）讨论()f x 的单调性；（II ）当()f x 有最大值,且最大值大于22a -时,求a 的取值范围.32.(2017·全国Ⅰ文，21)已知函数f (x )＝e x (e x －a )－a 2x .(1)讨论f (x )的单调性；(2)若f (x )≥0，求a 的取值范围．1．解 (1)函数f (x )的定义域为(－∞，＋∞)，f ′(x )＝2e 2x －a e x －a 2＝(2e x ＋a )(e x －a )． ①若a ＝0，则f (x )＝e 2x 在(－∞，＋∞)上单调递增． ②若a >0，则由f ′(x )＝0，得x ＝ln a . 当x ∈(－∞，ln a )时，f ′(x )<0； 当x ∈(ln a ，＋∞)时，f ′(x )>0.故f (x )在(－∞，ln a )上单调递减，在(ln a ，＋∞)上单调递增． ③若a <0，则由f ′(x )＝0，得x ＝ln ⎝⎛⎭⎫－a2. 当x ∈⎝⎛⎭⎫－∞，ln ⎝⎛⎭⎫－a 2时，f ′(x )<0； 当x ∈⎝⎛⎭⎫ln ⎝⎛⎭⎫－a 2，＋∞时，f ′(x )>0. 故f (x )在⎝⎛⎭⎫－∞，ln ⎝⎛⎭⎫－a 2上单调递减，在⎝⎛⎭⎫ln ⎝⎛⎭⎫－a 2，＋∞上单调递增． (2)①若a ＝0，则f (x )＝e 2x ，所以f (x )≥0.②若a >0，则由(1)知，当x ＝ln a 时，f (x )取得最小值，最小值为f (ln a )＝－a 2ln a ， 从而当且仅当－a 2ln a ≥0，即0＜a ≤1时，f (x )≥0.③若a <0，则由(1)知，当x ＝ln ⎝⎛⎭⎫－a 2时，f (x )取得最小值，最小值为f ⎝⎛⎭⎫ln ⎝⎛⎭⎫－a 2＝a 2⎣⎡⎦⎤34－ln ⎝⎛⎭⎫－a 2，从而当且仅当a 2⎣⎡⎦⎤34－ln ⎝⎛⎭⎫－a 2≥0，即a ≥－234e 时f (x )≥0.。