06 功率谱密度和白噪声过程解析
白噪声模型的建立
一、白噪声模型建立白噪声模型是由白噪声经过积分后得到的,是一种描述路面形态的最常用的数学模型。
通常把路面相对于基准平面的高度q ,沿道路走向长度I 的变化q(t),称为路面纵断面曲线,它服从高斯分布。
作为车辆输入的路面不平度,主要采用路面功率谱密度描述其统计特性。
在1984年国际标准化组织在文件ISO/TC 108/SC2N67中提出的“路面不平度表示方法草案”和国内长春汽车研究所草定制GB 7031《车辆输入——路面平度表示》标准之中,两个文件均建议路面功率谱Gq(n)用下市作为拟合表达式[4]:()cx q q G q G -⎪⎪⎭⎫⎝⎛=000 (1.1)式中: Gx 0(q)——路面功率谱密度 (m 2/m -1); q ——空间平率 (m -1),它是波长的λ的倒数; q 0——参考空间平率, q 0=0.1(m -1); G 0——路面不平度系数(m 2/m -1);c ——频率指数,一个常数,近似等于2。
根据国家标准,车辆输入路面平度表示方法,按功率谱密度将路面分为八级[4],如表2.1所示。
表2.1路面平度8级分类标准Table2.1 pavement roughness 8 classification standard路面不平对汽车产生的输入是和车速相关的。
时间频率f(1/s),汽车行驶速v(m/s)对空间频率为q (m -1)的路面不平度,三者之间的关系:qv f = (1.2)空间频率谱函数转化为与速度有关的时间频谱函数,有关系式()()Vq G f G x x 00=(1.3)将式(2.2)和式(2.3)代入上(2.1)最后推到的式:()cc cx f V q G f G 1000-=(1.4) 垂直位移的功率谱密度与垂直速度的功率谱密度的关系,如式()()()f G f f G x x 0022π= (1.5)如果c=2,则地面垂直速度功率谱密度描述为()()()V q G f G f f G x x 20224200ππ== (1.6)由上式(1.6)看出,如果w 一定,则地面垂直功率谱密度就是一个常数,可以看做是白噪声的过程。
白噪声

物理学概念
01 定义
03 参数 05 应用
目录
02 起源 04 通信中的
白噪声(white noise)是指功率谱密度在整个频域内是常数的噪声。所有频率具有相同能量密度的随机噪声 称为白噪声。
定义
白噪声是指在较宽的频率范围内,各等带宽的频带所含的噪声功率谱密度相等的噪声。
一般在物理上把它翻译成白噪声(white noise)。
人生充满声音和噪声干扰,如轿车鸣喇叭、汪汪狗叫、吵邻打鼾、警报器、大喊大叫.白噪声并不增加烦躁, 而是包含所有同等频率的声音.研究表明,一个稳定、平和的声音流,如白噪声、可过滤和分散噪音,可以帮助减轻 噪音分心,这也正是为什么它用来帮助人们放松、睡眠。
上市销售的白噪声机器产品有睡眠辅助器、私密性增强器以及掩饰耳鸣。
白噪声可以用于放大器或者电子滤波器的频率响应测试,有时它与响应平坦的话筒或和自动均衡器一起使用。 这个设计的思路是系统会产生白噪声,话筒接收到扬声器产生的白噪声,然后在每个频率段进行自动均衡从而得 到一个平坦的响应。这种系统用在专业级的设备、高端的家庭立体声系统或者一些高端的汽车收音机上。
白噪声也作为一些随机数字生成器的基础使用,常用于计算机科学领域。
白噪声的应用领域之一是建筑声学,为了减弱内部空间中分散人注意力并且不希望出现的噪声(如人的交谈), 使用持续的低强度噪声作为背景声音。
在电子通信中也有白噪声的应用,它被直接或者作为滤波器的输入信号以产生其它类型的噪声信号,尤其是 在信号合成中,经常用来重现有很高噪声成分信号。
白噪声也用来产生冲击响应。为了在一个演出地点保证音乐会或者其它演出的均衡效果,从P A系统发出一 个瞬间的白噪声或者粉红噪声,并且在不同的地方监测噪声信号,这样工程师就能够建筑物的声学效应能够自动 地放大或者削减某些频率,从而就可以调整总体的均衡效果以得到一个平衡的和声。
功率谱密度

功率谱密度谱是一种概率统计方法,是对随机变量均方值的量度。
一般用于随机振动分析,连续瞬态响应只能通过概率分布函数进行描述,即出现某水平响应所对应的概率。
功率谱密度是结构在随机动态载荷激励下响应的统计结果,是一条功率谱密度值—频率值的关系曲线,其中功率谱密度可以是位移功率谱密度、速度功率谱密度、加速度功率谱密度、力功率谱密度等形式。
数学上,功率谱密度值—频率值的关系曲线下的面积就是方差,即响应标准偏差的平方值。
谱是个很不严格的东西,常常指信号的Fourier变换,是一个时间平均(time average)概念功率谱的概念是针对功率有限信号的(能量有限信号可用能量谱分析),所表现的是单位频带内信号功率随频率的变换情况。
保留频谱的幅度信息,但是丢掉了相位信息,所以频谱不同的信号其功率谱是可能相同的。
有两个重要区别:1。
功率谱是随机过程的统计平均概念,平稳随机过程的功率谱是一个确定函数;而频谱是随机过程样本的Fourier变换,对于一个随机过程而言,频谱也是一个“随机过程”。
(随机的频域序列)2。
功率概念和幅度概念的差别。
此外,只能对宽平稳的各态历经的二阶矩过程谈功率谱,其存在性取决于二阶局是否存在并且二阶矩的Fourier变换收敛;而频谱的存在性仅仅取决于该随机过程的该样本的Fourier变换是否收敛。
热心网友回答提问者对于答案的评价:谢谢解答。
频谱分析(也称频率分析),是对动态信号在频率域内进行分析,分析的结果是以频率为坐标的各种物理量的谱线和曲线,可得到各种幅值以频率为变量的频谱函数F(ω)。
频谱分析中可求得幅值谱、相位谱、功率谱和各种谱密度等等。
频谱分析过程较为复杂,它是以傅里叶级数和傅里叶积分为基础的。
功率谱是个什么概念?它有单位吗?随机信号是时域无限信号,不具备可积分条件,因此不能直接进行傅氏变换。
一般用具有统计特性的功率谱来作为谱分析的依据。
功率谱与自相关函数是一个傅氏变换对。
功率谱具有单位频率的平均功率量纲。
通信原理第六版课后思考题答案

通信原理第六版课后思考题答案第一章绪论1.1以无线广播和电视为例,说明图1-1模型中的信息源,受信者及信道包含的具体内容是什么在无线电广播中,信息源包括的具体内容为从声音转换而成的原始电信号,收信者中包括的具体内容就是从复原的原始电信号转换乘的声音;在电视系统中,信息源的具体内容为从影像转换而成的电信号。
收信者中包括的具体内容就是从复原的原始电信号转换成的影像;二者信道中包括的具体内容分别是载有声音和影像的无线电波1.2何谓数字信号,何谓模拟信号,两者的根本区别是什么数字信号指电信号的参量仅可能取有限个值;模拟信号指电信号的参量可以取连续值。
他们的区别在于电信号参量的取值是连续的还是离散可数的1.3何谓数字通信,数字通信有哪些优缺点传输数字信号的通信系统统称为数字通信系统;优缺点:数字通行系统的模型见图1-4所示。
其中信源编码与译码功能是提高信息传输的有效性和进行模数转换;信道编码和译码功能是增强数字信号的抗干扰能力;加密与解密的功能是保证传输信息的安全;数字调制和解调功能是把数字基带信号搬移到高频处以便在信道中传输;同步的功能是在首发双方时间上保持一致,保证数字通信系统的有序,准确和可靠的工作。
1-5按调制方式,通信系统分类?根据传输中的信道是否经过调制,可将通信系统分为基带传输系统和带通传输系统。
1-6按传输信号的特征,通信系统如何分类?按信号特征信道中传输的信号可分为模拟信号和数字信号,相应的系统分别为模拟通信系统和数字通信系统。
1-7按传输信号的复用方式,通信系统如何分类?频分复用,时分复用,码分复用。
1-8单工,半双工及全双工通信方式是按什么标准分类的?解释他们的工作方分为并行传输和串行传输。
并行传输是将代表信息的数字信号码元以组成的方式在两条或两条以上的并行信道上同时传输,其优势是传输速度快,无需附加设备就能实现收发双方字符同步,缺点是成本高,常用于短距离传输。
串行传输是将代表信息的数字码元以串行方式一第1/10页个码元接一个码元地在信道上传输,其优点是成本低,缺点是传输速度慢,需要外加措施解决收发双方码组或字符同步,常用于远距离传输。
白噪声
4.3 理想白噪声、带限白噪声比较分析1、实验原理若一个具有零均值的平稳随机过程,其功率谱密度在某一个有限频率范围内均匀分布,而在此范围外为零,则称这个过程为带限白噪声。
带限白噪声分为低通型和带通型。
白噪声详细描述可参考马文平、李兵兵等编著.随机信号分析与应用.科学出版社,2006出版的书第2章节。
朱华、黄辉宁、李永庆、梅文博.随机信号分析.北京理工大学出版社,2000出版的书第4章节。
以及与随机信号分析相关的参考书籍。
2、实验任务与要求⑴通过实验掌握白噪声的特性以及带限白噪声的意义,重点在于系统测试与分析。
算法选用matlab或c/c++语言之一编写和仿真程序。
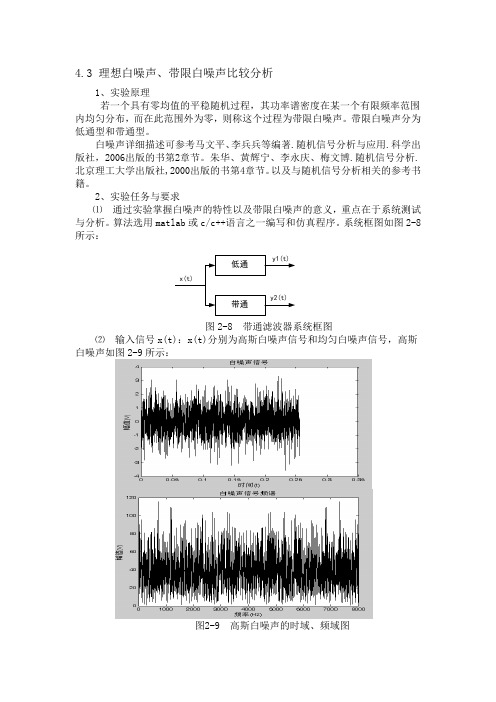
系统框图如图2-8所示:低通带通x(t)y1(t)y2(t)图2-8带通滤波器系统框图⑵输入信号x(t):x(t)分别为高斯白噪声信号和均匀白噪声信号,高斯白噪声如图2-9所示:图2-9 高斯白噪声的时域、频域图要求测试白噪声的均值、均方值、方差,自相关函数、概率密度、频谱及功率谱密度并绘图。
分析实验结果,搞清楚均值、均方值、方差,自相关函数、频谱及功率谱密度的物理意义。
例:均值除了表示信号的平均值,它还表示信号中有了什么成分。
相关函数当τ=0时为什么会有一个冲击,表示什么,它又等于什么。
信号的时域波形有哪些特征,频域又有哪些特征。
频谱及功率谱密度有什么差异,什么噪声是白噪声,这个噪声符合白噪声的定义吗等等。
⑶设计一个低通滤波器和一个带通滤波器。
要求白噪声分别通过低通滤波器和带通滤波器后的信号能够表现出带限白噪声的特点。
测试低通滤波器和一个带通滤波器的时频特性和频域特性以验证其正确性。
⑷分别计算高斯白噪声、均匀白噪声经低通滤波、带通滤波器后的均值、均方值、方差、概率密度、自相关函数、频谱及功率谱密度,并加以分析。
⑸所有结果均用图示法来表示。
⑹白噪声在什么情况下为带限白噪声?⑺按要求写实验报告。
第4章 随机信号的功率谱密度

确知信号的能量谱密度与功率谱密度 非周期信号的能量为: ∵ 非周期信号的能量为:
1 W = lim ∫ x ( t )dt = T → ∞ −T 2π
T 2 T
∫
∞
−∞
| X T ( ω ) | dω = ∫ | X T ( f ) | df
−∞
2
∞
2
其中, 为一付氏变换对; 其中 xT ( t ) ⇔ XT ( ω ) 为一付氏变换对
为功率型平稳随机信号。 设 X( t )为功率型平稳随机信号。 由于随机信号的每一样本函数( 或实现) 由于随机信号的每一样本函数 ( 或实现 ) 都是一个确 因此, 定的时间函数 x(t , ξ i ) ,因此,对于每个样本函数都可以求 得对应的功率谱密度函数, 得对应的功率谱密度函数,即 | xT (t , ξi ) |2 | XT (ω , ξi ) |2 GX (ω , ξ i ) = lim = lim , T →∞ T →∞ 2T 2T
称为白噪声过程 简称白噪声 白噪声过程, 白噪声。 的平稳过程 N( t ),称为白噪声过程,简称白噪声。 W 其中, 为正实常数,单位: 其中, N 0 为正实常数,单位: Hz
白噪声的功率谱函数和自相关函数为: 白噪声的功率谱函数和自相关函数为:
N0 G N ( ω ) = 2 , ω ∈ ( −∞ ,+∞ ) N0 R N (τ ) = δ (τ ) 2
1 G X ( ω ) = lim T → ∞ 2T
+∞
∫
T −t
−T − t
[∫
T −T
T
−T
R X ( t , t + τ )dt ] e − jωτ d τ
1 = ∫ [ lim − ∞ T → ∞ 2T
功率谱密度和白噪声过程 PPT
R() 1
S()cos()d
0
Xtcosct
0, 2
R(
)
1 2
cosc
S()
R()ejd 1
2
cosce jd
1
e e j(c )
j(c )
d
4
2
(
c
)
(
c
)
R() e||
S() R()ejd e||ejd
2 e || 0
cosd222
S()4 1 20 4 29,求 R()
2) |SX Y()|2SX()SY()
3) Re[SXY()]Re[SXY()] 奇函数 Im[SXY()]Im[SXY()] 偶函数
1 ) S X Y() S Y * X () S Y X ()
先证明: R Y *X()R YX()
R YX()y(t)x*(t)f(x,t;y,t)dxdy
2 X
lim
T
E
1 2T
T
X
2
(t
)dt
T
lim 1 T E[ X 2 (t)]dt T 2T T
P X2 1 T li m 2 1 TE [|F X(,T)|2]d
SX()T li m 2 1 TE|F X(,T)|2
为平稳随机过程X(t)的功率谱密度。
这样,Px又可以写成
W s2 (t)d t ? |s(t)|d t
E()| F()|2
由巴塞伐尔等式,可得到
s2(t)dt21 |F()|2d
信号的总能量
信号的能谱密度
能量守恒!
能量无限,平均功率有限的信号称 为功率型信号。即
Ps T li m 21T
第七讲 功率谱密度分解
从本例的求解过程可得 RX ( ) ai cos( i )
i 1
的谱密度:
S X ( ) a i [ ( i ) ( i )]
n i 1
例2 已知平稳过程 { X t } 具有如下功率谱密度: 2 4 S X 4 10 2 9 求平稳过程相关函数及平均功率 。
四
1
平稳随机过程的功率谱密度
平均功率与功率谱密度的定义
X ( t )dt 为平稳过程的平均功率 2T T
T 2
定义8 1 lim E 称T
T 1 2 2 由此易得:lim E X ( t ) dt R ( 0 ) X X T 2T T 从而有平稳过程的平均功率等于过程的均方值,
2 S X ( ) , 0 G X ( ) , 0 0
相应地 S X ( ) 可称为“双边功率谱”它 们的图形关系如图所示。
G X ( )
S X ( )
0
性质4
有理谱密度是实际应用中最常
见的一类功率谱密度。其形式必为:
a2 n 2 a S X S0 2 m 2m2 b2 m 2 b 式中 S0 0 。上式要求有理函数的分 子、分母只出现偶次项的原因是因 S X ( ) 为偶函数,又由于要求平均功率有限,所
白噪声 在电路系统分析、自动控制和测量中经 常遇到一类随机干扰—“白噪声” ,因为在电 路系统中,由于分子的热运动,使电路各处 的电流或电压受到随机干扰,在系统分析中 也把随机干扰称为噪声,因为这种电压或电 流的变化反映为声波的变化时,就是人们不 爱听的嘶嘶嚓嚓的声音,从数学上看,这就
五
《测试技术》(第二版)课后习题参考答案
《测试技术》(第二版)课后习题参考答案解:(1) 瞬变信号-指数衰减振荡信号,其频谱具有连续性和衰减性。
(2) 准周期信号,因为各简谐成分的频率比为无理数,其频谱仍具有离散性。
(3) 周期信号,因为各简谐成分的频率比为无理数,其频谱具有离散性、谐波性和收敛性。
解:x(t)=sin2t f 0π的有效值(均方根值):2/1)4sin 41(21)4sin 41(21)4cos 1(212sin 1)(100000000000002020000=-=-=-===⎰⎰⎰T f f T T tf f T T dt t f T dt t f T dt t x T x T T T T rms ππππππ 解:周期三角波的时域数学描述如下:(1)傅里叶级数的三角函数展开:,式中由于x(t)是偶函数,t n 0sin ω是奇函数,则t n t x 0sin )(ω也是奇函数,而奇函数在上下限对称区间上的积分等于0。
故=n b 0。
因此,其三角函数展开式如下:其频谱如下图所示:⎪⎪⎪⎩⎪⎪⎪⎨⎧+≤≤-≤≤-+=)(202022)(0000nT t x T t t T AA t T t T A A t x 21)21(2)(12/0002/2/00000=-==⎰⎰-T T T dt t T T dt t x T a ⎰⎰-==-2/00002/2/00000cos )21(4cos )(2T T T n dt t n t T T dt t n t x T a ωω⎪⎩⎪⎨⎧==== ,6,4,20,5,3,142sin 422222n n n n n πππ⎰-=2/2/0000sin )(2T T n dtt n t x T b ω∑∞=+=1022cos 1421)(n t n nt x ωπ∑∞=++=1022)2sin(1421n t n nπωπ(n =1, 3, 5, …)(2)复指数展开式复指数与三角函数展开式之间的关系如下:)( 21=212121n 22000=-===+====nn n e n m n n n n n a barctg C R C I arctg a A b a C a A C φ A ϕ单边幅频谱 单边相频谱0 ωn φω0 3ω0 5ω0 -ω0 -3ω0 -5ω00 ωI m C nω0 3ω0 5ω0 -ω0 -3ω0 -5ω0虚频谱双边相频谱解:该三角形窗函数是一非周期函数,其时域数学描述如下:用傅里叶变换求频谱。
白噪声
白噪声白噪声是指功率谱密度在整个频域内均匀分布的噪声。
所有频率具有相同能量密度的随机噪声称为白噪声。
从我们耳朵的频率响应听起来它是非常明亮的“咝”声(每高一个八度,频率就升高一倍。
因此高频率区的能量也显著增强)。
1概述白噪声是指在较宽的频率范围内,各等带宽的频带所含的噪声能量相等的噪声。
一般在物理上把它翻译成白噪声(white noise)。
白噪声或白杂讯,是一种功率频谱密度为常数的随机信号或随机过程。
换句话说,此信号在各个频段上的功率是一样的,由于白光是由各种频率(颜色)的单色光混合而成,因而此信号的这种具有平坦功率谱的性质被称作是“白色的”,此信号也因此被称作白噪声。
相对的,其他不具有这一性质的噪声信号被称为有色噪声。
理想的白噪声具有无限带宽,因而其能量是无限大,这在现实世界是不可能存在的。
实际上,我们常常将有限带宽的平整讯号视为白噪音,因为这让我们在数学分析上更加方便。
然而,白噪声在数学处理上比较方便,因此它是系统分析的有力工具。
一般,只要一个噪声过程所具有的频谱宽度远远大于它所作用系统的带宽,并且在该带宽中其频谱密度基本上可以作为常数来考虑,就可以把它作为白噪声来处理。
例如,热噪声和散弹噪声在很宽的频率范围内具有均匀的功率谱密度,通常可以认为它们是白噪声。
当你需要专心工作,而周遭总是有繁杂的声音时,就可以选用这两种声音来加以遮蔽。
一般来说,通常的情况下你可以选用白色噪音,而粉红色噪音则是特别针对说话声的遮蔽材料。
粉红色噪音又被称做频率反比(1/f) 噪音,因为它的能量分布与频率成反比,或者说是每一个八度音程(Octave) 能量就衰退3 dB。
高斯白噪声高斯白噪声:如果一个噪声,它的幅度分布服从高斯分布,而它的功率谱密度又是均匀分布的,则称它为高斯白噪声。
热噪声和散粒噪声是高斯白噪声。
所谓高斯白噪声中的高斯是指概率分布是正态函数,而白噪声是指它的二阶矩不相关,一阶矩为常数,是指先后信号在时间上的相关性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S ( ) R ( )e d R( )e S ( ) R ( )e d R( )e
* j
d S ( )
j ( )
d S ( )
功率谱密度的性质
由于R(τ)和S(ω)都是偶数,于是维
纳-辛钦公式还可以写成:
1、谱密度与自相关函数的关系
平稳随机过程的功率谱密度是它的自 相关函数的傅立叶变换:
S () R( )e
j
d
①
由于
R( ) R ( ) S ( ) 是实函数
*
谱密度与自相关函数的关系
由傅立叶逆变换公式,有
1 R ( ) 2
S ( )e j d
1 PX 2
1 2 lim E [| F ( , T ) | ] d X T 2T
平稳过程的功率谱密度
定义
1 2 S X ( ) lim E | FX ( , T ) | T 2T 为平稳随机过程X(t)的功率谱密度。 这样,Px又可以写成
1 PX 2
1 s (t )dt 2
2
| F ( ) | d
2
信号的总能量
信号的能谱密度
能量守恒!
4、功率型信号
能量无限,平均功率有限的信号称
为功率型信号。即
1 Ps lim T 2T
T
T
s (t )dt
2
Ps为信号的平均功率。
5、平均功率的谱表示
功率型信号不满足绝对可积条件。 为了能够利用傅立叶变换给出平均
P sT
Байду номын сангаас
s (t )dt
2 T
平均功率的谱表示
由巴塞伐尔等式,可得到
1 2 s (t )dt 2 | F (, T ) | d 两边同除以2T,并由截尾函数的定 义,得到
2 T
1 2T
1 T s (t )dt 4 T
T 2
随机电报信号自相关函数
R( ) e
| |
求功率谱密度
S ( ) R( )e
j
d e
| | j
e
d
2 e
0
| |
2 cos d 2 2
例 2.4-3
2 4 已知功率谱 S ( ) 4 , 求R( ) 2 10 9
* YX * YX j
d
RYX ( )e
j ( )
d SYX ( )
互谱密度函数不是实的、正的偶函数
2) | S XY () | S X ()SY ()
从定义
1 S XY ( ) lim E{FX ( , T ) FY ( , T )} T 2T
功率谱密度两种定义的等价条件
通过变量置换,最后得到:
| | j S X ( ) lim (1 ) R( )e d T 2T 2T 2T 2T | | j j lim R( )e d lim R( )e d T 2T T 2T 2T
2、互谱密度的维纳-辛钦公式
随机过程X(t)和Y(t)的互谱密度是
它们的互相关函数RXY(τ)的傅立叶 变换:
S XY ( ) RXY ( )e
j
d
d
1 RXY ( ) 2
S XY ( )e
j
2、互谱密度的维纳-辛钦公式
当
0
1 RXY (0) 2
②
上述两式统称为 维纳-辛钦公式 注释:对比“信号与系统” 中维纳辛钦公式
返回
2、功率谱密度两种定义的等价条件
对于第一种定义,将其展开
T 1 T jt1 S X ( ) lim E X (t1 )e dt1 X (t2 )e jt2 dt2 T T 2T T 1 T T j ( t1 t2 ) lim E [ X ( t ) X ( t )] e dt1dt2 1 2 T 2T T T 1 T T j ( t1 t2 ) lim R ( t t ) e dt1dt2 1 2 T 2T T T
1 z 2 +4 j|τ|z R(τ)= 2πj 2 e 在z=j,3j留数和 2 2π (z +1)(z +9) 1 (9e | | 5e 3| | ) 48
1 R( ) 2 应用留数定理
4 j e 4 10 2 9 d
| s(t ) | dt 的情况下,能量型
dt
称F(ω)为信号s(t)的频谱。
W s (t )dt | s(t ) | dt
2
?
3、信号的能谱密度
能量型信号的能谱E(ω)为
E() | F () |2
由巴塞伐尔等式,可得到
S X ( )d
平均功率谱 的表达式
平稳过程的功率谱密度
S X ( ) 为双边功率谱密度,但在实际
应用中,负频率不存在,故引入
单边谱密度
2S X ( ) 0 GX ( ) 0 0
二、谱密度与自相关函数
1、功率谱密度与自相关函数的关
系—维纳-辛钦公式 2、功率谱密度两种定义的等价条件 3、功率谱密度的性质
2 2
S ( )
1
, 求R( )
三、互谱密度
1、互谱密度的定义 2、互谱密度的维纳-辛钦公式形式定义
3、互谱密度的性质
1、互谱密度的定义
定义:
设随机过程X(t)和Y(t)是联合平稳 的,则定义互谱密度为
1 S XY ( ) lim E{FX ( , T ) FY ( , T )} T 2T
| F ( , T ) | d
2
平均功率的谱表示
令T趋于无穷,功率型信号s(t)在
(-∞, ∞)上的平均功率可表示为
1 T 2 Ps lim s ( t ) dt T 2T T 1 1 2 lim | F ( , T ) | d 2 T 2T
第六讲:
平稳随机过程的功率谱密度 白噪声随机过程
主讲人:张有光 电 话:82314978 办公室:新主楼F806
主要内容
一、平稳过程的功率谱密度 二、谱密度与自相关函数
三、平稳过程的互谱密度
四、白噪声过程
一、平稳过程的功率谱密度
1、能量型信号 2、信号的频谱
3、信号的能谱
功率型信号的平均功率谱密度
功率谱密度
功率型信号的平均功率谱密度,简
称功率谱密度,定义为:
1 2 S lim | F ( , T ) | T 2T
6、平稳过程的功率谱密度
平稳随机过程的样本函数是功率型的。 T FX ( , T ) X (t )e jt dt T
S XY ( )d E[ X (t )Y (t )]
若X(t)是一个二端电压、Y(t)是流经
该器件的电流,则上式左边就是消 耗的功率。
两个正交随机过程性质
随机过程X(t)和Y(t)正交
RXY ( ) 0, S XY () 0
此时有:
RX Y ( ) RX ( ) RY ( ) S X Y ( ) S X ( ) SY ( )
3、互谱密度的性质
1) SXY () S () SYX ()
* YX
2) | S XY () | S X ()SY ()
2
3)
Re[S XY ( )] Re[S XY ()]
奇函数
Im[S XY ()] Im[S XY ()] 偶函数
1 )SXY () S () SYX ()
2T
功率谱密度两种定义的等价条件
只要
| R( ) | d
j
则上式中第二项为零,故此时
S X ( ) R( )e
d
也就是说,平稳随机过程在自相关
函数绝对可积的情况下,维纳-辛
钦公式成立。此时功率谱密度的两 种定义等价。
功率谱的意义
1 j R ( ) S ( ) e d 2 令 0, 则 1 R (0) 2
S ( ) d E{| X (t ) | } 0
2
3、功率谱密度的性质
若过程X(t)是实平稳的,则自相关函
数是实偶函数,因此功率谱密度也 是实偶函数,即
证明:
S () S (), S () S ()
* j j ( )
* YX
先证明: R ( ) RYX ( )
* YX
RYX ( ) y (t ) x (t ) f ( x, t ; y, t )dxdy
*
令: t t * RYX ( ) x(t ) y (t ) f ( x, t ; y, t )dxdy RXY ( )
4、功率型信号
5、平均功率的谱表示和功率谱密度
6、平稳过程的功率谱密度
1、能量型信号
能量型信号
W s (t )dt
2
其中,s(t)为信号,W为总能量。
2、信号的频谱
