高二数学必修二第一章检测试题(含答案)
高中数学必修二第一章测试题及答案

�上面球一同在都点顶个 8 的它且�5�4�3 是别分长棱条三上点顶个一的体方长�4
3 4�D 3 3�C 3 2�B 3 �A
�)
2 �1 �D
2 �2 2
(为积面表的锥棱三的 1 是都长棱�3
2 �1 2
�C �)
�B
2 �2�A
(是积面的形图面平原么那�形梯腰等
的 1 为均底上和腰�°54 为角底个一是图观直测二斜的形图面平的置放平水个一果如�2 体面八正�D 柱棱�C 图视俯
则�a 为长棱的体方正若�心中的 DCBA 面底上是 O�中 1D1C1B1A�DCBA 体方正�31
�_____________是比之积体的们它则�3∶2∶1 是比之积面表的球个三若�21
�棱侧条________有台棱个一
的少最点顶�点顶个________有锥棱个一的少最数面�面个______有少至柱棱个一�11 题空填、二
� 3 3∶ 2 2∶1�3) 3 (∶3) 2 (∶31� 33r ∶ 32r ∶ 31r � 3 ∶ 2 ∶1�3r∶2r∶1r � 3 3∶ 2 2∶1�案答考参�21 �台棱三�锥棱三�柱棱三�是别分体何几的件条合符�析解 �3�4�5�案答考参�11 .D 选以所�体合组为且�圆为面底看图视三从�析解 D�01 题空填、二
652
21
2
(×π× �hS �2V
1 1
3
3
�4×2)
积体的库仓则�m 61 成变径直面底的库仓�一案方按果如�案答考参 )1(�解
3
61
2
(×π× �hS �1V
1 1
3
3
�02 �
�π
1h rπ 2
3
841 3 1
高中数学必修二测试题及答案人教版

第一章 空间几何体一、选择题1.有一个几何体的三视图如下图所示,这个几何体可能是一个( ).主视图 左视图 俯视图 (第1题) A .棱台 B .棱锥 C .棱柱 D .正八面体2.如果一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( ).A .2+2B .221+C .22+2 D .2+13.棱长都是1的三棱锥的表面积为( ).A .3B .23C .33D .434.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( ).A .25πB .50πC .125πD .都不对 5.正方体的棱长和外接球的半径之比为( ). A .3∶1 B .3∶2 C .2∶3 D .3∶36.在△ABC 中,AB =2,BC =1.5,∠ABC =120°,若使△ABC 绕直线BC 旋转一周,则所形成的几何体的体积是( ).A .29πB .27πC .25πD .23π7.若底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长分别是9和15,则这个棱柱的侧面积是( ).A .130B .140C .150D .1608.如图,在多面体ABCDEF 中,已知平面ABCD 是边长为3的正方形,EF ∥AB ,EF =23,且EF 与平面ABCD 的距离为2,则该多面体的体积为( ).A .29 B .5 C .6 D .2159.下列关于用斜二测画法画直观图的说法中,错误..的是( ). A .用斜二测画法画出的直观图是在平行投影下画出的空间图形B .几何体的直观图的长、宽、高与其几何体的长、宽、高的比例相同C .水平放置的矩形的直观图是平行四边形D .水平放置的圆的直观图是椭圆10.如图是一个物体的三视图,则此物体的直观图是( ).(第8题)(第10题)二、填空题11.一个棱柱至少有______个面,面数最少的一个棱锥有________个顶点,顶点最少的一个棱台有________条侧棱.12.若三个球的表面积之比是1∶2∶3,则它们的体积之比是_____________.13.正方体ABCD-A1B1C1D1 中,O是上底面ABCD的中心,若正方体的棱长为a,则三棱锥O-AB1D1的体积为_____________.14.如图,E,F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是___________.(第14题)15.已知一个长方体共一顶点的三个面的面积分别是2、3、6,则这个长方体的对角线长是___________,它的体积为___________.16.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米则此球的半径为_________厘米.三、解答题17.有一个正四棱台形状的油槽,可以装油190 L,假如它的两底面边长分别等于60 cm 和40 cm,求它的深度.18 *.已知半球内有一个内接正方体,求这个半球的体积与正方体的体积之比.[提示:过正方体的对角面作截面]19.如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=22,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.(第19题)20.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m,高4 m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4 m(高不变);二是高度增加4 m(底面直径不变).(1)分别计算按这两种方案所建的仓库的体积;(2)分别计算按这两种方案所建的仓库的表面积;(3)哪个方案更经济些?第一章 空间几何体参考答案A 组一、选择题 1.A解析:从俯视图来看,上、下底面都是正方形,但是大小不一样,可以判断可能是棱台.2.A解析:原图形为一直角梯形,其面积S =21(1+2+1)×2=2+2.3.A解析:因为四个面是全等的正三角形,则S 表面=4×43=3. 4.B解析:长方体的对角线是球的直径, l =2225+4+3=52,2R =52,R =225,S =4πR 2=50π. 5.C解析:正方体的对角线是外接球的直径. 6.D解析:V =V 大-V 小=31πr 2(1+1.5-1)=23π.7.D解析:设底面边长是a ,底面的两条对角线分别为l 1,l 2,而21l =152-52,22l =92-52,而21l +22l =4a 2,即152-52+92-52=4a 2,a =8,S 侧面=4×8×5=160. 8.D解析:过点E ,F 作底面的垂面,得两个体积相等的四棱锥和一个三棱柱,V =2×31×43×3×2+21×3×2×23=215.9.B解析:斜二测画法的规则中,已知图形中平行于 x 轴的线段,在直观图中保持原长度不变;平行于 y 轴的线段,长度为原来的一半.平行于 z 轴的线段的平行性和长度都不变.10.D解析:从三视图看底面为圆,且为组合体,所以选D. 二、填空题11.参考答案:5,4,3.解析:符合条件的几何体分别是:三棱柱,三棱锥,三棱台.12.参考答案:1∶22∶33.r 1∶r 2∶r 3=1∶2∶3,31r ∶32r ∶33r =13∶(2)3∶(3)3=1∶22∶33.13.参考答案:361a .解析:画出正方体,平面AB 1D 1与对角线A 1C 的交点是对角线的三等分点, 三棱锥O -AB 1D 1的高h =33a ,V =31Sh =31×43×2a 2×33a =61a 3. 另法:三棱锥O -AB 1D 1也可以看成三棱锥A -OB 1D 1,它的高为AO ,等腰三角形OB 1D 1为底面.14.参考答案:平行四边形或线段.15.参考答案:6,6.解析:设ab =2,bc =3,ac =6,则V = abc =6,c =3,a =2,b =1, l =1+2+3=6. 16.参考答案:12.解析:V =Sh =πr 2h =34πR 3,R =32764×=12. 三、解答题 17.参考答案:V =31(S +S S ′+S )h ,h =S S S S V ′+′+3=6001+4002+60030001903×=75.18.参考答案:如图是过正方体对角面作的截面.设半球的半径为R ,正方体的棱长为a ,则CC'=a ,OC =22a ,OC'=R .(第18题)在Rt △C'CO 中,由勾股定理,得CC' 2+OC 2=OC' 2,即 a 2+(22a )2=R 2. ∴R =26a ,∴V 半球=26πa 3,V 正方体=a 3. ∴V 半球 ∶V 正方体=6π∶2. 19.参考答案:S 表面=S 下底面+S 台侧面+S 锥侧面=π×52+π×(2+5)×5+π×2×22 =(60+42)π. V =V 台-V 锥 =31π(21r +r 1r 2+22r )h -31πr 2h 1 =3148π.20.解:(1) 参考答案:如果按方案一,仓库的底面直径变成16 m ,则仓库的体积V 1=31Sh =31×π×(216)2×4=3256π(m 3).如果按方案二,仓库的高变成8 m ,则仓库的体积COAV 2=31Sh =31×π×(212)2×8=3288π(m 3).(2) 参考答案:如果按方案一,仓库的底面直径变成16 m ,半径为8 m . 棱锥的母线长为l =224+8=45, 仓库的表面积S 1=π×8×45=325π(m 2). 如果按方案二,仓库的高变成8 m .棱锥的母线长为l =226+8=10,仓库的表面积S 2=π×6×10=60π(m 2).(3) 参考答案:∵V 2>V 1,S 2<S 1,∴方案二比方案一更加经济些.。
高二数学必修二第一章检测试题(含答案)
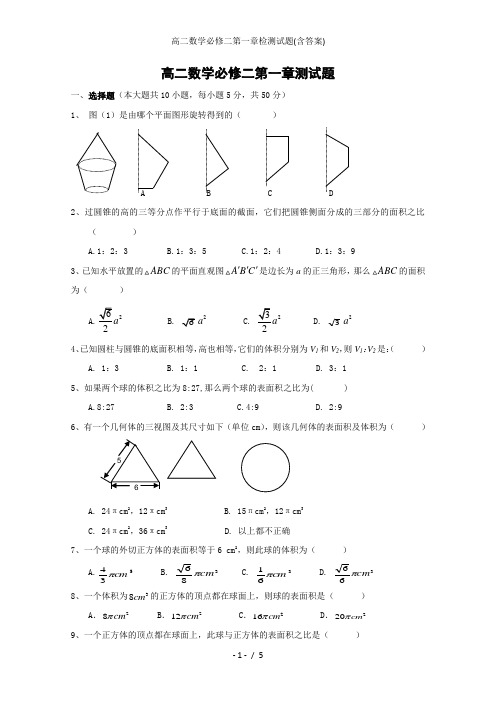
高二数学必修二第一章测试题一、选择题(本大题共10小题,每小题5分,共50分) 1、 图(1)是由哪个平面图形旋转得到的( )A B C D2、过圆锥的高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分的面积之比( )A.1:2:3B.1:3:5C.1:2:4D.1:3:93、已知水平放置的ABC 的平面直观图A B C '''是边长为a 的正三角形,那么ABC 的面积为( ) A.222a 2D. 32a4、已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为V 1和V 2,则V 1:V 2是:( )A. 1:3B. 1:1C. 2:1D. 3:1 5、如果两个球的体积之比为8:27,那么两个球的表面积之比为( )A.8:27B. 2:3C.4:9D. 2:96、有一个几何体的三视图及其尺寸如下(单位cm ),则该几何体的表面积及体积为( )A. 24πcm 2,12πcm 3B. 15πcm 2,12πcm 3C. 24πcm 2,36πcm3D. 以上都不正确7、一个球的外切正方体的表面积等于6 cm 2,则此球的体积为( )A.334cm π B.386cm π C. 361cm π D. 366cm π8、一个体积为38cm 的正方体的顶点都在球面上,则球的表面积是( )A .28cm πB .212cm πC .216cm πD .220cm π 9、一个正方体的顶点都在球面上,此球与正方体的表面积之比是( )A. 3πB. 4πC. 2π D. π10、如右图为一个几何体的三视图,其中府视图为正三角形,A 1B 1=2,AA 1=4,则该几何体的表面积为( )A. 6+3B. 24+3C. 24+23D. 32一、选择题答题表二、填空题(本大题共4小题,每小题5分,共20分)11. 长方体的共顶点的三个侧面面积分别为3,5,15,则它的体积为_______________. 12.一个半球的全面积为Q ,一个圆柱与此半球等底等体积,则这个圆柱的全面积是 . 13、从长方体的一个顶点出发的三条棱上各取一点E 、F 、G ,过此三点作长方体的截面,那么截去的几何体是_________.14、一个圆柱和一个圆锥的母线相等,底面半径也相等,则侧面积之比是_________.三、解答题(本大题共6小题,15、16、17、18每题13分,19、20每题14分,共80分) 15.将圆心角为1200,面积为3π的扇形,作为圆锥的侧面,求圆锥的表面积和体积.16. (如图)在底半径为2母线长为4的圆锥中内接一个高为3的圆柱,求圆柱 的表面积A B 1正视图侧视图府视图17、如图,在四边形ABCD中,,,,,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.18.已知长方体的全面积为11,十二条棱长度之和为24,求长方体的对角线的长。
高中数学必修二第一章测试题及答案(人教版)

第一章空间几何体一、选择题1.有一个几何体的三视图如下图所示,这个几何体可能是一个().主视图左视图俯视图(第1题)A.棱台B.棱锥C.棱柱D.正八面体2.如果一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是().A.2+2B.221+C.22+2D.2+13.棱长都是1的三棱锥的表面积为().A.3B.23C.33D.434.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是().A.25πB.50πC.125πD.都不对5.正方体的棱长和外接球的半径之比为().A.3∶1B.3∶2C.2∶3D.3∶36.在△ABC中,AB=2,BC=1.5,∠ABC=120°,若使△ABC绕直线BC旋转一周,则所形成的几何体的体积是().A.29πB.27πC.25πD.23π7.若底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长分别是9和15,则这个棱柱的侧面积是().A.130B.140C.150D.1608.如图,在多面体ABCDEF中,已知平面ABCD是边长为3的正方形,EF∥AB,EF=23,且EF与平面ABCD的距离为2,则该多面体的体积为().A.29B.5C.6D.2159.下列关于用斜二测画法画直观图的说法中,错误..的是().A.用斜二测画法画出的直观图是在平行投影下画出的空间图形B.几何体的直观图的长、宽、高与其几何体的长、宽、高的比例相同C.水平放置的矩形的直观图是平行四边形D.水平放置的圆的直观图是椭圆10.如图是一个物体的三视图,则此物体的直观图是().(第8题)(第10题)二、填空题11.一个棱柱至少有______个面,面数最少的一个棱锥有________个顶点,顶点最少的一个棱台有________条侧棱.12.若三个球的表面积之比是1∶2∶3,则它们的体积之比是_____________.13.正方体ABCD-A1B1C1D1中,O是上底面ABCD的中心,若正方体的棱长为a,则三棱锥O-AB1D1的体积为_____________.14.如图,E,F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是___________.(第14题)15.已知一个长方体共一顶点的三个面的面积分别是2、3、6,则这个长方体的对角线长是___________,它的体积为___________.16.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米则此球的半径为_________厘米.三、解答题17.有一个正四棱台形状的油槽,可以装油190 L,假如它的两底面边长分别等于60 cm和40cm,求它的深度.18 *.已知半球内有一个内接正方体,求这个半球的体积与正方体的体积之比.[提示:过正方体的对角面作截面]19.如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=22,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.(第20.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m ,高4 m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4 m(高不变);二是高度增加4 m (底面直径不变).(1)分别计算按这两种方案所建的仓库的体积;(2)分别计算按这两种方案所建的仓库的表面积;(3)哪个方案更经济些?第一章 空间几何体参考答案A 组一、选择题1.A解析:从俯视图来看,上、下底面都是正方形,但是大小不一样,可以判断可能是棱台.2.A解析:原图形为一直角梯形,其面积S =21(1+2+1)×2=2+2. 3.A解析:因为四个面是全等的正三角形,则S 表面=4×43=3. 4.B解析:长方体的对角线是球的直径,l =2225+4+3=52,2R =52,R=225,S =4πR2=50π. 5.C解析:正方体的对角线是外接球的直径.6.D解析:V =V 大-V 小=31πr 2(1+1.5-1)=23π. 7.D解析:设底面边长是a ,底面的两条对角线分别为l 1,l 2,而21l =152-52,22l =92-52,而21l +22l =4a 2,即152-52+92-52=4a2,a =8,S 侧面=4×8×5=160.8.D解析:过点E ,F 作底面的垂面,得两个体积相等的四棱锥和一个三棱柱,V =2×31×43×3×2+21×3×2×23=215.9.B解析:斜二测画法的规则中,已知图形中平行于x轴的线段,在直观图中保持原长度不变;平行于y 轴的线段,长度为原来的一半.平行于z 轴的线段的平行性和长度都不变.10.D解析:从三视图看底面为圆,且为组合体,所以选D.二、填空题11.参考答案:5,4,3.解析:符合条件的几何体分别是:三棱柱,三棱锥,三棱台.12.参考答案:1∶22∶33.r 1∶r2∶r 3=1∶2∶3,31r ∶32r ∶33r =13∶(2)3∶(3)3=1∶22∶33.13.参考答案:361a . 解析:画出正方体,平面A B1D 1与对角线A 1C 的交点是对角线的三等分点,三棱锥O -AB 1D 1的高h =33a ,V =31Sh =31×43×2a 2×33a =61a3. 另法:三棱锥O-A B1D1也可以看成三棱锥A -OB 1D 1,它的高为AO ,等腰三角形OB 1D1为底面.14.参考答案:平行四边形或线段. 15.参考答案:6,6.解析:设a b=2,b c=3,ac =6,则V = abc =6,c =3,a =2,b =1,l =1+2+3=6. 16.参考答案:12.解析:V =Sh =πr2h=34πR 3,R =32764×=12. 三、解答题17.参考答案:V =31(S +S S ′+S)h ,h=S S S S V ′+′+3=6001+4002+60030001903×=75.18.参考答案:如图是过正方体对角面作的截面.设半球的半径为R ,正方体的棱长为a ,则CC'=a ,OC =22a ,OC'=R .(第18题) 在Rt △C'CO 中,由勾股定理,得CC'2+OC 2=OC'2,即 a 2+(22a )2=R2. ∴R =26a ,∴V 半球=26πa3,V 正方体=a 3.C OA∴V 半球 ∶V 正方体=6π∶2.19.参考答案:S表面=S 下底面+S 台侧面+S锥侧面=π×52+π×(2+5)×5+π×2×22=(60+42)π.V =V 台-V 锥 =31π(21r +r 1r 2+22r )h -31πr 2h 1 =3148π. 20.解:(1) 参考答案:如果按方案一,仓库的底面直径变成16 m,则仓库的体积V1=31Sh =31×π×(216)2×4=3256π(m 3). 如果按方案二,仓库的高变成8 m ,则仓库的体积V2=31Sh =31×π×(212)2×8=3288π(m 3). (2) 参考答案:如果按方案一,仓库的底面直径变成16 m,半径为8 m . 棱锥的母线长为l =224+8=45,仓库的表面积S1=π×8×45=325π(m 2).如果按方案二,仓库的高变成8 m.棱锥的母线长为l =226+8=10,仓库的表面积S 2=π×6×10=60π(m 2).(3) 参考答案:∵V 2>V 1,S2<S 1,∴方案二比方案一更加经济些.。
(完整版)高中数学必修二第一章同步练习(含答案).docx

(完整版)高中数学必修二第一章同步练习(含答案).docx.1.1.1 柱、锥、台、球的的结构特征练习一一、选择题1、下列命题中,正确命题的个数是()(1 )桌面是平面;( 2)一个平面长 2 米,宽 3 米;( 3)用平行四边形表示平面,只能画出平面的一部分;(4)空间图形是由空间的点、线、面所构成。
A 、 1B、2C、3D、42、下列说法正确的是()A、水平放置的平面是大小确定的平行四边形B、平面ABCD就是四边形ABCD 的四条边围来的部分C、100 个平面重叠在一起比10 个平面重叠在一起厚D、平面是光滑的,向四周无限延展的面3、下列说法中表示平面的是()A、水面B、屏面C、版面D、铅垂面4、下列说法中正确的是()A、棱柱的面中,至少有两个面互相平行B、棱柱的两个互相平行的平面一定是棱柱的底面C、棱柱的一条侧棱的长叫做棱柱的高D、棱柱的侧面是平行四边形,但它的底面一定不是平行四边形5、长方体的三条棱长分别是AA /=1 , AB=2 ,AD=4 ,则从 A 点出发,沿长方体的表面到C/的最短距离是()A、5C、29D、376、若正棱锥的底面边长与侧棱长相等,则该棱锥一定不是()A、三棱锥B、四棱锥C、五棱锥D、六棱锥]7、过球面上两点可能作出球的大圆()A、0 个或 1 个B、有且仅有 1 个C、无数个D、一个或无数个8、一个圆柱的母线长为 5 ,底面半径为2,则圆柱的轴截面的面积为()A、10B、20二、填空题9、用一个平面去截一个正方体,截面边数最多是----------------条。
10、正三棱台的上、下底面边长及高分别为1、 2、 2,则它的斜高是------------。
11、一个圆柱的轴截面面积为Q,则它的侧面面积是----------------。
12、若圆锥的侧面面积是其底面面积的2 倍,则这个圆锥的母线与底面所成的角为----------------,圆锥的侧面展开图扇形的圆心角为----------------。
人教B高中数学必修二课时跟踪检测:第一章 立体几何初步 含解析

第一章立体几何初步1.1空间几何体1.1.7柱、锥、台和球的体积课时跟踪检测[A组基础过关]1.某三棱锥的三视图如图所示,该三棱锥的体积为()A.2 B.3C.4 D.6解析:由三视图可知三棱锥的直观图如图所示.其中AB为高,底面是直角三角形,V=13AB×12BD×CD=13×2×12×3×2=2,故选A.答案:A2.某几何体的三视图如图所示,则该几何体的体积为()A.13+π B.23+πC.13+2π D.23+2π解析:由该几何体的三视图可知该几何体是由一个三棱锥和半个圆柱组合而成,由此可知该几何体的体积为13×12×2×1×1+12π×12×2=13+π,故选A.答案:A3.某几何体的三视图如图所示,其中俯视图是等腰三角形,那么该几何体的体积是()A.96 B.128C.140 D.152解析:由三视图可知,该几何体是一个三棱柱,V=S·h=12×6×4×8=96.答案:A4.正三棱柱的侧面展开图是边长为2和4的矩形,则该正三棱柱的体积是()A.839B.439C.239D.439或839解析:当2为正三棱柱的底面周长时,正三棱柱底面三角形的边长a=2 3,底面面积S=34a2=39,正三棱柱的高h=4,所以正三棱柱的体积V=Sh=439;同理,当4为正三棱柱的底面周长时,正三棱柱底面三角形的边长a′=43,底面面积S′=34a′2=439,正三棱柱的高h′=2,所以正三棱柱的体积V′=S′h′=839.所以正三棱柱的体积为439或839.答案:D5.若正方体的棱长为2,则以该正方体各个面的中心为顶点的凸多面体的体积为()A.26B.23C.33D.23解析:以正方体各个面的中心为顶点的凸多面体是由两个全等的正四棱锥构成,正四棱锥的底面边长为1,高为22,∴V=2×13×1×1×22=23.故选B.答案:B6.已知圆锥的母线长为5,侧面积为20π,则此圆锥的体积为________.解析:由S侧=πrl=20π,l=5得r=4,∴圆锥的高h=l2-r2=3.∴圆锥的体积为V=13πr2·h=16π.答案:16π7.(2018·江苏卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.解析:由图可知,该多面体为两个全等正四棱锥的组合体,且正四棱锥的高为1,底面正方形的边长等于2,所以该多面体的体积为2×13×1×(2)2=43.答案:438.已知某几何体的俯视图是边长分别为8和6的矩形,主视图是一个底边长为8,高为4的等腰三角形,左视图是一个底边长为6,高为4的等腰三角形.(1)求该几何体的体积; (2)求该几何体的侧面积.解:由已知可得该几何体是一个底面为矩形,高为4,顶点在底面的射影是矩形中心的四棱锥V -ABCD .如图所示,(1)V =13×(8×6)×4=64.(2)该四棱锥有两个侧面VAD ,VBC 是全等的等腰三角形,且BC 边上的高为h 1=42+⎝ ⎛⎭⎪⎫822=42,另两个侧面VAB ,VCD 也是全等的等腰三角形,AB边上的高为h 2=42+⎝ ⎛⎭⎪⎫622=5,因此S 侧=2×⎝ ⎛⎭⎪⎫12×6×42+12×8×5=40+24 2.[B 组 技能提升]1.一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为( )A.18B.17C.16D.15解析:由三视图可知,正方体被平面截去三棱锥A1-AB1D1,设正方体的边长为a,V正=a3,VA1-AB1D1=13×12a2·a=16a3,∴V A1-AB1D1V剩=16a3a3-16a3=15,故选D.答案:D2.一个正方体的顶点都在球面上,它的棱长为3,则这个球的体积为() A.9π B.932πC.27π D.2732π解析:∵棱长为3的正方体的体对角线长为33,∴球半径为332,∴V=43π⎝⎛⎭⎪⎫3233=2732π.故选D.答案:D3.一个底面半径为R的圆柱形水桶中装有适量的水,若放入一个半径为r的实心铁球(水面漫过球),水面高度恰好升高r,则Rr=________.解析:由题知43πr3=πR2·r,∴R r=233.答案:23 34.已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的主视图如图所示,则该三棱锥的体积是________.解析:由主视图知,三棱锥的高为1,底面是腰长为2,底边为23的等腰三角形,∴V=13×12×23×1×1=33.答案:3 35.如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的主视图和左视图在下面画出(单位:cm).(1)在主视图下面,按照画三视图的要求画出该多面体的俯视图;(2)按照给出的尺寸,求该多面体的体积.解:(1)如图.(2)所求多面体的体积V=V长方体-V正三棱锥=4×4×6-13×⎝⎛⎭⎪⎫12×2×2×2=2843.6.圆台的母线长为6 cm,它的轴截面等腰梯形的一条对角线与一腰垂直且与下底所成的角为30°,求该圆台的体积.解:如图,等腰梯形AA1B1B为圆台的轴截面,AA1=6 cm,∠AA1B=90°,∠ABA1=30°,于是AB=2AA1=12 cm,由A1B1∥AB,得∠B1A1B=∠A1BA=30°,又∠A=90°-30°=60°,得∠A1BB1=60°-30°=30°,故△A1B1B为等腰三角形,∴A1B1=B1B=6 cm.又OO1·AB=AA1·A1B得,OO1=AA1·A1BAB=6×6312=33(cm),由圆台的体积公式:V圆台=13π·OO1·(A1O21+A1O1·AO+AO2)=13·π·33·(32+3×6+62)=633π(cm3).。
人教版高中数学必修二第一章单元测试(一)及参考答案
2018-2019学年必修二第一章训练卷空间几何体(一)注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)1.已知某空间几何体的三视图如图所示,则此几何体为( )A.圆台B.四棱锥C.四棱柱D.四棱台2.如图,△O ′A ′B ′是水平放置的△OAB 的直观图,则△OAB 的面积为( )A.6B.32C.62D.123.已知一个底面是菱形的直棱柱的侧棱长为5,菱形的对角线的长分别是9和15,则这个棱柱的侧面积是( ) A.3034B.6034C.3034135+D.1354.半径为R 的半圆卷成一个圆锥,则它的体积为( ) A.3324R π B.338R π C.3525R π D.358R π 5.已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为V 1和V 2,则V 1:V 2=( ) A.1:3B.1:1C.2:1D.3:16.若一个底面是正三角形的三棱柱的正视图如下图所示,其顶点都在一个球面上,则该球的表面积为( )A.163π B.193π C.1912π D.43π 7.一个正方体的体积是8,则这个正方体的内切球的表面积是( ) A.8πB.6πC.4πD.π8.如图是一个空间几何体的三视图,如果直角三角形的直角边长均为1,那么这个几何体的体积为( )A.1B.12 C.13D.169.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧度为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有( )此卷只装订不密封班级 姓名 准考证号 考场号 座位号A.14斛B.22斛C.36斛D.66斛10.正三棱柱有一个半径为3cm 的内切球,则此棱柱的体积是( ) A.393cmB.354cmC.327cmD.3183cm11.如图,网格纸上正方形小格的边长为1(表示1cm ),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm ,高为6cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.1312.如图,有一个水平放置的透明无盖的正方体容器,容器高8cm ,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm ,如果不计容器的厚度,则球的体积为( )A.3500cm 3πB.3cm 3866πC.3cm 31372π D.3cm 32048π二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的________(填入所有可能的几何体前的编号).①三棱锥;②四棱锥;③三棱柱;④四棱柱;⑤圆锥;⑥圆柱.14.用斜二测画法画边长为2的正三角形的直观图时,如果在已知图形中取的x 轴和正三角形的一边平行,则这个正三角形的直观图的面积是__________________. 15.棱锥的高为16,底面积为512,平行于底面的截面面积为50,则截得的棱台的高为__________________.16.如图是一个组合几何体的三视图,则该几何体的体积是__________________.三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤) 17.(10分)把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:4,母线长为10cm .求圆锥的母线长.18.(12分)如图是一个几何体的正视图和俯视图. (1)试判断该几何体是什么几何体?(2)画出其侧视图,并求该平面图形的面积;(3)求出该几何体的体积.19.(12分)如下图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由. 20.(12分)已知某几何体的侧视图与其正视图相同,相关的尺寸如图所示,求这个几何体的体积.21.(12分)如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,7m,制造这个塔顶需要多少铁板?(2)三棱锥A′-BC′D的体积.22.(12分)如图,正方体ABCD-A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:(1)三棱锥A′-BC′D的表面积与正方体表面积的比值;2018-2019学年必修二第一章训练卷空间几何体(一)答 案一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的) 1.【答案】D【解析】由几何体的三视图可得,该几何体为四棱台.故选D. 2.【答案】D【解析】△OAB 是直角三角形,OA =6,OB =4,∠AOB =90°,∴164122OAB S =⨯⨯=△.故选D .3.【答案】A【解析】由菱形的对角线长分别是9和15,得菱形的边长为22915334222⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭,则这个菱柱的侧面积为3434530342⨯⨯=.故选A . 4.【答案】A【解析】依题意,得圆锥的底面周长为πR ,母线长为R ,则底面半径为2R,高为32R ,所以圆锥的体积2313332224R R R ⎛⎫⨯π⨯⨯=π ⎪⎝⎭.故选A . 5.【答案】D【解析】()121::3:13V V Sh Sh ⎛⎫== ⎪⎝⎭.故选D .6.【答案】B【解析】设球半径是R ,依题意知,该三棱柱是一个底面边长为2,侧棱长为1的正三棱柱,记上,下底面的中心分别是O 1,O ,易知球心是线段O 1O 的中点,于是222123192312R ⎛⎫⎛⎫=+= ⎪ ⎪ ⎪⎝⎭⎝⎭,因此所求球的表面积是2191944123R ππ=π⨯=, 故选B. 7.【答案】C【解析】设正方体的棱长为a,则a 3=8,所以a =2,而此正方体内的球直径为2,所以S表=4πr 2=4π.故选C.8.【答案】C【解析】该几何体的直观图为如图所示的四棱锥P -ABCD ,且P A =AB =AD =1,P A⊥AB ,P A ⊥AD ,四边形ABCD 为正方形,则2111133V =⨯⨯=,故选C.9.【答案】B【解析】设圆锥底面半径为r ,则12384r ⨯⨯=,∴163r =,所以米堆的体积为21116320354339⎛⎫⨯⨯⨯⨯= ⎪⎝⎭,故堆放的米约为320 1.62229÷≈,故选B. 10.【答案】B【解析】由题意知棱柱的高为23cm ,底面正三角形的内切圆的半径为3cm ,∴底面正三角形的边长为6cm ,正三棱柱的底面面积为293cm ,∴此三棱柱的体积()3932354cm V =⨯=.故选B.11.【答案】C【解析】由零件的三视图可知,该几何体为两个圆柱组合而成,如图所示.切削掉部分的体积V 1=π×32×6-π×22×4-π×32×2=20π(cm 3), 原来毛坯体积V 2=π×32×6=54π(cm 3).故所求比值为1220105427V V π==π.故选C. 12.【答案】A【解析】设球的半径为R ,则由题知球被正方体上面截得圆的半径为4, 球心到截面圆的距离为R -2,则R 2=(R -2)2+42,解得R =5.∴球的体积为3345500cm33π⨯π=.故选A.二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.【答案】①②③⑤【解析】三棱锥的三视图中含有三角形,∴正视图有可能是三角形,满足条件.四棱锥的三视图中含有三角形,满足条件.三棱柱的三视图中含有三角形,满足条件.四棱柱的三视图中都为四边形,不满足条件.圆锥的三视图中含有三角形,满足条件.圆柱的三视图中不含有三角形,不满足条件.故答案为①②③⑤.14.【答案】6 415.【答案】11【解析】设棱台的高为x,则有2165016512x-⎛⎫=⎪⎝⎭,解之,得x=11.16.【答案】36+128π【解析】由三视图可知该组合几何体下面是一个圆柱,上面是一个三棱柱,故所求体积为134616836128 2V=⨯⨯⨯+π⨯=+π.三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤)17.【答案】403cm.【解析】如图,设圆锥母线长为l,则1014ll-=,所以cm403l=.18.【答案】(1)正六棱锥;(2)见解析,232a;(3)332a.【解析】(1)由该几何体的正视图和俯视图可知该几何体是一个正六棱锥.(2)该几何体的侧视图如图.其中AB=AC,AD⊥BC,且BC的长是俯视图正六边形对边的距离,即3BC a=,AD是正六棱锥的高,即3AD a,所以该平面图形的面积为2133322a a a=.(3)设这个正六棱锥的底面积是S,体积为V,则223336S==,所以231333332V a a==.19.【答案】不会,见解析.【解析】因为()33314144134cm2323V R=⨯π=⨯⨯π⨯≈半球,()22311412201cm33V r h=π=π⨯⨯≈圆锥,134<201,所以V半球<V圆锥,所以,冰淇淋融化了,不会溢出杯子.20.【答案】74Vπ=.【解析】由三视图可知,该几何体是大圆柱内挖掉了小圆柱,两个圆柱高均为1,底面是半径为2和32的同心圆,故该几何体的体积为23741124Vπ⎛⎫=π⨯-π⨯=⎪⎝⎭.21.【答案】282m .【解析】如图所示,连接AC 和BD 交于O ,连接SO .作SP ⊥AB ,连接OP .在Rt △SOP 中,)7m SO =,()11m 2OP BC ==,所以)22m SP =, 则△SAB 的面积是)2122222m 2⨯⨯.所以四棱锥的侧面积是)242282m ⨯=,即制造这个塔顶需要282铁板.22.【答案】3;(2)33a .【解析】(1)∵ABCD -A ′B ′C ′D ′是正方体, ∴2A B A C A D BC BD C D a ''''''======,∴三棱锥A ′-BC ′D 的表面积为213422232a a a ⨯=.而正方体的表面积为6a 2,故三棱锥A ′-BC ′D 的表面积与正方体表面积的比值为2233a =. (2)三棱锥A ′-ABD ,C ′-BCD ,D -A ′D ′C ′,B -A ′B ′C ′是完全一样的.故V 三棱锥A ′-BC ′D =V 正方体-4V 三棱锥A ′-ABD =332114323a a a a -⨯⨯⨯=.。
高中数学必修2(人教A版)第一章几何空间体1.1知识点总结含同步练习及答案

描述:例题:描述:高中数学必修2(人教A版)知识点总结含同步练习题及答案第一章 空间几何体 1.1 空间几何体的结构一、学习任务认识柱、锥、台、球及其简单组合体的结构特征,能运用这些结构特征描述现实生活中简单物体的结构.二、知识清单典型空间几何体空间几何体的结构特征 组合体展开图 截面分析三、知识讲解1.典型空间几何体空间几何体的概念只考虑物体的形状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.2.空间几何体的结构特征多面体由若干个平面多边形围成的几何体叫做多面体.围成多面体的各个多边形叫做多面体的面;相邻两个面的公共边叫做多面体的棱;棱与棱的公共点叫做多面体的顶点;连接不在同一个面上的两个顶点的线段叫做多面体的对角线.按多面体的面数可把多面体分为四面体、五面体、六面体.其中,四个面均为全等的正三角形的四面体叫做正四面体.旋转体由一个平面图形绕它所在的平面内的一条定直线旋转所形成的封闭几何体叫做旋转体.这条定直线叫做旋转体的轴.棱柱的结构特征一般地,有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱(prism).棱柱中,两个互相平行的面叫做底面,简称底;其余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧棱与底面的公共顶点叫做棱柱的用一个平行于棱锥底面的平面去截棱锥,得到两个几何体,一个是______,另一个是______.解:棱锥;棱台.⋯⋯余各面叫做棱柱的侧面;相邻侧面的公共边叫做棱柱的侧棱;侧棱与底面的公共顶点叫做棱柱的顶点.底面是三角形、四边形、五边形的棱柱分别叫做三棱柱、四棱柱、五棱柱,可以用表示底面各顶点的字母或一条对角线端点的字母表示棱柱,如下图的六棱柱可以表示为棱柱或棱柱 .侧棱与底面不垂直的棱柱叫做斜棱柱;侧棱与底面垂直的棱柱叫做直棱柱;底面是正多边形的直棱柱叫做正棱柱;底面是平行四边形的棱柱叫做平行六面体;侧棱与底面垂直的平行六面体叫做直平行六面体.棱锥的结构特征一般地,有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥(pyramid).这个多边形面叫做棱锥的底面或底;有公共顶点的各个三角形面叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点;相邻侧面的公共边叫做棱锥的侧棱.底面是三角形、四边形、五边形的棱锥分别叫做三棱锥、四棱锥、五棱锥其中三棱锥又叫四面体.棱锥也用表示顶点和底面各顶点的字母或者用表示顶点和底面一条对角线端点的字母来表示,如下图的四棱锥表示为棱锥 或者棱锥 .棱锥的底面是正多边形,且它的顶点在过底面中心且与底面垂直的直线上,这个棱锥叫做正棱锥.正棱锥各侧面都是全等的等腰三角形,这些等腰三角形底边上的高都相等,叫做棱锥的斜高.⋯⋯⋯⋯ABCDEF−A′B′C′D′E′F′DA′⋯⋯⋯⋯S−ABCD S−AC棱台的结构特征用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分,这样的多面体叫做棱台(frustum of a pyramid).原棱锥的底面和截面分别叫做棱台的下底面和上底面;其他各面叫做棱台的侧面;相邻两侧面的公共边叫做棱台的侧棱;两底面的距离叫做棱台的高.由正棱锥截得的棱台叫做正棱台,正棱台的各个侧面都是全等的等腰梯形,这些等腰梯形的高叫做棱台的斜高.圆柱的结构特征以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱(circular cylinder).旋转轴叫做圆柱的轴;垂直于轴的边旋转而成的圆面叫做圆柱的底面;平行于轴的边旋转而成的曲面叫做圆柱的侧面;无论旋转到什么位置,不垂直于轴的边都叫做圆柱侧面的母线.圆锥的结构特征以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥(circular cone).圆台的结构特征例题:用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台(frustum of a cone).棱台与圆台统称为台体.球的结构特征以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球(solid sphere).半圆的圆心叫做球的球心,半圆的半径叫做球的半径,半圆的直径叫做球的直径.球常用表示球心的字母 表示.O下列命题中,正确的是( )A.有两个面互相平行,其余各面都是四边形的几何体叫棱柱B.棱柱中互相平行的两个面叫做棱柱的底面C.棱柱的侧面是平行四边形,而底面不是平行四边形D.棱柱的侧棱长相等,侧面是平行四边形解:D如图(1),满足 A 选项条件,但不是棱柱;对于 B 选项,如图(2),构造四棱柱,令四边形 是梯形,可知 ,但这两个面不能作为棱柱的底面;C选项中,若棱柱是平行六面体,则它的底面是平行四边形.ABCD−A1B1C1D1ABCD面AB∥面DCB1A1C1D1若正棱锥的底面边长与侧棱长相等,则该棱锥一定不是( )A.三棱锥 B.四棱锥 C.五棱锥 D.六棱锥解:D如下图,正六边形 中,,那么正六棱锥中,,即侧棱长大于底面边长.ABCDEF OA=OB=⋯=AB S−ABCDEF SA>OA=AB描述:3.组合体简单组合体的构成有两种基本形式:一种是由简单几何体拼接而成,一种是由简单几何体截去或挖去一部分而成.如图所示的几何体中,是台体的是( )A.①② B.①③ C.③ D.②③解:C利用棱台的定义求解.①中各侧棱的延长线不能交于一点;②中的截面不平行于底面;③中各侧棱的延长线能交于一点且截面与底面平行.有下列四种说法:①圆柱是将矩形旋转一周所得的几何体;②以直角三角形的一直角边为旋转轴,旋转所得几何体是圆锥;③圆台的任意两条母线的延长线,可能相交也可能不相交;④半圆绕其直径所在直线旋转一周形成球.其中错误的有( )A.个 B. 个 C. 个 D. 个解:D圆柱是矩形绕其一条边所在直线旋转形成的几何体,故①错;以直角三角形的一条直角边所在直线为轴,旋转一周,才能构成圆锥,②错;圆台是由圆锥截得,故其任意两条母线延长后一定交于一点,③错;半圆绕其直径所在直线旋转一周形成的是球面,故④错误.1234例题:描述:4.展开图空间形体的表面在平面上摊平后得到的图形,是画法几何研究的一项内容.描述图中几何体的结构特征.解:图(1)所示的几何体是由两个圆台拼接而成的组合体;图(2)所示的几何体是由一个圆台挖去一个圆锥得到的组合体;图(3)所示的几何体是在一个圆柱中间挖去一个三棱柱后得到的组合体.下图中的几何体是由哪个平面图形旋转得到的( )解:D)不在同一平面内的有______对.3内.解:C描述:例题:5.截面分析截面用平面截立体图形所得的封闭平面几何图形称为截面.平行截面、中截面与立体图形底面平行的截面称为平行截面,等分立体图形的高的平行截面称为中截面.轴截面包含立体图形的轴线的截面称为轴截面.球截面球的截面称为球截面.球的任意截面都是圆,其中通过球心的截面称为球的大圆,不过球心的截面称为球的小圆.球心与球的截面的圆心连线垂直于截面,并且有 ,其中 为球的半径, 为截面圆的半径, 为球心到截面的距离.+=r 2d 2R 2R r d 下面几何体的截面一定是圆面的是( )A.圆台 B.球 C.圆柱 D.棱柱解:B如图所示,是一个三棱台 ,试用两个平面把这个三棱台分成三部分,使每一部分都是一个三棱锥.解:如图,过 ,, 三点作一个平面,再过 ,, 作一个平面,就把三棱台分成三部分,形成的三个三棱锥分别是 ,,.ABC −A ′B ′C ′A ′B C A ′B C ′ABC −A ′B ′C ′−ABC A ′−B B ′A ′C ′−BC A ′C ′如图,正方体 中,,, 分别是 ,, 的中点,那么正方体中过点 ,, 的截面形状是( )A.三角形 B.四边形 C.五边形 D.六边形ABCD −A 1B 1C 1D 1P Q R AB AD B 1C 1P QR作截面图如图所示,可知是六边形.ii)若两平行截面在球心的两侧,如图(2)所示,则 解:四、课后作业 (查看更多本章节同步练习题,请到快乐学)答案:1.如图,能推断这个几何体可能是三棱台的是 .A .B .C .D .C ()=2,AB =3,=3,BC =4A 1B 1B 1C 1=1,AB =2,=1.5,BC =3,=2,AC =3A 1B 1B 1C 1A 1C 1=1,AB =2,=1.5,BC =3,=2,AC =4A 1B 1B 1C 1A 1C 1AB =,BC =,CA =A 1B 1B 1C 1C 1A 1答案:2. 纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北.现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到如图所示的平面图形,则标" "的面的方位是 .A .南B .北C .西D .下B △()3. 向高为 的水瓶中注水,注满为止,如果注水量 与水深 的函数关系的图象如图所示,那么水瓶的形状是.A .H V h ()高考不提分,赔付1万元,关注快乐学了解详情。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.....
13、从长方体的一个极点出发的三条棱上各取一点E、F、G,过此三点作长方体的截面,那
么截去的几何体是_________.
14、一个圆柱和一个圆锥的母线相等,底面半径也相等,则侧面积之比是_________.
三、解答题(本大题共6小题,15、16、17、18每题13分,19、20每题14分,共80分)
,则球的表面积是
(
)
A.8
cm2
B.12
cm2
C.16
cm
2
D.20
cm2
9、一个正方体的极点都在球面上,此球与正方体的表面积之比是()
A.
B.
C.
D.
3
4
2
10、如右图为一个几何体的三视图
,此中府视图为正三角形
,A1B1=2,AA1=4,则该几何体
C1
的表面积为 (
)
A1
B1
A. 6+
3
B. 24+
积为()
A.6a2B.6a2C.3a2D.3a2
22
4、已知圆柱与圆锥的底面积相等,高也相等 ,它们的体积分别为V1和V2,则V1:V2是:
()
A.1:3B.1:1C.2:1D.3:1
5、假如两个球的体积之比为8:27,那么两个球的表面积之比为()
A.8:27B. 2:3C.4:9D. 2:9
6、 有一个几何体的三视图及其尺寸以下(单位cm), 长度之和为24,求长方体的对角线的长。
.专业word可编写.
.....
19.已知一个半径为
3的球有一个内接正方体
(几正方体的极点都在球面上
), 求这个球
的球面面积与其内接正方体的全面积之比。
20.如图是从上下底面处在水平状态下的棱长为
a的正方体ABCD-A1B1C1D1中分别出来的。
(1)
DC1D1在图中的度数和它表示的角的真切度数都是45
,对吗?
D
C
B
D1
C1
A1
B1
(2
)
A1C1D的真切度数是
60,对吗?
(3
)设BC=1,假如用图示中这样一个装置来盛水
,那么最多能盛多少体
积的水 ?
.专业word可编写.
.....
参照答案
1.A;2.B;3.A;4.D;5.C;6.A;7.C;8.B;9.C;10.C.
()
.专业word可编写.
.....
5
6
A. 24πcm2,12πcm3
B. 15πcm2,12
πcm3
C. 24πcm2,36πcm3
D.以上都不正确
7、一个球的外切正方体的表面积等于
6 cm2,则此球的体积为 (
)
A.4
cm3
B.6
cm3
C.
1
cm
3
D.
6
cm3
3
8
6
6
8、一个体积为8cm3
的正方体的极点都在球面上
10Q
11.15;12.
;13.
三棱锥 ;14.2:1
9
15.解:l=3,R=1;S=4
2
2
;V=
.
3
16.R=1,h=
3,S=2
+2
3.
17.S=60
+42;V=52
8
148
.
-
=
33
18.5
19..
2
20.(1)对.
(2)对.
1
(3)
6
.专业word可编写.
.....
.专业word可编写.
.....
高二数学必修二第一章测试题
一、选择题(本大题共10小题,每题5分,共50分)
1、 图(1)是由哪个平面图形旋转获得的()
ABCD
2、过圆锥的高的三平分点作平行于底面的截面,它们把圆锥侧面分红的三部分的面积之比
()
A.1:2:3B.1:3:5C.1:2:4D.1:3:9
3、已知水平搁置的ABC的平面直观图A B C是边长为a的正三角形 ,那么ABC的面
3
C. 24+2
3
D. 32
AC
B
正视图
侧视图
府视图
一、选择题答题表
题号12345678910
答案
二、填空题(本大题共4小题,每题5分,共20分)
11.长方体的共极点的三个侧面面积分别为3,5,15,则它的体积为_______________.
12.一个半球的全面积为Q,一个圆柱与此半球等底等体积 ,则这个圆柱的全面积是.
15.将圆心角为1200,面积为3的扇形 ,作为圆锥的侧面,求圆锥的表面积和体积.
16.(如图)在底半径为2母线长为4的圆锥中内接一个高为3的圆柱 ,求圆柱
的表面积
17、如图,在四边形ABCD中,,,,,
AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
.专业word可编写.
.....
