Buck直流变换器的工作原理及动态建模
Buck-Boost电路建模及分析

题目:Buck-Boost电路建模及分析摘要:作为研究开关电源的基础,DC-DC开关变换器的建模分析对优化开关电源的性能和提高设计效率具有重要意义。
而Buck-Boost电路作为DC-DC开关变换器的其中一种电路拓扑形式,因其输出电压极性与输入电压相反,而幅度既可比输入电压高,也可比输入电压低,且电路结构简单而流行。
为了达到全面而深入的研究效果,本文对Buck-Boost电路进行了稳态分析和小信号分析。
稳态分析中,首先介绍了电路工作原理,得出了两种工作模式下的电压转换关系式,并同时可知基于占空比怎样计算其输出电压以及最小最大电感电流和输出纹波电压计算公式;接着推导了状态空间模型,以在MATLAB中进行仿真;而最后仿真得到的电感电流、输出电压的变化规律符合理论分析。
小信号分析中,首先推导了输出与输入间的传递函数表达式,以了解低频交流小信号分量在电路中的传递过程;接着分析其零极点,且仿真绘制波特图进行了验证。
经过推导与研究,稳态分析和小信号分析下仿真得到的变化规律均与理论上的推导一致。
关键词:Buck-Boost;稳态分析;小信号分析;MATLAB仿真1.概论现代开关电源有两种:直流开关电源、交流开关电源。
本课题主要介绍直流开关电源,其功能是将电能质量较差的原生态电源,如市电电源或蓄电池电源,转换为满足设备要求的质量较高的直流电源,即将“粗电”转换为“精电”。
直流开关电源的核心是DC-DC变换器。
作为研究开关电源的基础,DC-DC开关变换器的建模分析对开关电源的分析和设计具有重要意义。
DC-DC开关变换器最常见的三种电路拓扑形式为:降压(Buck)、升压(Boost)和降压-升压(Buck-Boost) [1],如图1-1所示。
其中Buck-Boost变换器因其输出电压极性与输入电压相反,而幅度既可比输入电压高,也可比输入电压低,且电路结构简单而流行。
(a) Buck型电路结构(b) Boost型电路结构(c) Buck-Boost型电路结构图1-1 DC-DC变换器的三种电路结构本课题针对Buck-Boost变换器的建模分析进行深入研究,以优化开关电源的性能和提高设计效率。
buck-boost变换器工作原理

buck-boost变换器工作原理
Buck-boost变换器是一种电力转换装置,它可以将直流电压转换为不同的电压水平,从而实现电源的调整和控制。
它工作的原理基于开关电源的工作原理和能量储存原理。
Buck-boost变换器的基本结构包括开关管、电感、电容和控制电路。
工作原理如下:
1. 当输入电压高于输出电压时,开关管K1关闭,开关管K2打开。
此时,电感L和电容C组成的LC滤波回路开始储存能量。
电感L的磁场储存了电流的能量,电容C储存了电压的能量。
2. 在上述状态下,当开关管K1关闭时,由于电感的特性,电流不会突变。
电感L会释放储存的能量,电流会从电感流向负载。
3. 当电感释放能量时,负载上的电压会高于输入电压。
这样就实现了电压升高的功能。
4. 当输入电压低于输出电压时,开关管K1打开,开关管K2关闭。
此时,电容C充满了能量,而电感L则储存能量。
5. 在上述状态下,当开关管K1打开时,电感的磁场会继续储存能量。
电感释放能量,电流从电感流向负载。
6. 当电感释放能量时,负载上的电压会低于输入电压。
这样就实现了电压降低的功能。
通过不断地开关开关管K1和K2,Buck-boost变换器可以实现输入电压到输出电压的转换。
控制电路会根据输出电压的变化来控制开关管的状态,以实现稳定的输出电压。
总结起来,Buck-boost变换器通过周期性地储存和释放能量来实现对输入电压的调节,从而实现对输出电压的升高或降低。
这种转换过程是通过改变开关管的状态来控制的,通过控制电路实现对输出电压的稳定性控制。
Buck变换器建模和仿真
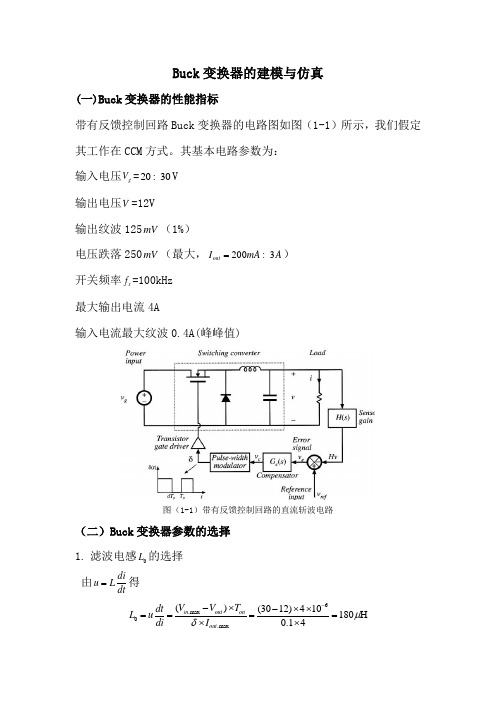
Buck 变换器的建模与仿真(一)Buck 变换器的性能指标带有反馈控制回路Buck 变换器的电路图如图(1-1)所示,我们假定其工作在CCM 方式。
其基本电路参数为: 输入电压g V =2030V 输出电压V =12V 输出纹波125mV (1%)电压跌落250mV (最大,2003out I mA A =) 开关频率s f =100kHz 最大输出电流4A输入电流最大纹波0.4A(峰峰值)图(1-1)带有反馈控制回路的直流斩波电路(二)Buck 变换器参数的选择 1. 滤波电感0L 的选择 由diu Ldt=得 6.max 0.max ()(3012)410180H 0.14in out on out V V T dt L u di I μδ--⨯-⨯⨯====⨯⨯这里我们取0L 为180H μ 最大负载时的峰值电流为.max .max 40.054 4.22peak out out I I I A δ=+=+⨯=2. 滤波电容0C 的选择 由dui cdt=得 其向量形式为I j cU ω=I jcUω=所以需要穿越频率的带宽为2outc out outI f C V π∆=∆如果假定穿越频率为10kHz250892.8out c out V mZ m I ∆===Ω∆ 原则上为了留有设计裕量,电阻的阻抗按13计算阻抗选取 根据上面计算结果,我们可以在Rubycon 公司的ZL 系列,16V 中选取以下规格:C=330F μ,760C rms I mA =@105A C =︒ ,72ESR low R m =Ω@20A T C =︒ ,220ESR low R m =Ω@10A T C =-︒电容ESR 的阻抗应小于输出电容在穿越频率处的阻抗11482 6.2810330c out m f C k π==Ω⨯⨯86c Z m ≤==Ω设计余量不足,我们重新选ZL 系列中C=1000F μ,同样的过程,我们可以得出满足条件。
Buck降压式变换器基本结构及原理

Buck降压式变换器基本结构及原理一、Buck变换器:也称降压式变换器,是一种输出电压小丁输入电压的单管不隔离直流变换器。
图中,Q为开关管,其驱动电压一般为PWM(Pulse width modulation脉宽调制)信号,信号周期为Ts ,则信号频率为f=1/Ts ,导通时间为Ton,关断时间为Toff,则周期Ts=Ton+Toff ,占空比Dy= Ton/Ts。
Buck变换器有两种基本工作方式:CCM(Continuous current mode) :电感电流连续模式,输出滤波电感Lf的电流总是大丁零DCM(Discontinuous current mode) :电感电流断续模式,在开关管关断期间有一段时间Lf的电流为零1.1 CCM时的基本关系:0.5 1-0 g 050 L0V tlt= corist V0 = const1.3.11.2 DCM 时的基本关系:% %输出电压与输人电反间的关系:曜== 七一 4劣十口 其中:AD <(1 一心)为美断后电感电流下降到零的时问J =气;% 乙狄011 1,小,V 七 输出平均曲克:二〒七+ T0二司土~ W 〔气*& £ 顷心 J在电勰喽时,%附不但与占空比Dy 有关』而且与或载电流卜大小有关,若1口=0,则%=甲血 DCM 可分为两种典型情况:输入电压Vin 不变,输出电压Vo 变化,常用作电动机速度控 制或充电器对蓄电池的包流充电输入电压Vin 变化,输出电压Vo 包定,即普通开关稳压电源1.3 电感电流临界连续的边界:用f g 表示临界电流通彼阿的负更电疏】Q ,则:; 鱼w 吃眼w (D* 头h ' 头L 叫史输入电压包定不变时:Vin=const临界负载电流是大值在Dy=0 5时出现: 皿】如=4—球(1-巳)劣电添临界连续时前输出电压:争= ------------ \ --------顷 一 - + 140; ^O (?HMX可画出Buck 变换器在Vin=const 时的外特性曲线:输出走压与情人电压间的关策:竺=一-—。
同步Buck变换器动态解析

同步Buck变换器动态解析1 概述相对于传统的线性电源,开关电源具有转换效率高、输入电压范围大、输出电压稳定等优点,广泛应用于工业控制、电力系统等领域。
开关电源的拓扑形式多种多样,其中Buck变换器是最为简单且具代表的一种,已应用于光伏并网、LED和电池充电等领域。
虽然Buck变换器应用广泛,但其分析过程大部分是基于微分方程的,分析过程欠直观,难于工程应用。
相平面法是分析非线性系统的一种常用方法,通过相平面图直观清晰地反映系统的动态过程及性能,其计算简单、概念清晰,非常适合于工程应用。
本文利用相平面法对同步Buck变换器的动态过程进行分析,选取具体的物理量为相平面坐标轴,通过相平面得到Buck变换器中变量的变化趋势,为后续的分析设计提供依据。
2 同步Buck变换器模型Buck变换器的原理图如下:当开关S1、S2处于不同状态时,该电路有不同的动态特性,该系统属于切换系统,其数学模型如下:当S1闭合、S2断开时,Buck变换器的状态空间模型如下:当S1断开、S2闭合时,Buck变换器的状态空间模型如下:式(1)、式(2)中:L表示电感感量;C表示输出电容容量;R表示负载电阻阻值;iL表示电感电流;vi表示输入电压;vo表示输出电压。
当电路正常工作时,以上两种状态不停切换,其整体呈现出来的动态特性就是以上两种特性的叠加。
3 Buck变换器的相平面模型及其动态分析若对同步Buck变换器直接套用传统的相平面法,则获得输出电压及其导数构成的相平面,与实际物理量不存在直接对应的关系。
为了获得物理意义明确的相平面图,这里选择实际物理量作为相平面坐标,使相平面更加直观清晰。
对上述的同步Buck模型,选取vo为横坐标、iL为纵坐标,则相平面中的曲线斜率如下:当S1闭合、S2断开时,相平面中的斜率为:当S1断开、S2闭合时,相平面中的斜率为:根据以上式(3)和式(4),对vi=12V、L=5uH、C=22uF,R=1Ω的同步Buck变换器进行计算,得到以下相平面曲线:当S1闭合、S2断开时,vo和iL会沿着图2中“o-”的方向顺时针变化,其运动轨迹如图3实线所示;当S1断开、S2闭合时,vo和iL会沿着图2中“*-”的方向顺时针变化,其运动轨迹如图3虚线所示。
Buck变换器的结构及工作原理

Buck变换器的结构及工作原理高压水射流清洗技术是近年来在国际上兴起的一门高科技清洗技术,具有清洗速度快、效率高、成本低、清洁环保、不腐蚀损伤基体、适用范围广、易于实现自动化和智能化控制等优点,可清洗形状结构复杂的零部件[1]。
近年来,随着自动控制技术的不断发展,工业自动化水平日益提高。
为了提高高压水射流设备的清洗效率和清洗效果,有研究人员将自动控制技术运用到射流清洗过程中。
其清洗效果和清洗效率相对于传统的人工清洗有了很大的提升,但该过程对于控制系统的实时性、稳定性具有较高的要求。
因而作为控制系统的驱动部分,直流电源输出的快速性、稳定性也有较高的要求。
传统的驱动电源多以线性直流稳压电源为主,由于电压调整功能的器件始终工作于线性放大区,因而在应用过程中存在着功耗大、能量转换效率低、输出响应速度慢等问题。
这为线性直流电源的应用带来了很大的局限性。
近年来,随着电力电子功率器件的不断发展,开关电源得到了越来越广泛的应用,其相关的技术及发展现状如文献[2]所述。
开关电源具有较多的优点。
如内部功率损耗小、转换效率高。
随着超高频功率变换技术[3]的不断发展与应用,开关电源的转换效率可以大幅度提高,其转换效率可高达90%以上,即达到文献[4]所述合理使用能源、减少能量损耗的目的。
而且开关电源由于没有传统的工频变压器,散热器相对较小,因而具有体积小、重量轻的特点。
开关电源不仅具有以上所说的优点,与其相应的电路的控制方法也比较多,如循环控制方法[5]、滞环控制方法[6]、移相控制方法[7]等。
设计人员可以根据实际应用的要求和需要,灵活地选用各种类型的开关电源电路和控制方法。
本文针对传统线性直流稳压电源与开关直流电源的以上特点,结合射流清洗设备的触摸屏驱动电源输入输出响应要求。
设计了一种基于传统线性直流电源电路的开关电源电路结构,文中首先给出了相应的电路结构,并对相应的工作原理做了简要说明,其次给出了仿真结构图的搭建方法及结果分析,最后给出了所得结论。
Buck直流变换器的工作原理及动态建模

2 Buck 直流变换器的工作原理及动态建模DC/DC 变换器的概念7【】15【】19【】将一个固定的直流电压变换成可变的直流电压称之为DC/DC 变换,亦称为直流斩波。
用斩波器斩切直流的基本思想是:如果改变开关的动作频率,或者改变直流电流通和断的时间比例,就可以改变加到负载上的电压、电流的平均值。
Buck 变换器又称降压变换器、串连开关稳压电源、三端开关型降压稳压器。
基本的DC/DC 变换器按输入输出之间是否有电气隔离可分为两类:隔离型DC/DC 变换器和非隔离型DC/DC 变换器。
非隔离型DC/DC 变换器中存在四种基本的变换器拓扑,它们是降压式(Buck )型,升压式(Boost)型,升降压式(Buck-boost)型,Cuk 型,此外还有Sepic 型和Zeta 型变换器。
二电平Buck 直流变换器的工作原理及主电路图2【】13【】25【】26【】1 主电路拓扑Buck 变换器是一种输出电压等于或小于输入电压的单管非隔离直流变换器。
它的拓扑为电压源、串联开关和电流负载组合而成。
如图所示:图 Buck 电路主电路拓扑为了分析稳态特性,简化推导公式的过程,特作如下假定。
(1) 开关晶体管、二极管均是理想元件。
也就是可以瞬间的导通和截至,而且导通时降压为零,截至时漏电流为零。
(2) 电感、电容是理想元件。
电感工作在线性区而未饱和,寄生电阻为零,电容的等效串联电阻为零。
(3) 输出电压中的纹波电压与输出电压的比值小到允许忽略。
Buck 变换器的工作原理:当开关管S 导通时,电容开始充电,i U 通过向负载传递能量,此时,L i 增加,电感内的电流逐渐增加,储存的磁场能量也逐渐增加,而续流二极管因反向偏置而截至;当S 关断时,由于电感电流L i 不能突变,故L i 通过二极管VD 续流,电感电流逐渐减小,由于二极管VD 的单向导电性,L i 不可能为负,即总有L 0i ,从而可在负载上获得单极性的输出电压。
开关电源 之BUCK变换器工作原理及Multisim实例仿真
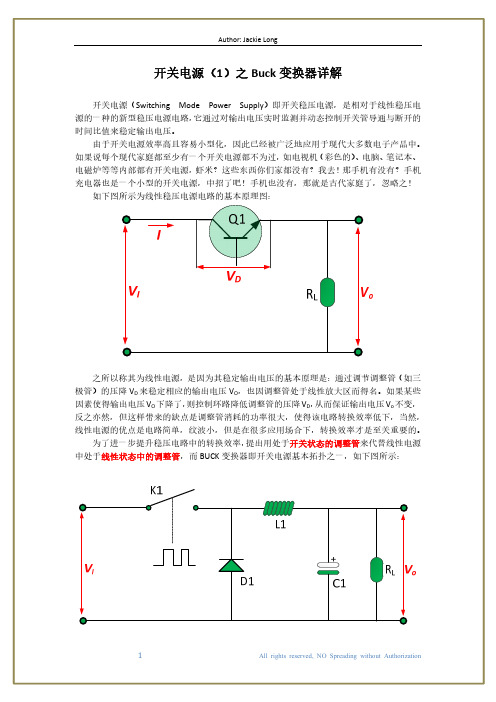
D1 1N5824
A PR1
PR3
V
3
V: 5.71 V V(p-p): 29.3 mV V(rms): 5.73 V V(dc): 5.70 V V(f req): 22.3 kHz
C1
R1
22பைடு நூலகம்µF
5Ω
根据上图仿真结果,则有:
1.14 5.7 0.58 12
93.36%
其中,开关 K1 代表三极管或 MOS 管之类的开关管(本文以 MOS 管为例),通过矩形波 控制开关 K1 只工作于截止状态(开关断开)或导通状态(开关闭合),理想情况下,这两种 状态下开关管都不会有功率损耗,因此,相对于线性电源的转换效率有很大的提升。
开关电源调压的基本原理即面积等效原理,亦即冲量相等而形状不同的脉冲加在具有惯 性环节上时其效果基本相同,如下图所示:
理想的 MOS 管在工作时(即导通或截止)的压降及流过其中的电流应如下图所示:
9
All rights reserved, NO Spreading without Authorization
DS
Author: Jackie Long
D
其中,VDS 表示 MOS 管两端的压降,而 ID 表示流经 MOS 管的电流,在任意时刻,VDS 与 ID 都会有一个参数为 0,因此消耗的功率 P=U×I 也应当是 0,但是实际 MOS 管的开关与 闭合都是需要过渡时间的,真实的开/关状态如下图所示:
同样是从输入电源 10V 中获取 5V 的输出电压,线性稳压电源的有效面积为 5×T,而对 应在开关稳压电源的单个有效周期内,其有效面积为 10×T×50%(占空比)=5×T,这样只要 在后面加一级滤波电路,两者的输出电压有效值(平均值)是相似的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 Buck 直流变换器的工作原理及动态建模DC/DC 变换器的概念7【】15【】19【】将一个固定的直流电压变换成可变的直流电压称之为DC/DC 变换,亦称为直流斩波。
用斩波器斩切直流的基本思想是:如果改变开关的动作频率,或者改变直流电流通和断的时间比例,就可以改变加到负载上的电压、电流的平均值。
Buck 变换器又称降压变换器、串连开关稳压电源、三端开关型降压稳压器。
基本的DC/DC 变换器按输入输出之间是否有电气隔离可分为两类:隔离型DC/DC 变换器和非隔离型DC/DC 变换器。
非隔离型DC/DC 变换器中存在四种基本的变换器拓扑,它们是降压式(Buck )型,升压式(Boost)型,升降压式(Buck-boost)型,Cuk 型,此外还有Sepic 型和Zeta 型变换器。
二电平Buck 直流变换器的工作原理及主电路图2【】13【】25【】26【】1 主电路拓扑Buck 变换器是一种输出电压等于或小于输入电压的单管非隔离直流变换器。
它的拓扑为电压源、串联开关和电流负载组合而成。
如图所示:图 Buck 电路主电路拓扑为了分析稳态特性,简化推导公式的过程,特作如下假定。
(1) 开关晶体管、二极管均是理想元件。
也就是可以瞬间的导通和截至,而且导通时降压为零,截至时漏电流为零。
(2) 电感、电容是理想元件。
电感工作在线性区而未饱和,寄生电阻为零,电容的等效串联电阻为零。
(3) 输出电压中的纹波电压与输出电压的比值小到允许忽略。
Buck 变换器的工作原理:当开关管S 导通时,电容开始充电,i U 通过向负载传递能量,此时,L i 增加,电感内的电流逐渐增加,储存的磁场能量也逐渐增加,而续流二极管因反向偏置而截至;当S 关断时,由于电感电流L i 不能突变,故L i 通过二极管VD 续流,电感电流逐渐减小,由于二极管VD 的单向导电性,L i 不可能为负,即总有L 0i ,从而可在负载上获得单极性的输出电压。
根据晶体管的开关特性,在管子的基极加入开关信号,就能控制它的导通和截至,对于NPN 晶体管,当基极加入正向信号时,将产生积极电流b i ,基极正向电压电压升高,b i 也随之升高,b i 达到一定数值后,集电极电流c i 达到最大值,其后继续增加b i ,b i 基本上保持不变,这种现象称为饱和。
在饱和状态下,晶体管的集射极电压很小,可以忽略不计。
因此晶体管的饱和状态相当于开关的接通状态。
当基极加入反向偏压时,晶体管截至,集电极电流c i 接近于零,而晶体管的集射极电压接近于电源电压。
晶体管的这种状态相当于开关的断开状态,通常称为截至状态,或称为关断状态。
Buck 变换器的工作模式5【】8【】27【】29【】由Buck 变换器的工作原理可以看出,电感可以工作在电流连续的方式下,也可能工作在电流不连续的工作状态。
以此为标准将Buck 变换器的工作模式分为两种:电感电流连续工作模式(continuous current mode, CCM)和电感电流断续模式(discontinuous current mode, DCM)。
电感电流连续是指输出滤波电感的电流总大于零,电感电流断续是指在快关管段期间有一段时间输出滤波的电流为零。
在这种工作方式之间有一个工作边界,称为电感电流临界连续状态,即在开关管关断末期,滤波电感的电流刚好降为零。
下面分别讨论电感电流处于不同模式时的变换器工作原理。
(1) 电感电流连续模式如图所示为电流连续导电模式下的相关波形:图 电流连续模式下电路波形在[]10t 区间,开关管S 处于导通状态,电源电压通过S 到二极管VD 两端,故二极管VD 截至。
电流流过电感,由于输出滤波电容保持不变,则电感两端呈现正电压L i 0U U U =-,由于i 0U U >所以,在该电压作用下输出滤波电感中电流L i 线性增长,知道1t 时刻,L i 达到最大值L1I 。
在S 导通期间,电感电流的增量及开关管的占空比D 分别为21000L()s 1s ()(1)t t U U Ui dt T t D T L L L-∆=-=-=-⎰ 其中1st D T =( 0D 1<<) (2-1) 在[]1s t t 区间,S 关断,由于电感的储能作用,L i 经二极管VD 继续流通,此时加在输出滤波电感上的电压L 0U U =-,呈现负值,电感中电流L i 线性衰减,直到s T 时刻,L i 达到最小值L2I 。
在S 截至期间,电感电流的减小量为s1000L()s 1s ()(1)T t U U Ui dt T t D T L L L-∆=--=-=-⎰ (2-2) 由于稳态工作下的电感电流L i 波形必然周期性重复,因此S 导通期间L i 的增量必然等于S 截至期间的减小量,即L(+)L(-)i i ∆=∆,所以i 00s s (1)U U UDT D T L L-=- (2-3) 整理得iU D U =(2-4) 由式(2-4)可知,输出电压与开关管的占空比D 成正比,所以通过改变开关管的占空比可以控制输出平均电压的大小。
由于占空比总是小于1,所以输出电压总是小于输入电压,故常称为降压式变换器。
改变占空比就可以改变输出电压值。
(2)电感电流断续模式当电感较小,负载电阻较大或s T 较大时,将出现电感电流已下降到0,但新的周期却尚未开始的情况。
如图为电流断续模式下Buck 电路的相关波形图 电流断续模式下电路波形在[]10t 区间,开关管S 处于导通状态,与电感电流连续模式下的工作情况相同,此时()L L1i I +∆=。
在1T 时刻,S 关断,电感中电流L i 线性衰减,直到dis t 时刻下降到0,即dis1000L()dis 1s ()-∆=--=-=∆⎰t t U U Ui dt t t DT L L L(2-5) 式中,dis 1s(),(1)t t D D D T -∆=∆<-且。
由于L()L()=i i +-∆∆得 0(1)i U DD D U D D=∆<-+∆ ,其中 (2-6) 此时,变换器输出电流0I 任等于电感电流平均值,即2i0L1dis i S S 011(1)22U D I I t U T Lf U =⨯=- (2-7)上式表明。
电感电流断续时0i U U 不仅与占空比D 有关,而且与负载电流0I 有关。
若00I =,则D 多大,输出电压0U 必等于输入电压i U 。
(3)电感电流临界连续模式在有关电流断续工作模式的数学关系中,首先需要推导的是电感电流连续与断续的临界条件,其推导过程如下。
降压型电路电感电流处于连续与断续的临界状态时,在每个开关周期开始和结束的时刻,电感电流正好为零,如图2-4所示。
图 降压型电路电流临界连续工作时的波形稳态条件下,由于电容C 的开关周期平均电流为零,因此电感电流L i 在一个开关周期内的平均值等于负载电流为oo U I R=(2-8) 而电感电流L i 的开关周期平均值可以按下式计算:SL L 0()T I i t dt =⎰ (2-9)0L I I ≥,即得到电感电流连续的临界条件。
这种计算方法需要导出()L I t 的表达式,还要计算定积分,比较繁琐。
我们采用一种简单的方法。
根据图2-4,电感电流在一个开关周期中的波形正好是一个三角形,它的高L I ∆,底边长为s T ,面积为I L S 12S I T =∆ (2-10) 在几何意义上,电感电流的开关周期平均值等于和该三角形同底的矩形的高,因此电感电流开关周期平均值等于三角形面积除以s T ,即L L 12I I =∆ (2-11) L I ∆的计算方法如下:电感电流在零时刻从零开始线性上升,在s DT 时刻达到L I ∆,上升的斜率为Li o di LU U dt=- (2-12) 有: i oL S U U I DT L-∆=(2-13)此时电感电流仍为连续,故有oiU D U = 将其代入式(2-13),有L o S 1DI U T L-∆=(2-14) 则可得电感电流开关平均值的表达式为L o S 12DI U T L-=(2-15) 电感电流连续的临界条件为 0L I I ≥ 将式(2-8)和式(2-9)带入上式有00s12U D U T R L-≥ (2-16) 整理得S 12L DRT -≥ (2-17) 这就是用于判断降压型电路电感电流连续与否的临界条件。
随后需要推导的是电感电流断续条件下输出与出入电压的比例。
首先设开关S 关断后电感的续流时间为s aT ,如图3-7所示,其中()01a D ≤≤-。
图 电感电流断续工作时的波形根据稳态条件下电感电压开关平均值为零的原理,有i o S o S ()U U DT U T α-= (2-18) 电感电流开关周期平均值为L L 1()2I I D α=∆+ (2-19) 而负载电流为oo U I R= (2-20) 稳态条件下,电容C 的开关周期平均电流为零,故电感电流开关周期平均值等于负载电流,即o L 1()2U I D Rα∆+= (2-21) 从式(2-18)中,解出α的表达式,与式(2-15)一起代入式(2-21)中得i o o i S o ()12U U U U DT D L U R-= (2-22)整理得2i i 2o o S 2()0U U L U U D T R--= (2-23) 令2S 2LK D T R=解方程,并略去负根,得o i U U =(2-24)值得注意的是,式(2-24)在电路工作在电感电流断续条件下成立,而电路工作在电感电流连续条件下不成立。
特别是,当电感电流处于临界连续状态时,S ()2L/RT =1-D /,代入式(2-17)得时0i U U D =。
从式(2-17)可以看出,电流断续时电压比与占空比D 和负载R 相关,也与电路参数L 和s T 有关。
主回路电感、电容参数整定3【】22【】33【】根据对二电平Buck 型直流变换器工作原理的分析以及电感电流连续和断续的临界条件的推导,可以计算出二电平Buck 型直流变换器滤波电感和滤波电容的参数。
稳态时,电感电流连续的临界条件为:o L I I ≥ (2-25)利用上节内容提到的三角形面积法我们得到电感电流的临界条件为:S 12L DRT -≥ 整理得s 12DL RT -≥(2-26) 在本次的设计中,给定工作电压i U 为40V ,输出电压0U 为20V ,负载电阻R 为50Ω,开关周期s f 为40kHz ,带入式2-26中得到电感电流临界值:s 3111500.00031H 244010D L RT -≥=⨯⨯=⨯ (2-27) 即当主电路电感大于0.31mH 时, 电路工作在电感电流连续工作模式,当主电路电感小于0.31mH 时,则为电感电流断续工作模式。
