图的搜索算法
第7章图的深度和广度优先搜索遍历算法
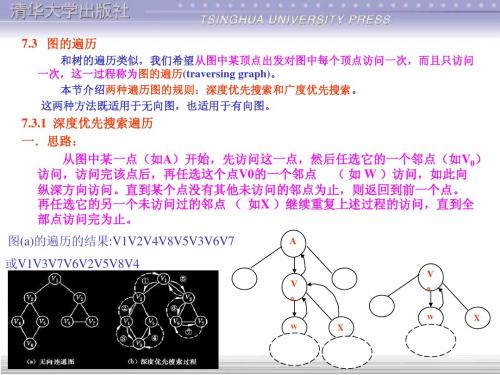
和树的遍历类似,我们希望从图中某顶点出发对图中每个顶点访问一次,而且只访问 一次,这一过程称为图的遍历(traversing graph)。 本节介绍两种遍历图的规则:深度优先搜索和广度优先搜索。 这两种方法既适用于无向图,也适用于有向图。
7.3.1 深度优先搜索遍历 一.思路: 从图中某一点(如A)开始,先访问这一点,然后任选它的一个邻点(如V0) 访问,访问完该点后,再任选这个点V0的一个邻点 ( 如 W )访问,如此向 纵深方向访问。直到某个点没有其他未访问的邻点为止,则返回到前一个点。 再任选它的另一个未访问过的邻点 ( 如X )继续重复上述过程的访问,直到全 部点访问完为止。 图(a)的遍历的结果:V1V2V4V8V5V3V6V7 或V1V3V7V6V2V5V8V4
p
v0 w x v 1
V
0
v 2
V
0
typedef struct {VEXNODE adjlist[MAXLEN]; // 邻接链表表头向量 int vexnum, arcnum; // 顶点数和边数 int kind; // 图的类型 }ADJGRAPH;
W W
X
X
7.3.2 广度优先搜索遍历 一.思路:
V
0
A V
0
W W
XXΒιβλιοθήκη 二.深度优先搜索算法的文字描述: 算法中设一数组visited,表示顶点是否访问过的标志。数组长度为 图的顶点数,初值均置为0,表示顶点均未被访问,当Vi被访问过,即 将visitsd对应分量置为1。将该数组设为全局变量。 { 确定从G中某一顶点V0出发,访问V0; visited[V0] = 1; 找出G中V0的第一个邻接顶点->w; while (w存在) do { if visited[w] == 0 继续进行深度优先搜索; 找出G中V0的下一个邻接顶点->w;} }
深度优先算法和广度优先算法的时间复杂度

深度优先算法和广度优先算法都是图搜索中常见的算法,它们具有不同的特点和适用场景。
在进行全面评估之前,让我们先来了解一下深度优先算法和广度优先算法的基本概念和原理。
### 1. 深度优先算法(Depth-First Search, DFS)深度优先算法是一种用于遍历或搜索树或图的算法。
其核心思想是从起始顶点出发,沿着一条路径直到末端,然后回溯,继续搜索下一条路径,直到所有路径都被探索。
在实际应用中,深度优先算法常常通过递归或栈来实现。
### 2. 广度优先算法(Breadth-First Search, BFS)广度优先算法也是一种用于遍历或搜索树或图的算法。
其核心思想是从起始顶点出发,依次遍历该顶点的所有相邻顶点,然后再以这些相邻顶点作为起点,继续遍历它们的相邻顶点,以此类推,直到所有顶点都被遍历。
在实际应用中,广度优先算法通常通过队列来实现。
### 3. 深度优先算法和广度优先算法的时间复杂度在实际应用中,我们经常需要对算法的时间复杂度进行分析。
针对深度优先算法和广度优先算法,它们的时间复杂度并不相同。
- 深度优先算法的时间复杂度:O(V + E),其中V为顶点数,E为边数。
在最坏的情况下,如果采用邻接矩阵来表示图的话,深度优先算法的时间复杂度为O(V^2);如果采用邻接表来表示图的话,时间复杂度为O(V + E)。
- 广度优先算法的时间复杂度:O(V + E),其中V为顶点数,E为边数。
无论采用邻接矩阵还是邻接表表示图,广度优先算法的时间复杂度都是O(V + E)。
### 4. 个人理解和观点在实际应用中,我们在选择使用深度优先算法还是广度优先算法时,需要根据具体的问题场景来进行选择。
如果要寻找图中的一条路径,或者判断两个节点之间是否存在路径,通常会选择使用深度优先算法;如果要寻找最短路径或者进行层次遍历,通常会选择使用广度优先算法。
深度优先算法和广度优先算法都是非常重要的图搜索算法,它们各自适用于不同的场景,并且具有不同的时间复杂度。
dfs和bfs算法

dfs和bfs算法深度优先搜索(DFS)和广度优先搜索(BFS)是图论中常用的两种搜索算法,也是许多算法题中的基础算法。
本文将从什么是图、什么是搜索算法开始介绍DFS、BFS的基本原理以及应用场景。
一、图的概念图是由节点集合以及它们之间连线所组成的数据结构。
图分为有向图和无向图两种,有向图中的边具有一定的方向性,而无向图中的边是没有方向的。
二、DFS(深度优先搜索)深度优先搜索从一个点开始,根据规定的遍历方式始终向着深度方向搜索下去,直到到达目标节点或者无法继续搜索为止。
具体实现可以用递归或者非递归的方式进行。
1、深度优先搜索的框架def dfs(v,visited,graph):visited[v] = True #将节点v标记为已经被访问#遍历v的所有连接节点for w in graph[v]:if not visited[w]:dfs(w,visited,graph)2、深度优先搜索的应用DFS常用来解决最长路径问题、拓扑排序问题以及判断图是否存在环。
三、BFS(广度优先搜索)广度优先搜索是从一个点开始,逐层扩散的搜索方式。
具体实现可以用队列实现。
1、广度优先搜索的框架def bfs(start,graph):visited = [False] * len(graph) #标记所有节点为未访问queue = [start] #队列存储已经访问过的节点visited[start] = True #起始点被标记为已经访问过while queue:v = queue.pop(0) #弹出队列首节点#遍历该节点的所有连接节点for w in graph[v]:if not visited[w]:visited[w] = True #标记该节点已经被访问queue.append(w) #加入队列2、广度优先搜索的应用BFS常用来解决最短路径问题,如迷宫问题、网络路由问题等。
四、DFS和BFS的区别DFS从一个节点开始,向下深度优先搜索,不断往下搜索直到无路可走才返回,因此将搜索过的节点用栈来存储。
dfs通用步骤-概述说明以及解释

dfs通用步骤-概述说明以及解释1.引言1.1 概述DFS(深度优先搜索)是一种常用的图遍历算法,它通过深度优先的策略来遍历图中的所有节点。
在DFS中,从起始节点开始,一直向下访问直到无法继续为止,然后返回到上一个未完成的节点,继续访问它的下一个未被访问的邻居节点。
这个过程不断重复,直到图中所有的节点都被访问为止。
DFS算法的核心思想是沿着一条路径尽可能深入地搜索,直到无法继续为止。
在搜索过程中,DFS会使用一个栈来保存待访问的节点,以及记录已经访问过的节点。
当访问一个节点时,将其标记为已访问,并将其所有未访问的邻居节点加入到栈中。
然后从栈中取出下一个节点进行访问,重复这个过程直到栈为空。
优点是DFS算法实现起来比较简单,而且在解决一些问题时具有较好的效果。
同时,DFS算法可以用来解决一些经典的问题,比如寻找图中的连通分量、判断图中是否存在环、图的拓扑排序等。
然而,DFS算法也存在一些缺点。
首先,DFS算法不保证找到最优解,有可能陷入局部最优解而无法找到全局最优解。
另外,如果图非常庞大且存在大量的无效节点,DFS可能会陷入无限循环或者无法找到解。
综上所述,DFS是一种常用的图遍历算法,可以用来解决一些问题,但需要注意其局限性和缺点。
在实际应用中,我们需要根据具体问题的特点来选择合适的搜索策略。
在下一部分中,我们将详细介绍DFS算法的通用步骤和要点,以便读者更好地理解和应用该算法。
1.2 文章结构文章结构部分的内容如下所示:文章结构:在本文中,将按照以下顺序介绍DFS(深度优先搜索)通用步骤。
首先,引言部分将概述DFS的基本概念和应用场景。
其次,正文部分将详细解释DFS通用步骤的两个要点。
最后,结论部分将总结本文的主要内容并展望未来DFS的发展趋势。
通过这样的结构安排,读者可以清晰地了解到DFS算法的基本原理和它在实际问题中的应用。
接下来,让我们开始正文的介绍。
1.3 目的目的部分的内容可以包括对DFS(Depth First Search,深度优先搜索)的应用和重要性进行介绍。
深度优先搜索算法

深度优先搜索算法(DFS)是一种常用的图算法,该算法主要用于解决有解路径或遍历某个图结构的问题。
的主要思路是从某个图的起始点出发,访问邻居节点,直到该节点没有未被访问的邻居节点为止,然后回溯到上一个节点继续遍历其他未被访问的邻居节点。
该算法的基本流程可以概括为以下几个步骤:1. 从某个图结构的起始点开始进行深度优先搜索。
2. 如果该节点没有未被访问的邻居节点,则回溯到上一个节点。
3. 继续遍历其他未被访问的邻居节点,直到所有的节点已被访问。
4. 搜索结束。
的实现可以使用递归或栈数据结构进行。
使用递归实现时,程序会自动保存每个节点的访问状态,无需手动进行处理。
使用栈数据结构实现时,需要手动保存每个节点的访问状态,以便在回溯时继续遍历其他未被访问的邻居节点。
主要应用于解决以下问题:1. 找出两点之间的最短路径可以用来查找两个节点之间的最短路径。
在进行深度优先搜索时,需要记录每个节点的前驱节点,以便在搜索结束后构造最短路径。
2. 遍历一张图结构可以用来遍历一张图结构。
在进行深度优先搜索时,可以将图中的所有节点都进行遍历。
3. 解决迷宫问题可以用来解决迷宫问题。
在进行深度优先搜索时,需要记录每个走过的位置,以便在搜索结束后构造出从起点到终点的路径。
4. 生成所有排列或组合可以用来生成所有排列或组合。
在进行深度优先搜索时,需要记录已经访问过的节点,以便在搜索结束后生成所有满足条件的排列或组合。
存在一些问题,例如搜索过程中容易陷入死循环、需要记录每个节点的访问状态等。
为了解决这些问题,可以使用剪枝、双向搜索等技术来优化搜索算法。
总之,是一种常用的图算法,该算法主要用于解决有解路径或遍历某个图结构的问题。
的主要思路是从某个图的起始点出发, 访问邻居节点,直到该节点没有未被访问的邻居节点为止,然后回溯到上一个节点继续遍历其他未被访问的邻居节点。
在实际应用中,可以用来查找两个节点之间的最短路径、遍历一张图结构、解决迷宫问题、生成所有排列或组合等。
第一讲 图的搜索算法

算法框架
1.算法的基本思路 算法设计的基本步骤为:
1)确定图的存储方式; 2)图的遍历过程中的操作,其中包括为输 出问题解而进行的存储操作;
3)输出问题的结论。
dfs与bfs 深度搜索与广度搜索的相近,最终都要扩展 一个结点的所有子结点. 区别在于对扩展结点过程,深度搜索扩 展的是E-结点的邻接结点中的一个,并将其 作为新的E-结点继续扩展,当前E-结点仍为 活结点,待搜索完其子结点后,回溯到该结 点扩展它的其它未搜索的邻接结点。而广度 搜索,则是扩展E-结点的所有邻接结点,E结点就成为一个死结点。
或改造,加入了一定的“智能因素”,使搜索能尽快接近目标结点,减少了在空间和 时间上的复杂度。 )
二、分支定界 三、A*算法 第三部分 搜索与动态规划的结合 (包括与其他算法的联系和对比)
初级的图搜索算法
• 包括 深度优先遍历,广度优先遍历和双向广度优先遍历 • 图的两种遍历算法:深度优先搜索和广度优先搜索算法 • BFS是一种盲目搜寻法,目的是系统地展开并检查图中 的所有节点,以找寻结果。换句话说,它并不考虑结果 的可能位址,彻底地搜索整张图,直到找到结果为止。 BFS并不使用经验法则算法。
广度优先搜索的应用
【例1】已知若干个城市的地图,求从一个 城市到另一个城市的路径,要求路径中经过的 城市最少 【例2】走迷宫问题
·
【例1】已知若干个城市的地图,求从一个城市到 另一个城市的路径,要求路径中经过的城市最少。
算法设计:
图的广度优先搜索类似与树的层次遍 历,逐层搜索正好可以尽快找到一个结点 与另一个结点相对而言最直接的路径。
如图5-6表示的是从城市A到城市H的交通图。从图中可 以看出,从城市A到城市H要经过若干个城市。现要找出一条 经过城市最少一条路线。 (提示:看到这图很容易想到用邻接距阵来表示,0
图的遍历和搜索

INPUT.TXT 123456789 3 OUTPUT.TXT 192 384 576 219 438 657 273 546 819 327 654 981
用数组B[0..9]来存储N个数字 存储规则: B[0]存储N个数字中0的个数 B[1]存储N个数字中1的个数 B[2]存储N个数字中2的个数 ………… ………… B[8]存储N个数字中8的个数 B[9]存储N个数字中9的个数
2 1
1 2
设置8个方向变化 初始化board Board[1,1] try(1,1,2,q) q 1
Y
N
输出结果
输出无解信息
K Try(x,y,i,q)
表示对(x,y)位置 作为第i步向前试探 的过程.若试探成 功,逻辑变量q的值 为true,否则为false
0 k←k+1 q1←false u←x+a[1,k] v←y+a[2,k] 合格 Y N Board=0 N Y Board[u,v] ←i i<n*n N
1 3 7 9 0 8 2 6 4 5
For I:=1 to 3 For j:=4 to 9 For k:=11 to 31 For p:=32 to 99
求I*i ,分离各位数字 求j*j ,分离各位数字 求k*k, 分离各位数字 求p*p , 分离各位数字
Y Try(u,v,i+1,q1) Q1:=true Not (q1) N Y Board[u,v]:=0 Q1 OR (K=8) Q:=Q1
试编程将1至N(N≤10)的自然数序列1,2,…, N重新排列,使任意相邻两数之和为素数.例如N =3时有两种排列方案123,321满足要求. 输入要求:N从键盘输入. 输出要求:每行输出一种排列方案(相邻数字之间 用空格分隔). 最后一行输出排列方案总数. 例如输入 3 输出 1 2 3 3 2 1 2
人工智能中图搜索算法(PDF 159页)

图4—5 八数码问题的广度优先搜索
第9页
第4章 图搜索技术
以上两个问题都是在某个有向图中寻找目标或路径问 题,这种问题图搜索问题。把描述问题的有向图称为状态 空间图,简称状态图。图中的节点代表问题中的一种格局, 一般称为问题的一个状态,边表示两个状态之间的联系。 在状态图中,从初始节点到目标节点的一条路径或者所找 到的目标节点,就是问题的解(路径解)。
谓搜索,顾名思义,就是从初始节点出发,沿着与之相连 的边试探地前进,寻找目标节点的过程(也可以反向进行)。 搜索过程中经过的节点和边,按原图的连接关系,形成树 型的有向图,称为搜索树。搜索过程应当随时记录搜索痕 迹。
1.搜索方式 用计算机来实现状态图的搜索,有两种最基本的方式: 树式搜索和线式搜索。 所谓树式搜索,形象地讲就是以“画树”的方式进行 搜索。 即从树根(初始节点)出发一笔一笔地描出来的。
状态图实际上是一类问题的抽象表示。事实上,有许
多智力问题(如梵塔问题、旅行商问题、八皇后问题、农
夫过河问题等)和实际问题(如路径规划、定理证明、演
绎推理、机器人行动规划等)都可以归结为在某一状态图
中寻找目标或路径的问题。因此,研究状态图搜索具有普
遍意义。
第10页
第4章 图搜索技术
4.1.2 状态图搜索 在状态图中寻找目标或路径的基本方法就是搜索。所
第4章 图搜索技术
3. 搜索算法 由于搜索的目的是为了寻找初始节点到目标节点 的路径,所以在搜索过程中就得随时记录搜索轨迹。 为此,我们用一个称为CLOSED表的动态数据结构来 专门记录考查过的节点。显然,对于树式搜索来说, CLOSED表中存储的正是一棵不断成长的搜索树;而 对于线式搜索来说,CLOSED表中存储的是一条不断 伸长的折线,它可能本身就是所求的路径(如果能找到 目标节点的话)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
问题的理解与描述
• 一个有向无圈图G = <V, E>(DAG)的拓扑排序 是其所有顶点的一个线性排列,使得若边(u, v) 包含在G中,则u在排列中必出现在v前(若图 不是无圈的,则不可能有此线性排列)。一个 图的拓扑排序可被视为将图的所有顶点水平排 列时,所有的有向边从左指向右。 • 输入:有向图G。 • 输出:若G是DAG,输出G的各顶点的一个拓扑 排序,否则输出出错信息。
算法伪代码描述
• • • • • • • • • • • • • • • • • • • • • • • TOPLOGICAL-SORT(G) 1 for each vertex uV[G] 2 do color[u]←WHITE 3 acyclicity←true 4 top-logic←S← 5 for each vertex s V[G] 6 do if color[s] = WHITE 7 then color[s] ← GRAY 8 PUSH(S, s) 9 while S≠ 10 do u←TOP(S) 11 if v Adj[u] and color[v] = GRAY 12 then acyclicity←false 13 if v Adj[u] and color[v] = WHITE 14 then color[v] ←GRAY 15 PUSH(S, v) 16 else color[u] ← BLACK 17 PUSH(top-logic, u) 18 POP(S) 19 if acyclicity=true 20 then return top-logic 21 else print "G is not a DAG!“ 由于TOPLOGICAL-SORT的运行时间与DFS的运行时间一致,所以,可以在时间Θ(V + E)内计算有向无圈图G=<V, E>的拓 扑排序。
DFS图例
1/ (a) b a e (b) 2/ b 1/ a e b S a (c) 2/ b 1/ 3/ f c 1/ e 5/ d a 3/ f c 1/ 8/9 e 5/6 d b S a 2/11 b (k) 4/7 a 8/9 e 5/6 d (l) 2/11 b 4/7 5/6 d 8/ e 2/ e S f b a (i) b 4/7 d S (f) c f b a 2/ b 4/ 3/ f c 1/ 3/ f c 1/12 a 3/10 f c 8/9 e 5/6 d a 8/9 e 5/6 d f S b a 5/6 d a e d a e f b a S f c 1/ (d) 2/ b 4/ 3/ f c 1/ (g) 2/ b 4/7 3/ f c 1/ (j) 2/ b 4/7 a 5/6 d a e f S b a (h) 2/ b 4/7 d a e (e) 2/ b 4/ d f c 1/ 3/ f c 1/ a d a S
• DFS算法可以修改成能对各条边在遇到它们时进行分类。关键的思想 是,每一条边(u, v)在首次被探索时可以根据顶点v的颜色来分类(但 是进边和跨边不能区分): • 白色(WHITE)意味着一条树枝边; • 灰色(GRAY)意味着一条回边; • 黑色(BLACK)意味着一条进边或跨边。
• 图G是无圈的充分必要条件是G的一次深度优先搜索不产生回边。
问题的理解与描述
• 在深度优先搜索过程中对每一个顶点u跟踪 两个时间:发现时间d[u]和完成时间f [u]。 d[u]记录首次发现(u由白色变成灰色)时 刻,f [u]记录完成v的邻接表检测(变成黑 色)时刻。 • 输入:图G=<V, E>。 • 输出:G的深度优先森林G以及图中各顶点 在搜索过程中的发现时间和完成时间。
c S f b a
c S f b a3Biblioteka 10 f c3/10 f c
a S
S
算法的运行时间
• DFS的运行时间如何?第1~2行的循环Θ(V)。 内嵌于第14~20行操作对G的每条边执行一 次,因此耗时
vV
| Adj[v] | O( E )
• 所以DFS的运行时间为Θ(V + E)。
有向无圈图的拓扑排序
图的邻接表
邻接表对算法效率的影响
• • • • • • TRANSPOSE-DIRECTED-GRAPH(G) 1 for u←1 to |V| do 2 for v←1 to |V| do 3 AT[v, u] ←A[u, v] 4 return GT 运行为时间(|V|2)。 • • • • • • • • TRANSPOSE-DIRECTED-GRAPH(G) 1 for each uV do 2 AdjT[u]←NIL 3 for each uV do 4 for each v Adj[u] do 5 INSERT(AdjT[v], u) 6 return GT 运行为时间(|V|+|E|)。
10.1 深度优先搜索
• 深度优先搜索(Depth First Search,DFS)所遵循 的策略,如同其名称所说,是在图中尽可能“更 深”地进行搜索。在深度优先搜索中,对最新发 现的顶点v若此顶点尚有未探索过从其出发的边就 探索之。当v的所有边都被探索过,搜索“回溯” 到从其出发发现顶点v的顶点。此过程继续直至发 现所有从源点可达的顶点。若图中还有未发现的 顶点,则以其中之一为新的源点重复搜索,直至 所有的顶点都被发现。与BFS中源顶点是指定的稍 有不同。 DFS搜索轨迹G将形成一片森林—— 深 度优先森林
算法伪代码描述
• • • • • • • • • • • • • • • • • • • • • • DFS(G) 1 for each vertex uV[G] 2 do color[u]←WHITE 3 [u] ←NIL 4 time← 0 5 S ← 6 for each vertex s V[G] 7 do if color[s] = WHITE 8 then color[s] ← GRAY 9 d[s] ← time← time +1 10 PUSH(S, s) 11 while S≠ 12 do u←TOP(S) 13 if v Adj[u] and color[v] = WHITE 14 then color[v] ←GRAY 15 [v] ←u 16 d[v] ← time← time +1 17 PUSH(S, v) 18 else color[u] ← BLACK 19 f [u] ← time ← time +1 20 POP(S) 21 return d, f, and
